正交各向异性路基路面在移动荷载作用下的空间动力响应

王 博， 张春丽,2， 祝彦知

(1.郑州大学 水利与环境学院，河南 郑州 450001； 2.中原工学院 信息商务学院，河南 郑州 450007； 3.中原工学院 建筑工程学院，河南 郑州 450007)

0 引言

在实际工程中，移动荷载并非直接作用在地基表面，而是通过路面将荷载分布到地基表面．路基路面动力学问题一直受到国内外学者的关注,文献[1-3]用解析法、文献[4-5]利用半解析方法、文献[6]利用模型试验与数值仿真方法、文献[7]利用有限元软件研究了路基路面动力响应问题．文献[8]通过现场测试揭示了行车荷载下沥青路面和地基的动力影响规律．文献[9]研究了横观各向同性地基上无限板的稳态振动，并用数值结果表明，采用各向同性介质的动力学模型，不能准确描述具有明显各向异性特性地基的动力性能，需要建立更符合实际情况的各向异性地基模型来研究移动荷载作用下路基路面的动力响应．文献[10-12]研究了正交各向异性地基及覆无限大板的平面应变问题的动力响应．对移动荷载作用下地基板的动力响应问题，目前研究工作主要集中在对各向同性或横观各向同性地基的动力研究，以及正交各向异性地基平面应变问题研究，但动荷载作用下正交各向异性无限大板的空间动力响应鲜见报道．

笔者建立正交各向异性弹性地基上覆无限大弹性板的路基路面三维空间力学模型，研究在车辆荷载作用下板和地基的动力响应．对移动矩形谐振荷载作用下公路路面板动力稳态问题进行了算例分析，研究了土体参数对板位移的影响规律．

1 直角坐标系下的振动方程

1.1 力学模型

车辆移动荷载函数一般能通过傅里叶级数展开为若干个简谐荷载之和.笔者把车辆荷载简化为匀速移动均布矩形简谐荷载，用Kirchhoff小变形无限大弹性薄板来模拟路面，用弹性半空间来模拟路面以下的土体．

假设薄板受横向荷载q(x1,y1,t)=

以速度c沿x1轴正向移动，则在板底必有地基反力p(x1,y1,t)，根据作用力与反作用力定律，在地基表面同样有作用力p(x1,y1,t)，且方向相反，如图1所示．

1.2 坐标变换

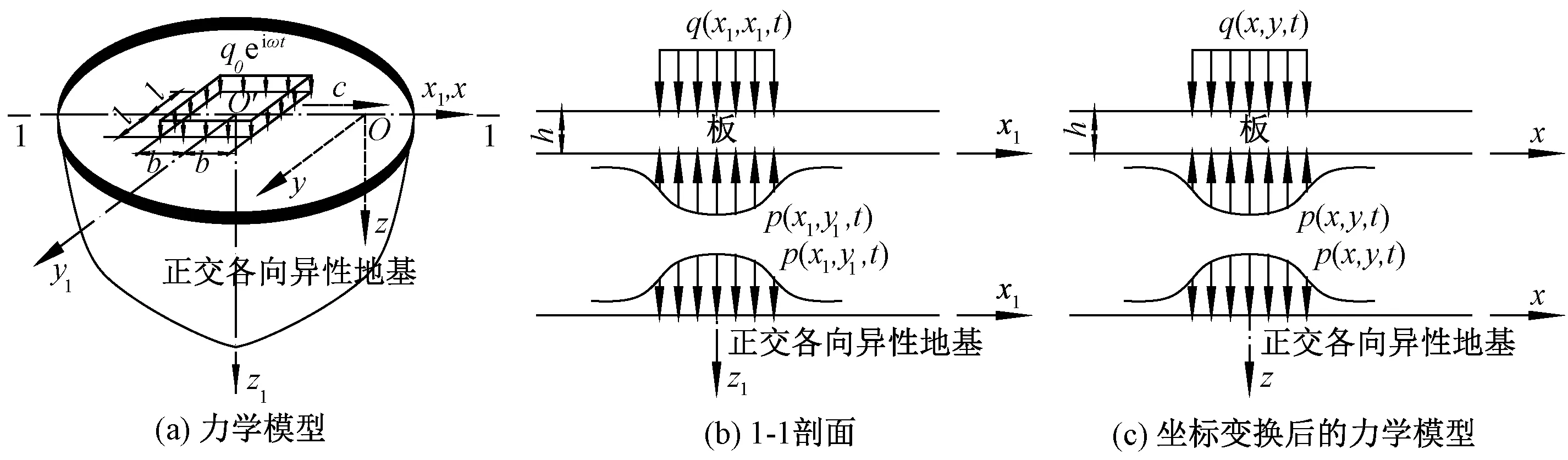
图1 半空间上覆无限大弹性板的力学模型Fig.1 Mechanics model of elastic plate on half space

(1)

各变量在移动坐标系下可以表述为：

Ψ(x1-ct,y1,z1,t)=Ψ(x,y,z)eiωt;

(2a)

(2b)

(2c)

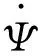
1.3 基本方程

笔者仅分析稳态动力响应问题，弹性地基上弹性地基板在动力荷载作用下的运动微分方程:

(3)

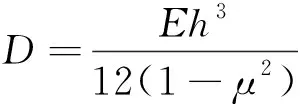
对于正交各向异性弹性地基上作用动荷载的空间问题，有方程:

(4)

(5a)

(5b)

(5c)

(5d)

(5e)

(5f)

式中：ux、uy、uz分别表示沿移动坐标系x、y、z方向的位移；σx、σy、σz、τyz、τzx、τxy为土体应力分量；c11、c12、c13、c22、c23、c33、c44、c55、c66为正交各向异性地基的9个相互独立的弹性常数．

2 振动方程的求解

2.1 边界条件

弹性地基半空间表面边界条件为：

(6a)

(6b)

对于简谐荷载，所有分量均有因子eiωt，因此为了书写方便，在求解时先略去因子eiωt．当板置于地基上并与之共同工作时，板底面与地基表面的垂直位移相同，同时板与地基光滑接触[13],则有应力和变形协调边界条件：

σz(x,y,0,t)=-p(x,y)；

(6c)

τzx(x,y,0,t)=0；

(6d)

τyz(x,y,0,t)=0；

(6e)

uz(x,y,0,t)=w(x,y,t).

(6f)

2.2 求解方程

对坐标x、y的Fourier变换定义如下：

(7a)

相应的逆变换为：

(7b)

式中：ξ、η为Fourier变换参数．

对板的动力方程式(3)做关于x、y的Fourier变换，得到

(8)

式中：L=D(ξ2+η2)2+m(-c2ξ2+2ωcξ-ω2)．

对弹性半空间体的动力方程式(4)同样做Fourier变换，并改写成矩阵形式:

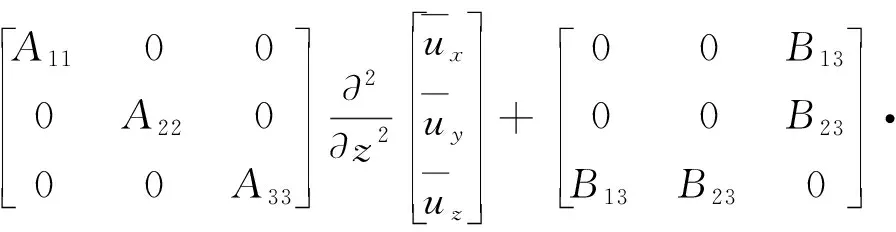
(9)

式中：A11=-c55；A22=-c44；A33=-c33；B13=-iξ(c13+c55)；B23=-iη(c23+c44)；D11=c11ξ2+c66η2+ρ(-c2ξ2+2ωξc-ω2)；D12=ξη(c12+c66)；D22=c66ξ2+c22η2+ρ(-c2ξ2+2ωξc-ω2)；D33=c55ξ2+c44η2+ρ(-c2ξ2+2ωξc-ω2)．

设方程(9)的解为：

(10)

把式(10)带入方程(9)得特征方程：

a1λ6+a2λ4+a3λ2+a4=0，

(11)

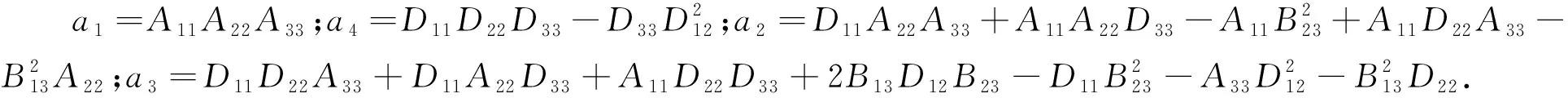
特征方程(11)为复系数一元六次方程，其根为±λ1,±λ2,±λ3，(Re[λj]≥0,j=1,2,3)，可表示为:

(12a)

(12b)

(12c)

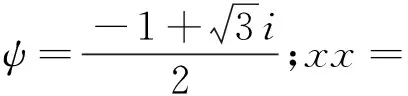
对于z≥0的正交各向异性半空间的动力分析问题，当z→∞时，ux、uy、uz均应趋于零,则矩阵方程(9)的解为：

(13a)

(13b)

(13c)

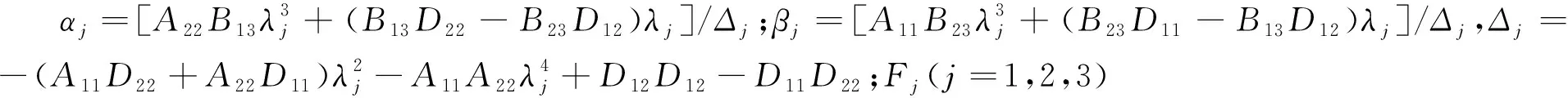
利用应力、应变和位移之间的关系，可以得到应力变量的表达式：

(13d)

(13e)

对边界条件式(6c)～(6f)做关于x、y的Fourier变换,可以求得：

(14a)

(14b)

(14c)

(14d)

将式(14a)～(14c)代入式(13d)～(13e)，并令线性方程组系数为：

(15)

则待定系数Fj(j=1、2、3)为:

(16)

式中：Δ=p3q2r1+p1q3r2+p2q1r3-p2q3r1-p3q1r2-p1q2r3．

将式(16)代入式(13c),得到地基的竖向位移为:

(q2r1-q1r2)e-λ3z].

(17)

将式(8)和式(17)带入位移边界条件(14d)，推出地基反力即接触应力的大小为：

(18)

板挠度为：

(19)

对薄板作用的横向荷载做关于x、y的Fourier变换，可以求得：

(20)

对式(13)、(18)、(19)、(20)施加关于x和y的Fourier逆变换，就可以得到移动谐振荷载作用下正交各向异性介质在直角坐标系下响应的积分形式解．由于文章篇幅有限，仅给出板位移的积分表达式：

(21)

3 算例分析

算例模型如图1所示，给出移动谐振荷载作用下某公路路面板位移影响数值结果．作用在板上的荷载半长度b=0.075 m，l=0.075 m，峰值q0=100 kPa，荷载频率f=16 Hz，移动速度c=35 m/s．板弹性模量3.0×1010Pa，泊松比0.15，板厚0.25 m，密度2 400 kg/m3．土体弹性参数Ex=50 MPa，μxy=0.25，Gyz=20 MPa，Gzx=24 MPa，Gxy=15 MPa，ρ=1 815 kg/m3．引入描述土体正交各向异性参数之间的比例系数km(m=1、2、3、4)，令Ey=k1Ex，Ez=k2Ex，μxz=k3μxy，μyz=k4μxy．当km=1时，土体为各向同性．

μij本身变化不大，它对动力响应的影响可以忽略不计[13]，取k3=1.2，k4=1.6．弹性系数c11～c55和Ei、μij、Gij之间的关系见文献[14]．

图2和图3分别为k2=0.8，仅改变k1时的板位移沿x方向的波形图(y=0)和y方向的波形图(x=0),图4和图5分别给出k1=1.2，仅改变k2时的板位移在x方向的波形图(y=0)和在y方向的波形图(x=0),其中km=1对应的图形表示各向同性土体时的板变形．

图2 不同土体Ey时板位移在x方向的波形(y=0)Fig.2 Plate deformation curves in the direction of x due to different Ey(y=0)

图3 不同土体Ey时板位移在y方向的波形(x=0)Fig.3 Plate deformation curves in the direction of y due to different Ey(x=0)

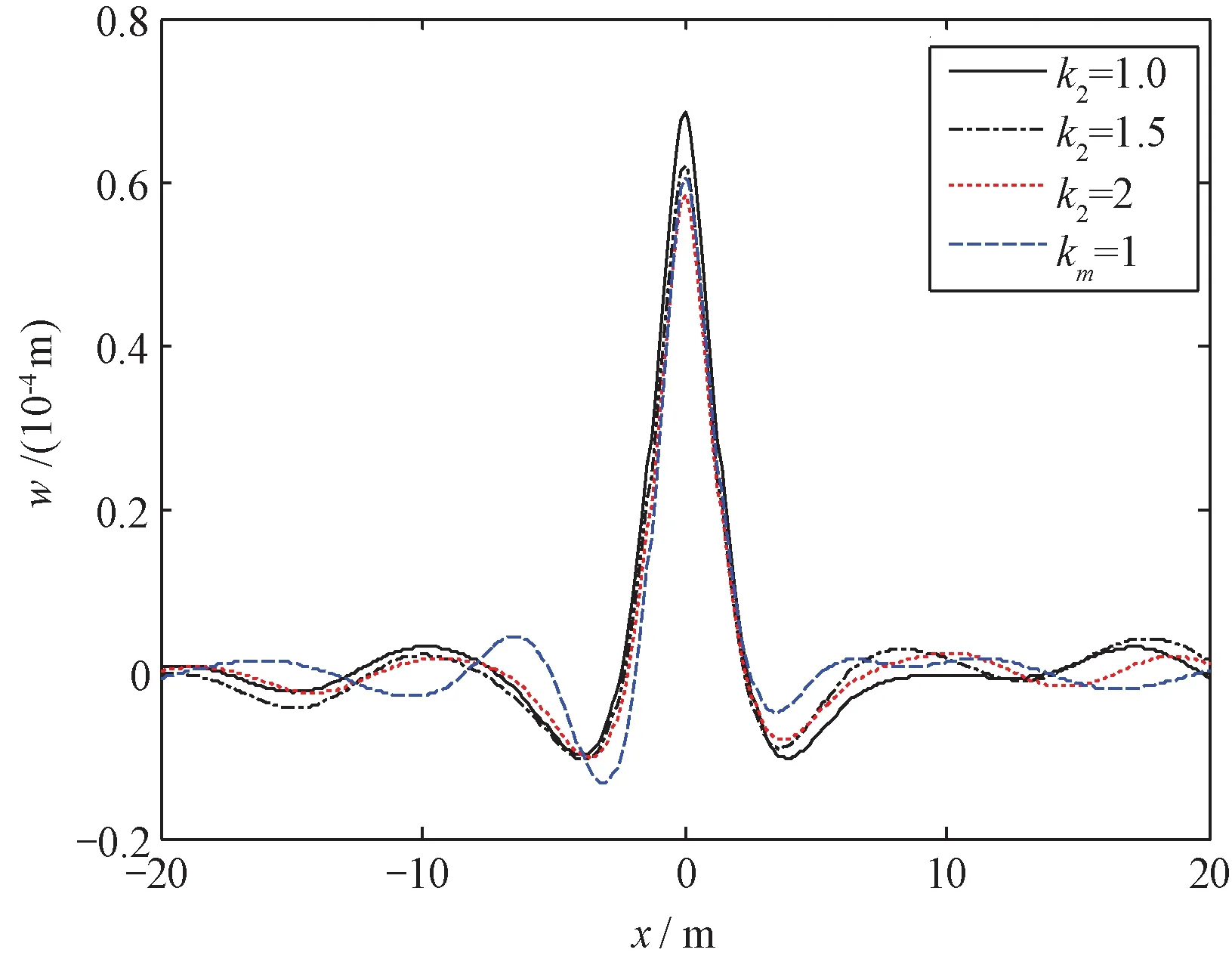
图4 不同土体Ez时板位移在x方向的波形(y=0)Fig.4 Plate deformation curves in the direction of x due to different Ez(y=0)

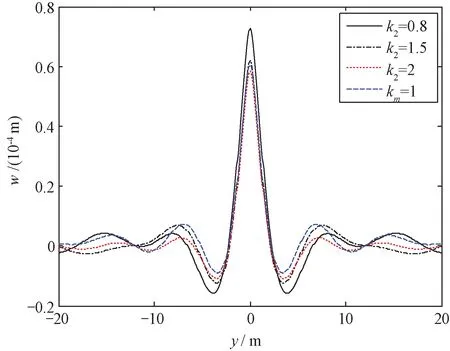
图5 不同土体Ez时板位移在y方向的波形(x=0)Fig.5 Plate deformation curves in the direction of y due to different Ez(x=0)

从图2～5可以看出,土体的各向异性对板沿x和y方向的位移都有较大影响.在x方向的波形中，负的最大位移均出现在荷载作用范围外的左侧，曲线不对称；在y方向的波形中，板位移曲线关于y=0对称.随着k1即Ey的增加，板位移最大值略有增加，各向同性时的最小，k1=1.2和k1=2时的曲线在离荷载作用中心点约2 m范围内非常接近.随着k2即Ez的增加，板位移的最大值却明显减小，各向同性时的值仅大于k2=2的值.离荷载中心点较远处的板位移曲线有明显的振动，但是振幅较小并趋于平缓，且在某些范围内有负值出现．如果板的变形过大，可以适当增加土体z向的弹性模量Ez，或者减小y向的弹性模量Ey．

4 结论

笔者研究了移动谐振荷载作用下正交各向异性地基上覆无限大板的空间动力响应问题，得到了动力响应的积分形式解．对移动谐振荷载作用下公路路面板动力稳态问题进行了算例分析并进行了参数分析，研究了土体参数对板位移影响规律．数值分析结果表明：(1)考虑土体的正交各向异性更能准确描述路基路面相互作用的动力响应；(2)Ey对板变形影响很小，而Ez对板变形的影响却很大，要综合考虑各种因素设计合适的地基弹性模量．