基于二阶锥规划的主动配电网动态无功优化

章 健， 熊壮壮， 王明东， 朱永胜

(1.郑州大学 产业技术研究院，河南 郑州 450001； 2.中原工学院 电子信息学院，河南 郑州 450007)

0 引言

随着分布式电源(distributed energy resources，DER)的渗透率不断提高，分布式电源的不确定性给传统配电网带来了诸多挑战，如接入点电压升高、系统双向潮流、短路电流升高、分布式电源的消纳等[1].由此主动配电网(active distribution network,ADN)概念应运而生，主动配电网是通过使用灵活的网络拓扑结构来管理潮流，以便对局部的DER进行主动控制和主动管理的配电系统[2].未来的配电网是同时含有多种主动管理装置的配电网，例如风电、光电、储能系统(energy storage system，ESS)、分组投切电容器组(capacitors banks，CB)、静止无功补偿器(static VAR compensation，SVC)、有载调压变压器(onload tap changer，OLTC)，如何制定这些主动管理装置的控制策略关系到主动配电网优化运行.

由于主动配电网优化运行的研究中含有很多离散变量和整数变量，以及配电网潮流等式的非凸，使得求解过程比较困难，属于非确定性多项式(non-deterministic polynomial)问题，当前许多智能算法如粒子群算法[3]、遗传算法[4]、进化算法[5]确实能求解这些非凸问题.但是，智能算法运用到主动配电网无功优化中，容易陷入局部最优解且求解速度很慢.文献[6]建立了以网损为目标的主动配电网随机无功优化模型，并用粒子群算法来求解，且只是将网损作为单目标；文献[7]建立了考虑网损、电压偏差的配电网随机无功优化模型，但其没有考虑储能系统.文献[8-9]考虑到集中调控的不可靠性，将配电网进行分区来进行无功优化，使用交替方向乘子法来进行求解,但考虑的无功控制装置仅仅只限于DG;文献[10-11]利用二阶锥规划(second order cone programming，SOCP)来求解无功优化问题，但目标函数仅仅为网损，比较单一.

针对以上问题，笔者考虑DG、ESS、CB、SVC、OLTC等主动管理装置，以弃风、弃光、网损、电压偏差为目标函数，建立了配电网多目标无功优化模型,然后利用层次分析法将多目标函数转化为单目标函数，通过对模型进行线性化处理和松弛凸化为二阶锥(SOCP)的形式，再用商业求解器Cplex来进行求解，从而制定出这些主动管理装置的动态投切策略.

1 主动配电网建模

1.1 主动管理装置的建模

1.1.1 储能装置建模

通常情况下储能装置具有削峰填谷、改善电压质量等作用.笔者主要考虑电量平衡限制、电量剩余限制、充电限制，忽略储能装置的电量随时间的损失，其模型为：

Ej,t+1=Ej,t+ηch,jPch,j,tΔt-Pdch,j,t/ηdch,jΔt,

(1)

Ej,max·20%≤Ej,t≤Ej,max·90%,

(2)

Mch,j,t+Mdch,j,t≤1,

(3)

(4)

式中：Ej,t为t时刻第j节点上所连接的电量；Pch,j,t、ηch,j、Pdch,j,t、ηdch,j分别为第j节点上连接储能装置的充电功率、充电效率、放电功率、放电效率;Δt为调度时间间隔；Ej,max为储能装置的最大容量；Mch,j,t、Mdch,j,t为0、1变量，保证充放电不能同时进行；Pch,j,max、Pdch,j,max分别为充放电的最大功率.式(1)为电量平衡限制；式(2)为了保证储能装置的寿命设定的电池剩余限制；式(3)为储能装置的充放电限制，保证储能装置在调度周期内的某一时刻只能处于充电、放电和不充电也不放电的3种状态中的一种；式(4)为充放电的功率限制.

1.1.2 无功装置建模

(1)连续的无功调节.

(5)

(2)离散的无功调节.离散的无功调节主要是分组投切电容器组.

(6)

(7)

(8)

(9)

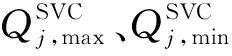
1.1.3 OLTC的建模

Ui,t=nij,tUj,t；

(10)

nij,t=nij,0+Kij,tΔnij；

(11)

-Kij,max≤Kij,t≤Kij,max；

(12)

(13)

(14)

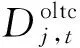
1.2 目标函数建模

笔者建立多目标模型，分别考虑网损、弃风和弃光和电压偏差.

(1)网损.

(15)

(2)弃风和弃光.

(16)

(3)电压偏差.笔者将电压限制在一定的区间范围内，如果越界，采取罚函数的形式进行惩罚，具体表达式为：

(17)

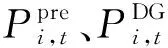
1.3 运行约束

1.3.1 功率平衡约束

目前在配电网优化控制策略制定中，配电网潮流形式一般采用Distflow支路潮流[10]形式.其实质就是流入节点的功率与流出节点的功率平衡.

(18)

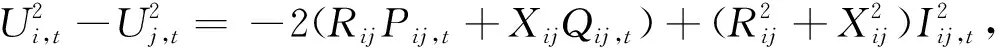
(19)

(20)

(21)

式中：φ(j)是辐射电网中以j为末端节点的支路首端节点集合；ψ(j)是以j为首端节点的支路的末端节点集合；Pij,t、Qij,t为i、j支路的首端t时刻的有功和无功功率；Ui,t、Uj,t和Iij,t为t时刻ij节点的电压幅值和i、j支路电流幅值；Rij、Xij为i、j支路的电阻和电抗.式(18)为有功平衡约束；式(20)是保证无功平衡；式(19)和(21)是电压降平衡约束.

1.3.2 电压及电流上下限约束

Uj,min≤Uj,t≤Uj,max;

(22)

0≤Iij,t≤Iij,max,

(23)

式中：Uj,min、Uj,max为电压的上下界；Iij,max为电流最大值.

1.3.3 变电站关口约束

主动配电网的功率波动会对输电网的电能质量造成影响，所以配变口交换功率应该控制在一定的范围内[10].

(24)

式中：P0，max、P0，min为变电站节点的输出功率的上下界，P0，t为从变电站节点流出的功率.

1.3.4 分布式电源约束

随着分布式电源的发展，现在越来越多的DG可以进行无功调节，对于DG无功方面的控制，有恒功率和变功率控制，笔者主要考虑恒功率的控制.θ为功率因素角.

(25)

2 模型的转化

2.1 二阶锥模型

由于所建模型是大规模非凸非线性的混合整数规划问题，现有的诸如智能算法容易陷入局部最优解，二阶锥规划算法能良好地解决这些问题.

二阶锥的标准形式[12]：

式中：变量x∈RN；系数常量b∈RM;c∈RN;AM×N∈RM×N；K为二阶锥或旋转二阶锥.

二阶锥：

}.

2.2 模型的锥化

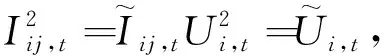
(26)

然后将式(26)化为(27).

(27)

对于目标函数fu不满足二阶锥规划的模型，必须对其进行处理：

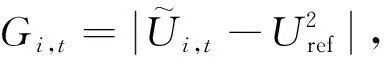
添加如下附加约束[13]:

(28)

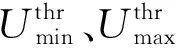
式(22)和(23)相应转化为：

(29)

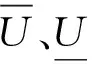
相应的式(10)变成：

(30)

由于式(11)的非线性，可以处理成如下形式[14]：

(32)

(33)

(34)

并添加如下约束：

(35)

(36)

因此,式(10)和(11)就线性化为(32)、(33)、(34)、(35)、(36).

2.3 目标函数的多目标处理

目前处理多目标模型的方法主要有：将多目标转化为单目标来求解、帕累托前沿[15]等方法.笔者通过对多目标进行加权转化为单目标进行求解.利用层次分析法(analytic hierarchy process, AHP)[16]来确定系数.

F=w1floss+w2fcur+w3fu.

根据层次分析法算出来权重:w1=0.625 0,w2=0.238 5,w3=0.136 5.

2.4 模型求解

经过上述线性化和锥化处理之后，潮流等式(18)～(20)也将变成线性式，如果不考虑整数变量，模型为二阶锥规划(SOCP)模型.本文由于含有离散变量，无功优化的模型变成了混合整数二阶锥规划模型(mixed integer second order cone programming，MISOCP)，一些商业软件能快速地求解这种模型，如Cplex、Gurobi、Mosek.

3 算例分析

3.1 测试环境与算例

为了验证笔者所建的模型的正确性和有效性，在Yalmip上建模，在MATLAB2016b平台上采用Cplex 12.7求解器进行求解.测试系统的硬件环境是英特尔Pentium(R)J2900，4 GB内存，64位windows 8操作系统.

笔者在修改的IEEE 33节点上进行仿真计算.图1为某地典型的分布式电源和负荷的日运行曲线，风机与光伏接入的位置如表1所示[16].ESS的容量为1 200 kVA,充放电功率为240 kW·h,效率为0.938 1.SVC接在节点25，补偿范围为-300～500 kvar，为了提高分布式电源的利用率，将渗透率分别设置为25%、50%、75%、100%，观察节点电压是否越界.分组投切电容器的基本参数如表2所示，电压基准值选择12.66 kV，电压的上下限是0.95～1.05，节点电压的优化区间为0.97～1.03.

3.2 结果分析

笔者分别就3种场景进行分析，情景1：无储能系统，考虑电压偏差；情景2：有储能系统，不考虑电压偏差；情景3：有储能系统，考虑电压偏差.分别在分布式电源渗透功率为25%、50%、75%、100%时，对上面3种情景进行算例分析，结果如表3所示.

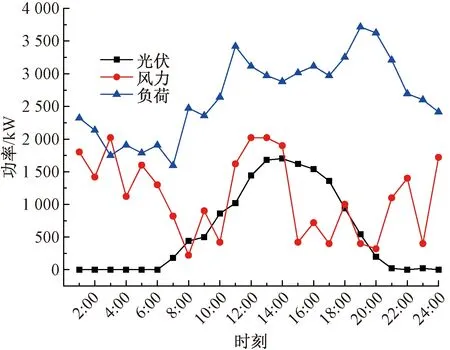
图1 分布式电源出力和负荷曲线Fig.1 Curve for load demand and DG output

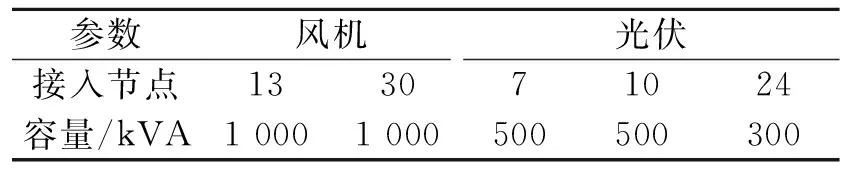
参数风机光伏接入节点13307102427容量/kVA1 0001 000500500300300

表2 CB的安装位置和参数Tab.2 Basic installation parameters of CB

从表3中通过B1和B3、C1和C3、D1和D3、E1和E3对比可以看到，储能装置作为有功参与优化的时候能降低网损和电压偏差.从B2和B3、C2和C3、E2和E3、D2和D3中可以看出，当不将电压偏差作为优化目标时，可以适当降低网损，但同时会造成较大的电压偏差，影响电压质量.随着渗透率的不断提高，分布式电源参与优化时，能改变配电网中的潮流，达到降低网损的目标，但是对弃风和弃光影响不是很大，这是因为笔者所建的储能系统模型只能进行有功调节，不能进行无功调节.

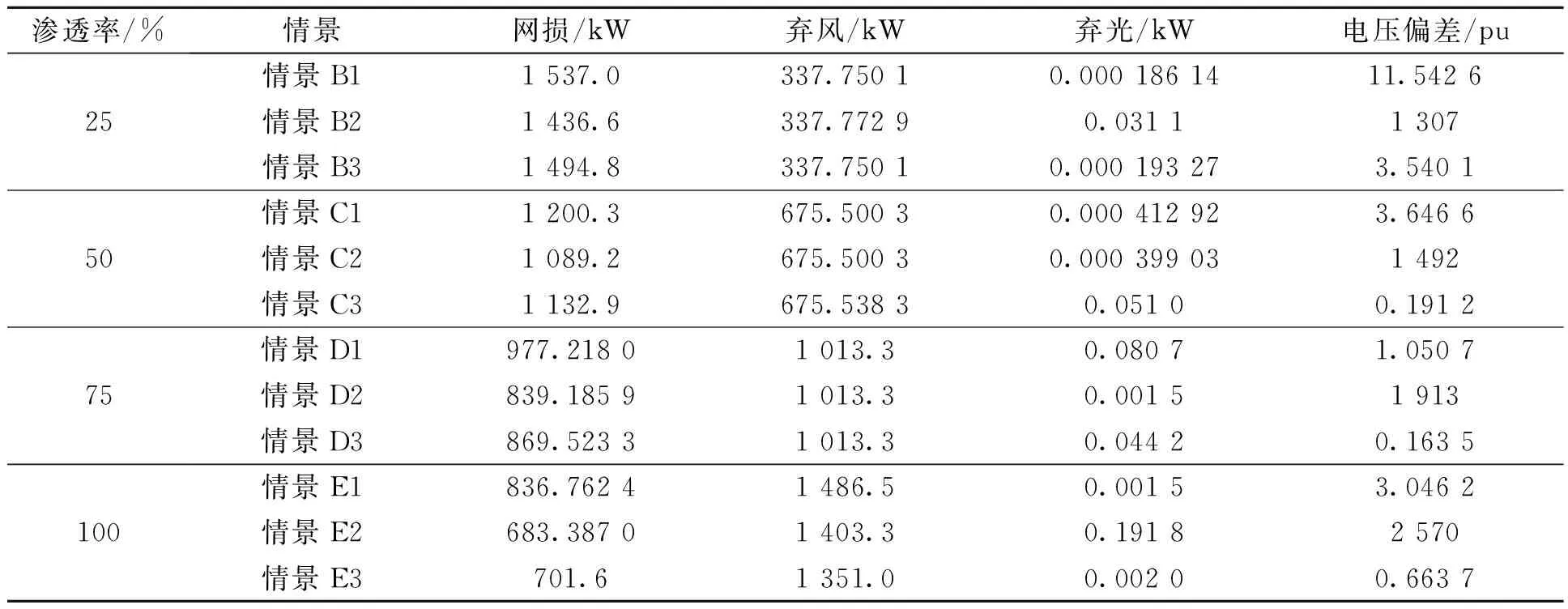
表3 不同情景下的网损及弃DG功率和电压偏差Tab.3 The network loss，abandon DG and voltage deviation under different scenarios

从图2可以看出，在渗透率达到100%时，情景E3时的电压偏差较小，而无储能装置作为有功协调优化时，电压明显偏高，不计及电压偏差时，电压偏差较大.在0：00的时候,由于负荷需求高于分布式电源的出力，导致电压相对较低，在4：00的时候，由于分布式电源出力增大，会抬高电压，在大概中午11：00的时候，由于负荷需求大，电压会下降，在14：00的时候，由于风电出力突然降低，会造成电压降低，在20：00的时候，由于负荷的持续增大，电压会降低到最低点，但是电压都没有越界，保持在较好的状态.

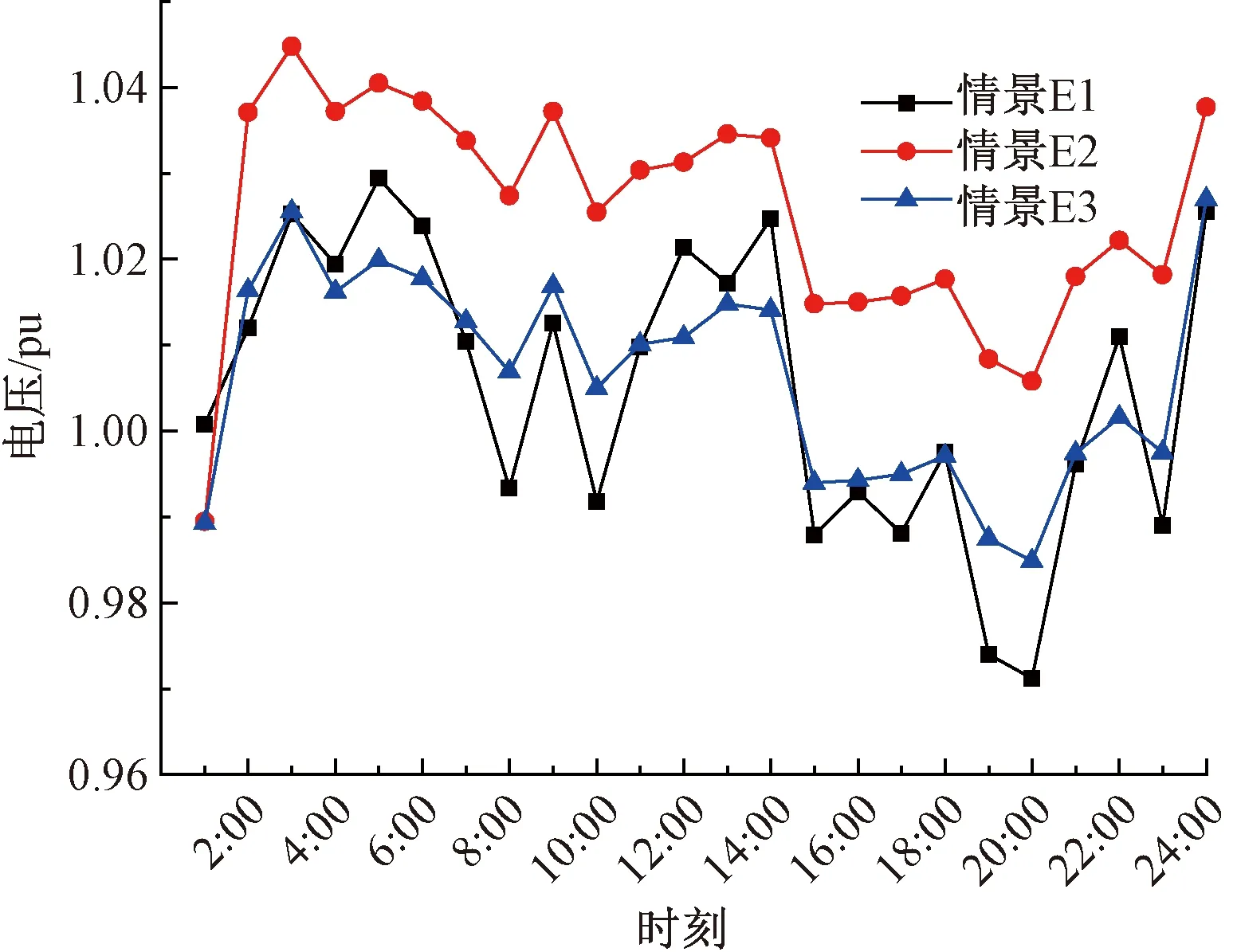
图2 33节点的电压Fig.2 Voltage value of 33 node

从图3中可以看出，当渗透率不断增大时，配电网中的电压也增大，但是在笔者所提出的控制策略下，电压没有越界，而是稳定在0.96～1.03 pu之间，充分证明所提出的控制策略的有效性.

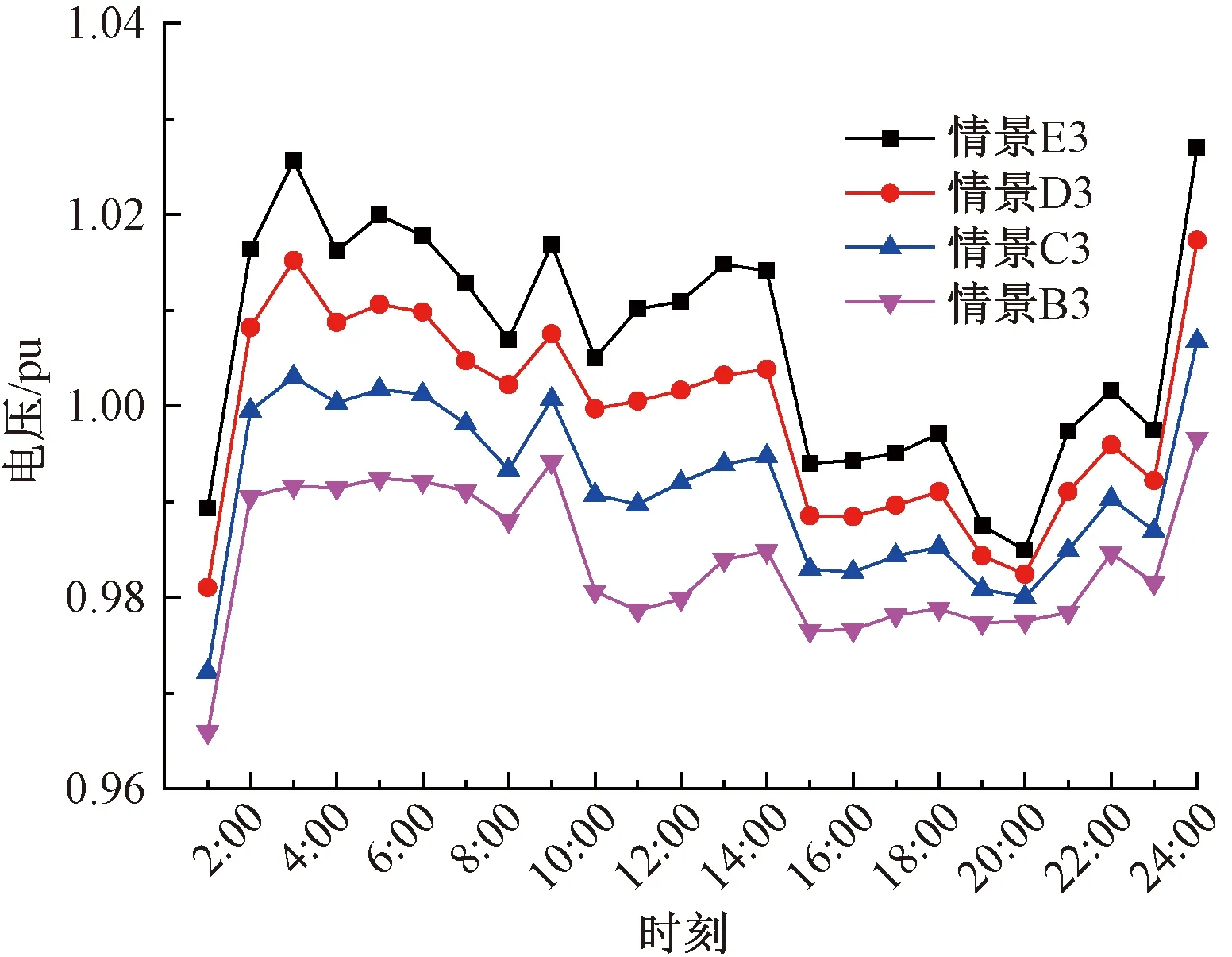
图3 渗透率不同时18节点的电压Fig.3 The voltage of 18 nodes with different permeability

图4和图5是渗透率为75%时的控制策略.图4是CB的控制策略；图5是ESS控制策略.从图4可以看出，储能装置会使CB的投切组数减少，切换次数增多，充分证明了储能装置作为有功参与了电压的调节.不考虑电压偏差时，CB的切换组数之间变换也较小，说明不计及电压偏差时，没有利用好CB对电压偏差的调控作用.从图5可以看出，不计及电压偏差量时，储能装置的变化趋势基本一样，电压偏差主要是由CB、OLTC装置来进行控制，储能装置对电压偏差的调控作用不明显.

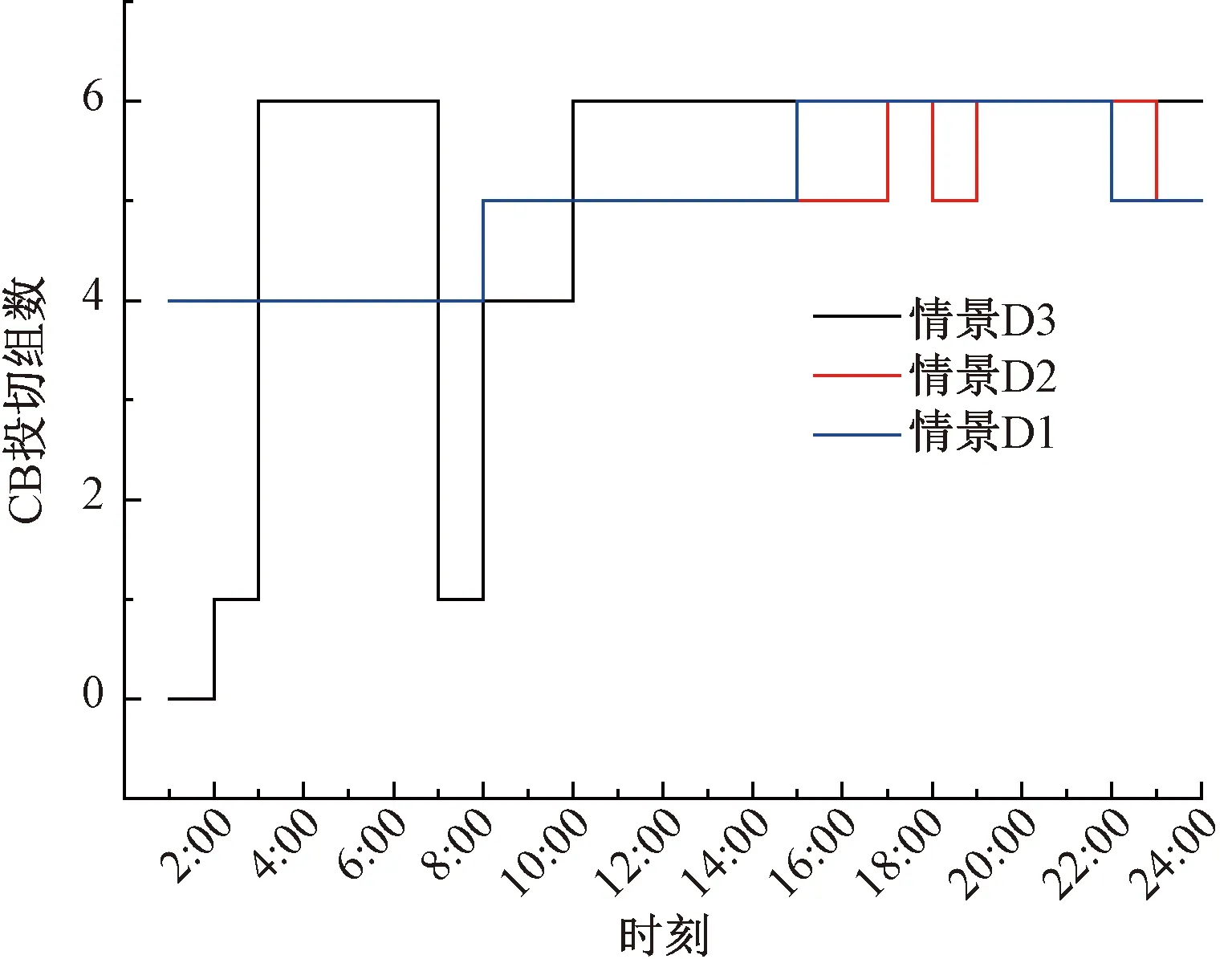
图4 5节点CB的控制策略Fig.4 CB control strategy of Node 5

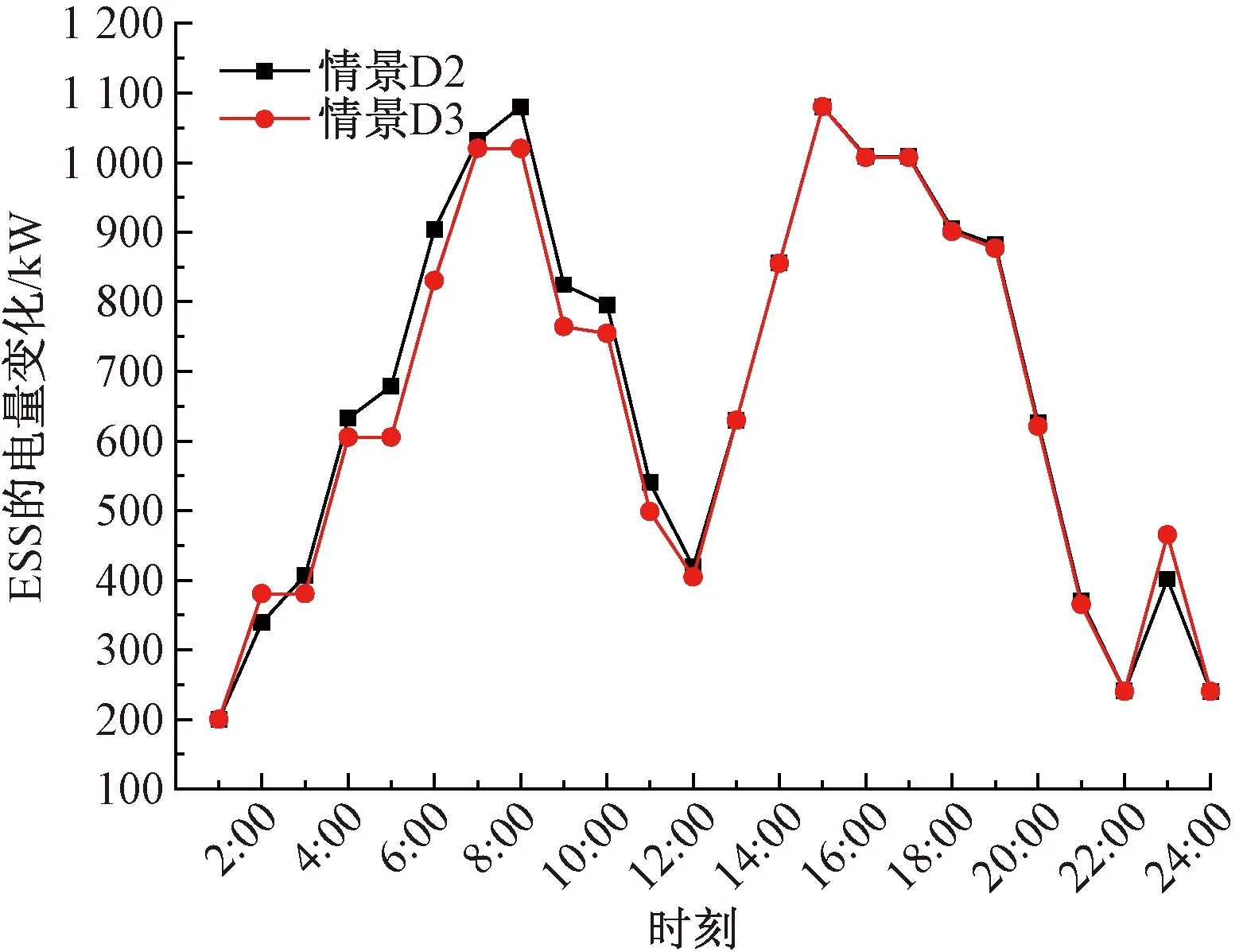
图5 节点33 ESS的控制策略Fig.5 ESS control strategy of Node 33

4 结论

(1)随着分布式电源的渗透率不断提高，其网络损耗不断减小，而弃风量逐渐增大，在笔者提出的控制策略下，电压没有出现越界.

(2)笔者提出的储能装置的充放电策略能降低网损、电压偏差等；当不将电压偏差作为优化目标时，可以适当降低网损，但是会造成较大的电压偏差，从而影响供电质量.