潜艇深度PD-模糊控制仿真研究
刘徐明,胡大斌,肖剑波,胡锦晖
(海军工程大学 动力工程学院,湖北 武汉 430033)
0 引 言
潜艇的机动控制发展至今已有较多的控制方法,但目前大多数潜艇仍采用PID控制[1]。传统的PID控制是依赖潜艇的运动模型,其模型越精确,控制效果越好[2],而潜艇运动属于多变量系统,具有严重的非线性、大惯性且易受环境中风浪流的影响[3],难以用一个精确的数学模型来描述。单一的PID控制难以满足潜艇对机动性能的要求。模糊控制是建立在人工经验基础之上,而不需要控制对象的精确数学模型[4]。但单一的模糊控制器也存在一些固有的缺陷[5],如输入变量论域不易确定、控制规则数随输入变量的增加成几何倍数增长以及可能产生稳态误差和稳态颤振等现象[6]。本文根据潜艇垂直面运动特点,设计了一种PD-模糊复合深度控制器,利用Matlab/Simulink中的建模仿真工具箱Aerospace搭建了潜艇垂直面三自由度运动模型,并在不同工况下进行仿真试验,试验结果表明了这种复合控制方法有一定的可行性。
1 潜艇垂直面运动模型
本文采用机理建模建立潜艇动力学模型,其中艇体和舵采用整体型建模方法,即将其当作一个不可分的整体进行研究。而螺旋桨推力模型采用分离型建模方法单独进行研究。本文采用国际拖曳水池会议(ITTC)及造船与轮机工程学会(SNAME)术语公报[7-8]推荐的体系,基于下述潜艇垂直面运动的三自由度运动方程开展研究。
轴向运动方程:
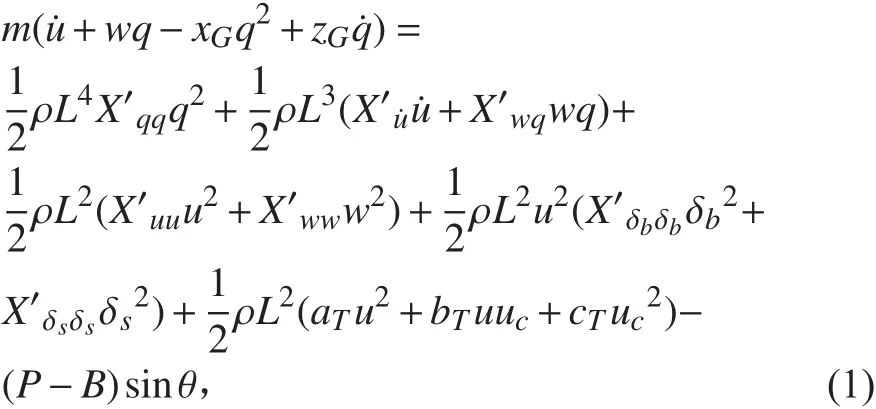
垂向运动方程:
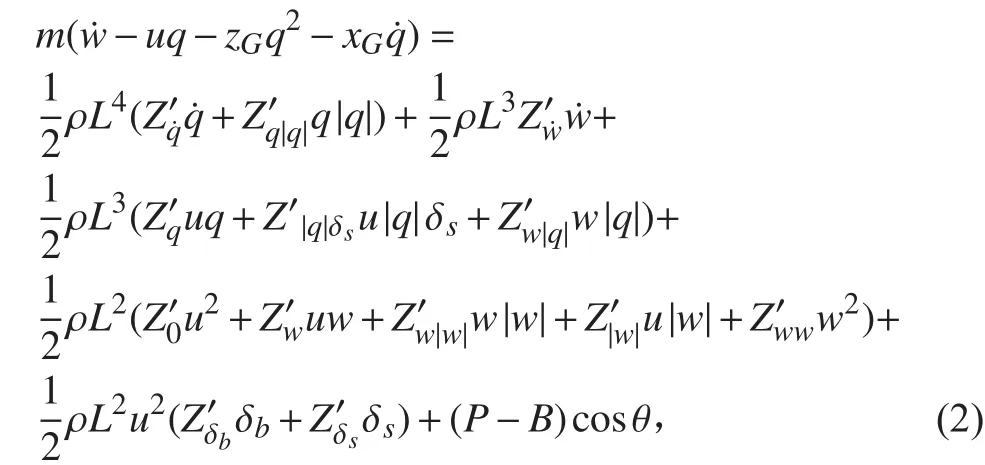
俯仰运动方程:
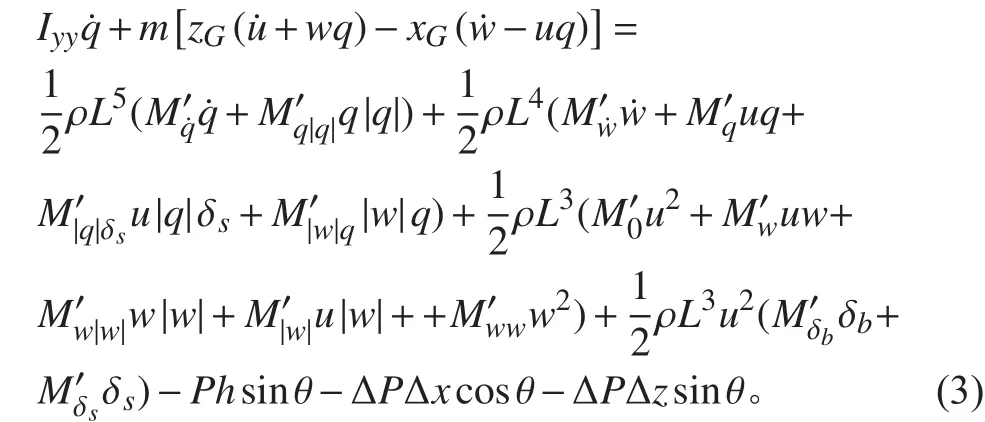
辅助方程——运动关系式:
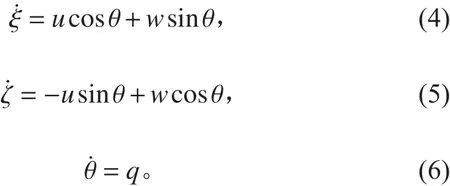
式中:m 为潜艇质量; L 为潜艇长度;ρ为海水密度;h 为稳心高;B 为水下全排水容积浮力;P为重力;u ,w ,q分别为潜艇纵向速度,垂向速度,纵倾角速度;ξ,ζ分别为潜艇在定系的横坐标,纵坐标;Iyy为潜艇对动系 y 轴的转动惯量;θ为纵倾角;xG, zG为重心在动系中的坐标;∆P 为剩余静载力;∆x ,∆z为剩余静载力作用点在动系的坐标;δb,δs分别为首,尾舵角;其余带下角标量为无因次量水动力系数。
2 潜艇深度与纵倾控制系统
深度与纵倾控制系统主要由潜艇、舵机伺服系统、传感器和控制器组成,其仿真结构框图如图1所示。其中:分别为目标深度和目标纵倾;,分别为实际深度和实际纵倾; ei, eci(i=1,2)分别为偏差和偏差变化率; u1, u2分别为指令首舵角和指令尾舵角;为环境干扰; et为复合控制器切换阈值。控制系统在Simulink中的模型如图2所示。本文采用首尾舵分离控制方式,即首舵控制深度,尾舵控制纵倾,其中深度控制器采用PD-模糊控制器,由于扶正力矩的存在,纵倾控制只采用模糊控制器即可满足机动性要求。在深度控制中,PID控制器只有在深度偏差大于PD-模糊控制器切换阈值时输出控制量,故只需考虑响应的快速性,因而去掉PID控制器的积分环节。深度PD控制器规律为:
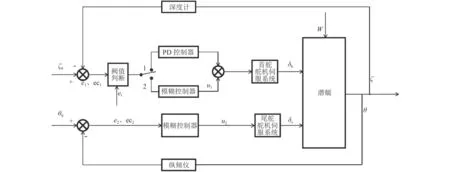
图1 深度与纵倾控制系统框图Fig. 1 Diagram of depth and pitch control system
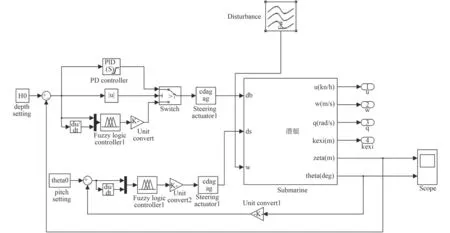
图2 深度与纵倾控制系统仿真模型Fig. 2 The simulation model of depth and pitch control system for submarine
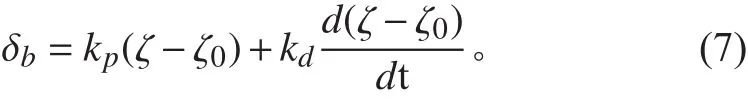
式中: kp, kd分别为比例系数和微分系数。
舵机伺服系统是一个包括纯延迟、死区、滞环、饱和等非线性特性的电动液压系统,通常可简化为一阶惯性环节,仿真时主要考虑最大舵角限制和最大转速限制,舵机伺服系统仿真模型图如图3所示。其数学形式如下:

式中: δ为实际舵角; δc为命令舵角; T为舵机时间常数; K为舵机增益;

图3 舵机伺服系统仿真模型Fig. 3 The simulation model of steering gear servo system
3 模糊控制器的设计
模糊控制器的基本结构主要由模糊化、知识库、模糊推理和清晰化等4个部分组成。本文采用首尾舵分离控制方式,故需设计2个模糊控制器、1个控制器操纵首舵来控制深度,1个控制器操纵尾舵来调整纵倾。本文选用二维的模糊控制器,即偏差及偏差变化率作为输入量,指令舵角作为输出量。其中深度模糊控制器输入变量有深度偏差和深度偏差率 ec1,输出控制量为指令首舵角 u1;纵倾模糊控制器输入变量为纵倾角偏差 e2和纵倾角偏差率,输出控制量为指令尾舵角 u2。由于2个模糊控制器结构相同,故以深度模糊控制器为例进行设计说明。
3.1 模糊化
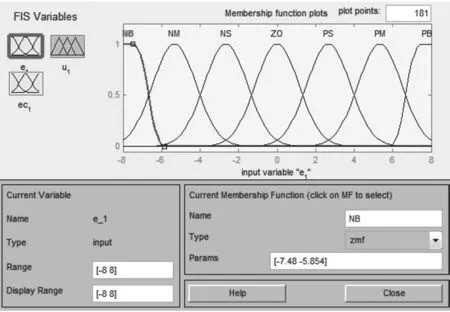
图4 深度偏差e1的隶属函数Fig. 4 Membership function of depth deviation e1
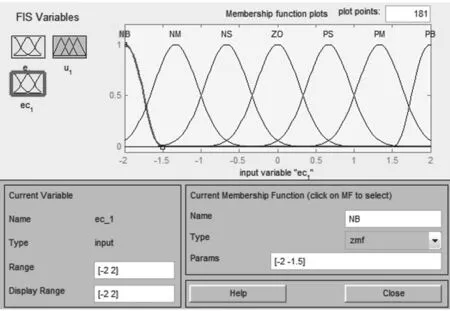
图5 深度偏差变化率ec1的隶属函数Fig. 5 Membership function of depth deviation ratio ec1
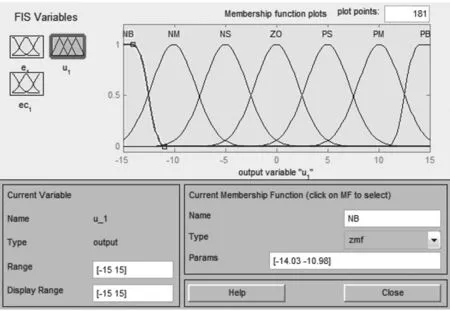
图6 指令首舵角u1的隶属函数Fig. 6 Membership function of ordered bow-rudder u1
3.2 知识库
知识库通常由数据库和规则库组成,数据库包含量化因子和隶属函数等参数。本文采用的模糊控制器的量化因子为1,隶属函数上文已说明。模糊控制系统是用一系列基于专家知识的语言来描述表达的,专家知识一般由形如“IF-THEN”条件语句构成,称为规则库。具体的控制规则,可根据采用首舵控制深度的典型阶跃响应来推导。
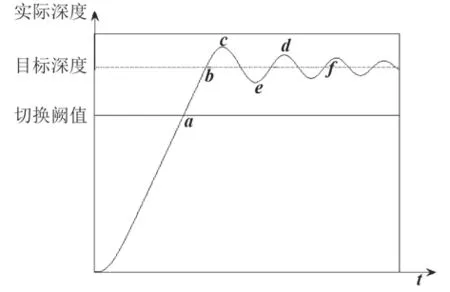
图7 潜艇深度控制过程的典型阶跃响应Fig. 7 The classic step response of submarine depth control process
图7描述了潜艇垂直面运动深度控制的典型阶跃响应,在a点之前,潜艇的深度由PD控制器控制;在a点附近,属于大偏差但有大趋势接近目标深度,故只需小舵角使深度较快地到达目标深度而不产生大的超调量,其控制规则为:if (e1is PB)and (ec1is NB) then (u1is NS);在b点附近,属于较大偏差率,需要较大的反舵防止产生较大的超调,可采用控制规则:if (e1is ZO)and (ec1is NM) then (u1is PM);在c点附近,属于较大偏差,故可用大舵角使其快速回到目标深度,其控制规则可以为:if (e1is NM)and (ec1is ZO) then (u1is PB)。在 d 点和 f点附近与b点相似,e点与c点相似。
同理可根据这样的思路,推导在其他位置时的控制规则。模糊控制规则的性能要求[9]:1)完备性,即对任意的输入应确保至少有一个可用的规则;2)在满足完备性下,尽可能减少控制规则;3)模糊控制规则之间不能有互相矛盾的地方。根据以上性能要求,可得到深度模糊控制规则如表1所示。
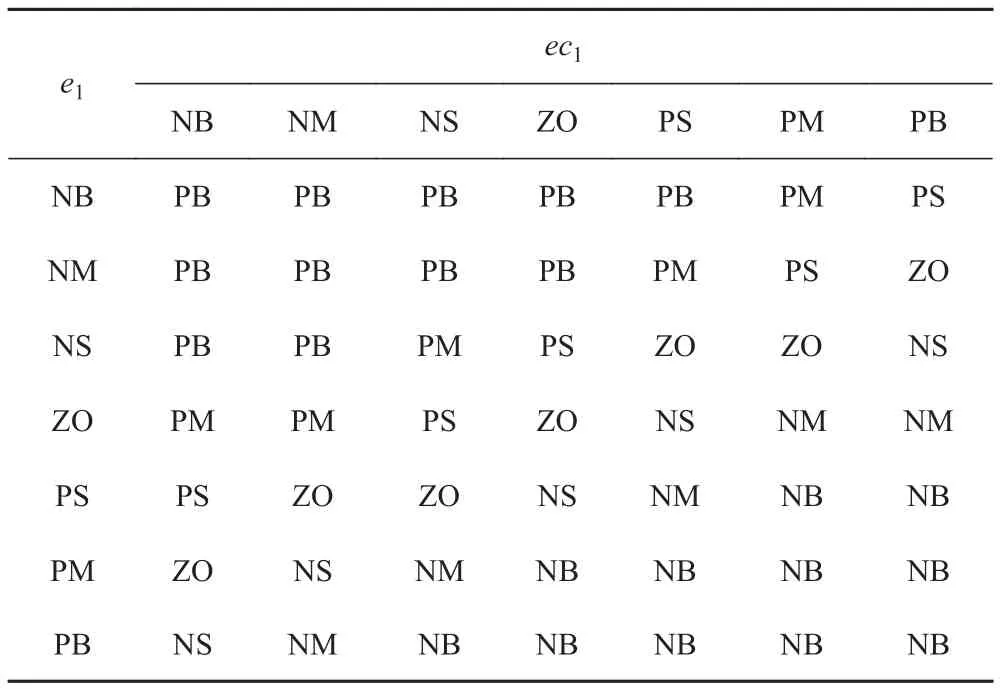
表1 深度控制规则表Tab. 1 Rule of depth control
3.3 模糊推理与清晰化
模糊推理是模糊控制器的核心组成部分,具有模拟人的基于模糊概念的推理能力,其推理是基于模糊逻辑中的蕴含关系及推理规则来进行的。模糊推理是一种近似推理,常用的推理方法有扎德(Zadeh)法、马丹尼(Mandani)法和鲍德温(Baldwin)法等,本文采用马丹尼极小运算。将模糊推理输出的模糊量转换为精确量的过程称为清晰化,常用的方法有最大隶属度法、中位数法和加权平均法(重心法),本文采用加权平均法。利用Matlab模糊工具箱可以看到各语言变量的模糊推理特性曲面,如图8所示。可以看出e1,ec1和u1的模糊推理输出特性曲面过渡平滑,没有突变,由此可知,深度模糊控制规则选择合理,可以进行仿真验证。
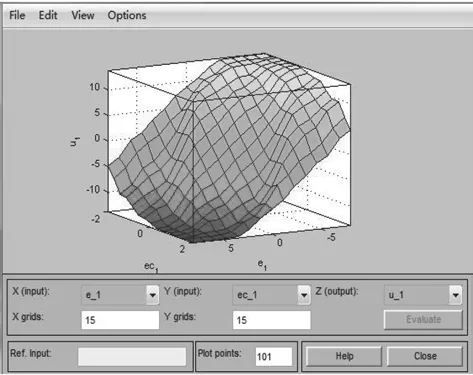
图8 深度模糊控制器的模糊推理输出特性曲面Fig. 8 Fuzzy reasoning surface of depth fuzzy controller
4 仿真与分析
用上述设计的PD-模糊控制器进行潜艇深度控制仿真试验,仿真潜艇初始状态为定深等速直航,航速为10 kn,分别采用PID控制和PD-模糊控制对潜艇进行深度控制试验(PID控制参数在各种工况下已调整至最优)。
4.1 试验结果
1)在无干扰情况下,初始深度为80 m,分别给定目标深度120 m,40 m使其下潜和上浮,仿真结果如图9~图10所示。
2)在有干扰情况下,初始深度为60 m,使其下潜至90 m,仿真结果如图11所示。图12为深度变化曲线局部放大图,图13为首舵变化曲线局部放大图。
4.2 分析
1)从图9(a)可以看出,PD-模糊控制相比于传统PID控制,具有响应速度更快,稳定时间更短,超调量更小的优点。这是由于在到达阈值之前不用考虑复合控制器的PD参数过大而引起超调,故其上升时间较短;而在到达阈值之后,复合控制器的模糊控制具有控制平缓的特点,故其稳定时间更短,超调更小。
2)通过图9~图10对比可知,在不同工况下,PID控制器需要调整参数以使控制效果达到最优,而复合控制器不需要更改参数就可以满足控制要求,说明复合控制器具有较好的适应性和鲁棒性。
3)从图11~图13可以看出,在有干扰条件下,PID控制的响应曲线震荡明显,尤其在打舵方面,这对潜艇的隐身性不利,同时也增加了舵机的磨损,而复合控制器的响应曲线变化平稳,受扰动影响较小。这说明复合控制器具有更好的抗干扰能力。
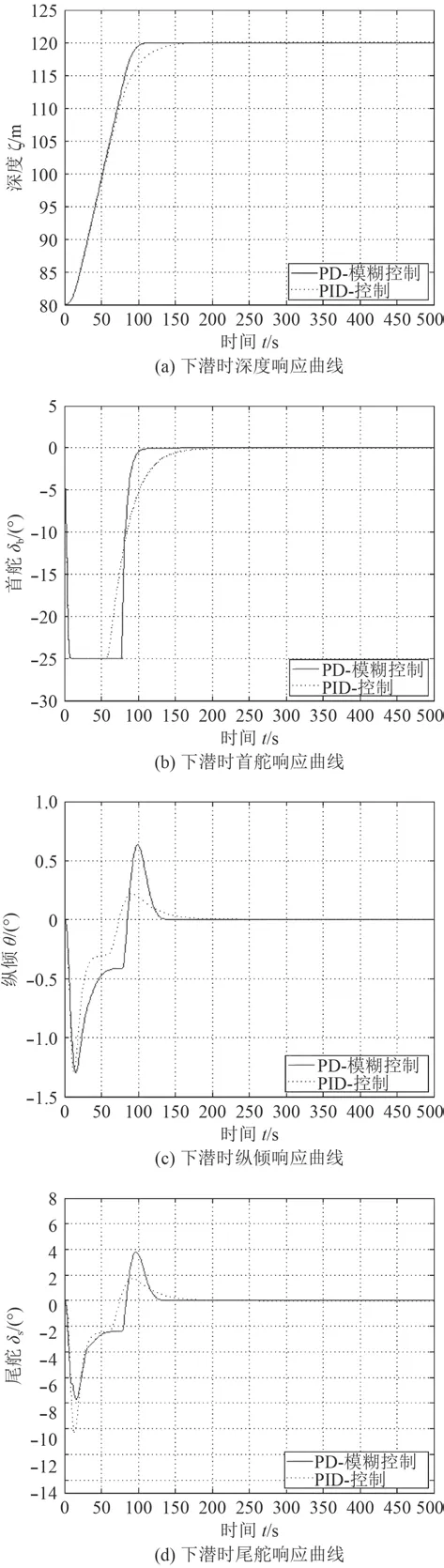
图9 下潜时各参数响应曲线Fig. 9 The response curve of each parameter when diving
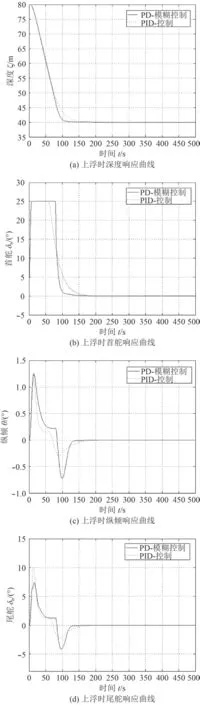
图10 上浮时各参数响应曲线Fig. 10 The response curve of each parameter when floating
4)由于模糊控制器本质上属于PD控制,会产生静态偏差,但本文所设定的阈值很小,故其静态偏差可以忽略。若还需减小静态误差,则可以引入模糊积分环节。
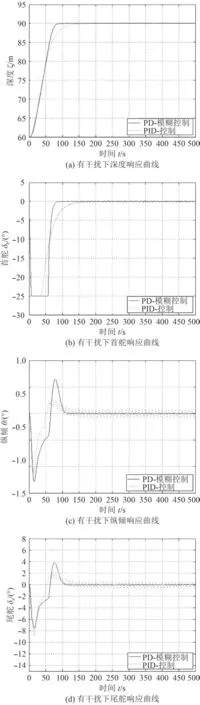
图11 有干扰下各参数响应曲线Fig. 11 The response curve of each parameter under interference
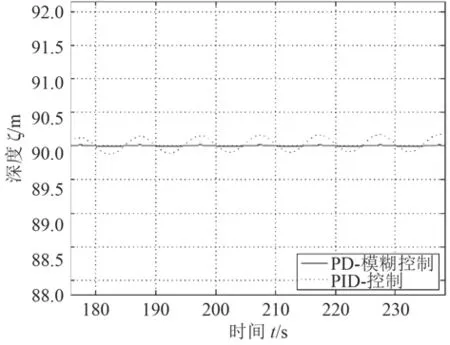
图12 深度响应曲线局部放大图Fig. 12 Partial magnification of depth response curve
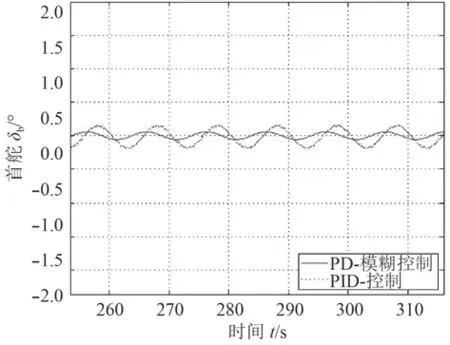
图13 首舵响应曲线放大图Fig. 13 Partial magnification of bow-rudder response curve
5 结 语
仿真试验证明本文设计的PD-模糊控制器能够简单实现潜艇深度控制的切换,具备PID控制和模糊控制的优点,有效解决了传统PID控制在有高频干扰下频繁操舵和模糊控制的论域难以确定的问题,且具有良好的快速性、稳定性和鲁棒性。

