OVT域地震数据规则化技术及应用
李 博
(中国石油化工股份有限公司石油物探技术研究院,江苏南京211103)
随着油气勘探开发目标探区的复杂程度不断增加,以及勘探经费的限制、野外施工条件的影响等,采集到的数据逐渐难以满足地震数据处理和偏移成像的等间距规则性要求。从保真成像的角度来看,理想的地震数据采集观测系统首先应满足由采样定理决定的勘探目标分辨率需求,同时满足勘探目标立体观测角张角足够大、反射界面上的立体观测角具有相同属性并且均匀分布、方位角和炮检对等间隔分布等条件[1]。近年来,宽方位高密度地震技术的应用越来越普遍,已成为致密油气藏、地层岩性油气藏等复杂油气勘探领域的关键技术方法,宽方位资料处理技术也因此成为国内外资料处理研究和试验的热点[2-4]。在各种宽方位资料处理技术中,OVT处理技术因其易于实现、使用灵活、效果优良而逐渐发展成为业界的主流方法之一。
OVT的概念最早由VERMEER[5]和CARY[6]在研究宽方位数据观测系统设计时分别独立提出,VERMEER较系统地论述了OVT采集、处理的一些基本问题[7-8],使OVT域处理技术理论基本成形。WILLIAMS等[2]从中发现了这种方法在方位各向异性速度分析和AVAZ应用方面的价值,此后,国外大量开始采用宽方位数据开展OVT处理技术的应用研究。其中包括:由于地震采集不规则导致OVT域覆盖次数不均匀,影响地震数据处理的振幅一致性,容易产生采集脚印和严重空间假频的问题[9-10];由于OVT域对偏移距的矢量化概念的应用,导致目前所采用的“束”状观测系统必然存在OVT域不规则采样问题,因此针对OVT域的规则化方法是国际上研究的热点。另外,实际地震数据中存在的主要问题是信噪比低、方位角窄、炮检点分布空间不规则[11]。这些客观存在的问题对后续的地震数据处理和成像,尤其是偏移成像会产生严重的影响,导致成像振幅出现畸变,同相轴不连续出现构造假象和岩性解释陷阱。在当前地震勘探走向精确和保真的情况下,地震数据的空间规则化是必须要解决的一个技术环节。因此,对不规则OVT域地震数据进行插值处理具有重要的实际意义。
目前,地震数据规则化方法可分为三大类。第一类是基于速度模型的规则化方法,包括反动校正方法、逆Radon变换法、反偏移方法等[12-13]。此类方法核心思想是借助速度模型或速度假设条件将非规则数据体映射到规则的数据体,模型的正确性对地震数据映射的精度影响比较大。第二类方法为基于信号分析的规则化方法,其思路是通过非规则数据采用多种约束条件下的反演方法重建规则数据的傅里叶频谱[14-16],此类方法频谱恢复的精度对于输入数据的不规则性依赖较强,由于输入数据采样密度的限制经常导致高频、高波数数据难以有效恢复。第三类规则化方法是稀疏域特征波压缩感知的方法[1],其核心思想是利用非规则采集数据的随机性和冗余性,选择合理的稀疏域表达,获得信号的压缩识别,然后进行稀疏反变换实现信号的感知插值,同时实现噪声压制,但是变换域的选择、随机采样的方式和冗余度的估计存在潜在风险性,这些因素有可能损失有效信息和增加错误信息。
目前常用的规则化方法是利用人工给予的最高频率门槛值作为迭代终止条件的频率波数域反泄露傅里叶变换方法。该算法依赖于门槛值的选择,由于规则化效果与迭代次数密切相关,因此通常为了保证规则化效果需要设定较大的门槛值,从而消耗大量的计算时间,如果选择较小门槛值则会遗漏弱反射、弱信号的处理,不能适应复杂地区的规则化需求。本文从OVT域的地震数据的排列特点出发,在最小二乘反演中采用迭代非规则傅里叶变换加权范数正则化约束,使得重建结果在有限频宽内保持数据信号不受损失,同时在能量谱约束的前提下,利用由低频信号估计的加权函数有效压制高频信号的假频问题。
1 OVT域叠前道集提取方法及流程
通常偏移距是一个标量,定义为炮点到检波点之间的距离。图1是一个野外三维工区的偏移距覆盖次数分布图(图1a)和方位角覆盖次数分布图(图1b),每个地震道的中心对应着一个方位角和一个偏移距。
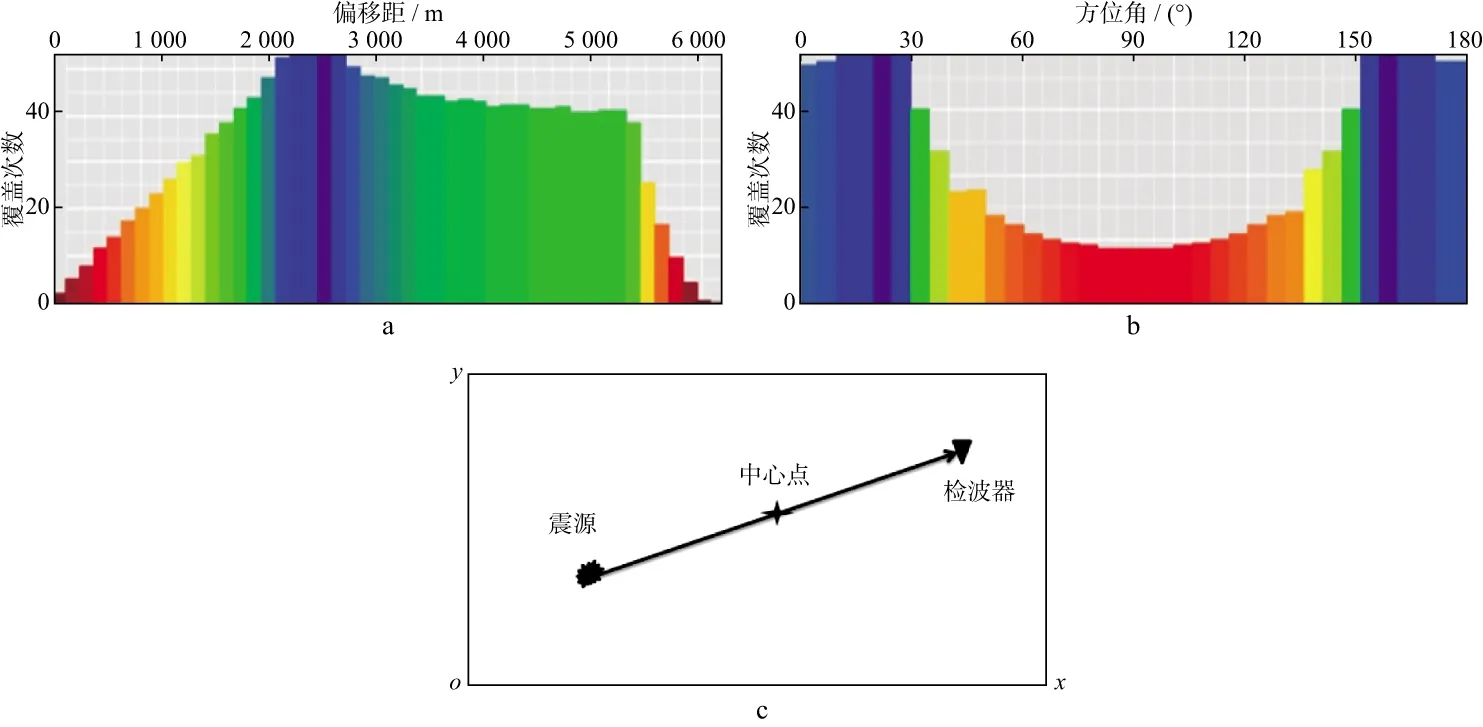
图1 偏移距覆盖次数(a)、方位角覆盖次数(b)分布与矢量偏移距(OVT)定义(c)
从图1可知按偏移距或方位角划分面元内的覆盖次数都不均匀。理论上如果设计各个方位和偏移距覆盖次数都均匀的观测系统,野外施工成本将显著增加。因此,为了提升成像振幅均匀照明的目标,需要综合考虑偏移距和方位角,这就是目前国际上流行的OVT方法,OVT直译为偏移距矢量面元,更通俗的译法为“共偏移距共方位角面元”。OVT指的是带方向的矢量偏移距,方位角作为偏移距的矢量方向。图1c中以三维工区的平面图为例,展示了矢量偏移距的定义方式,图1c中矢量方向由震源指向检波器,矢量大小为震源与检波器之间的距离。
将每个OVT面元投射到CDP面元,有的面元内会有一道或者多道,有的面元内是空道。对于多道的情况,可根据偏移距、方位角和CDP中心位置的误差最小原则,选出几何意义上的最优道,形成一个单次覆盖剖面,称之为OVT道集。图2是提取OVT道集的技术流程示意图。图2a是野外采集的原始地震数据,利用如图2b所示的网格定义划分成原始的CDP道集数据;然后将每个面元中的地震道按照方位进行筛选,每个CDP挑选方位一致的地震道(图2c),每个CDP网格中存在数量不等的地震道,但是不一定落在面元的中心点上;最后选择偏移距和与中心点的位置的均方根误差进行排序优选出一道原始数据,利用动校正技术将其移动到面元中心点上(图2d),这样就形成了需要的OVT域的叠前地震数据道集。
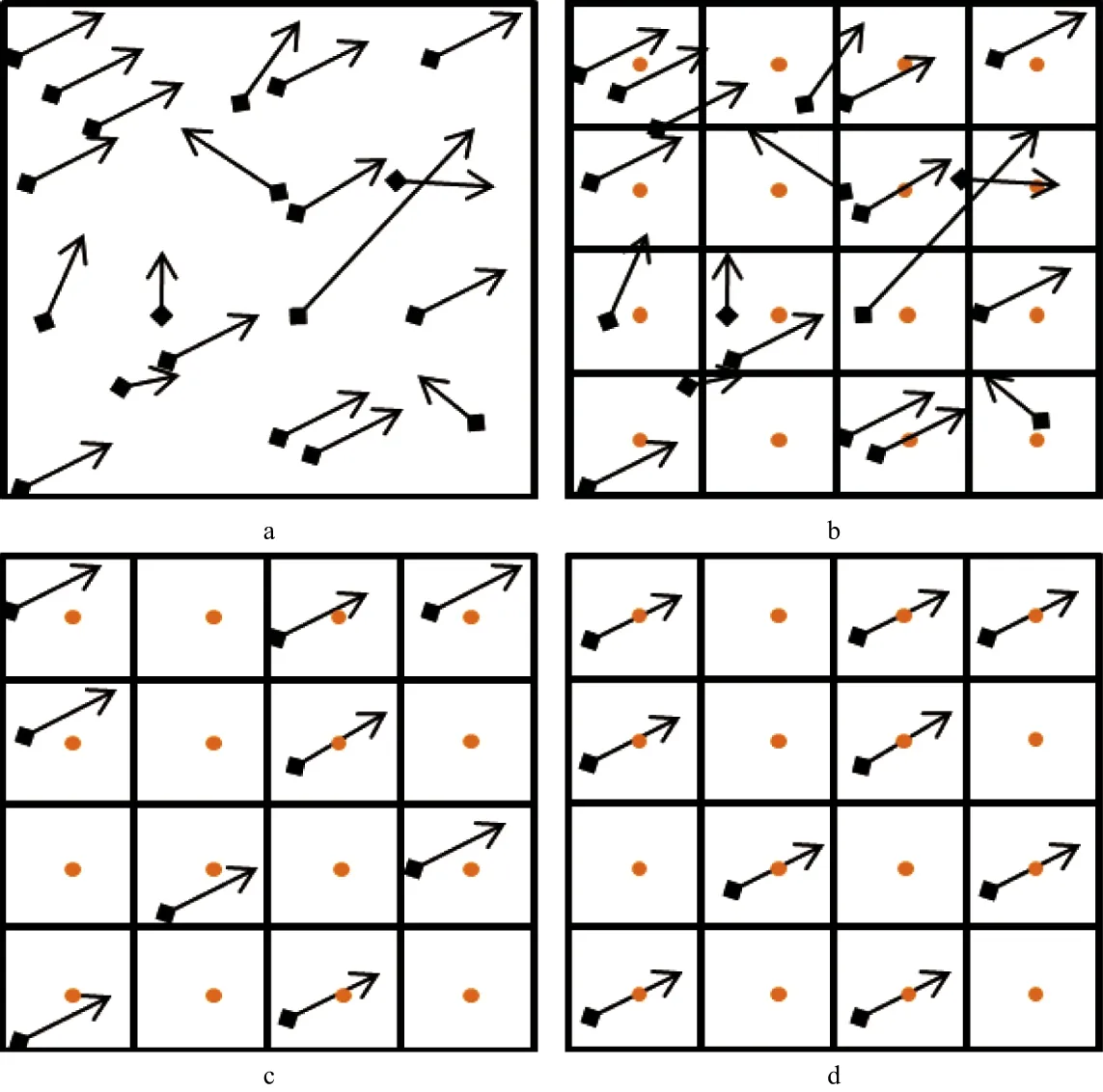
图2 OVT域道集提取示意a 原始数据; b CDP网格定义; c OVT面元定义; d 部分时差校正
可见,OVT道集中的相邻道有较好的相关性,同时也存在很多空道,必须进行规则化处理对空道内插。实际资料处理流程如图3所示,首先原始单炮数据输入后需要进行动校正处理,因此建议规则化的处理步骤中,输入的单炮已经完成了静校正、去噪、反褶积、剩余静校正、叠加速度分析等预处理。然后通过OVT的面元定义,进行OVT道集的提取。最后进行OVT道集的规则化处理,输出OVT域的规则道集,再进行宽方位的数据分析、叠加或偏移成像等后续的处理。从图3所示的处理流程来看,最关键的步骤是OVT域的地震数据规则化方法。根据不同的方位角-偏移距的采样方式可以获得OVT面元,每个面元都会插值出额外的地震道,这些额外地震道的数量,有可能会达到原始数据量的30%~40%,甚至更多。
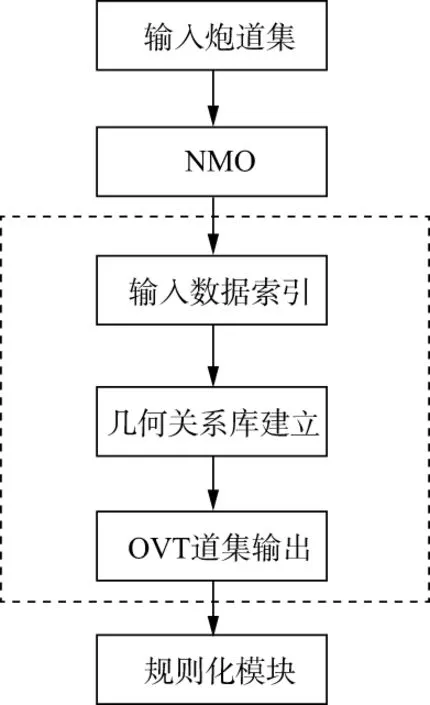
图3 OVT域规则化处理流程
2 OVT域叠前数据规则化方法
由非均匀地震数据反演重建均匀的地震数据,需要引入自适应离散傅氏变换(DFT)加权范数正则化约束,在能量谱约束下重建数据频谱。本文在最小二乘近似的框架下建立期望输出与非规则输入直接相关的目标函数,再采用预条件共扼梯度法求解反问题,保证解的稳定性和确保收敛速度。
对每一个OVT域道集数据,首先利用傅里叶变换获得频率域数据,然后对于瞬时频率f沿着空间x方向进行插值。设x表示长度为M的规则数据,x=[x1,x2,…,xM]T,y为已知的不规则观测数据,y=[y1,y2,…,yN]T,假设采样矩阵A,即可建立起规则数据与不规则数据之间的联系,其中Ai,j=δu(i),j为矩阵A对角线上的元素,其它位置均为零。假设n为噪声,建立如下线性系统:
(1)
式中:采样矩阵A为N×M阶。假设x是规则地震数据并且M=6,x=[x1,x2,x3,x4,x5,x6],非规则观测数据为y=[x1,x2,x4,x6],则公式(1)变为:
(2)
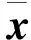
式中:F为离散傅里叶变换矩阵;F*为其共轭转置;Λ为M×M对角矩阵,Λ=diag(λk)。
(5)
则:
(6)
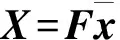
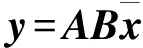
(7)
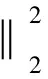
(8)

(9)
式中:P为M×M对角矩阵。当|Pk|≠0(k∈Ω)时,对角线元素为1/|Pk|,当|Pk|=0(kΩ)时,对角线元素为0。
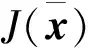
(10)
公式(10)可采用预条件共轭梯度法来求解。引入预条件方程:
则有:
(11)
式中:P-1是P的逆,是M×M的对角矩阵,AF*为非规则傅里叶变换算子。解方程(11)然后代入公式(10)可得规则化后的数据:
(12)
基于上述最小二乘反问题的构建,可以形成如下的地震数据迭代插值方法:
第一步,对不规则数据做傅里叶变换,求得能量谱的初值|Pk|(0);
第二步,非规则傅里叶变换得到算子AF*;
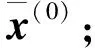
迭代终止,否则回到第三步,其中ε为设定的门槛值。
3 模型数据测试
为检验本文提出的OVT域规则化方法的可行性,对简单模型的合成数据进行抽稀后再插值。由于每个OVT道集可单独插值因此本文只展示了其中一个矢量面元的规则化成果,该方法可以推广至每个OVT道集的应用中。图4为合成的OVT数据,图4a为原始规则数据,图4b为分4道抽稀后的不规则数据。图5展示了采用本文提出的OVT域规则化方法插值的结果,图5a和5c分别为迭代10次和15次的插值结果,图5b 和图5d分别为两种迭代次数下原始道集与插值后道集的差。
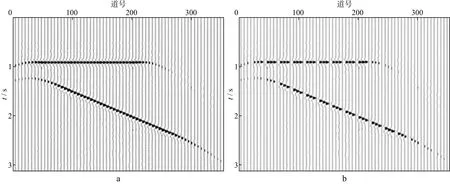
图4 原始OVT域规则数据(a)和抽稀后的不规则数据(b)
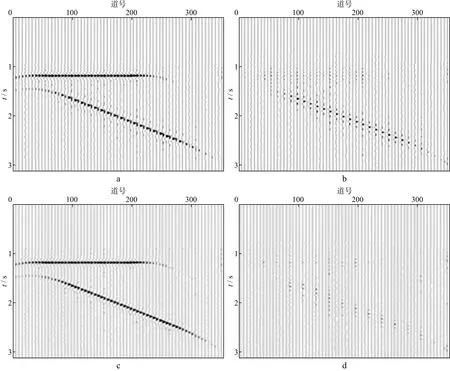
图5 迭代10次的插值结果(a)、原始道集与插值道集的差(b)以及迭代15次的插值结果(c)、原始道集与插值道集的差(d)
对比可以发现迭代10次时的反演结果(图5a)与原始数据误差较大,插值道与原始地震道振幅有明显的差异(图5b),经过15次迭代后原始道位置的反演误差基本消除,插值道位置仅仅存在很小的误差值(图5d),表明本文的插值方法的精度在预期可接受的范围。另外,具体实现过程中,可以对原始道和插值道进行区别对待,反演后只更新插值道的数据,原始道保持原始数据不变。
4 实际资料应用
为了验证本文OVT域规则化方法的有效性,实际资料选择了联片处理的3块三维数据(图6)。3块资料的采集参数如下:区块一的CMP面元75m×30m、覆盖次数36次;区块二的CMP面元75m×25m、覆盖次数44次;区块三的CMP面元50m×25m、覆盖次数48次。可见,3个区块覆盖次数较低,采集方位角也不同,如果不进行规则化处理,则存在较大的拼接误差(图7)。通过对图6中3条Inline线(Inline-1,Inline-2,Inline-3)插值前后的叠加剖面对比,来验证本文方法在实际数据处理中的有效性。
首先需要对单炮数据进行目的层主频分析,单炮数据如图8a所示,选取有效信号的区域进行频谱分析,从频谱中可看到单炮有效信号的主频为20~35Hz,高截频在70Hz左右,因此OVT域的规则化只需要进行70Hz以内的插值处理就可以提高计算效率,保证不损失有效信号的权重,无需做到奈奎斯特频率(最大频率)。
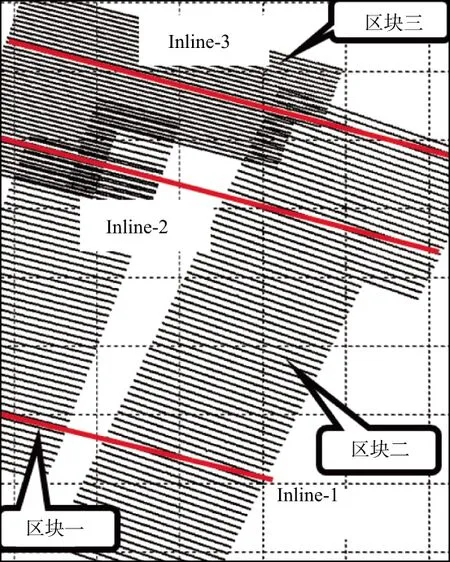
图6 3个区块位置分布

图7 三维叠加剖面拼接剖面
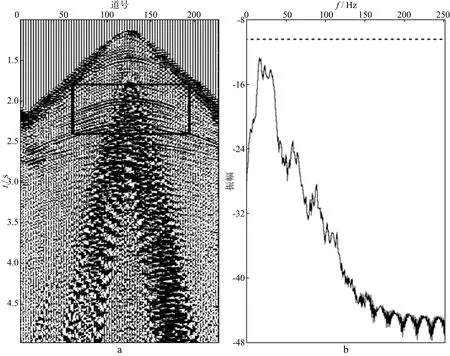
图8 单炮数据(a)及其主频分布(b)
3个区块三维资料连片拼接处理中每个区块的处理面元以及覆盖次数均不相同,可利用OVT域规则化技术将3个区块的资料统一插值为50m×25m面元的地震采集数据,处理前后的OVT域覆盖次数与道集见图9。原始数据在统一网格下的OVT域覆盖次数如图9a所示,存在严重的零覆盖问题,图9c所示的单次覆盖剖面上空道现象明显。输入的3个区块原始数据量为36GB,利用66个CPU计算节点并行计算,规则化后数据量为135.5GB,运行时间为18h 36min。结果如图9b和图9d所示,对比偏移距为500m,方位角为30°的OVT域道集规则化前后的剖面与覆盖次数,可见原始数据如果采用50m×25m加密面元进行网格定义则会存在较多的空道,而采用规则化处理后的OVT道集覆盖次数更加均匀,剖面结构更加清晰,绕射波能量保持良好,有利于偏移成像处理。
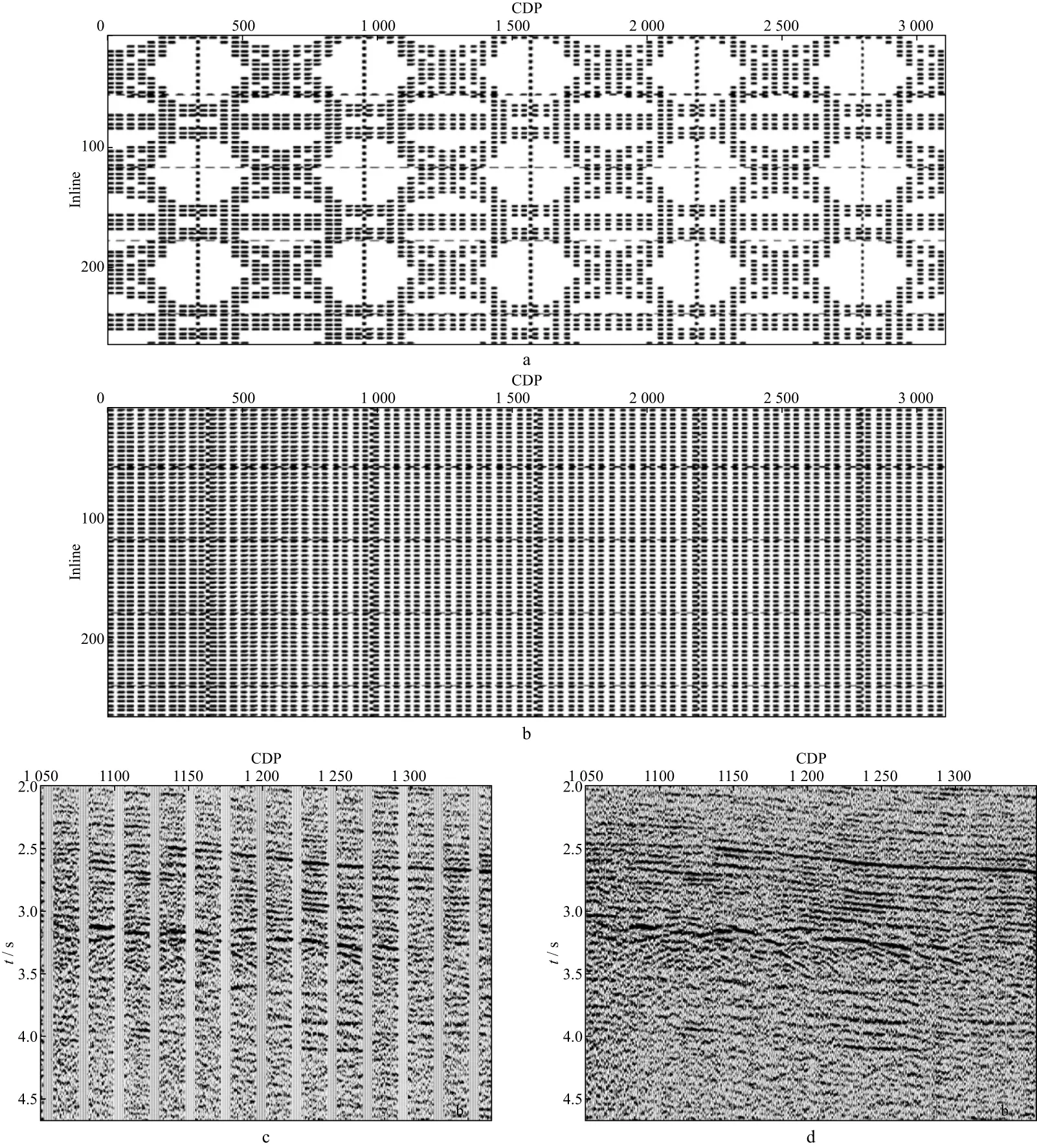
图9 OVT域覆盖次数与叠加剖面a 原始数据中偏移距为500m方位角为30°的OVT覆盖次数; b 规则化后偏移距为500m方位角为30°的OVT覆盖次数; c 原始数据的叠加剖面; d 规则化后数据的叠加剖面
将所有OVT道集进行叠加可以得到最终的叠加剖面。图10至图12分别展示了图6中3条Inline线规则化前后的叠加剖面,其中Inline-1线包含区块一和区块二并且两个区块方位角有8°误差,从原始叠加剖面(图10a)上看,拼接痕迹明显,振幅能量不均匀,剖面接口较多,难以对整个地层的横向展布进行识别,规则化处理后,剖面(图10b)的连续性明显提升,肉眼看不出拼接痕迹,振幅能量更为均衡,构造形态体现得更清晰,断层位置和接触关系的刻画更加合理。
Inline-2线包含3个区块的拼接位置,除了区块方位角不同,还有边界重合区域的高覆盖问题。从原始叠加剖面(图11a)上看,存在多处拼接痕迹,振幅能量不均匀,信噪比相对较低。
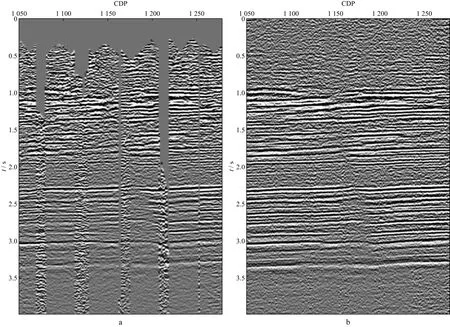
图10 Inline-1线规则化前后叠加剖面对比a 原始叠加剖面; b 规则化后叠加剖面
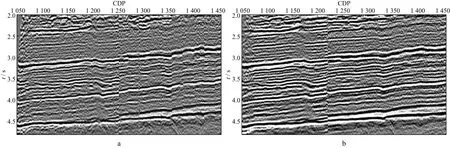
图11 Inline-2线规则化前后叠加剖面对比a 原始叠加剖面; b 规则化后叠加剖面
规则化处理后,剖面(图11b)的连续性明显提升,消除了大部分拼接痕迹,其中有一处拼接位置由于区块一和区块二的中间部分的间距达到300m以上没有采集到任何信息,超出插值置信区间的范围,因此算法自动舍去其中插值道。规则化后的剖面上,区块一和区块二的构造显示更连续,整体刻画完整清晰,剖面的整体信噪比提升,拼接部分的过渡更自然。
Inline-3线包含区块二和区块三,两个区块的拼接位置,方位角相差5°,具有边界重合区域。从原始叠加剖面(图12a)上看,由于目标输出的成像网格与区块三重合,因此从区块三到区块二的过渡中存在多处拼接痕迹,振幅能量不均匀,信噪比较低,其中的微幅度构造的成像受到影响。规则化处理后,剖面(图12b)的连续性明显提升,消除了所有拼接痕迹,构造形态更清晰,内幕反射信号增强,信噪比提升明显,微幅度构造形态没有受到插值的影响。以上结果表明本文的插值方法在保幅和提高信噪比方面均有较好的实用性。
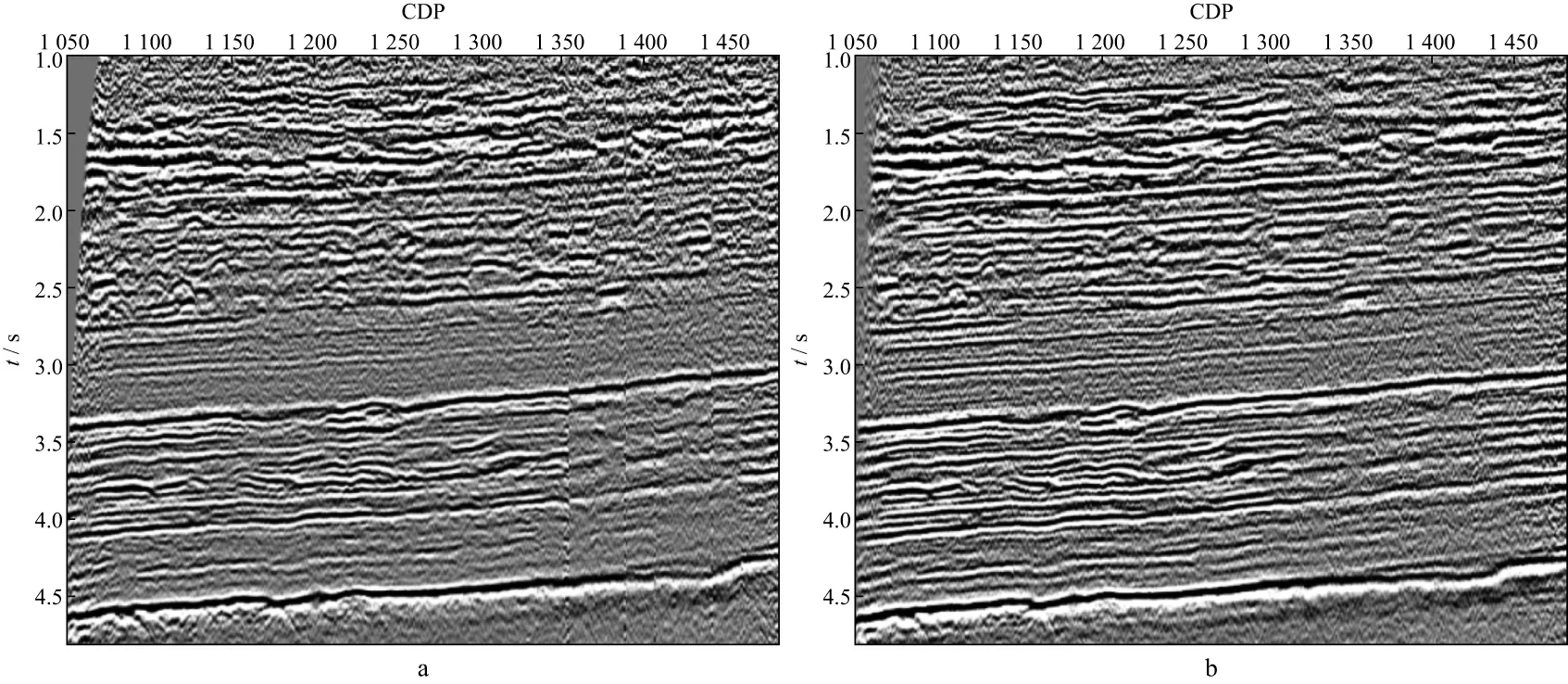
图12 Inline-3线规则化前后叠加剖面对比a 原始叠加剖面; b 规则化后叠加剖面
5 结论
本文从OVT域道集的特点出发,构建了数据插值的反问题表达形式,利用功率谱约束最小平方反演方法实现了反问题的求解,具体实现过程中采用非规则傅里叶变换与共轭梯度法实现了迭代反演算法。利用模型资料抽稀后再插值的数据与原始数据残差对比,验证了反演的精度和可行性。实际资料的三维联片处理应用结果表明本文方法可以消除非规则采集对OVT域处理的影响,在保护微幅构造和断层成像方面具有良好的应用效果,证实了本文方法的有效性和实用性。本文方法可以在宽方位OVT域处理的数据准备阶段使用,能够有效提高地震成像质量,减少偏移画弧、采集脚印等非规则采样造成的偏移噪声。
致谢:本文献给国家油储重大项目三十周年纪念会议,谨此感谢李幼铭先生的栽培和指导。

