底架边梁及上弦梁结构刚度对车体结构模态的影响*

孟 飞， 杨 冰， 阳光武， 肖守讷， 朱 涛， 邓永权

(西南交通大学 牵引动力国家重点实验室， 成都 610031)

车体振动模态频率作为表征其固有振动特性的核心指标意义重大[1-3]。优化提高车体固有振动模态频率，如一阶垂弯和一阶横弯振动频率，对改善车辆运行的平稳性，提升乘客乘坐舒适度等，具有重要的实用意义[4]。一些文献从不同角度出发，围绕诸多影响车体模态与刚度相关因素进行了研究。文献[5]以某轻型客车车体结构作为研究对象，基于一种新型半承载式车体结构分析刚度对模态的影响，并为指导该车身设计提供参考；文献[6-7]从设备悬吊刚度的角度，研究设备悬吊刚度影响下的车体模态变化规律，为找出最优设备悬吊刚度提供参考；文献[8]以车体内部结构上弦梁的结构刚度为变量，研究其对车体模态的影响，为实际车体上弦梁参数选择提供一定的依据。

底架是整车中承载的最为关键的部分，而底架边梁又是底架承载的关键结构；对于侧墙和车顶，上弦梁是二者保证连接的关键部位。通过改变底架边梁及上弦梁相关参数，研究它们的结构刚度变化对车体一阶垂弯和横弯模态的影响。以25G型硬座车钢结构车体为研究对象，保证计算精度不冗余为前提建立足够精细有限元模型，改变底架边梁、上弦梁厚度参数，研究二者单位质量截面惯性矩变化对车体模态频率的影响规律。

1 25G型硬座车钢结构车体主要技术参数

25G型硬座车钢结构车体为无中梁薄壁筒形整体承载的全钢焊接结构。钢结构车体中，厚度为6 mm及以下的钢板采用的是高耐候钢板，包括底架两侧地板和车体蒙皮，型钢和6 mm以上的钢板用普通热轧碳素钢。表1列出了车体主要的一些参数。

表1 车体主要技术参数

2 车体有限元模型描述

关于有限元模型的建立，除了考虑该钢结构车体自身的构件排布、几何形状以及受力特点这些主观条件，还有计算精度这一客观条件要求。在计算精度足够的条件下，平衡考虑计算精度和计算时长，确定单元尺寸为20 mm。车体中绝大多数为板梁构件，有限元方法模拟这种厚度尺寸相比另两个方向很小的部件，以板壳单元CQUAD4和CTRIA3这些低阶二维单元进行离散；其中有一些部件几何形状比较复杂或者相对较小，诸如心盘、车钩座、从板座，用3D单元CHEXA和CTETRA离散；车体中涉及的起连接作用的螺栓、螺钉用梁单元CBEAM、刚性连接单元RBE2组合模拟；涉及的焊点用CWELD单元模拟。最终，表2显示了整车钢结构有限元模型中所包含的单元类型和数量，图1为整车有限元模型。

表2 整车有限元模型中所包含的单元类型和数量

图1 车体有限元模型图

3 底架边梁及上弦梁结构刚度

底架边梁是车体底架和侧墙载荷传递的唯一构件，同时也是车体关键的承载构件，对车体自身固有振动产生重要影响；而连接车顶和侧墙的唯一构件上弦梁，起两者载荷传递的关键作用，其对车体自由振动模态的影响也比较大。两种贯穿性纵向梁的横截面均为类槽型截面，其截面形心位置分别如图2中黑点标记C1和C2所示。对于底架边梁和上弦梁，其垂向和横向弯曲刚度

分别为EIy1、EIz1、EIy2、EIz2，其中，下标中1和2分别指底架边梁和上弦梁。惯性矩可分别表示为：

(1)

(2)

式(1)中Iy1、Iz1和式(2)中Iy2、Iz2分别为底架边梁、上弦梁对各自形心y轴、z轴的截面惯性矩，dA为截面的微面积，E为材料的弹性模量。

值得一提的是，在求解底架边梁和上弦梁对各自形心y和z轴的截面惯性矩时，根据相关材料力学知识，用平行移轴公式以组合图形形式对两种构件惯性矩进行求解[9]。

Iy=IyC+a2A

(3)

Iz=IzC+b2A

(4)

底架边梁和上弦梁二者整个结构件中各处材料使用相同，可用截面惯性矩来等效替代底架边梁和上弦梁的结构刚度。基于二者均为等厚构件，截面形状不变，改变其厚度参数，使截面的惯性矩随之变化从而改变它们的结构刚度。需要注意的是，底架边梁和上弦梁的厚度发生变化，质量也会随之变化，为把质量因素纳入考虑，引入单位质量惯性矩，研究单位质量刚度对车体振动模态频率的影响。

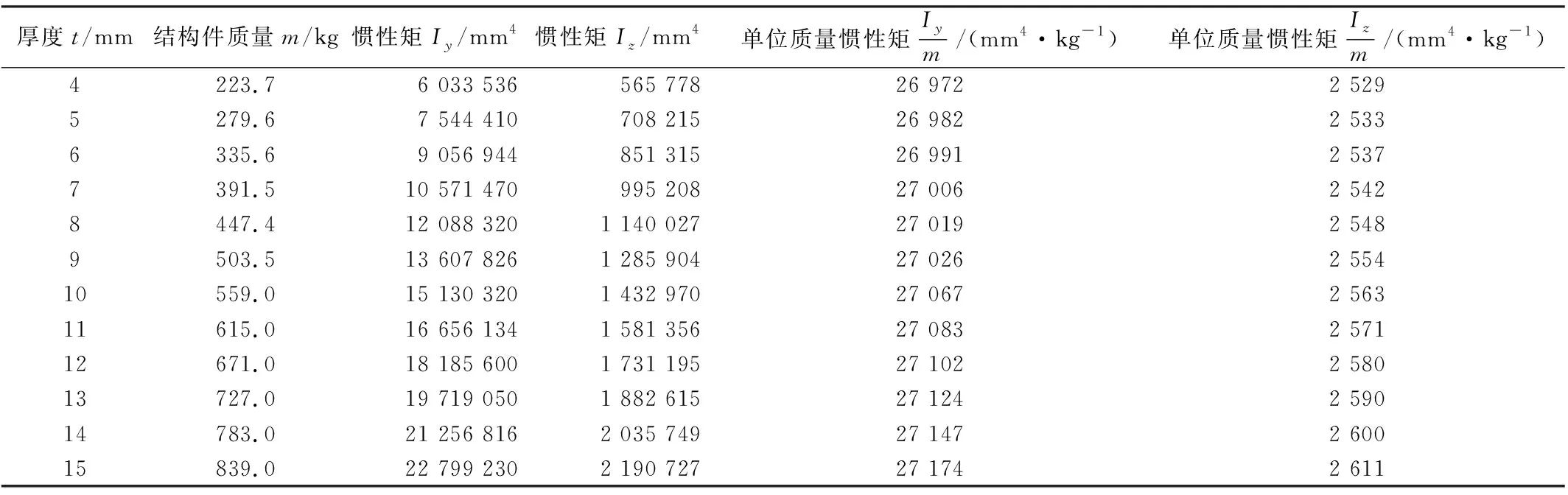
表3 底架边梁不同厚度下结构参数

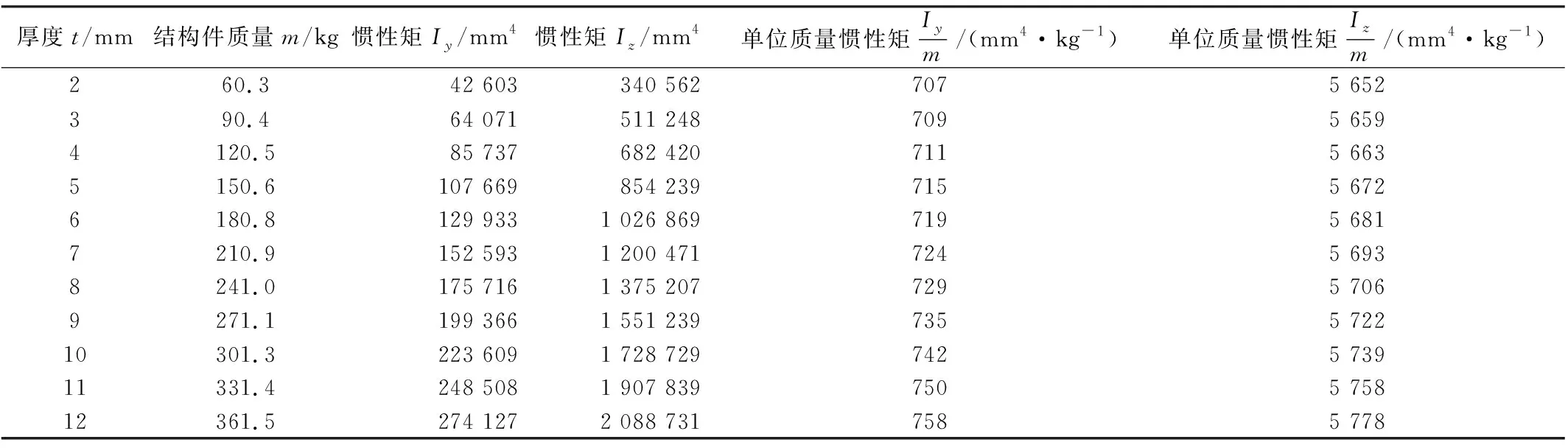
表4 上弦梁不同厚度下结构参数

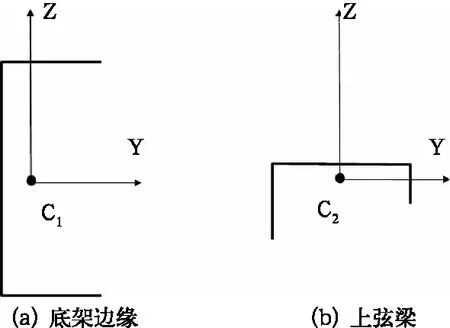
图2 底架边梁和上弦梁横截面形状

考虑到底架边梁和上弦梁承载位置和承载能力大小不同，底架边梁初始厚度取4 mm，上弦梁厚度初始值取2 mm，增量步长均取1 mm，依次增加厚度计算截面垂向和横向惯性矩，最终底架边梁增至14 mm，上弦梁增至12 mm。表3、表4分别罗列底架边梁和上弦梁渐变厚度下的相关结构参数计算结果。

4 底架边梁和上弦梁刚度对车体模态的影响分析

在车体钢结构有限元模型基础上，分别单独改变底架边梁或上弦梁厚度这一参数，计算不同单位质量惯性矩以及不同单位质量惯性矩下车体钢结构的一阶垂弯和一阶横弯频率，结果列入表3和表4中。

为更明了直观展示底架边梁和上弦梁两者结构刚度对车体模态的影响，基于表3和表4中的数据，绘制图3和图4所示折线图。

由图表可知，在底架边梁和上弦梁材料相同，弹性模量E一定的情况下，车体一阶横弯频率随底架边梁和上弦梁单位质量惯性矩的增加均呈稳步递增的趋势；车体一阶垂弯频率随底架边梁单位质量惯性矩的增加也稳步递增，但车体一阶垂弯频率随上弦梁单位质量惯性矩的增加则基本保持不变。

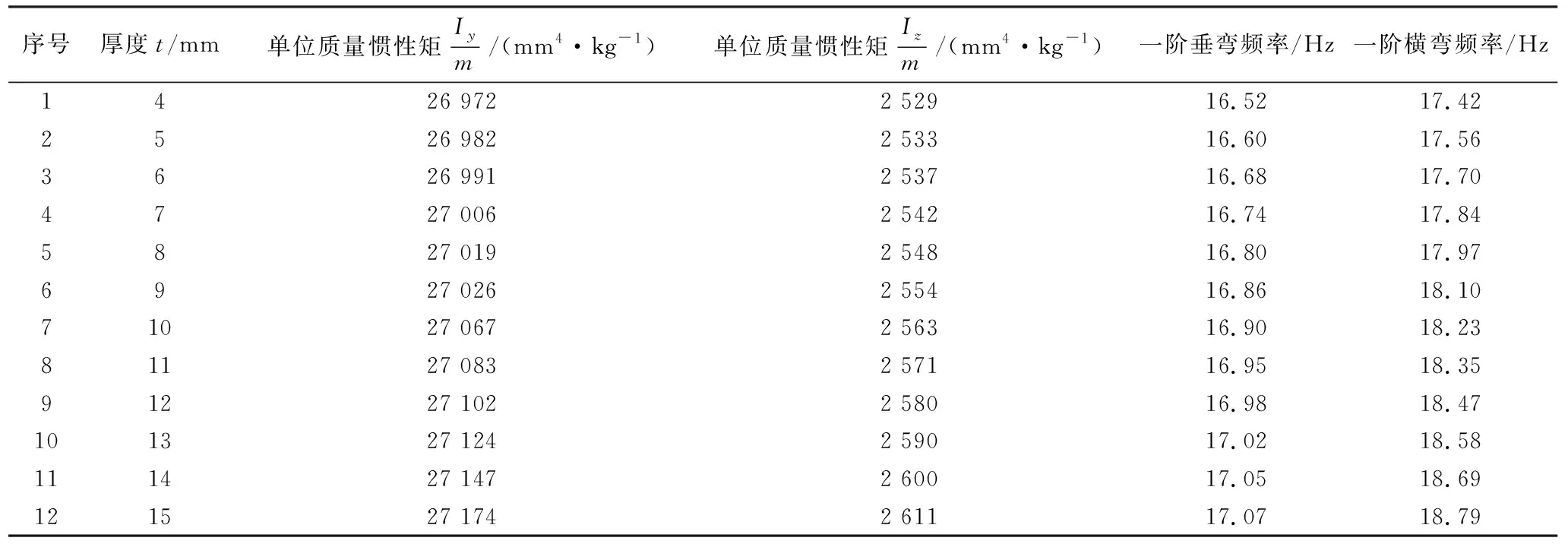
表5 底架边梁不同厚度单位质量惯性矩和对应模态频率

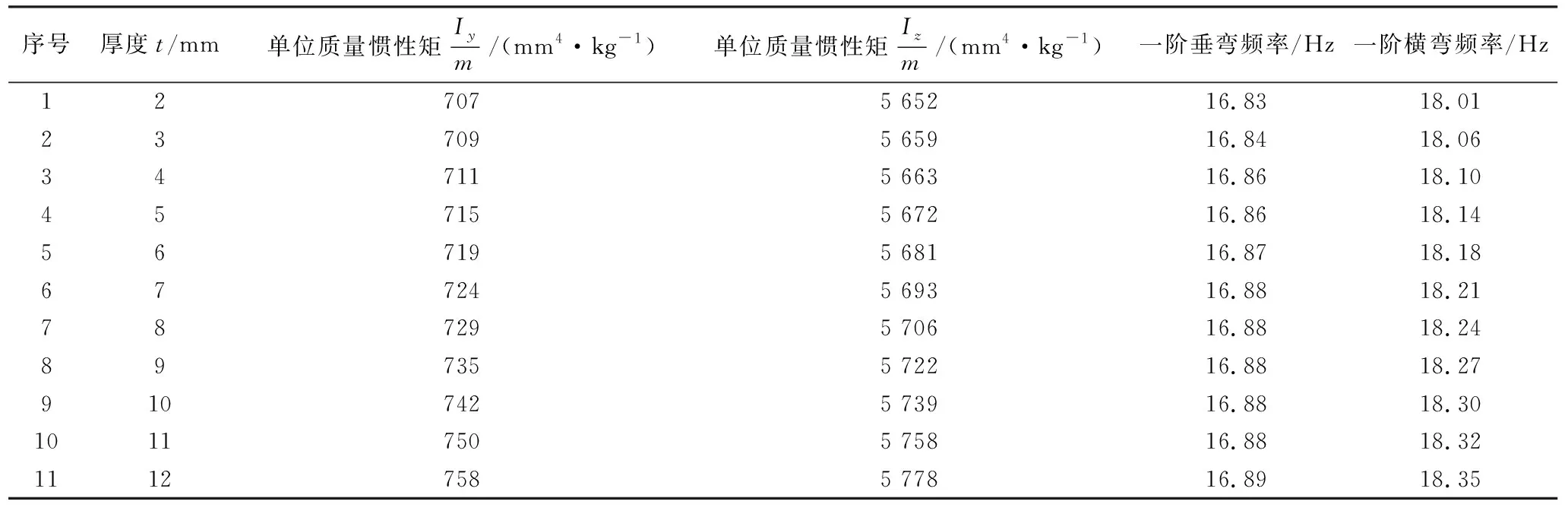
表6 上弦梁不同厚度下单位质量惯性矩对应的模态频率

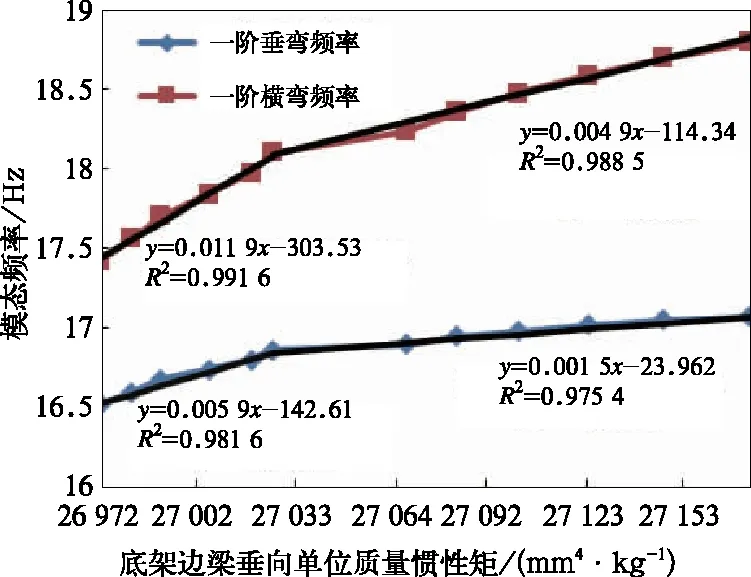
图3 车体模态频率随底架边梁的变化

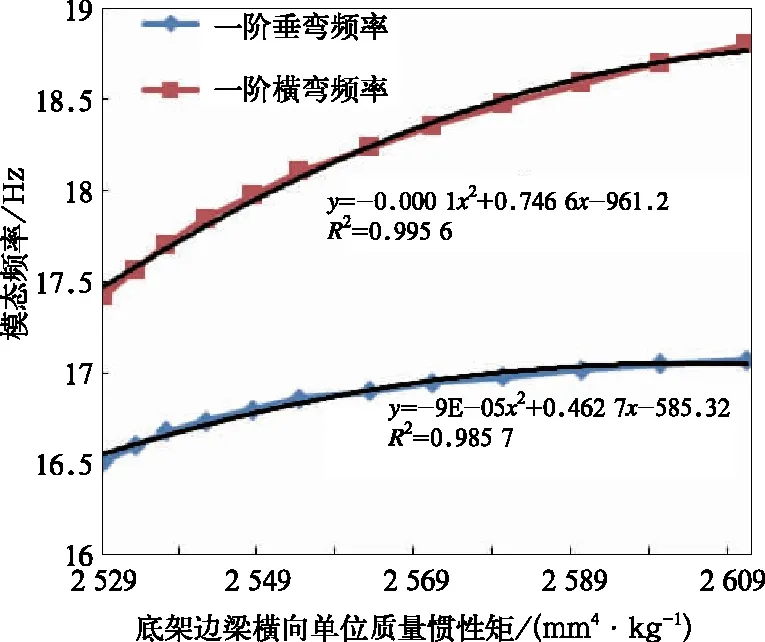
图4 车体模态频率随底架边梁的变化

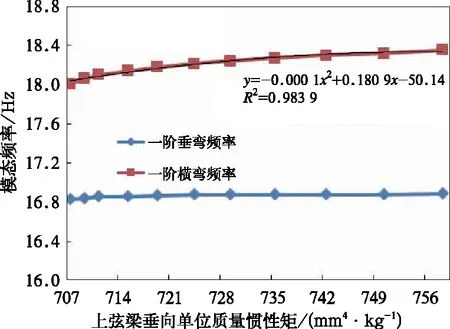
图5 车体模态频率随上弦梁的变化

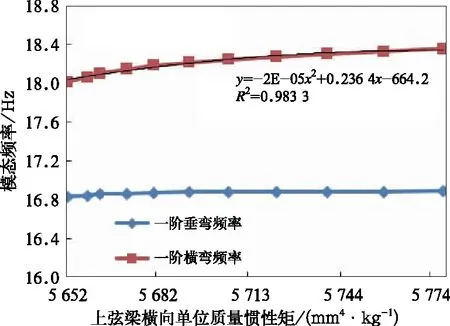
图6 车体模态频率随上弦梁的变化

5 结 论

以25G型硬座车钢结构车体为研究对象，通过改变底架边梁和上弦梁结构单位质量惯性矩及刚度，研究了底架边梁和上弦梁刚度变化对车体模态的影响，得出结论如下：

(1)车体一阶垂弯频率随底架边梁垂向刚度增加先以较高斜率的线性关系递增，然后以较小斜率的线性关系递增，车体一阶横弯频率的变化形式与之类似；车体一阶垂弯频率和一阶横弯频率则随底架边梁横向刚度增加以二次多项式函数形式递增。

(2)车体一阶垂弯频率随着上弦梁结构刚度的增加近乎不变；车体一阶横弯频率随着上弦梁结构刚度增加呈二次多项式关系递增。

(3)相对于上弦梁，增加底架边梁结构刚度对车体一阶垂弯和一阶横弯模态频率的提升更为明显。合理改变底架边梁和上弦梁单位质量刚度是实现车体结构模态优化设计的可行路径之一。