基于全局敏感性分析和PE-HMGE的轴承润滑特性优化*

李林洁，韦静思，何志良，陈 宇，占文锋

（广州汽车集团有限公司汽车工程研究院，广州 511434）

前言

摩擦损失是发动机能量损耗的主要原因之一，降低发动机摩擦损失对汽车节能减排具有重要意义。其中，轴承摩擦副是发动机的重要组成部分，其润滑性能的好坏直接影响发动机的性能及使用寿命。近年来，采用弹性流体动力学（elasto-hydrodynamic，EHD）对轴承润滑特性进行分析的方法逐渐代替了传统经典流体动力润滑方法，成为主流。申立中等［1］对柴油机连杆大头轴承进行EHD模拟计算，重点研究了轴承相对平均间隙、曲柄销油孔直径和轴瓦宽度对大头轴承润滑特性的影响。

随着油耗和排放法规的日益严格，对于轴承的要求不能仅局限于其承载和润滑能力满足需求，而是在上述前提下，尽可能降低摩擦功耗和消耗的机油量，以提高发动机有效功率，改善燃油经济性。这需要对轴承进行以多目标优化为基础的分析与设计。文献中也有这方面相应的研究成果，张俊红等［2］采用极差分析的方法确定了影响最小油膜厚度、最大油膜压力和摩擦损失功率因素的主次关系，利用BP神经网络理论建立了主轴承润滑特性模型，并对影响润滑特性的主要参数进行了优化。

由于EHD采用有限元法求解轴颈、轴瓦和轴承壁的弹性变形，用有限差分法求解雷诺方程，整个过程涉及有限单元网格与有限差分网格之间的相互映射，因此计算成本过高，很难满足优化设计的计算要求。所以，建立准确表征轴承润滑特性数值模型是对轴承进行准确多目标优化设计的关键。本文中从多体动力学角度对某汽油发动机主轴承进行EHD分析，并通过拆除倒拖摩擦功试验方法校验仿真模型。针对主轴承润滑系统非线性的特点，利于基于方差的全局敏感性分析方法——Sobol法［3］，定量分析输入变量对系统输出的影响程度，确定敏感性参数。运用克里格方法（Kriging）［4］建立可以准确表征主轴承润滑特性的数学模型，采用具有良好的探索性能的全局多目标梯度算法——PE-HMGE优化算法［5］，计算目标函数Pareto前沿个数，并重构Kriging模型，从而实现主轴承润滑特性多目标优化设计。

1 理论介绍

1.1 全局敏感性分析理论

基于方差的Sobol全局敏感性分析［3］是一种定量分析方法，其核心思想是将模型分解为单个参数及参数之间相互组合的函数，采用蒙特卡洛估计［6］得到参数的各阶次敏感度，具体方法如下。

假设系统的设计参数个数为k，在所有设计参数的初始设计空间内随机抽样n次，共抽取A，B两个矩阵，如式（1）所示，其中，矩阵的每一行表示k个参数的组合。

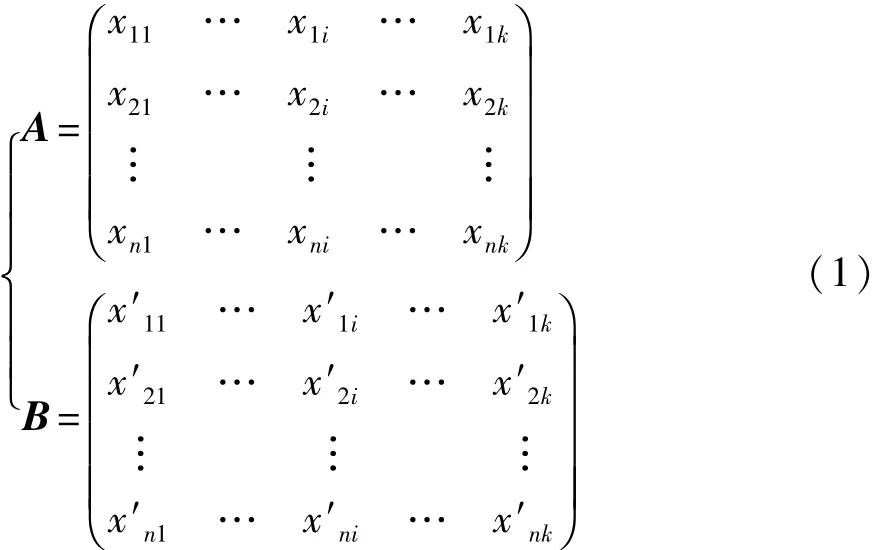
将式（1）中矩阵A的第i列换成矩阵B的第i列，其余列保持不变，得矩阵记为Ci；再将矩阵B的第i列换成矩阵A的第i列，其余列保持不变，得到矩阵记为 C-i，如式（2）所示：

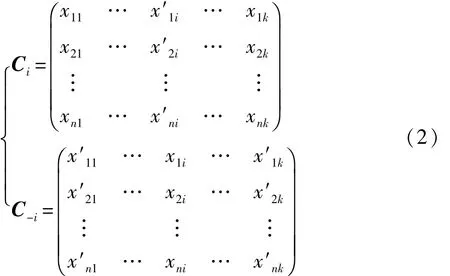
将每组设计参数分别代入到系统模型中进行计算，可得到对应每组设计参数的输出响应值，则系统响应的方差估计和参数的敏感性指标计算如式（3）～（6）所示：

输入参数 xi的主效应指标的估计为

输入参数 xi的全效应指标的估计为

1.2 K riging模型及优化方法

Kriging模型采用的是最优内插法，是一种基于统计理论的估计方差最小的无偏估计模型，其数学表达式为

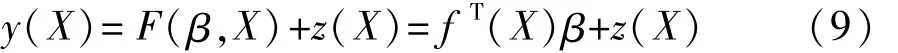
式中：β为回归系数；fT（X）为回归模型；z（X）为随机分布误差。

在初始设计变量及设计空间S确定的条件下，采用优化的拉丁方抽样方法对设计空间进行抽样。

式中：n为设计参数的个数；N1为构造Kriging代理模型所需的最少点。

利用初始样本点和响应值建立Kriging初始模型。为保证初始模型在局部的精度，优化迭代过程中，模型应不断使用新增样本点进行更新，新增样本点个数的确定方法如下所述。

引入适应度函数［8］Gi，其表达式为

式中：Gi为第i个点的适应度为第 i个点第 k个目标值的归一化值，k=1，2，…，m；l为前沿指数，这里取值为1。当Pareto前沿点密集和均匀分布时，所有的Pareto点的适应度值都趋近1。

首次迭代时，利用式（11）计算得出的Pareto前沿点个数，记为M1；后续迭代时，提取第一次样本点和本次迭代之前所有轮迭代的新增样本点，重构Kriging模型，求解Pareto解个数，记为Mq，其中q为迭代次数。将M1和Mq合并在一起，再进行适应度计算，重新确定Pareto前沿点个数，记为Qq。新增样本点数确定之后，确定新增样本点的设计空间，其确定方法如下所述。

初步确定新增样本点设计空间大小。设第q次迭代新增样本点空间为

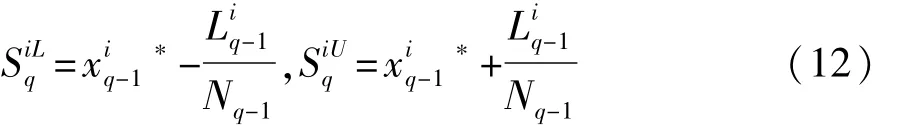
在新的设计空间内，采用具有良好的探索性能的全局多目标梯度算法——PE-HMGE优化算法［5］，选择接近Pareto前沿的个体，将第q次迭代中适应度值最接近1的那组数据作为第k个目标的最优解xkq*，将其代入到分析模型中得到最优目标值f（xkq*）。

迭代过程中，判断第k个目标在第q次迭代和第q-1次迭代产生的最优目标函数值的相对误差是否满足收敛值，若满足，则f（xkq*）即为最优值，优化流程结束；如不满足则继续迭代，直到满足收敛准则，整个分析过程的流程如图1所示。

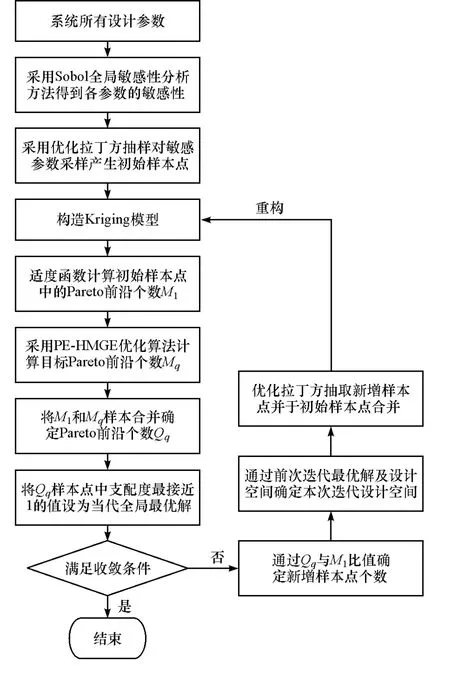
图1 多参数全局敏感性分析和优化流程

2 模型建立

2.1 曲轴系 -缸体多体动力学模型

本文中运用AVL的Excite Power Unit平台建立曲轴系 -缸体多体动力学模型，主要包括了曲轴、连杆、缸体、轴瓦等部件模块，其中主轴承主要设计参数如表1所示。

表1 主轴承主要参数

2.2 主轴承EHD仿真结果分析

为更准确计算轴承的润滑特性，主轴承采用EHD（elastic hydro-dynamic）轴承模型。本文轴承润滑特性分析中，采用峰值油膜压力（peak oil film pressure，POFP）和最小油膜厚度（minimum oil film thickness，MOFT）表示轴承的承载能力，峰值粗糙接触压力（peak asperity contact pressure，PASP）和总摩擦损失（total friction power loss，TFPL）表示轴承的润滑性能。

POFP是轴承油膜压力的最大值，一般POFP限值为：Plimit=HB／0.102，其中HB为材料的布氏硬度；若轴瓦和轴颈的表面粗糙度均方差分别为σ1和σ2，则润滑表面的合成均方差即峰值粗糙度为：σa=建立流体动压润滑的最低要求是MOFT不小于σa；PASP越小，表明润滑性能越好，通常不大于100MPa；TFPL是液动摩擦损失和粗糙摩擦损失之和。

2.3 曲轴摩擦功试验

本文中采用倒拖法分解摩擦功，发动机仅装配曲轴，去除其他附件系统，在不影响曲轴平衡率的前提下，堵塞油道。测试台架外界冷却液和机油温度及压力控制系统，调节冷却液和机油温度恒定，同时保证主油道油压、进出水压与发动机正常运行时一致，调节转速不点火倒拖，测量转矩值。图2为曲轴摩擦功测试结果和曲轴EHD仿真结果对比，试验和仿真结果在全转速工况下变化趋势基本一致，利用试验结果校验仿真模型，通过仿真手段进行参数研究，优化结构设计。

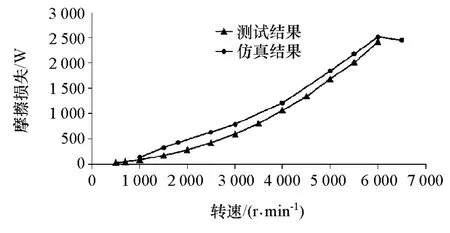
图2 曲轴主轴承摩擦损失

2.4 基于方差的全局敏感性分析

以第2主轴承为例，对发动机主轴承各参数进行敏感度分析。主轴承可考虑的参数包括轴承宽度、轴承间隙、轴瓦磨损量、轴颈鼓型量、机油动力黏度、供油压力等，如果全部参与计算，设计空间维数高达12维，必须增加采样点数来描述设计空间的信息，从而增加计算规模。通过灵敏度分析，摒弃非敏感参数，精简模型，降低计算规模。采用蒙特卡罗方法抽取104个样本点，分别代表A，B两个矩阵，通过Sobol全局敏感性分析计算各参数的主效应，结果如表2所示。

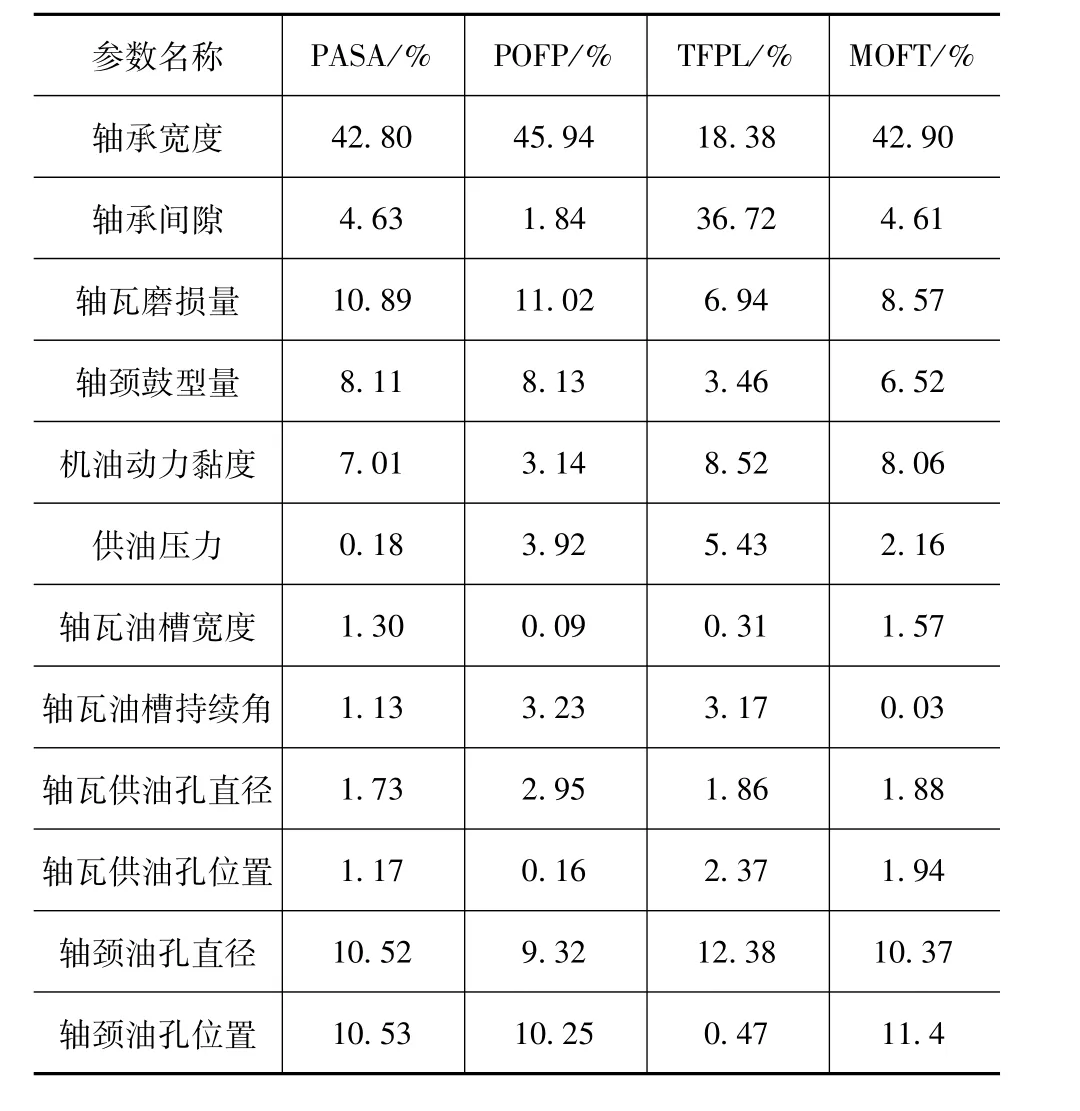
表2 全局敏感性分析结果

2.5 主轴承K riging润滑特性数值模型

根据全局敏感性分析的结果，选择轴承宽度、轴承间隙、轴瓦磨损量、轴颈油孔直径和轴颈油孔位置5个参数为设计变量。数值模型如下，

max MOFT

min POFP，PASP，TFPL

s.t.MOFT≥0.8μm

POFP≤200MPa

PASP≤60MPa

应用前文中提出的基于PE-HMGE优化算法的模型优化方法，重构Kriging润滑特性数值模型。随机选取5组设计变量，对比仿真模型和优化模型计算结果，模型精度如表3～表6所示。

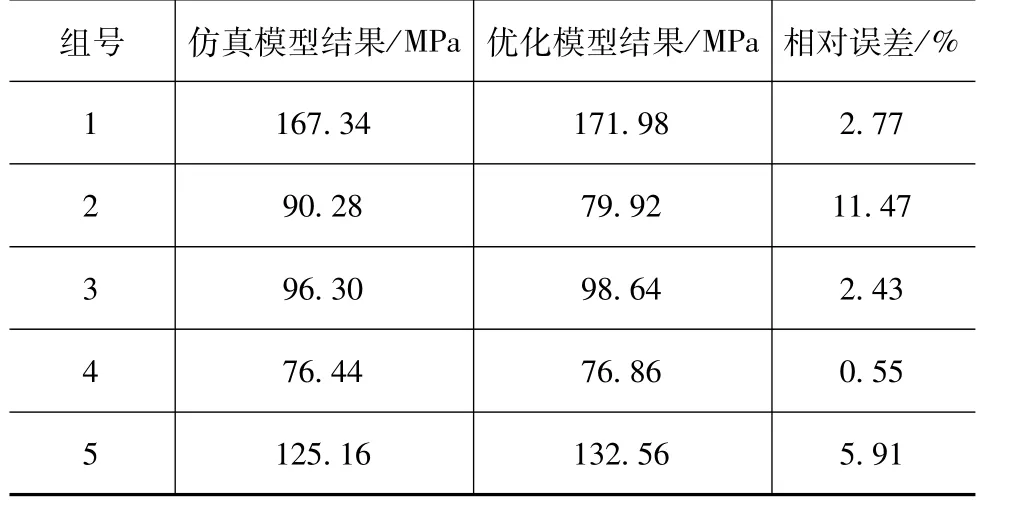
表3 POFP模型

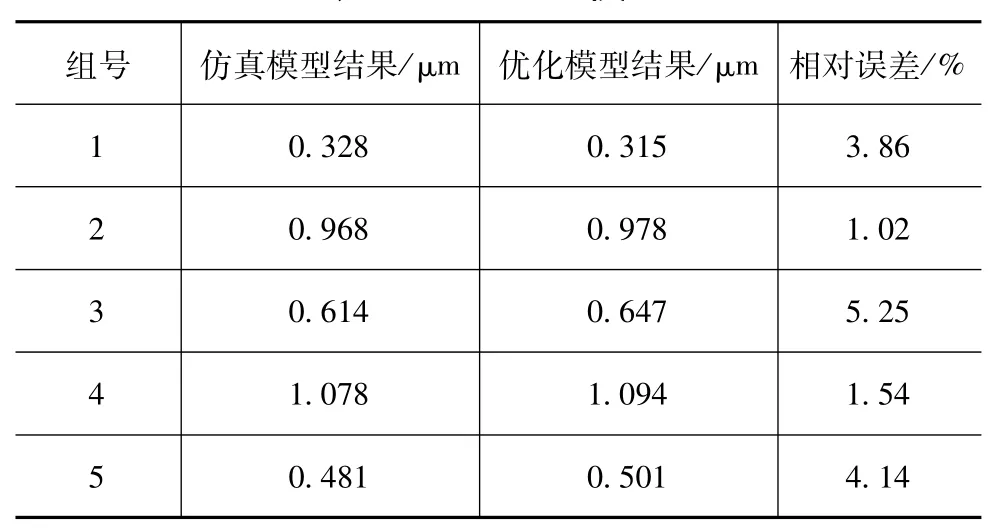
表4 MOFT模型

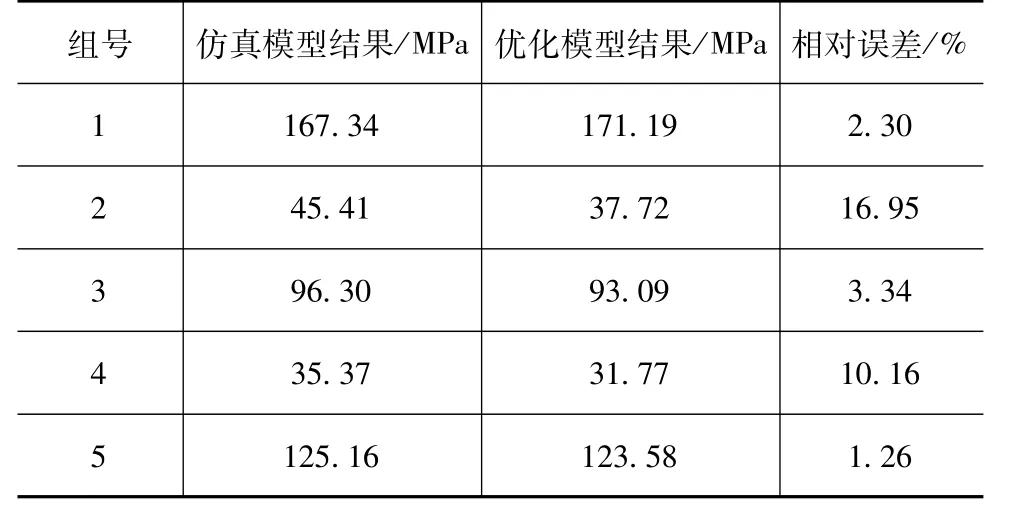
表5 PASP模型

从上面列表中可以看出，各优化模型的预测值与实际仿真结果之间的相对误差较小，说明Kriging方法在较少的采样点的情况下，可以建立较为准确的模型。在优化迭代的过程中，数值模型最优解附近的样本点不断地增加，使得最优解附近的精度得到了很大的提高，因此得到的解更加具有可信性，与理论最优解更接近。

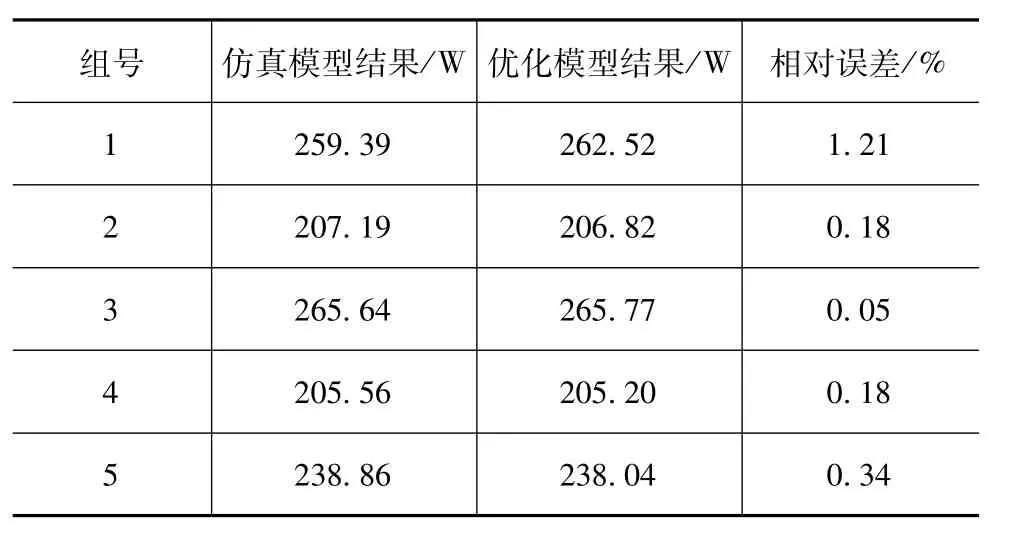
表6 TFPL模型

基于优化模型得到的最优化设计结果如表7所示。

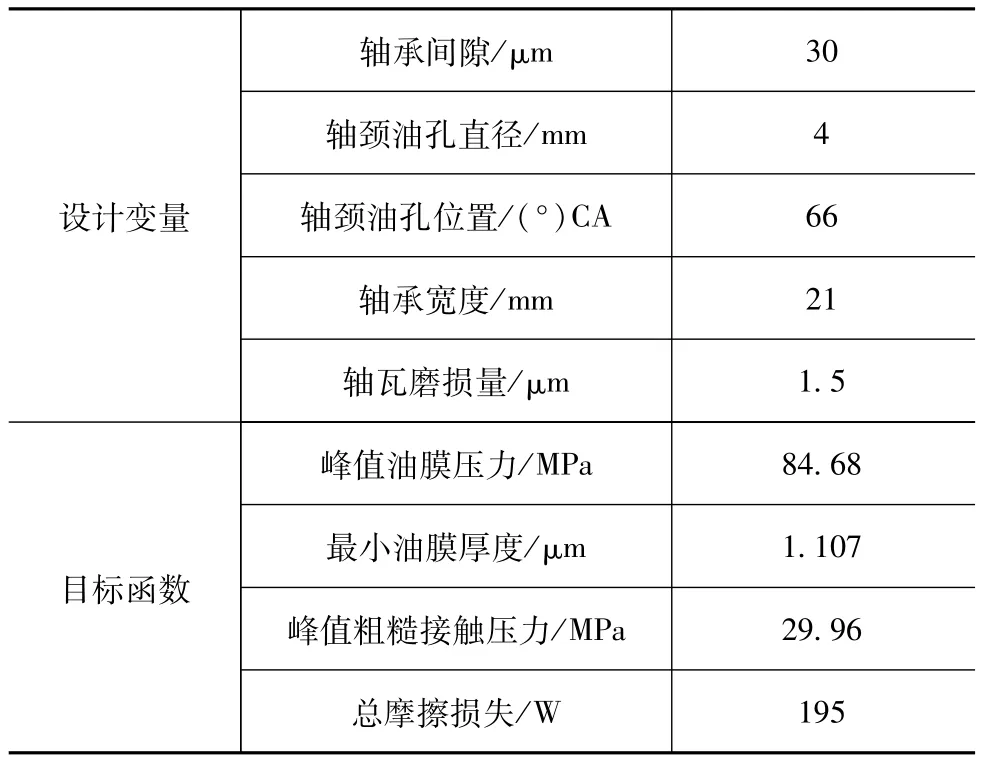
表7 最优设计结果

将优化后的设计变量输入到发动机轴承的实际物理模型中进行计算，以第2主轴承为例，优化前后轴承润滑特性如图3所示。

从图3中可以看出，经过优化后，轴承的最大峰值油膜压力（POPF）由原机的 79.6提高至85.2MPa，但仍满足轴瓦的设计标准；最小油膜厚度（MOFT）由原机的 0.77提高到 1.07μm，提高了39%；最大峰值粗糙接触压力（PASP）由原机的65.8降低至36.2MPa，降低了45%；通过计算得到的平均有效摩擦损失由原机的242.8降低至195.6W，降低了19%，轴承的润滑特性得到明显改善。全转速工况下，曲轴主轴承的总摩擦损失也有明显的下降，如图4所示。

图3 轴承润滑特性优化前后对比

将优化方案应用于实际样机中，进行曲轴摩擦损失测试，结果如图5所示。在测试转速范围内，摩擦损失降低了17.6%，与仿真结果相符。

3 结论

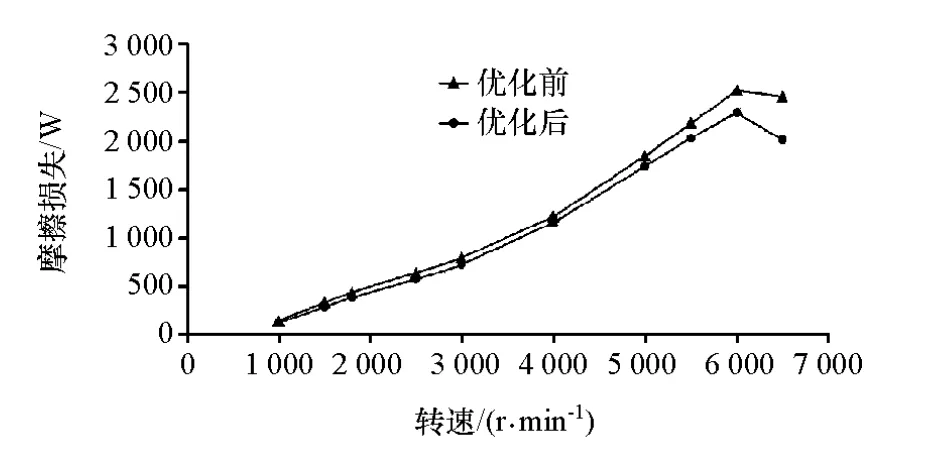
图4 曲轴主轴承摩擦损失仿真结果

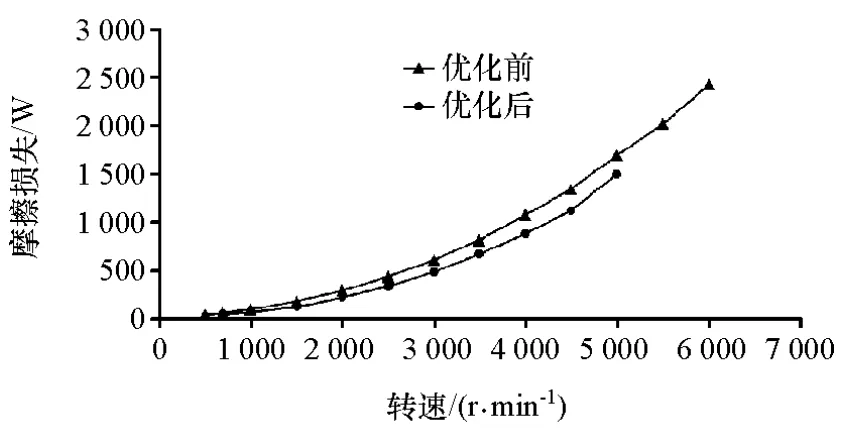
图5 曲轴主轴承摩擦损失试验结果

（1）本文中将全局敏感性分析和PE-HMGE优化算法相结合，研究复杂非线性系统多参数的优化求解问题，提出了多参数多目标优化策略，并将该方法应用到轴承的润滑特性优化设计中。

（2）通过全局敏感性分析方法，定量确定了每个设计参数对润滑特性的影响，从而筛选出重要参数，大大减少了计算量。

（3）本文中提出的模型优化方法在轴承设计中取得良好的优化效果。对比仿真结果，最小油膜厚度提高了39%；最大峰值粗糙接触压力降低了45%；平均有效摩擦损失降低了19%。测试结果也表明轴承的润滑特性得到明显改善，证明了该研究方法的有效性。