基于反步法的自适应神经网络EPS摩擦补偿*

赵林峰，邵文彬，徐飞扬，陈无畏

（1.合肥工业大学汽车与交通工程学院，合肥 230009； 2.安徽江淮汽车集团股份有限公司技术中心，合肥 230601）

前言

电动助力转向系统（electric power steering system，EPS）是当前车辆动力转向系统的理想选择。由于EPS的电机和减速机构所引起的转向系统扰动，造成转向系统动态性能变差和低速回正能力下降，因此，需要采取合适的补偿策略来解决这些问题［1］。EPS的电机补偿分为惯量补偿、阻尼补偿和摩擦补偿3部分，其中摩擦补偿对系统性能影响十分显著。

文献［2］中为改善EPS的动态特性，设计了包括阻尼补偿、惯性补偿和振动抑制在内的补偿控制器。文献［3］中以电机角度为目标，采用滑模观测器对系统的动态性能进行观测和研究，改善了EPS的动态性能。文献［4］中设计了基于模糊PID的电机电流跟踪控制器，实现了电流的精确跟踪，并设计转矩补偿和电机补偿控制策略，改善了EPS动态特性。文献［5］中提出一种动静摩擦转矩共同补偿控制方法，使摩擦补偿转矩在转向盘转动与停止之间平滑过渡。文献［6］中分析了EPS摩擦特性，设计了一种变摩擦补偿控制方法，有效提高了路感反馈强度。

同一款车型、同一套转向管柱的EPS，由于其生产制造工艺的差异和装配的误差，必然造成转向系统的摩擦力矩存在差异，而同一款EPS的控制策略的摩擦补偿策略是固定的，无法对这种个体差异进行补偿，从而造成同一款车型的EPS手感不同，对匹配调试工作带来困难。上述文献虽在EPS补偿方面取得一定效果，但均未对这种个体差异所要求的摩擦力矩补偿进行研究。

本文中在EPS动力学建模的基础上，建立基于LuGre模型的转向系统摩擦模型和摩擦状态观测器。并针对上述个体差异问题，设计一种基于反步法的自适应神经网络控制策略，对EPS的摩擦进行补偿，通过仿真和硬件在环试验验证补偿控制策略的可行性。

1 EPS动力学建模

EPS主要由转向柱、转矩传感器、齿轮齿条、助力电机和电子控制单元（electronic control unit，ECU）等组成，包括输入输出轴、齿轮齿条和助力电机模型，如图1所示。

根据文献［7］建立EPS动力学方程如下。

输入轴和转矩传感器模型：

式中：Td为转向盘转矩；Ts为转矩传感器检测的转矩；Ks为转矩传感器的扭转刚度；Js为转向盘和输入轴总的转动惯量；Bs为输入轴阻尼系数；θs为转向盘转角；θe为输出轴转角。

输出轴模型：

图1 EPS动力学模型

式中：gm为减速机构的减速比；Ta为电机助力转矩；Tp为输出轴作用在齿轮上的转矩；Je为输出轴转动惯量；Be为输出轴的黏性摩擦因数。

在齿轮齿条模型中，将转向柱、电机与减速机构和转向器的摩擦均等效至小齿轮处。

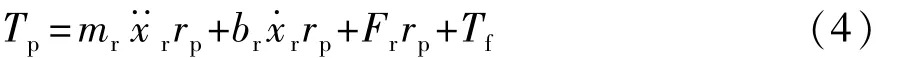
式中：Tf为转向系统等效摩擦力矩；Fr为转向机构对齿轮齿条反向拉力；rp为小齿轮节圆半径；mr为齿条质量；xr为齿条位移；br为齿轮齿条阻尼系数。

助力电机模型：

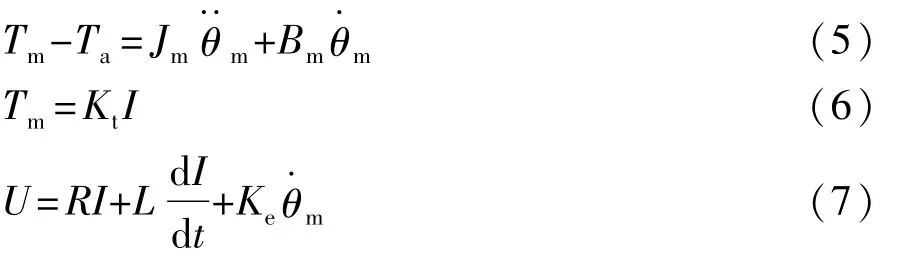
式中：Tm为电机电磁转矩；Jm为电机转动惯量；Bm为电机阻尼系数；θm为助力电机转角；Kt为电机转矩系数；U为电枢电压；R为电枢电阻；I为电枢电流；L为电枢电感；Ke为反电动势系数。

利用CarSim软件中的整车模型，搭建CarSim与Simulink联合仿真平台，如图2所示。在CarSim中，进行整车参数、外部环境和工况的设置。在联合仿真模型中，EPS模型输出的左、右前轮转角作为Car-Sim整车模型的输入，而CarSim整车模型输出的左、右前轮回正力矩则作为EPS模型的输入。

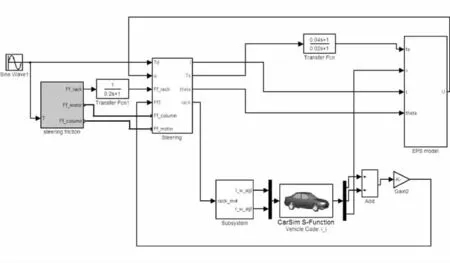
图2 CarSim与Simulink联合仿真模型

2 转向系统摩擦建模

摩擦补偿方法主要分为两大类：基于摩擦模型的补偿方法和不基于摩擦模型的补偿方法。其中，基于摩擦模型的补偿方法得到了广泛应用，为确保补偿更加精确，关键在于建立适当的摩擦模型。多年来，经过学者们的不断研究，从静态模型到动态模型，先后提出几十种摩擦模型，其中LuGre模型能最准确地描述机械伺服系统中的摩擦特性，因此应用最为广泛［8］。随着智能控制的发展，针对摩擦所具有的不确定性，基于摩擦模型的补偿方法又分为固定补偿和自适应智能补偿［9］。目前，基于智能控制的自适应摩擦补偿方法已被运用到各个领域，并取得了一定的成果，即通过模糊和神经网络等智能控制来逼近摩擦的不确定项，并结合各种控制方法对摩擦进行补偿。

综上所述，本文中采用LuGre模型建立转向系统摩擦模型并设计了摩擦状态观测器和基于反步法的摩擦补偿自适应控制器。

2.1 基于LuGre模型的摩擦建模

LuGre模型是以各种平均行为来建模的，并考虑了库伦摩擦、Stribeck负斜率效应和摩擦记忆等现象，能比较准确地描述系统摩擦的静态和动态特性。该模型对系统动态摩擦的描述采用的是鬃毛概念，即将系统的接触面等效为大量具有随机行为的弹性鬃毛，由于鬃毛的变形而产生摩擦力，如图3所示。

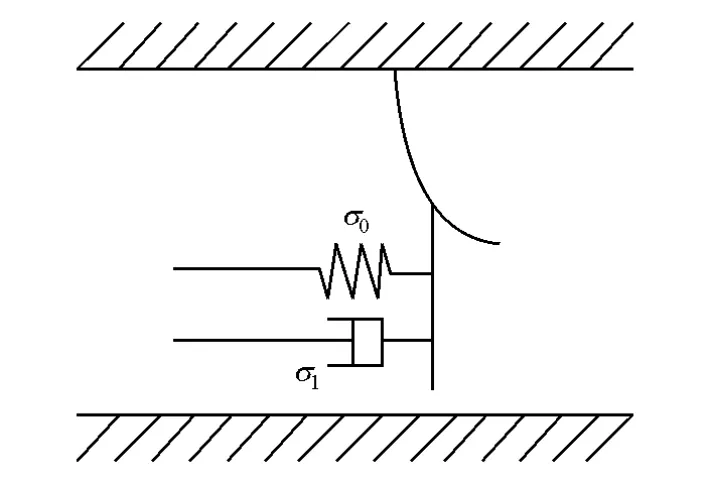
图3 LuGre摩擦模型示意图

由于转向系统中的摩擦为动态摩擦，十分复杂，因此，本文中采用LuGre模型对转向系统进行摩擦建模。

转向系统的LuGre模型为

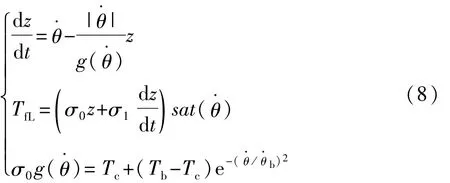
式中：TfL为转向系统LuGre摩擦力矩；θ·为接触面相对转速；σ0为鬃毛平均刚度；σ1为鬃毛平均阻尼系数；Tc为库伦摩擦力矩；Tb为最大静摩擦力矩；θ·b为Stribeck临界转速；z为接触面鬃毛的平均变形量；sat（·）为临界函数，阈值限制为±1。

由于制造和装配引起的个体化摩擦力矩差异很小且不确定，用Tfr表示。本文中采用自行开发的转向硬件在环试验台进行试验测定，选取5套同型号管柱，采用转向机器人在同样的条件下多次试验，测得Tfr约在0.1～1N·m范围以内，在仿真中使用随机函数来模拟该力矩差异。将全部摩擦力矩等效至转向小齿轮处，则转向系统摩擦模型为

2.2 摩擦观测器设计

在设计控制策略前，须先已知摩擦模型各参数，LuGre模型中的未知参数均可测［10］。由于状态变量z无法测量，故本文中采用非线性状态观测器对z进行实时估计，根据式（8）LuGre模型可得状态观测器方程为

3 摩擦补偿控制策略设计

一般来说，EPS系统根据车速和转矩确定基本助力电流Ip，另外考虑到阻尼和惯性等因素确定其它补偿电流Io，本文中主要对摩擦补偿电流Ic进行研究。传统的摩擦补偿方法均为输出一个与摩擦力矩成比例的定值补偿电流，称为定摩擦补偿电流。但未考虑到摩擦的非线性、负载的不确定性和上述个体差异对EPS系统性能和匹配调试的影响。本文中在神经网络逼近系统的基础上，设计一种基于反步法的自适应摩擦补偿控制策略对EPS摩擦进行在线补偿，使EPS的电机电流跟踪精度更高、动态性能更好。EPS摩擦补偿控制策略总体框图如图4所示。

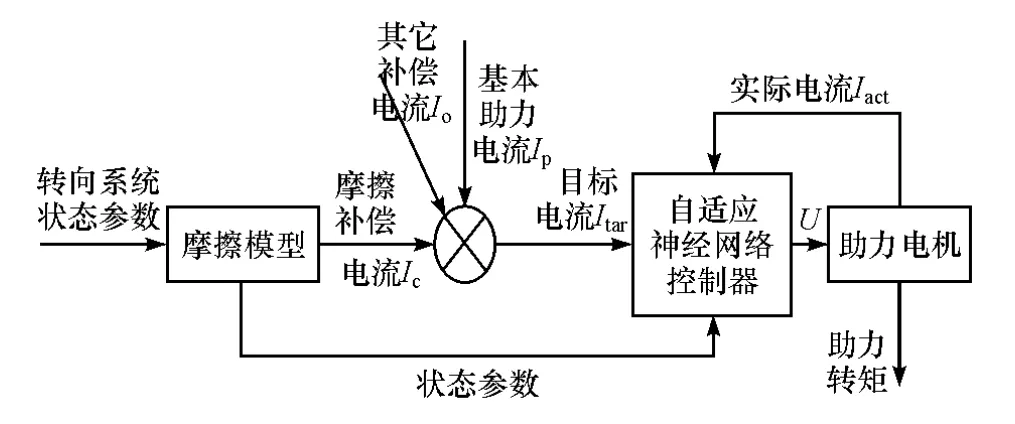
图4 摩擦补偿控制策略总体框图

3.1 径向基神经网络

近年来，神经网络控制已广泛应用于机电伺服系统的非线性摩擦补偿中［11-12］。径向基（radial basis function，RBF）神经网络在文献［13］中已证明其可高精度地逼近任意连续函数，具有任意逼近的特性。因此采用RBF神经网络函数对EPS中的非线性外部扰动和个体差异造成的摩擦力矩波动进行逼近，其结构如图5所示。其中，网络的输入量为电机实际电流与目标电流的偏差及其导数，输出量为未知的非线性外部摩擦力矩。为获取训练神经网络所需数据，首先建立EPS参考模型，设计电流跟踪PID控制器，再随机生成大小不同的外部干扰摩擦力矩进行多次仿真，并保存大量的输入输出数据应用于训练网络。图5还给出了训练神经网络时网络输出误差的变化曲线，随着迭代次数的增加不断减小误差，最终网络的逼近误差接近为零。

RBF神经网络算法为

式中：x为神经网络的输入信号；i为输入信号个数；j为隐含层节点；h为径向量为j节点的高斯基函数输出；bj为j节点的基宽度参数；cj为j节点的中心矢量；w为神经网络权值；ε为神经网络逼近误差。

3.2 摩擦补偿控制器设计

反步法是一种递归算法，将李亚普诺夫函数的选取与控制器设计相结合，从最低阶次微分方程开始，引入虚拟控制的概念，然后逐步设计满足要求的虚拟控制，最终设计出真正的控制律。反步法的最大优点在于它不会消除有用的非线性，而是具有灵活性，以跟踪和镇定为目标，而非追求线性化。在机械伺服系统摩擦补偿方面，反步法是最常用的一种方法［14］。

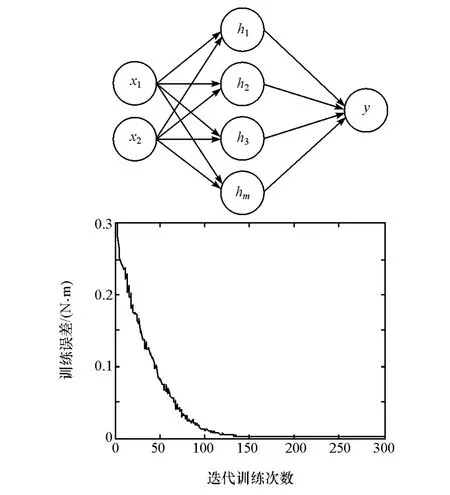
图5 RBF神经网络的结构与训练误差曲线

基于反步法设计了一种自适应神经网络控制器，通过RBF神经系统逼近非线性扰动，不仅可简化控制器设计过程，且能抑制摩擦等非线性因素的影响，提升系统跟踪性能。采用反步法的标准流程来设计控制器，其具体方法如下。

步骤1：定义EPS助力电机电流跟踪误差

式中：Itar为无扰动理想目标电流；Iact为电机实际电流。

对式（12）求导，可得电流跟踪误差的导数为

定义Lyapunov函数：

求导可得

式中：c1＞0，c2＞0。取虚拟控制：

则

步骤2：重新定义Lyapunov函数

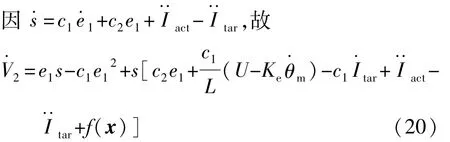
式中：w*为理想逼近参数为估计逼近参数；ε为最小逼近误差；e为神经系统的输入向量，e=［e1e·1］T。

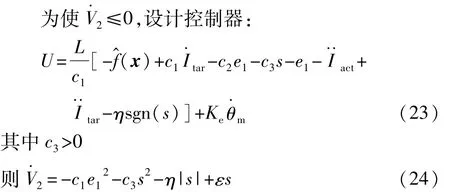
3.3 稳定性分析

定理1 为保证自适应神经闭环系统的稳定，须设置参数的自适应律：

式中Γ为学习速率。

证明：设定Lyapunov函数：

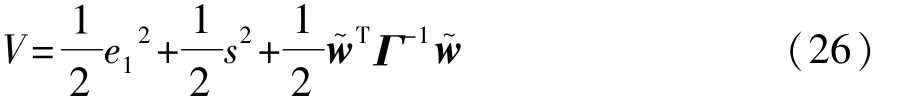
将式（13）、式（20）和式（23）代入得

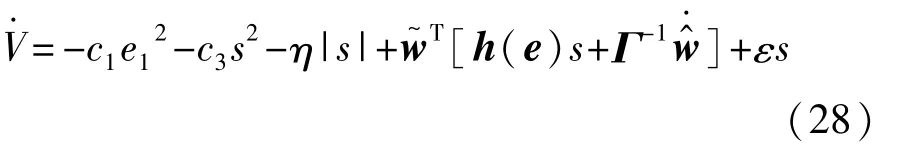
将式（25）参数自适应率代入，可得

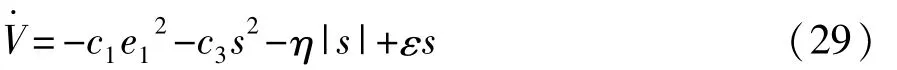
4 仿真与试验验证

4.1 仿真分析

在MATLAB／Simulink环境中搭建基于LuGre摩擦模型的EPS仿真模型，仿真参数如表1所示。

表1 仿真参数

首先进行电流跟踪性能的验证，依次输入10，20和30A的阶跃目标电流，时间间隔为2ms，分别采取模糊PID控制和自适应神经网络控制对其进行跟踪，仿真结果如图6（a）所示，电流跟踪误差如图6（b）所示。从图中可以看出，自适应神经网络控制能比模糊PID控制更快速稳定地跟踪上目标电流，且误差几乎趋近于零，说明自适应神经网络控制的跟踪性能比模糊PID控制更优越，能使系统的动态性能得到很大的提升。

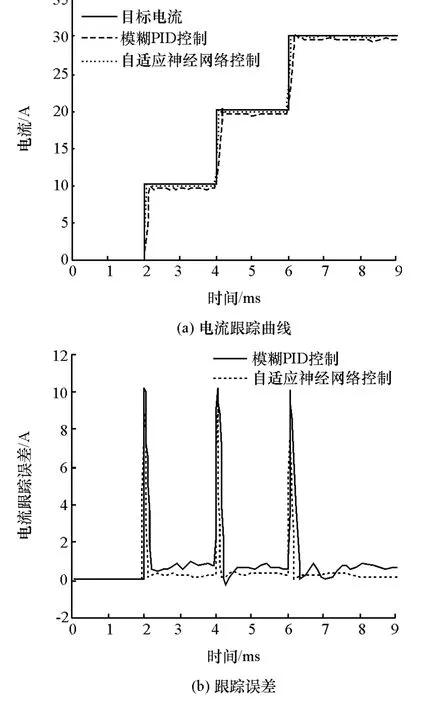
图6 目标电流跟踪结果对比图

然后进行转向轻便性仿真。将车速设置为10km／h，选取双纽线工况，观察摩擦补偿前后转向盘转矩随转角变化的趋势，结果如图7所示。从图中可以看出，加入摩擦补偿后，转向盘上所需施加的转矩明显减小，转向轻便性得到改善，补偿效果明显。且与传统的定摩擦补偿控制相比，自适应神经网络摩擦补偿控制策略可明显抑制因摩擦不确定性引起的转向盘转矩波动，且转向盘操纵转矩更小，表现出更加良好的补偿效果。

图7 轻便性仿真转向盘转角转矩图

转向系统内部的摩擦也会在一定程度上影响回正性能，因此下面进行回正性能仿真。将车速设置为30km／h，转向盘初始输入转角为160°，待汽车行驶稳定后，撤消输入力矩，使汽车进入撒手回正状态，观察回正时间和回正残余角，仿真结果如图8所示。从图中可以看出，加入摩擦补偿控制后，转向盘的回正速度变快，回正残余角变小，即EPS在加入补偿控制后，对回正时的摩擦力矩进行了很好的补偿，回正性能得到改善。且与传统的定摩擦补偿控制策略相比，自适应神经网络控制的回正时间更短，回正残余角更小，回正性能更佳。

图8 回正仿真转向盘转角变化图

4.2 硬件在环试验

为进一步验证上述摩擦模型和补偿算法的有效性，搭建了EPS硬件在环试验台，主要由试验台架、转向管柱、伺服电机、转矩转角传感器、转向机器人、EPS控制器、工控机、PXI主机和数据采集卡等组成，如图9所示。

图9 EPS硬件在环试验台

首先选取与仿真相同的工况，进行转向轻便性试验，结果如图10所示。从图中可以看出，转向盘操纵转矩随转角变化的趋势与仿真结果一致，补偿后的转向盘转矩减小，说明转向轻便性得到了一定的改善，且采用本文的控制策略后，转矩下降更明显，补偿效果更好。同时，与传统的定摩擦补偿控制策略相比，补偿后转矩抖动明显减弱，转向盘操纵手感大为改善，证明了自适应神经网络摩擦补偿控制策略可对摩擦的非线性、不确定性和个体差异进行更好的补偿。

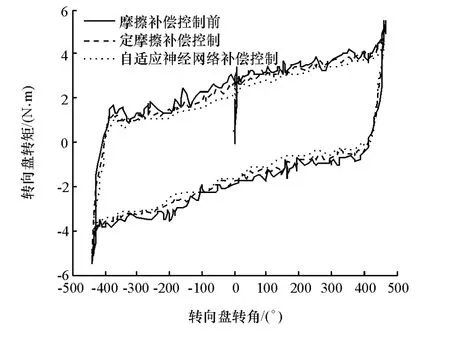
图10 轻便性试验转向盘转角转矩图

然后进行回正性能试验，设定车速为30km／h，初始转向盘转角输入为160°，待汽车行驶稳定后，松开转向盘，使汽车进入撒手回正状态，记录回正时间和回正残余角的变化，试验结果如图11所示。从图中可以看出，补偿后的回正时间明显缩短，回正残余角大为减小，回正性能得到提升。且采用自适应神经网络补偿控制策略后，回正时间更短，回正残余角趋近于零，回正性能更好。

5 结论

（1）在EPS动力学模型的基础上，建立了基于LuGre模型的转向系统摩擦模型和摩擦状态观测器，并针对摩擦的非线性扰动和个体化差异问题，在模型中加入了随机扰动变量。

图11 回正试验转向盘转角变化图

（2）设计了基于反步法的自适应神经网络摩擦补偿控制策略，通过Lyapunov稳定定理证明闭环系统是稳定的，并与模糊PID控制进行比较，证明了其电流跟踪性能更加优越。

（3）最后进行仿真和硬件在环试验，结果表明：与传统的定摩擦补偿控制策略相比，基于反步法的自适应神经网络摩擦补偿控制策略可使EPS具有更加良好的动态特性、转向轻便性和回正性能。