3.2.1古典概型

辽宁省抚顺德才高级中学 郑 丹

教学目标：1.理解古典概型及其概率计算公式。

2.会用列举法计算一些随机事件所含的基本事件数及事件发生的概率。

教学重点：理解古典概型的概念及利用古典概型求解随机事件的概率。

教学难点：判断一个试验是否为古典概型，分清在一个古典概型中某随机事件包含的基本事件的个数和试验中基本事件的总数。

教材分析：根据本节课的特点，采用引导发现和归纳总结相结合的教学方法，通过提出问题、思考问题、解决问题等教学过程，观察对比、概括归纳古典概型的概念及其概率公式，再通过具体问题的提出和解决，来激发学生的学习兴趣，调动学生的主体能动性，让每一个学生充分地参与到学习活动中来。

学情分析：

我所带班级的学生思维活跃,但对基本概念重视不足,对知识深入理解不够。善于发现具体事件中的共同点及区别,但从感性认识上升到理性认识有待提高

教学准备：PPT课件、硬币、骰子、教案、学案、小卷

教学过程：

课前,教师布置任务,以数学小组为单位完成模拟试验

试验一:抛掷一枚质地均匀的硬币,分别记“正面朝上”和“反面朝上”的

数学小组至少完成20次(最好是整十数),最后由科代表汇总

试验二:抛掷一枚质地均匀的骰子,分别记录：“1点”“2点”“3点”“4点”“5点”和“6点”的次数,要求每个数学小组至少完成60次。

试验三:从数字1，2，3，4中任意取出两个不同的数字的试验中,有几个基本事件?分别是？

试验四:若将上面的抽取方式改为按先后顺序依次抽取,结果如何呢

教师最后汇总方法、结果和感受,并提出问题。

1.用模拟试验的方法来求某一随机事件的概率好不好?为什么?

不好,要求出某一随机事件的概率,需要进行大量的试验,并且求出来的结果是频率,而不是概率

2.根据以前的学习,上述两个模拟试验的结果之间都有什么特点？

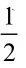
板演：上述试验中的随机事件称为基本事件,它是试验的每一个可能结果。

基本事件有如下的两个特点：

(1)任何两个基本事件是互斥的

(2)任何事件(除不可能事件)都可以表示成基本事件的和。

特点(2)的理解:在试验一中,必然事件由基本事件“正面朝上”、“反面朝上”组成;在试验二中,随机事件“出现偶数点”可以由基本事件“2点”“4点”和“6点”共同组成。

练习从数字1，2，3，4中任意取出两个不同数字的试验中,有哪些基本事件？

分析:为了解基本事件,我们可以按照字典排序的顺序,把所有可能的结果都列出来。利用树状图可以将它们之间的关系列出来。

我们一般用列举法列出所有基本事件的结果,画树状图是列举法的基本方法,一般分布完成的结果(两步以上)可以用树状图进行列举。

解:所求的基本事件共有6个

A={1,2},B={1,3},C={1,4} D={2,3},E={2,4},F={3,4}

观察对比,发现两个模拟试验和例1的共同特点:

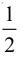
试验二中所有可能出现的基本事件有“1点”“2点”“3点”“4点”“5点”和“6点”6个并且每个基本事件出现的可能性相等,都是

练习中所有可能出现的基本事件有“A”“B”“C”“D”“E”和“F”6个,并且每个基本事件出现的可能性相等,都是经概括总结后得到:

(1)试验中所有可能出现的基本事件只有有限个;(有限性)

(2)每个基本事件出现的可能性相等。(等可能性)

我们将具有这两个特点的概率模型称为古典概率概型,简称古典概型。

问题思考：在古典概型下，基本事件出现的概率是多少？随机事件出现的概率如何计算？

分析：

实验一中，出现正面朝上的概率与反面朝上的概率相等，即P(“正面朝上”)= P(“反面朝上”)

有概率的加法公式得P(“正面朝上”)+P(“反面朝上”)=1

实验二中，出现各个点的概率相等，即P(“1点”)=P(“2点”)=P(“3点”)=P(“4点”)=P(“5点”)=P(“6点”)反复利用概率的加法公式，得出：P(“1点”)+P(“2点”)+P(“3点”)+P(“4点”)+P(“5点”)+P(“6点”)=1

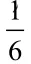
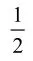
根据上述两则模拟实验，可以概括总结出，古典概型计算任何事件的概率计算公式为：

小结提问：在使用古典概型的概率公式时，应该注意什么问题？

答：（1）要判断该概率模型是不是古典概型；

（2）要找出随机事件A包含的基本事件个数和试验中基本事件的总数。

1.我们将具有

(1)试验中所有可能出现的基本事件只有有限个;(有限性)

(2)每个基本事件出现的可能性相等。(等可能性)

这样两个特点的概率模型称为古典概率概型,简称古典概型。

2.古典概型计算任何事件的概率计算公式

3.求某个随机事件A包含的基本事件的个数和实验中基本事件的总数的常用方法是列举法(画树图和列表):应做到不重不漏。