一种改进的DME/DME导航台优化算法

石潇竹，李贺，胡杰

（1 空中交通管理系统与技术国家重点实验室，南京 210007；2 中国电子科技集团公司第二十八研究所，南京 210007）

0 引言

陆基导航系统是目前民航领域最通用的一种导航方式。通过在飞机的飞行航路上设置若干个地面导航台，陆基导航系统根据导航台信号，引导飞机在飞行过程中实现台对台飞行，当到达机场上空之后，飞机再依靠仪表着陆系统引导着陆[1]。由此可见，在整个飞行区间，导航台与飞机之间相关信息（如飞机的位置、高度、速度等）的准确度至关重要。

陆基导航系统主要有测角和测距两种定位手段，分别由 VOR（Very high frequency omni directional range）和 DME（Distance Measuring Equipment）两种导航系统来实现。

DME系统由地面测距信标台和机载接收机两部分组成，采用无线电询问-应答的工作方式来测量飞行器与地面导航台站之间的斜距。由于单一的陆基导航台站无法实现对飞行器的定位，因此陆基导航可采用VOR/DME组合或DME/DME组合的方式来实现飞行器的定位。

DME/DME定位方式是利用两个或两个以上DME测得飞机到导航台的距离，并利用地面DME台的位置来实现飞行器的定位。而飞行器在飞行过程中，通常是在多个地面导航台的覆盖范围内，飞行器能得到自身与多个导航台之间的测距信息，而每个测距信息的精度又不尽相同，因此在定位过程中，飞行器对导航台站的选择和切换变得至关重要[2]。

为应对空中交通的日益繁忙，国际民航组织也提出了基于性能导航（performance based navigation，PBN）的概念，其目的是为了缩短航路间隔，提高空域利用率并降低成本。PBN包括两类基本导航规范：区域导航（area navigation，RNAV）和所需导航性能 （required navigation performance，RNP）[3][4][5]。RNAV可以使飞机在相关导航设施的信号覆盖范围内，或在机载自主导航设备能力限度内，或在两者配合下沿所需的航路飞行。而 RNP则限定了飞机在安全有效运行条件下对导航系统的水平方向定位误差要求。

随着用户对DME的测距精度和可靠性提出更高要求，研究导航台测距精度和优化选择算法显得具有非常重要的意义。许多文献已经针对DME/DME测距展开了研究，如文献6分析了影响DME测距精度的原因，文献 7和文献 8研究了RNAV中DME/DME的测量精度，在文献9中，作者提出了一种航路导航性能评估方法，文献 10结合民用航空飞行管理系统，分析了陆基导航系统的定位误差，但这些方法都没有针对误差提出改正措施；文献10根据DME测距精度，研究了 RNAV中导航台的选择算法，但该选择算法没有考虑导航台跳变所带来的测距不准确问题。

为此，本文针对DME/DME系统中导航台切换频繁导致的测距不准确问题，提出了一种新的导航台优选算法。首先根据DME/DME导航方式给出了水平方向定位误差标准差的计算方法，然后以A593航路为例，用 MATLAB软件仿真了基于最小定位误差准则下的DME导航台选择算法，接着提出一种新的导航台优选算法。通过对两种算法的选台结果进行分析比较，证明提出的导航台优选算法能够选出一对更加合理的 DME信标台，从而满足DME/DME区域导航精度要求，提高选台算法的连续性。

1 水平方向定位标准差

水平方向定位误差表示飞机实际位置与飞机管理计算机（FMC）估计位置之间的误差。它主要取决于信标台距离测量误差和信标台的几何分布，因此在信标台测距误差确定的情况下，根据一定的计算准则，选择相对于飞机位置几何分布最好的一对DME信标台进行DME/DME方式定位，可以尽可能的减小水平定位误差，得到最优的导航性能。

1.1 DME测量误差

RNP区域导航计算中设定DME斜距测量误差满足均值为0的高斯分布。斜距测量误差的标准差计算公式如下：

式中，L为飞机与信标台的斜距（n mile）。

1.2 DME/DME定位误差区域

单独的DME系统只能测得飞机与DME台之间的斜距，当采用两套DME系统同时为飞机提供距离信息时，再结合地面DME的位置信息，就能够完成飞机的定位导航任务。由两套或两套以上DME系统组成的导航系统称为DME/DME系统。如果没有测量误差存在，两个DME信标台可以精确定位到飞机的位置（即两条距离线的交点），而由于DME系统水平测量误差的存在，使得实际定位过程中得到的定位结果位于图1所示的四边形定位误差区域内[12]。

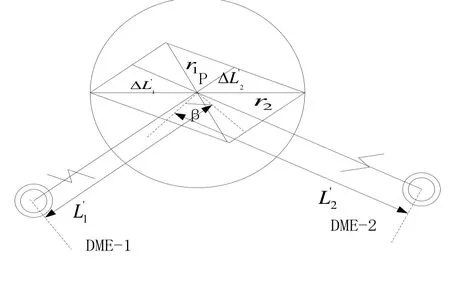
图1 定位误差区域示意图

1.3 水平方向定位标准差计算

定位误差Δs与两条位置线误差之间关系的示意图如图2所示。

根据余弦定理可得：

式中，ϕ′为两条位置线的夹角。

因为Δu和Δv是零均值随机变量，Δs也是随机变量，它的方差由式（3）确定：

式中，ρ是两位置线误差的相关系数。

图2 两条误差线示意图

由于两个DME接收机独立工作，因此位置线误差的相关系数为 0，可以得到水平方向定位标准差为：

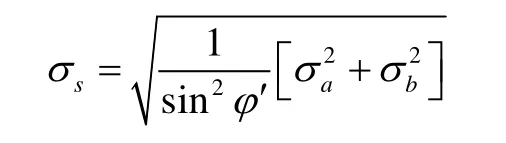
2 基于最小定位误差的导航台选择算法

2.1 DME/DME区域导航要求

DME是靠测量飞行器与导航台之间的距离来进行定位导航的，其测量精度与距离有关。ICAO发布的基于性能导航的手册对参与 PBN导航的DME有着明确规定：DME台到飞机的距离大于160n mile 和小于3n mile的DME均不可可用，也即：如果航路点到各DME的水平距离L满足

则该DME可用于DME/DME区域导航。

DME/DME进行区域导航时，飞机通过2台或更多的DME的交角计算其位置，如果仅能接收2台DME的输入，那么飞机和DME对构成的夹角必须在30°～150°之间，此时的两个DME被称为有效DME对[13]。

2.2 DME/DME导航台选择算法

文献 14提出了一种基于最小定位误差的导航台选择算法。其算法实现流程主要为：

（1）在WGS-84坐标系下利用导航数据库的信息计算飞机到两个DME台的斜距，通过飞机的已知高度，计算出飞机与DME台的水平距离，对飞机到台距离进行判断，确定飞机处在DME覆盖区并满足距离条件3～160N MILE。

（2）根据余弦定理计算出水平面上飞机投影与两个导航台连线的夹角，对夹角进行判断，保证夹角在30°到150°，确保飞机处在DME对的有效覆盖区域，筛选得到候选DME对。

（3）计算候选DME对定位误差的标准差，选择定位误差最小的DME对进行导航。

这种方法通过在任一航段上选择定位误差最小的DME对进行定位导航，可以使导航精度在理论上达到最优，但这种方法没有考虑到每对导航台站的有效导航范围。如果在某段航路上存在有多个有效导航台，则可能会出现参与导航的DME对频繁跳变的问题，从而导致换台过于频繁，定位精度变得不稳定。

3 改进的导航台优选算法

针对导航台站选择中的切换频繁问题，本文提出一种优化的导航台选择算法。该方法首先采用基于最小定位误差的导航台选择方法选出DME对，然后通过设定一个阈值来判定是否需要切换导航台。

所需性能导航的类型分为多种，其中RNP-4类型指以计划航迹为中心，侧向（水平）宽度为±4海里的航路。RNP-4有较松的航路宽度要求，适应于目前陆基航行系统支持的空域环境。

对于满足RNP-4导航要求的航路，设定阈值为2n mile，当上一个航路点所选DME对在当前航路的定位误差的标准差小于阈值，则不切换信标台；同时要考虑连续三个航路点导航台切换两次的情况，当上一个航路点所选DME对在当前航路点不满足区域导航要求，则必须切换DME信标对，此时应该综合考虑下一个航路点的DME选择结果，在满足导航性能的要求下，合理选择当前航路点的DME信标对。

其实现流程图如图3所示。

图3 优化的导航台选择算法流程图

具体的实现过程如下：

（1）首先计算出飞机与DME台的水平距离，对飞机与导航台之间的距离进行判断，确定飞机处在DME覆盖区并满足距离条件3～160n mile。

（2）计算出水平面上飞机投影与两个导航台连线的夹角，保证夹角在30°到150°，确保飞机处在DME对的有效覆盖区域，筛选得到候选DME对。

（3）计算候选DME对的定位标准差，得到定位误差最小的DME对。

（4）计算上一个航路点所选DME对在当前航路点的定位标准差，如果该值小于阈值，则不切换信标对。

（5）如果该值大于阈值，则计算当前航路点定位误差最小的DME对在下一个航路点的定位标准差，如果小于阈值，当前航路点选择当前航路点定位误差最小的DME对。

（6）如果大于阈值，则考虑下一个航路点的定位误差最小的DME对在当前航路点是否可用，如果可用，当前航路点选择下一个航路点定位误差最小的DME对。

（7）如果不可用，则当前航路点选择当前航路点定位误差最小的DME对。

这里提出的改进的导航台选择算法能够在满足RNP-4区域导航性能要求的前提下，最大限度的减小了导航台的切换次数，并且计算复杂度低，有很强的实用性。

4 仿真实验

本节通过对A593航路进行分析来验证提出的改进的选择算法。利用航路图上航路区的 12个航路点坐标和周围的DME信标台坐标数据，假设飞机每次沿着航路飞行，忽略实际飞行过程中的航迹偏移，对 12个离散的航路点进行分段线性插值，得到11个航路段，每个航路段有20个航路点，从而得到航线上的221个内插航路点坐标，并依次编号为 1-221，飞行高度取 6000m。计算统一采用WGS-84坐标系。

A593航线及其周围信标台分布示意图如图4所示。

4.1 基于最小定位误差的导航台选择算法性能

首先，计算出每个航路点选择DME信标对的水平方向定位误差标准差，其结果示意图如图5。

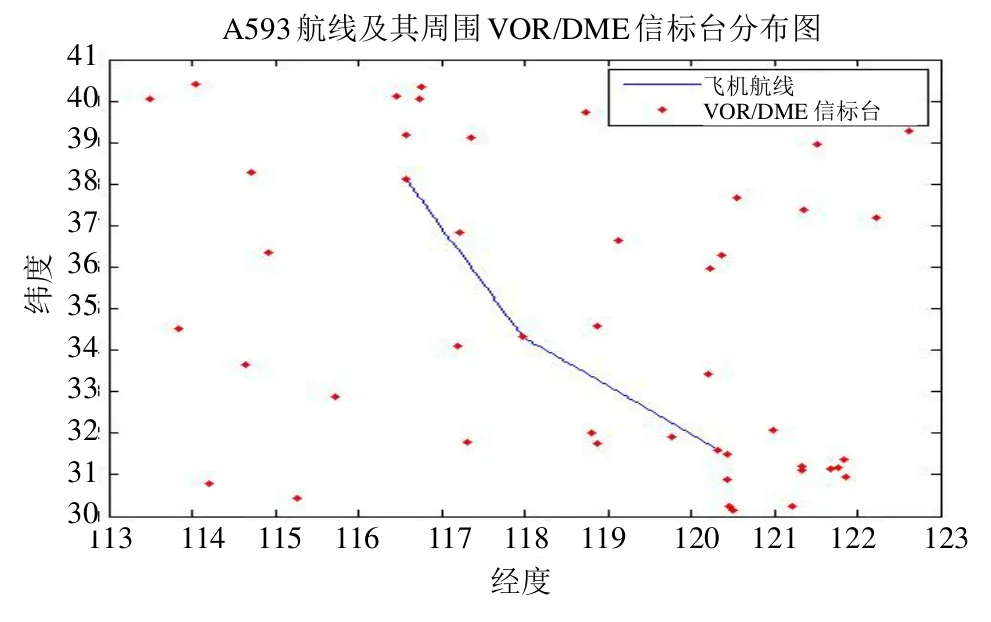
图4 A593航线及其周围信标台分布示意图

图5 各个航路点信标对的水平方向定位误差标准差

从图5可知：A593航线的航路点所选DME信标对水平方向定位误差均小于2海里，满足区域导航RNP-4的要求。然后，计算出每个航路段的导航台切换次数，其示意图如图6所示。

图6 各个航路段的导航台切换次数示意图

从图6可知：A593航路飞行过程中总共切换台站20次，切换频率比较高，尤其在第7航段，每个航路段均是20个航路点，切换频率达到了25%。

4.2 改进的导航台选择算法性能

首先，计算出每个航路点选择DME信标对的水平方向定位误差标准差，其结果示意图如图7所示。

图7 优化选择算法的水平方向定位误差标准差

从图7可知：改进选台算法下，A593航路所选DME信标对水平方向定位误差均小于2海里，仍然满足区域导航RNP-4的要求。

然后，计算出每个航路段的导航台切换次数，如图8所示。

图8 优化选择算法的导航台切换次数示意图

从图8可以看出：A593航路飞行过程中总共切换台站9次，导航连续性得到了很大的改善，每个航路段中20个航路点导航台最多切换3次，满足连续性的要求。

4.3 两种导航台选择算法仿真结果对比

（1）两种算法下导航台选择结果对比图如图9所示。

对比图9（a）和（b）可以看出:利用改进的导航台选择算法得到的结果中，有较多的一个 DME导航台周围出现连续连线的情况，这种情况出现的越多，说明航路上导航台切换的次数越少，进一步证明了该算法的有效性。

（2）两种算法下导航台切换情况对比图如图10所示。

图9 两种算法下导航台选择结果对比图

图10 两种算法下导航台切换情况对比图

由图10可知：传统选台算法在编号为80-160的航路点组成的航路区出现了频繁切换导航台的现象，80个航路点切换了9次导航台，并且存在相邻航路点切换2次的情况，严重影响了导航的连续性；采用改进的选台算法后，该航路段仅切换了 2次，并且没有相邻航路点连续切换导航台的现象，进一步说明改进算法在很大程度上提高了本段航路导航台选择的稳定性。

5 总结

本文针对传统导航台选择算法中的导航台频繁切换问题，在满足区域导航性能要求的前提下，提出了一种改进的DME/DME导航台选择算法。该算法首先基于最小定位误差准则选出DME对，然后计算上一个航路点所选DME对在当前航路的定位误差的标准差，通过比较定位误差的标准差是否大于阈值来判断是否需要切换导航台。论文以A593航路为例，通过建立导航台自动选择模型，对对所选DME/DME区域导航性能进行仿真验证。仿真结果表明：在飞机的航路点位置及航路周围的 DME导航台分布一定的情况下，该算法能够自动选择具有更高精度的导航台，从而满足DME/DME区域导航的性能要求，提高了导航的连续性，在地面导航台分布密集的地区，该算法具有更加实用的价值。