基于改进遗传算法的管道机器人摩擦参数辨识
刘 鹏,赵言正,闫维新
(上海交通大学机器人所,上海 200240)
摩擦广泛存在于工业生产中,研究机器的摩擦特性对于机器性能和生产效率的提高具有不可忽略的意义。以一种用于管道槽口宽度检测的机器人为研究对象,其主要由侧壁支撑挡板、检测装置、电缆卸扣、橡胶履带、刮油板、夹紧装置、电控盒以及动力机构构成,如图1所示。管道机器人受到的摩擦力主要存在于橡胶履带与特种钢壁面、刮油板与特种钢壁面以及电缆与特种钢壁面之间。多油潮湿的工作环境,使得机器人在运行过程中存在严重磨损,探讨其摩擦力可以为进一步研究提供参考。

图1 管道槽口检测机器人Fig.1 Robot for detecting pipe notch
1 研究方法
摩擦模型分为静态摩擦模型和动态摩擦模型。适合的摩擦模型可以准确描述机器人的运动特性以及环境因素等对机器人所受摩擦力的影响。孙洪鑫等[1]采用改进遗传算法辨识LuGre模型参数,利用伺服系统输出的位移和控制力直接进行参数辨识,虽然辨识速度较快,但精度较低。林朝安[2]基于能量法则将参数辨识问题转化为参数优化问题,提出一种改进后的遗传算法,并设计实验方案验证,但算法所采用的算子取值不变,易造成局部收敛现象。Alonge等[3]以定子电压、定子电流和转速作为输入和输出数据,利用遗传算法对异步电机的离线参数辨识进行了研究,但此参数辨识后期个体太过单一。
Stribeck摩擦模型作为参数辨识的基本模型,可较好地描述零速附近的摩擦力动态特性,解决零速附近的非线性问题。相比经典遗传算法,改进后的遗传算法采用自适应算子策略,即随着代数的增加,算子也随之改变,有利于维持种群的多样性,有效防止局部最优解的出现。
1.1 Stribeck摩擦模型
Sribeck摩擦模型具有很多区别于其他模型的优势:参数较少、便于辨识、对零速附近的摩擦特性具有很好的描述,可在其基础上进行修改完善,建立更符合管道机器人工作特性的摩擦力模型。Stribeck摩擦模型的数学描述为
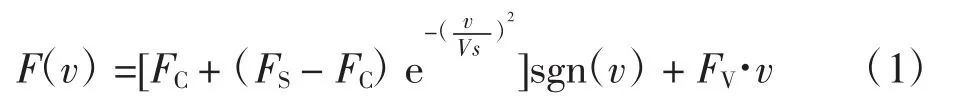
其中:F(v)为摩擦力;FC为库伦摩擦力;FS为最大静摩擦力,即Stribeck曲线与摩擦力轴相交时的纵坐标值,FV为粘性摩擦系数;VS为速度。当速度v方向相反时,对应的Stribeck摩擦模型各参数也存在差异,并在后续的改进遗传算法验证过程中分别进行参数辨识。
1.2 改进遗传算法设计
在摩擦参数辨识中,参数辨识算法的原理如下。
1)用激光位移传感器测出管道机器人电机失能直至停止的过程中电机的速度及其加速度,测得管道机器人所受的摩擦力及其速度。
2)对Stribeck摩擦模型中待辨识的参数划定范围,用改进遗传算法进行辨识,其目标函数为

其中:M为所测数据的数目;F测为实验测量所得摩擦力;F拟为通过改进遗传算法辨识后得到的摩擦力。
3)遗传算法的适应度函数为

其中,a为目标函数中的一个常数参数。
4)将待辨识的参数设为遗传算法的个体进行编码(编码长度由目标精度决定),经过N代进化,求出最优解对应的参数。
5)确定代沟值。代沟值的大小决定了每进化一代,子代群体个数占父代群体的比例,能够很大程度上加快子代群体的更新。
6)确定交叉算子。交叉算子的大小影响子代群体的多样性,尤其是在进化过程的渐进阶段(即前期),因此,算法采取自适应交叉算子方式,即进化前期阶段,交叉算子值较大,随代数增加交叉算子逐步减小的策略[4]。交叉算子变化曲线如图2(a)所示。交叉算子为

其中:gen 为子代对应的遗传代数;k1、k2、PCa、PCb为交叉算子公式中的常数参数。
7)确定变异算子。变异算子的大小直接影响进化后期子代群体的多样性,避免进化后期(突变阶段)群体太过单一[5]。因此,采取动态改变变异算子的策略,使得变异算子随着代数的增加呈上升趋势。变异算子变化曲线由图2(b)所示。变异算子为
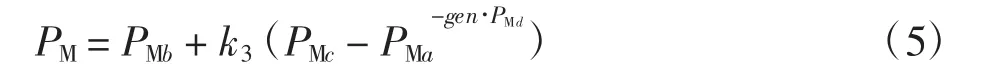
其中:gen 为子代对应的遗传代数;k3、PMa、PMb、PMc、PMd为交叉算子公式中的常数参数。

图2 交叉算子和变异算子变化曲线Fig.2 Variation curve of cross-over operator and mutation operator
8)将步骤1)~步骤3)过程循环指定的次数,对每次求得的最优值参数做算术平均运算,求得最优参数。
2 结果分析
利用仿真和实验验证算法的有效性。对Stribeck摩擦模型在相反速度方向分别进行了摩擦参数辨识,辨识精度较高,接近理想值。在管道机器人本体基础上搭建实验平台,通过实测数据,对改进算法作进一步验证和应用。
2.1 Stribeck摩擦模型参数辨识与动力学仿真
为检验上述算法的参数辨识精度,以Stribeck摩擦模型曲线拟合为例,用Matlab语言编写程序,进行参数辨识,并观察辨识前后曲线的拟合情况。
由于Stribeck摩擦模型在改变速度方向时,对应的摩擦模型参数也会发生改变,因此Stribeck摩擦模型可进一步表示为


图3 实际值和辨识值的Stribeck曲线比较Fig.3 Stribeck comparison curve between actual and identified values
理论值及辨识结果如表1所示,参数辨识误差小于5%,改进遗传算法辨识参数效果符合预期,可进一步验证和应用。

表1 Stribeck摩擦模型实际值、辨识值及误差Tab.1 Actual value,identified value and errors of Stribeck friction model
实验前首先利用Adams对管道机器人进行动力学分析,进一步了解机器人运动过程中在各个方向上的震动情况,各方向的动力学方程[7]如式(8)所示,动力学模型如图4所示。

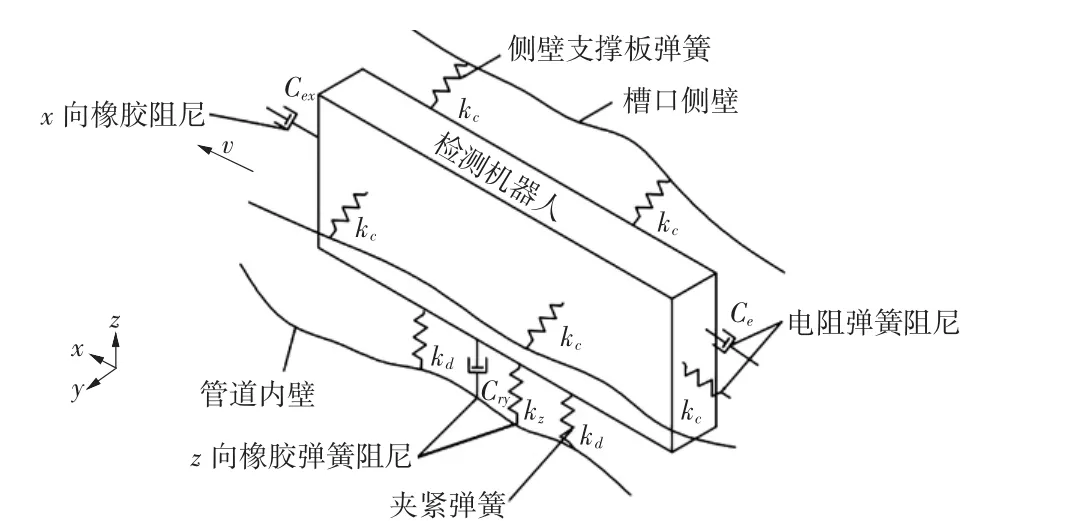
图4 机器人动力学模型Fig.4 Dynamic model of robot
机器人运动过程中在x和y方向上随时间变化的位移曲线如图5(a)、图5(b)所示。由动力学分析可得出,在各个方向上都会有一定程度的振动和角度偏转,这对于精度要求较高的参数辨识,尤其是z方向振动位移的变化而言是不能忽略的[8]。
2.2 实验设计与结果分析
为将改进遗传算法应用到生产实践中,使其辨识结果成为摩擦力计算的重要参考,设计了测量实验。管道机器人在减速过程中,通过LSR系列激光位移传感器以及自带的操作界面测量得出加速度随时间的变化曲线。根据LSR系列激光位移传感器的测量原理,传感器发射的激光应与所投射的运动体金属表面尽可能保持垂直状态,测量结果才会准确[9]。
由动力学仿真结果可得,管道机器人在运动过程中各方向上都有一定程度的震动,真实实验环境更为复杂,也正因为实验环境比较嘈杂以及减速过程中管道机器人本体的震动,使得实验数据存在明显的杂波,需进行滤波预处理[10]。图6~图7分别为实验所测数据、经过滤波后的加速度曲线图。自适应遗传算法辨识前后的曲线对比如图8所示。基于实验所测数据以及摩擦特性分析,在基本摩擦模型中引入正弦选项,修正后的摩擦模型[11]为

图5 机器人沿z、y方向振动位移Fig.5 Robot vibration along z and y directions

图6 实验测得的加速度Fig.6 Measured acceleration data
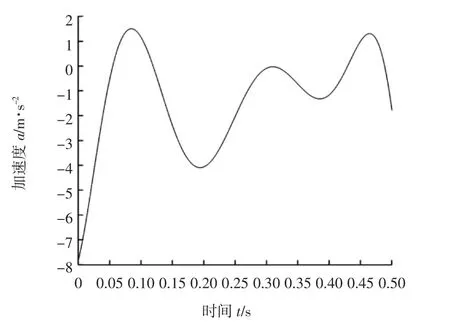
图7 经滤波后的加速度曲线Fig.7 Filtered acceleration curve after filtering
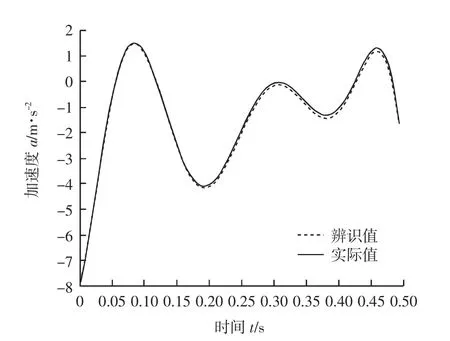
图8 遗传算法辨识前后的曲线对比Fig.8 Curves comparison before and after genetic algorithm identification
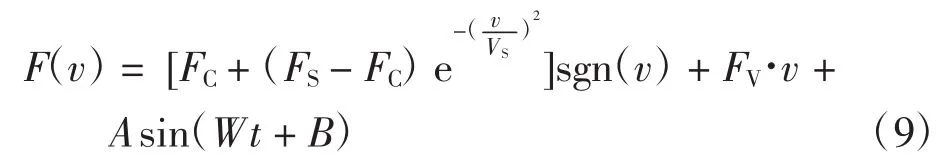
实验过程考虑速度大于0的情况,则摩擦模型为

辨识结果如表2所示。

表2 修正后的摩擦模型参数及辨识值Tab.2 Parameters and identified values of modified friction model
在管道机器人的运动过程中,摩擦热会使接触面温度升高,运动速度和温度会对粘着磨损造成很大的不利影响。通过实验测出运动速度和摩擦力,应用改进遗传算法进行摩擦参数辨识,辨识精度越高,所获取的摩擦力值越接近实际值。由表1、表2和图8可知,算法得出的参数辨识精度很高,可较好地跟踪实际所测得的摩擦力曲线,帮助研究人员实时获取管道机器人在运动过程中所受的摩擦力,对于研究管道机器人磨损状态提供了实验数据,为动力学及其他摩擦研究提供参考。
3 结语
提出一种改进的自适应遗传算法,基于经典的Stribeck摩擦模型,对模型的4个参数进行辨识,误差控制在5%以内,有效避免了局部最优解的问题,验证了算法的可行性;然后搭建实验平台,将实验数据进行滤波预处理后,绘制加速度及速度曲线,有效消除了碰撞对摩擦的影响,运用改进后的自适应遗传算法跟踪摩擦力曲线,误差较小,满足精度要求。但仍需指出,受实验条件限制,仅对管道机器人减速过程中的运动特性进行了实验研究,对于整个运动过程中的运动特性以及摩擦研究,还需进一步实验论证。

