一种消除BOC(m,n)信号自相关函数副峰的方法
王 剑,戚涵天
(中国民航大学a.民航空管研究院;b.中欧航空工程师学院,天津 300300)
与二相相移键控(BPSK-like,binary phase shift keying-like)相比,BOC信号的相关性更好[1],且可将信号的频谱分离。BOC调制中自相关函数(ACF,autocorrelation function)的主峰相对于相同码速率的BPSK调制更为狭窄陡峭,利用这一特点可提高码跟踪精度。频谱分离可以解决频带拥挤的问题,避开已经占用的频段。但在捕获和跟踪过程中,BOC信号自相关函数的多峰现象会引起捕获模糊。相邻副峰的幅度与主峰接近,使用传统的算法容易将信号锁定到副峰上,从而产生错误的捕获。
为解决此关键问题,研究人员提出了不同的捕获方法。BOC信号的直接处理法[2]与传统的处理方法相似,如时域串行搜索、频域FFT捕获等,有学者结合时域和频域的时频并行捕获算法[3]有效提高了捕获效率。这些方法将接收信号与本地产生的BOC信号进行相关以判定是否捕获成功,实现起来比较简单,但捕获效果非常不理想。BPSK-like方法[4]属于单边带处理算法,处理新型BOC信号的方法与BPSK信号的处理算法类似。由于BPSK信号的功率谱经过平移后和BOC信号的功率谱主瓣形状接近,对BOC信号进行滤波、相干合并等处理,得到类似于BPSK信号形式的相关结果,将多峰自相关函数转化成类似BPSK信号的单峰三角形函数,可解决BOC调制方式中出现的多峰模糊问题。BtoB算法通过将左右边带频谱进行相位翻转处理后再叠加的方式,对捕获性能和计算量进行了折中[5]。BPSK-like算法能够处理一般的BOC信号,没有充分利用BOC调制的高精度特点,在处理过程中伴随着较大的能量损失。相关函数法是利用相关函数的几何特性来消除BOC的调制模糊度。对于此类问题的相关研究多集中在 BOC(n,n)类信号,主要有 ASPeCT[6]、ACF+AACF[7]、Filter[8]等算法。一些新型的捕获算法降低了运算量[9];有些算法对Filter算法进行了改进,保留原算法提高主峰峰值优点的同时进一步消除了副峰,提高了捕获性能[10]。文献[11]提出了基于FPGA的BOC信号捕获算法;新型精确同步方法可在消除副峰的同时保持优良的抗多径性能,但检测概率只是略有下降[12]。上述方法都只适用于BOC(n,n)族系列信号捕获,但不适用于其他族类信号。ASPeCT算法在相关函数领域上提供了创造性的思路,被广泛应用于信号接收机捕获模块的设计[13],且在其基础上,提出了适用于BOC(2n,n)信号的捕获方法,解决了更多类型信号的捕获模糊问题[14-16]。但这些算法也只能处理特定类型的BOC信号,而能够处理通用信号的算法[17]也往往需要对副载波进行大量的分解重构,硬件的实现比较复杂。
北斗系统采用的调制方式有QPSK、BOC、MBOC和ALTBOC,超过一半的信号使用新型或其衍生的调制方式。利用BOC(m,n)信号的自相关函数副峰的特点,提出了降低或消除副峰的方法,其适用于任意的BOC(m,n)信号。仿真表明,该算法可有效减弱自相关函数的副峰,能提高主峰与副峰的比值。
1 BOC信号特性
1.1 BOC(m,n)的自相关函数
经过BOC调制的信号,其频谱会产生分裂,能量峰在功率谱密度曲线上向左右两边平移一定间隔。副载波频率fs和码率fc是描述BOC调制的两个重要参数,表示为 BOC(fs,fc)。在实际使用过程中,fs和 fc通常都是基准频率f0=1.023 MHz的整数倍,因此常用BOC(m,n)来表示BOC调制。其中m表示副载波频率相对于基准频率的倍数(fs=m f0),n表示码率相对于基准频率的倍数(fc=nf0),调制阶数N=2m/n。
BOC信号的频谱和自相关特性决定了BOC信号的频率搬移量和自相关函数的副相关峰个数,改变这两个参数的设置,能够选择性地避开已被占用的频段,实现频带共享。
若二进制序列为[c1,c2,…,cn],则 BOC 信号序列可表示为
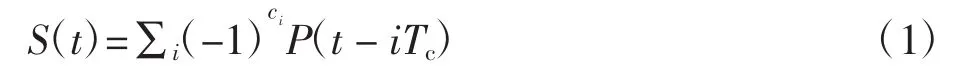
其中:ci∈{0,1};Tc为码元宽度;P(t)为副载波调制的码信号。BOC(m,n)的自相关函数[16]为

式中,k=0,1,…,N-1,N越大,RBOC(τ)的形式越复杂。
图1 和图 2 分别是 BOC(2,1)和 BOC(4,1)的自相关函数。随着调制阶数的增大,BOC信号的副峰数量也相应增加。

图1 BOC(2,1)自相关函数Fig.1 ACF of BOC(2,1)signal
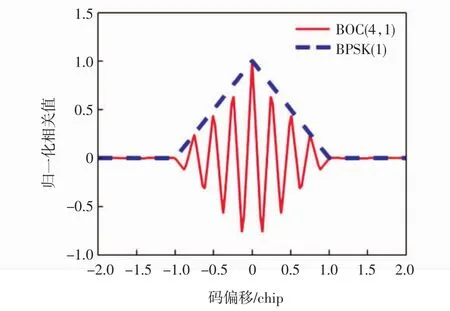
图2 BOC(4,1)自相关函数Fig.2 ACF of BOC(4,1)signal
1.2 副峰补偿相关函数的数学模型

算法的目的是消除副峰的同时尽量保持主峰,即当k取非0值时,R(k)的结果为0,而k=0时,主峰幅度R(0)不为0。为了达到这一目的,该算法使用第k个副峰的前一副峰和后一副峰的算术平均值来补偿第k个副峰的幅度R(k)(k≥1),称为补偿相关函数(SCF,supplementcorrelation function)。
第k个副峰的叠加结果为
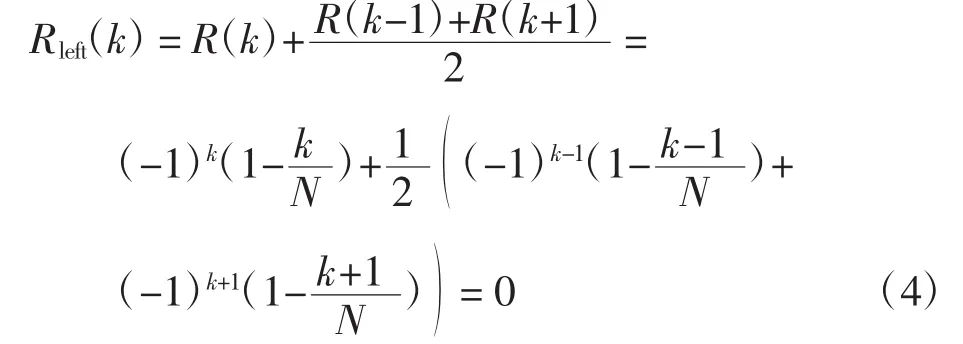
而对于主峰幅度R(0),由于自相关函数的对称性,R(-1)=R(1),主峰剩余幅度为
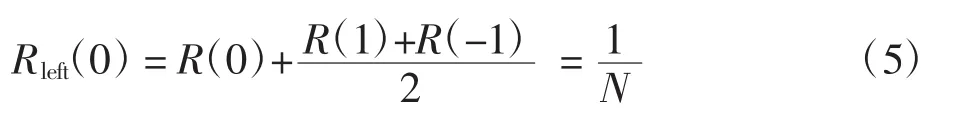
此时相关函数的副峰得到了消除,而主峰幅度依然有所保留,其幅值大小为调制阶数N的倒数。
由图1、图2可知,BOC信号的自相关函数关于中心轴对称,且幅度集中在[-Tc,Tc]之间,各峰平均宽度M=2Tc/(2N-1),呈平均分布。因此,只需分别将原始BOC自相关函数进行左右平移2Tc/(2N-1)的宽度,并与原BOC自相关函数叠加即可实现上述副峰幅度的补偿。
该算法处理后得到函数的最终形式为
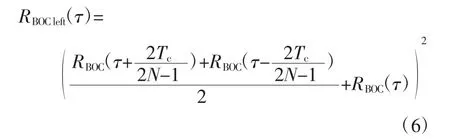
其中:RBOC为本地BOC信号的自相关函数;Tc为码元宽度。
1.3 算法流程和结果
单峰相关函数算法原理的流程图如图3所示。
首先调整信号调制参数(m、n)的取值,与需要捕获的信号相匹配;当接收机接收到BOC信号后,生成本地BOC信号,获得原始的BOC自相关函数;分别将BOC自相关函数向左、右平移M长度;将平移后的两个函数相加取平均,再与原自相关函数叠加,取模平方并进行归一化放大,所得结果如图4所示。
由图4可知,该算法对BOC(1,1)信号副峰的处理效果良好,信号的两个副相关峰的幅值被大幅降低,而中心主峰的宽度得以保留。为验证该算法对任意m、n都适用,分别对北斗系统所使用的BOC(15,10)、BOC(14,2)、BOC(15,3)信号运用该算法,结果如图 5所示。
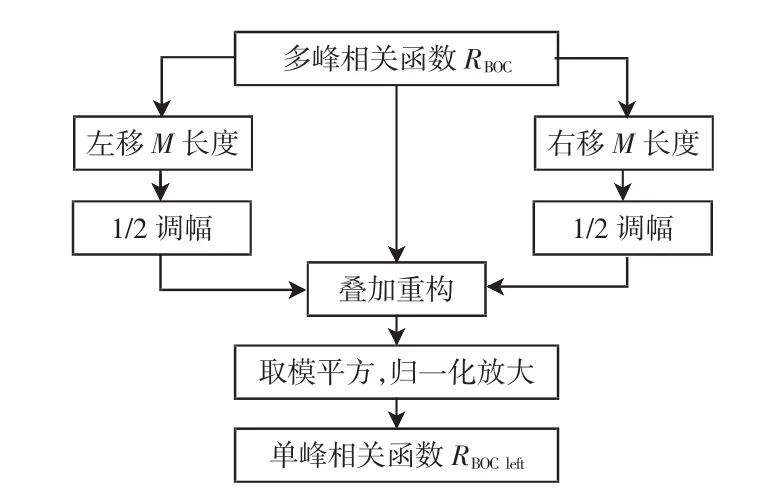
图3 算法原理图流程图Fig.3 Flow chart of proposed algorithm
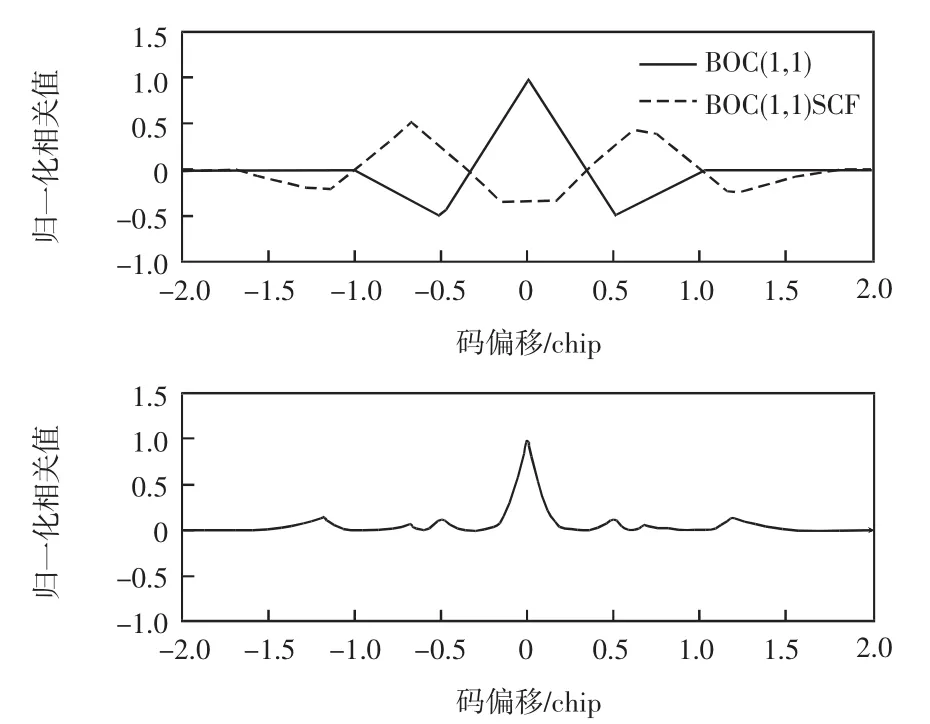
图4 算法运用前后BOC(1,1)相关函数Fig.4 CFs of BOC(1,1)signal before/after algorithm processing
由图5可知,该算法有效地抑制了BOC信号相关函数的副峰,保留了BOC信号的窄带主峰,主峰宽度≤2Tc/(2N-1)。
常见的相关函数算法,如ASPeCT算法等,只适用于BOC(n,n)族信号,不能处理其他信号的多峰问题;BPSK-like算法虽然能够处理一般的BOC信号多峰问题,但其主峰宽度增加到BPSK信号宽度2Tc,精度严重降低。该算法在消除信号族类限制的同时,保留了BOC调制信号高精度的优点。
2 捕获过程仿真和性能分析
2.1 捕获过程
采用BOC(14,2)信号对该算法捕获进行试验。设定伪码长度为1 023,则BOC信号码长度为14×1 023=14 322。设置载波频率为9.548 MHz,采样频率为2×38.192=76.384 MHz。加入43 dBHz(载噪比)的噪声和随机的多普勒频移,搜索范围为9 548±7 kHz,步长500 Hz,捕获阈值(主峰/第一副峰)2.5,结果如图6所示。此次仿真的多普勒频率为-4.538 7 kHz,码相位偏移为850×14=11 900。
图6仿真结果是该算法的一次成功捕获,其参数与仿真的预设一致,说明了该算法的可行性。
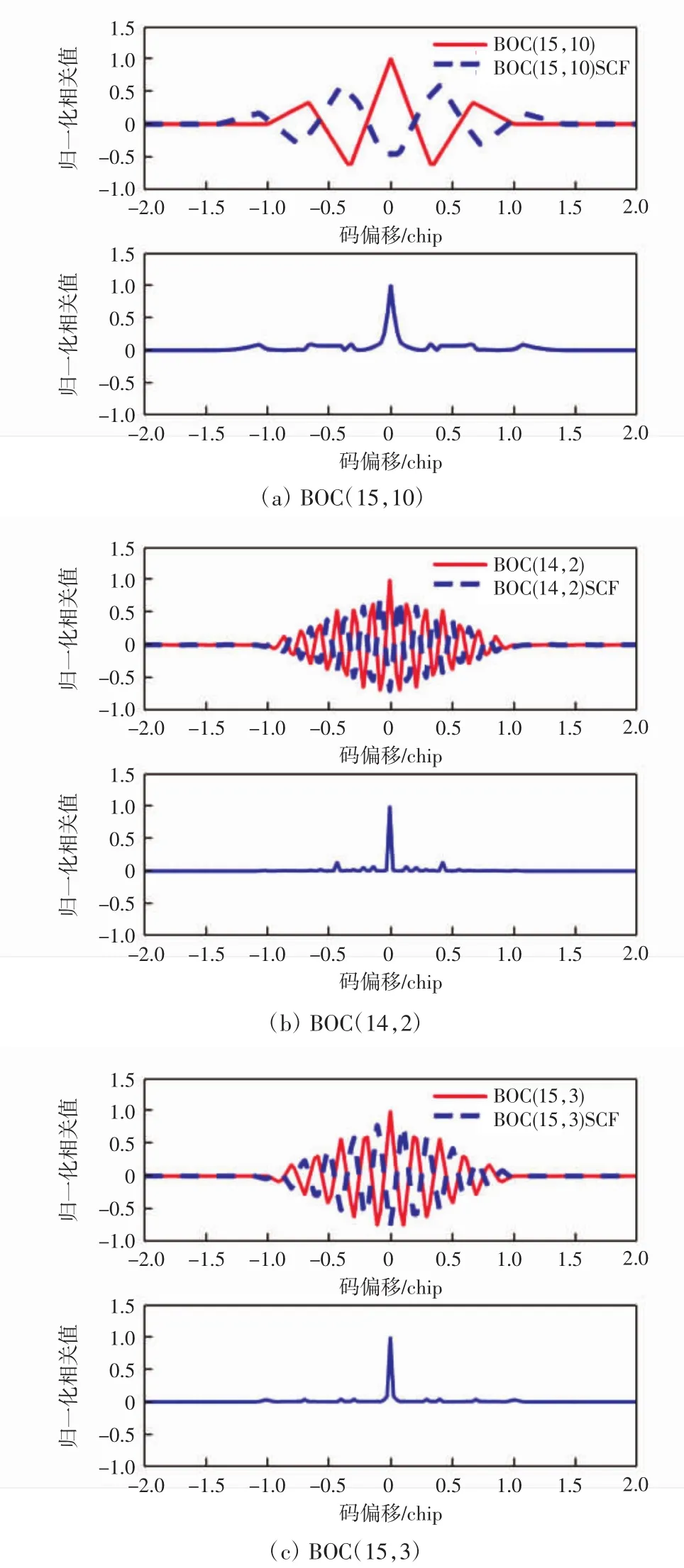
图5 算法运用前后相关函数对比Fig.5 CFs before/after algorithm processing
2.2 捕获率
信号捕获率是评价捕获算法的重要指标,在解决信号多峰问题的同时,还需考虑实际BOC信号在传输处理过程的噪声干扰。为了定量研究噪声对该算法捕获率的影响,将该算法的抗噪性能与BPSK-like算法进行了比较。同样使用BOC(14,2)信号,结果如图7所示。
从仿真结果可以看出,该算法的性能明显优于BPSK-like算法。
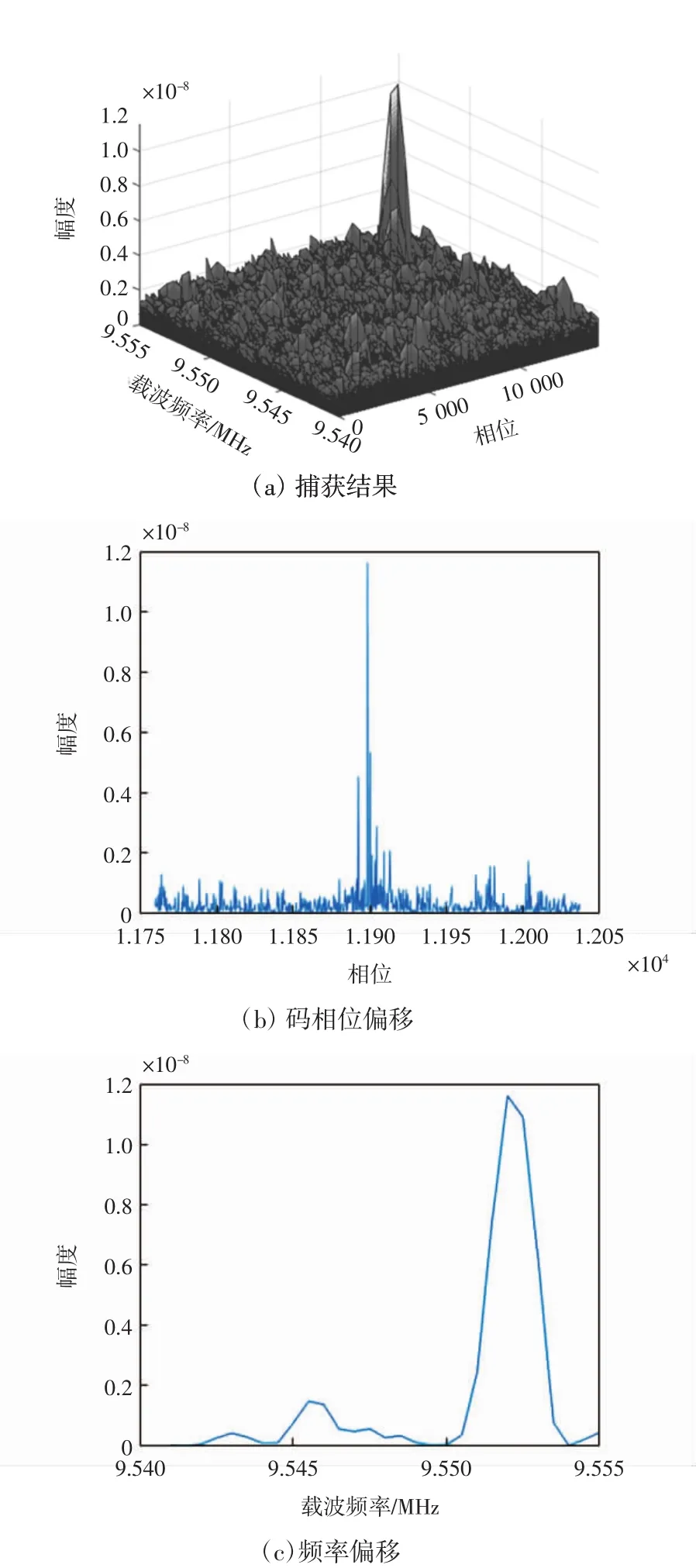
图6 捕获结果Fig.6 Acquisition results
3 结语
针对BOC信号的多峰捕获问题,研究了BOC信号自相关函数各峰之间的关系,提出了一种通过构造合成相关函数消除信号自相关副峰的算法,给出了算法的流程和步骤。结果表明,该算法能够抑制BOC信号的副峰,保持BOC信号主峰宽度的同时提高了主副峰的峰值比,避免了BOC族类信号中m、n取值的限制,仿真结果验证了其捕获的有效性。该算法的缺点在于相关函数的运算当中含有噪声,对信号的载噪比需求较高,但仿真实验表明,该算法的抗噪性能依然优于传统的BPSK_like算法。

图7 捕获率Fi.7 Acquisition rate

