一类食饵具有脉冲生育和Iv1ev型功能性反应的食饵-捕食者模型的动力学分析
梁桂珍,刘蒙蒙,2
(1.新乡学院 数学与信息科学学院,河南 新乡 453003;2.郑州大学 数学与统计学院,河南 郑州 453000)
以常微分方程为基础发展起来的脉冲微分方程能反映物种瞬间的变化,能更加合理、形象地描述现实生活中很多生命现象和人类对生物种群的放养、收获等行为。近年来,人们越来越多地将脉冲控制方法应用于种群系统持久性和稳定性方面的研究[1-4]。 陈兰荪等[5]研究了不同脉冲时刻的收获捕食者和生育食饵,但没有考虑功能性反应函数。人们在研究生物种群时常用Machaelis-Menten 型、Beddington-Deangelis型、Holling I型、Holling II型、Holling III型和Holling IV型功能性反应函数,而很少用到Ivlev型功能性反应函数。焦建军等[6]研究了捕食者是脉冲投放捕食者,且具有脉冲扰动和Ivlev型功能性反应函数的捕食-食饵模型。陈兰荪[7]研究了具有生育脉冲效应的单种群模型。在本文中,我们在模型[8-9]的基础上研究了一类带有Ivlev型功能性反应函数的食饵具有生育脉冲效应和捕食者具有连续收获的食饵-捕食者模型,建立了如下的捕食系统:
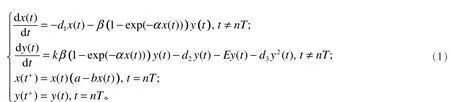
1 基本引理
引理 1[10]:设是系统(1)的解,且有则对所有的 t ≥0,均有 z (t)≥0。 若 z (0+)≥0,则当时,均有 z (t)≥0。
引理 2[11]:假设函数满足不等式组
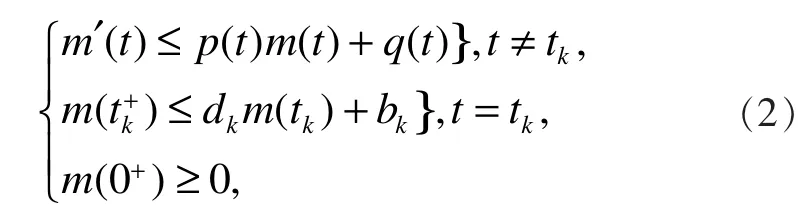
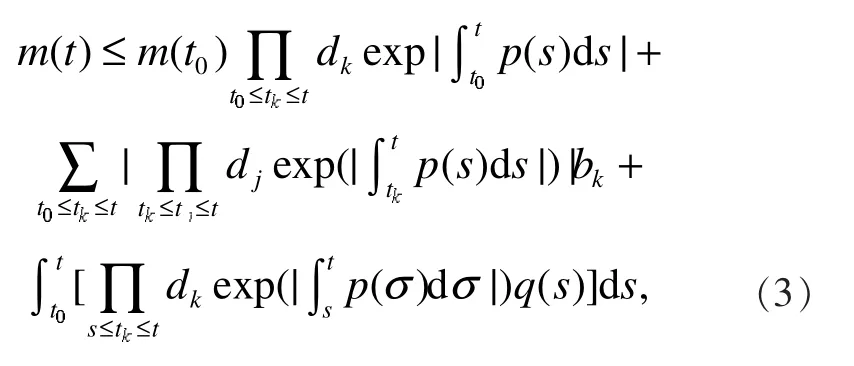
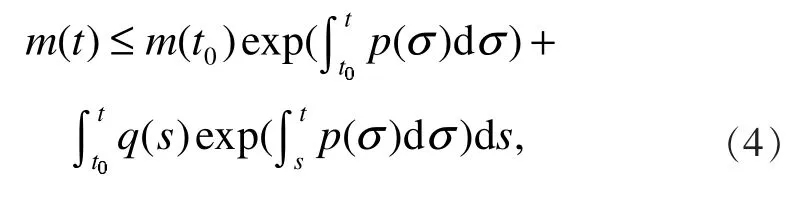
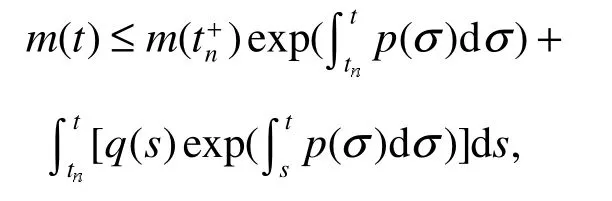
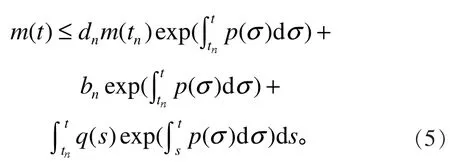
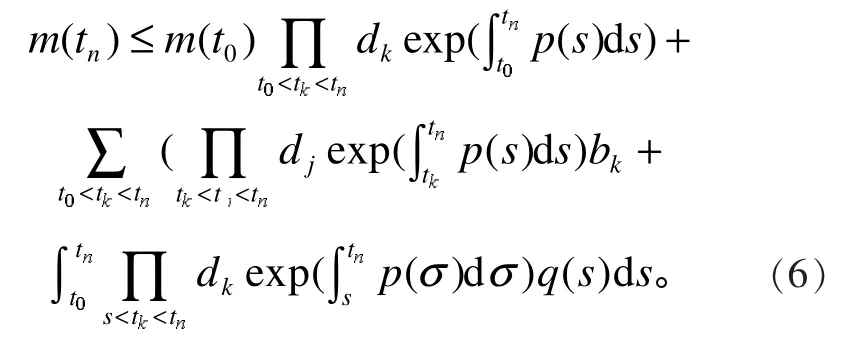
把式(6)代入式(5)可得
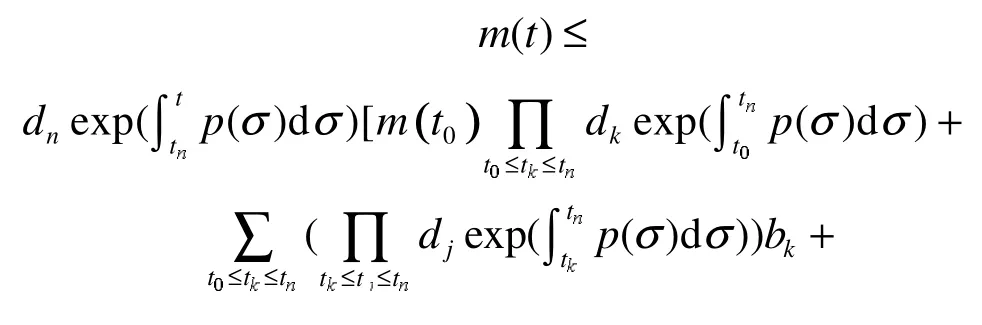
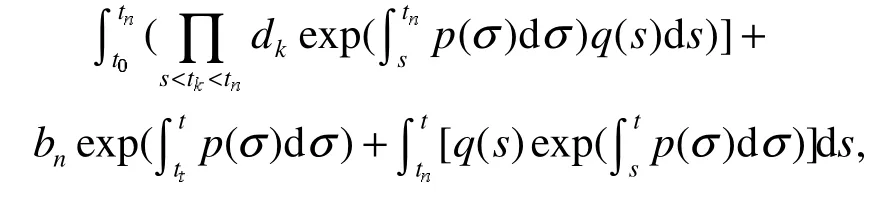
经过合并和化简可得式(3)。

由引理2可知

引理 4[12]:脉冲系统
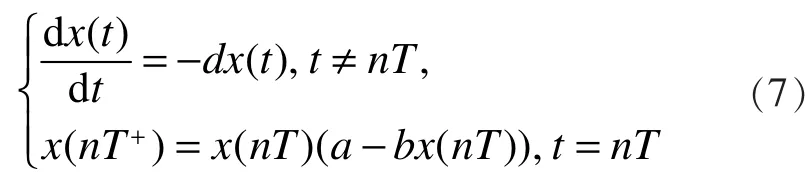
有一个全局渐近稳定的周期解

2 系统的持久性

考虑如下脉冲微分方程
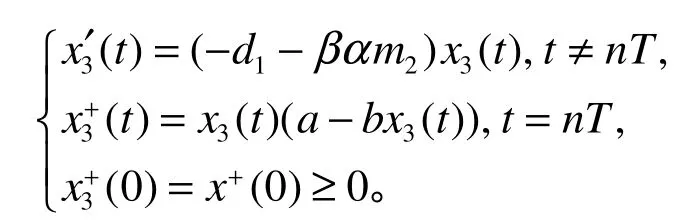
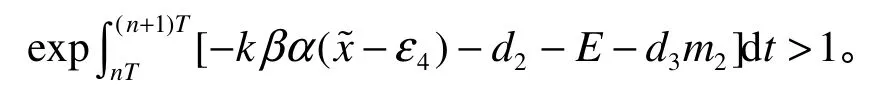
由系统(1)的第2个方程和第4个方程可得:
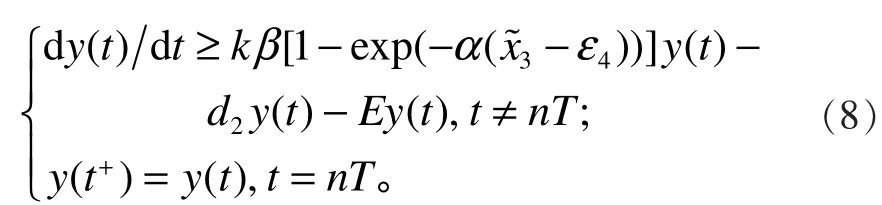
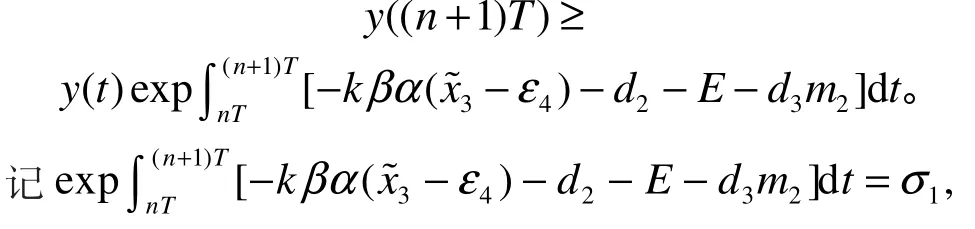
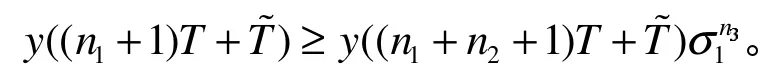
由系统(1)可得:
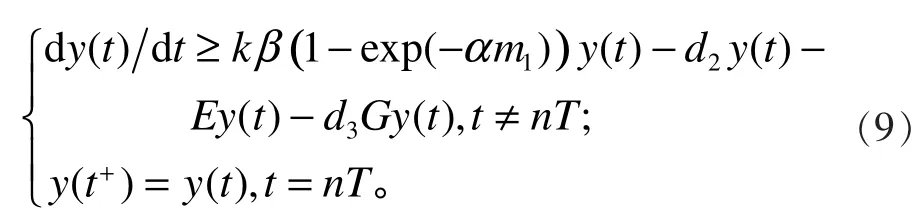
3 捕食者灭绝的全局渐近稳定性
由引理4可知,当捕食者灭绝时,系统(1)可简化为系统(7)的形式,故存在相应的周期解为当时,有
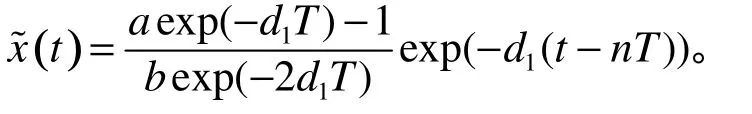
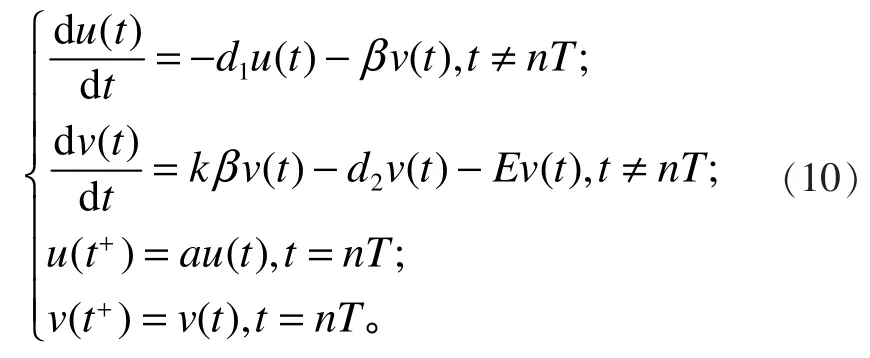
因此,捕食者灭绝的周期解稳定性问题就转化为系统(10)零解的稳定性问题。
系统(10)的变分方程的任意解为

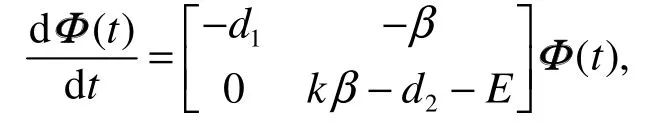
且有

由脉冲微分方程的Floquet乘子理论可知,如果单值矩阵的特征值小于1,周期解就是局部渐近稳定的。
A的两个特征值分别为

下面证全局吸引性。由系统(1)的第1和第3个方程,有:
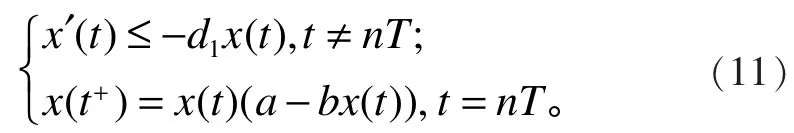
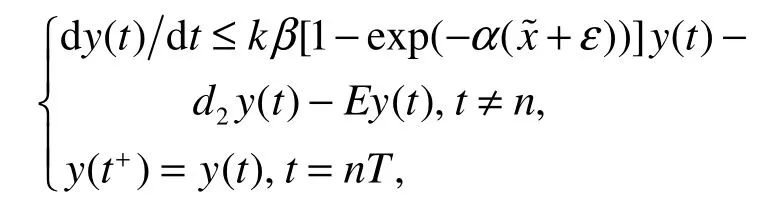
即

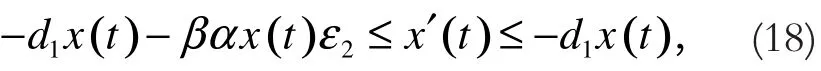
x1(t)且其中,和是下列两个脉冲微分方程的解。
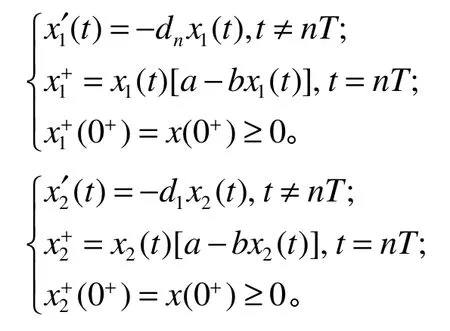
由引理4和脉冲微分方程比较定理,可得:对于充分大的t和任意给定的总有
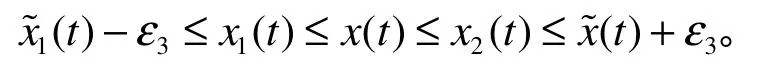
4 数值模拟
为了验证定理1的正确性,即系统(1)的全局渐近稳定性,建立如下系统:
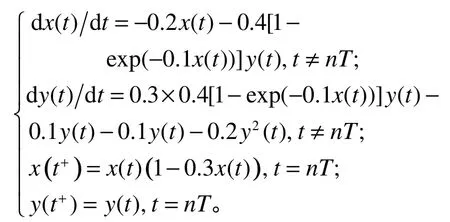
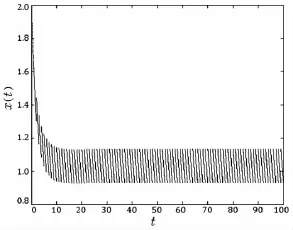
图1 食饵持续生存的种群时间序列
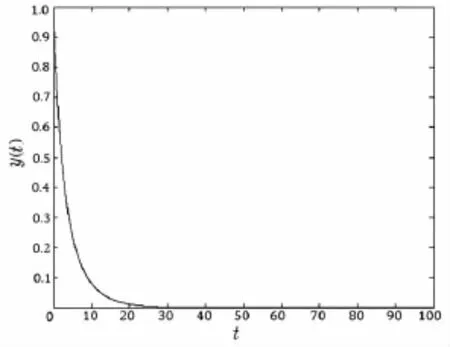
图2 捕食者灭绝的种群时间序列

