壳聚糖涂膜鸡蛋贮藏中品质变化的动力学模型
胡云峰,张利苹,位锦锦,魏增宇,陈君然
(天津科技大学重点实验室,天津300457)
鸡蛋是重要的动物蛋白质来源,含有大量的脂肪、矿物质、维生素、卵磷脂等多种营养物质,深受广大消费者喜爱[1]。鸡蛋属于活体物质,因其本身特性,在贮藏及流通过程中易受微生物污染导致腐败变质[2-3],还会发生复杂的物理化学和生理变化,从而影响其食用品质和作为功能性配料在食品加工中应用[4]。鸡蛋涂膜可以达到保鲜的效果,以延长其货架期。壳聚糖是目前研究最多的多糖类天然高分子,因具有良好的成膜性、气体阻隔性和特有的抗菌性,且壳聚糖膜可以对鸡蛋起到“微气调”的作用,因此在鸡蛋的涂膜保鲜中已有广泛研究[5-6]。
近年来,国内学者利用动力学模型对肉制品、蔬菜、水果等的品质变化进行研究,并预测其贮藏期,得到较好的效果。柴春祥[7]研究了猪肉品质变化的动力学模型;谢晶等[8]研究了上海青蔬菜的品质变化动力学模型及货架期预测;张倩钰等[9]研究了苹果片热风薄层干燥过程中颜色变化的动力学模型。关于鸡蛋在贮藏过程的动力学模型研究较少,仅有基于回归方程拟合的模型[10]。因此本文以壳聚糖涂膜鸡蛋为原料,研究不同贮藏温度下的各指标的变化规律,为壳聚糖涂膜鸡蛋的贮藏和销售提供参考。
1 材料与方法
1.1 材料与仪器
新鲜鸡蛋 天津市团泊湖养鸡场;壳聚糖 河南金诚生物科技有限公司;甘油 分析纯,天津市大茂化学试剂厂;冰乙酸 分析纯,天津市风船化学试剂科技有限公司。
PL203/01电子分析天平 特勒-托利多仪器(上海)有限公司;游标卡尺 天津精密仪器厂;78-1型磁力搅拌器 金坛市江南仪器厂;照蛋灯、MP522型p H计 上海理达仪器厂;MHP-250型智能霉菌培养箱 上海鸿都电子科技有限公司;DL-1型万能电炉 北京中兴伟业仪器有限公司。
1.2 实验方法
1.2.1 鸡蛋前处理 向98 mL蒸馏水中加入2 g壳聚糖[11],用冰乙酸调溶液 p H 为5.0~5.6,磁力搅拌直至完全溶解,加入2%的甘油,搅拌均匀。将鸡蛋浸入搅拌均匀的溶液中5 s,拿出烘干后备用。然后把涂膜后的鸡蛋分别贮藏在5、10、15、20、35℃的环境中,处理当天记为第 0 d,在第 0、5、10、15、20、25、30、35、40、45、50 d分别对鸡蛋进行指标的测定。1.2.2 指标测定
1.2.2.1 鸡蛋贮藏期间的重量变化 各取10枚鸡蛋,分别用精度为0.001 g电子天平称重。
1.2.2.2 鸡蛋贮藏期间气室直径变化 用照蛋灯从鸡蛋小的一端打光,用游标卡尺分别测量不同贮藏条件的鸡蛋气室最大部分的直径,每次测量10枚鸡蛋,取平均值[12]。
1.2.2.3 鸡蛋贮藏期间蛋黄系数的变化 将蛋内容物全部倒入水平放置的玻璃板上,用精度为0.2 mm的游标卡尺测量蛋黄竖直方向最大厚度,即为蛋黄高度;同时测定蛋黄直径(以蛋黄与蛋清间的黄白交界为线),取10 枚鸡蛋的平均值[13]。
蛋黄系数=蛋黄高度(cm)/蛋黄直径(cm)
1.2.2.4 鸡蛋贮藏期间哈夫单位的变化 根据鸡蛋质量与蛋白高度的回归关系得出,先用0.2 mm的游标卡尺测量鸡蛋的浓蛋白高度,再根据式(1)计算得出哈夫单位值[13]:
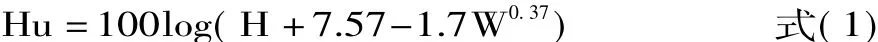
其中,Hu:鸡蛋的哈夫单位值;H:浓蛋白高度(mm);W:鸡蛋质量(g)。
1.3 模型的建立与验证
1.3.1 确定品质变化反应速率常数k的确定 利用数学统计软件对试验中鸡蛋各项品质指标变化数据进行线性和非线性拟合,得到拟合曲线,对应求出各项指标变化的零级和一级反应速率常数k。零级反应速率常数为线性拟合的斜率,一级反应速率常数为品质指标值的对数与时间曲线的斜率[14-15]。根据判定系数R2的大小,选用各指标拟合度比较高的动力学模型。
1.3.2 反应活化能的确定 模型方程中的参数包括A和Ea,确定两个参数常用的方法是作图法。将Arrhenius方程两边分别取对数,化成对数形式,如式(2)所示[16-17]。以 lnk 为纵坐标,1/T 为横坐标,作出lnk与1/T之间的关系曲线依据可得到的直线,由直线的截距和斜率可分别确定A和Ea,直线的斜率为直线的截距值为lnA的值。

1.3.3 模型方程的建立 根据式(1)中的拟合结果,分别选择不同的模型方程。零级和一级反应模型方程如式(3)和(4)所示:
零级反应模型方程:

一级反应模型方程:

结合Arrhenius方程,推导得出品质指标预测模型。品质指标零级和一级动力学变化预测如式(5)和(6)所示:
零级动力学预测模型:

一级动力学预测模型:
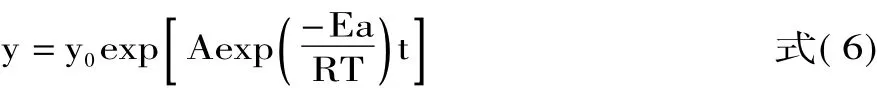
1.3.4 品质模型的验证 通过计算对比平均相对百分比误差来确定验证模型[18-19],其计算公式为:
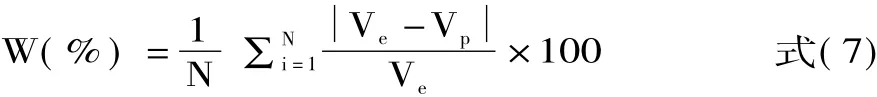
式(7)中:Ve、Vp分别为每次试验的实测值和预测值;N为试验次数,w均值小于10%时,认为建立的品质模型符合动力学变化。
1.4 数据处理
用Excel进行数据整理及相关数据的拟合与计算,应用SPSS统计软件进行相关性分析,验证模型的合理性。
2 结果与分析
2.1 鸡蛋各指标数据拟合分析
根据实验结果所呈现的色泽指标变化规律,对所得数据进行线性和非线性拟合,分别可得到零级和一级动力学回归速率常数k和决定系数R2。由表1中∑R2的结果可知,气室直径的零级动力学模型的决定系数之和为4.7968,大于一级动力学模型的决定系数4.6694,而重量、蛋黄系数和哈夫单位的一级动力学模型的决定系数之和分别为4.8771、4.7327、4.9125,大于零级 4.8612、4.6116、4.8591。因此,气室直径选用零级动力学模型,重量、蛋黄系数和哈夫单位选用一级动力学模型。

表1 零级和一级动力学回归速率常数k及决定系数R2Table 1 Rection rate constant k and determination coefficient R2 of determination for zero and first order regression
2.2 气室直径变化的预测模型建立与验证
2.2.1 气室直径变化的预测模型建立 根据不同贮藏温度下鸡蛋气室直径随时间变化的规律,可以建立气室直径随着贮藏时间变化的零级动力学模型。用气室直径的回归方程的速率常数对数值(lnk)与对应的温度倒数(1/T)所做的Arrhenius曲线如图1所示,其决定系数为0.9611,这表明本试验选用的零级动力模型跟 Arrhenius方程结合效果较好。由Arrhenius方程计算得到贮藏期间鸡蛋气室直径Ea为4.50×104kJ/mol,A 值为2.42×106。

图1 鸡蛋气室直径的Arrhenius曲线Fig.1 Arrhenius curves of air chamber diameter of egg
根据不同贮藏温度下实验数据统计能够得出气室直径的动力学方程,并能结合Arrhenius方程计算出反应速率常数k、A和Ea,可建立鸡蛋气室直径的最终预测模型方程。最终动力学模型方程如式(8)所示:
气室直径预测模型方程:
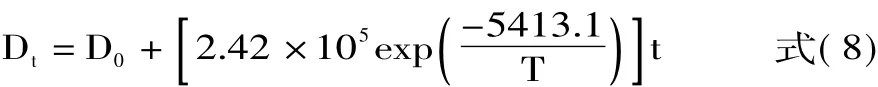
式中,Dt表示贮藏 t时间后,气室直径大小(cm);D0表示起始时刻气室直径大小(cm)。
2.2.2 气室直径变化的预测模型的验证 用鸡蛋气室直径预测模型方程计算出验证组中25℃条件下鸡蛋的气室直径,即为鸡蛋气室直径的预测值,将其和实测值进行比较(图2)。结果表明,由公式计算得到的鸡蛋气室直径预测值和实测值基于1∶1曲线的决定系数为0.9797,根据式(7)计算得出的平均相对误差w为1.95%,小于10%,说明模型能较好的预测5~35℃条件下鸡蛋的气室直径。

图2 气室直径模型实测值与预测值之间的相关性Fig.2 Correlation between predicted values and actual values of prediction models
2.3 鸡蛋重量、蛋黄系数变化的预测模型建立与验证
2.3.1 鸡蛋重量、蛋黄系数的预测模型的建立 根据不同贮藏温度下鸡蛋重量、蛋黄系数随时间变化的规律,可以建立鸡蛋重量、蛋黄系数随着贮藏时间变化的一级动力学模型。用鸡蛋重量、蛋黄系数的回归方程的速率常数对数值(lnk)与对应的温度倒数(1/T)所做的Arrhenius曲线如图3(a)、(b)所示,决定系数分别为0.9876、0.9846,这表明本试验选用的一级动力模型跟Arrhenius方程结合效果较好。由Arrhenius方程计算得到贮藏期间鸡蛋重量、蛋黄系数 Ea分别为2.83×104、5.38×104k J/mol,A 分别为195.76、7.11 ×107。
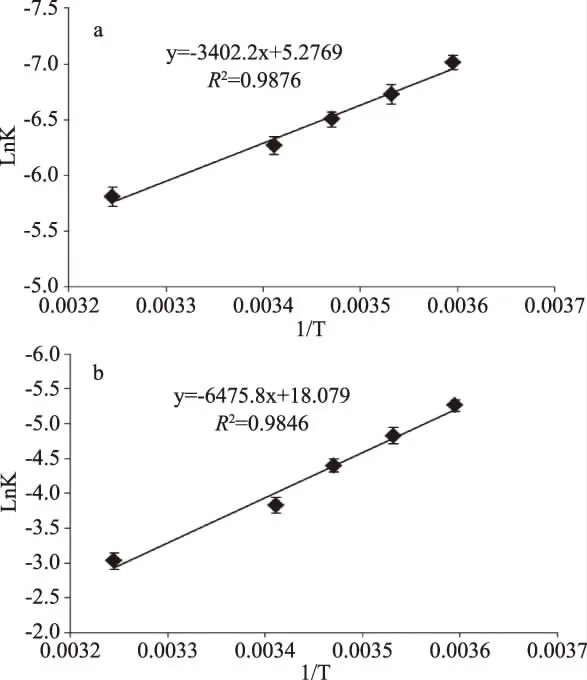
图3 鸡蛋重量、蛋黄系数的Arrhenius曲线Fig.3 Arrhenius curves of weight and yolk index of egg注:a代表鸡蛋重量的Arrhenius曲线;b代表鸡蛋蛋黄系数的Arrhenius曲线。
根据不同贮藏温度下实验数据统计能够得出鸡蛋重量、蛋黄系数的动力学方程,并能结合Arrhenius方程计算出反应速率常数k、A和Ea,可建立鸡蛋重量、蛋黄系数的最终预测模型方程。最终动力学模型方程如式(9)、(10)所示:
鸡蛋重量预测模型方程:
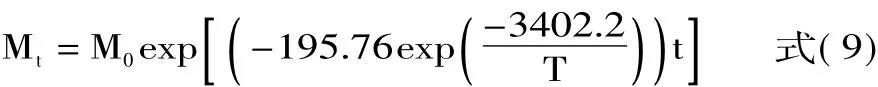
鸡蛋蛋黄系数模型方程:

式中,Mt表示贮藏t时间后鸡蛋重量(g);M0鸡蛋初始重量(g);YIt表示贮藏t时间鸡蛋的蛋系数值;YI0表示鸡蛋初始蛋黄系数。
2.3.2 鸡蛋重量、蛋黄系数的预测模型的验证 用鸡蛋重量和蛋黄系数预测模型方程计算出验证组中25℃条件下鸡蛋的重量和蛋黄系数,即为鸡蛋重量和蛋黄系数的预测值,将其和实测值进行比较(图4(a)、(b))。结果表明,由公式计算得到的鸡蛋重量和蛋黄系数预测值和实测值基于1∶1线的决定系数分别为0.9601、0.9786,根据式(7)计算得出的平均相对误差w分别为0.53%和7.66%,均小于10%,说明模型能较好的预测5~35℃条件下鸡蛋的重量和蛋黄系数。
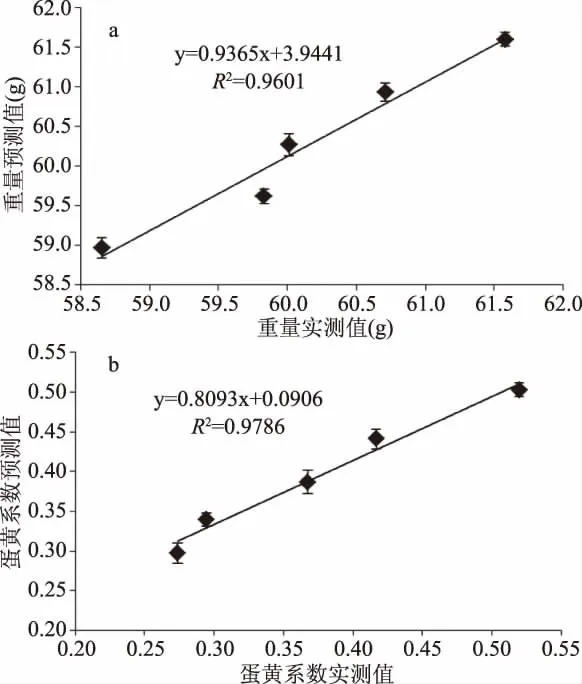
图4 鸡蛋重量和蛋黄系数模型实测值与预测值之间的相关性Fig.4 Correlation between predicted values and actual values of prediction models注:a代表鸡蛋重量模型实测值与预测值之间的相关性;b代表鸡蛋蛋黄系数模型实测值与预测值之间的相关性。
2.4 哈夫单位的预测模型建立与验证
2.4.1 哈夫单位的预测模型建立 根据不同贮藏温度下鸡蛋哈夫单位随时间变化的规律,可以建立哈夫单位随着贮藏时间变化的一级动力学模型。用哈夫单位的回归方程的速率常数对数值(lnk)与对应的温度倒数(1/T)所做的Arrhenius曲线如图5所示,其决定系数为0.9492,这表明本试验选用的一级动力模型跟 Arrhenius方程结合效果较好。由Arrhenius方程计算得到贮藏期间鸡蛋哈夫单位Ea值为4.78×104kJ/mol,A 值为3.95×106。
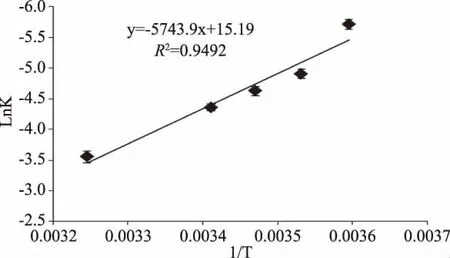
图5 鸡蛋哈夫单位的Arrhenius曲线Fig.5 Arrhenius curves of Hough unit of egg
根据不同贮藏温度下实验数据统计能够得出哈夫单位的动力学方程,并能结合Arrhenius方程计算出反应速率常数k、A和Ea,可建立鸡蛋哈夫单位的最终预测模型方程。最终动力学模型方程如式(11)所示:
气室直径预测模型方程:
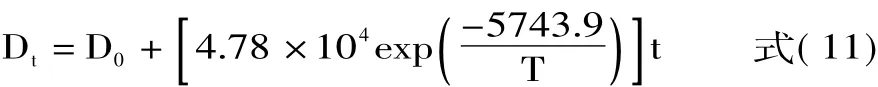
式中,Dt表示贮藏t时间后,哈夫单位值;D0表示起始时刻哈夫单位值。
2.4.2 哈夫单位的预测模型的验证 用鸡蛋哈夫单位预测模型方程计算出验证组中25℃条件下鸡蛋的哈夫单位,即为鸡蛋哈夫单位的预测值,将其和实测值进行比较(图6)。结果表明,由公式计算得到的鸡蛋气室直径预测值和实测值基于1∶1曲线的决定系数为0.991,根据式(7)计算得出的平均相对误差w为2.84%,小于10%,说明模型能较好的预测5~35℃条件下鸡蛋的哈夫单位值。
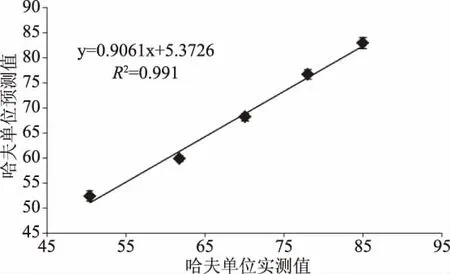
图6 哈夫单位模型实测值与预测值之间的相关性Fig.6 Correlation between measured value and predicted value of Hough unit model
3 结论
本文研究了不同贮藏温度下壳聚糖涂膜鸡蛋的气室直径、重量、蛋黄系数和哈夫单位的动力学模型。研究结果为壳聚糖涂膜鸡蛋的气室直径符合零级动力学模型,重量、蛋黄系数和哈夫单位符合一级动力学模型,且根据建立的模型计算得到预测值与实测值的拟合曲线决定系数R2分别为:0.9797(气室直径)、0.9601(重量)、0.9786(蛋黄系数)和0.991(哈夫单位),并且通过验证平均相对误差w分别为1.95%、0.53%、7.66%和2.84%,均小于10%,表示建立的动力学预测模型方程能较好地描述各指标与温度之间的动力学关系。

