利用微地震事件重构三维缝网

刘 星 金 衍 林伯韬 向建华 钟 华

(①中国石油大学(北京)石油工程学院，北京 102200；②中国石油西南油气分公司，四川成都 610065)

0 引言

随着水力压裂技术在页岩气开发过程中的广泛应用，微地震监测技术逐渐成为实时监测裂缝扩展和压裂效果评价的关键技术[1-4]。但是，目前基于微地震的缝网表征仅能通过事件点推测缝网的宏观参数(如缝网尺度和方位)，从而建立基于一定假设的二维裂缝模型，缺乏压裂改造后三维缝网的重构建模方法。

在水力压裂施工中，在储层中原始裂缝和新生裂缝周围产生不同程度的应力集中，致使总体的应变能增加，当外力进一步增加到临界值时，原始裂缝的弱面中产生微观的屈曲和变形，导致裂缝开始扩展，局部产生应力释放和松弛，储层中的能量以弹性波的形式释放、传播，在地层中产生微地震信号[5-6]。微地震信号以空间事件点的形式被解释、记录，而事件点的空间分布特征和裂缝面存在一定的几何对应关系，这为压裂体积缝网的精细反演和建模提供了数学基础。

在基于微地震事件点的裂缝定量化表征方面，Cai等[7]首次应用微地震监测得到岩石破坏时的事件点密度，并提出了事件点密度和岩石损伤评价指标的关系模型。Sherilyn等[8]通过微地震监测计算的裂缝位置、尺寸、形状等参数校核油藏数值模拟的离散裂缝模型，以提高历史拟合精度。Maxwell等[9]根据微地震事件反映的裂缝位置信息，结合不同裂缝类型的变形机理，模拟了不同的二维平面几何模型的复杂缝网扩展和变形规律。赵争光等[10]通过分析微地震监测过程中事件点的分布和破裂能量，计算了水力裂缝的二维动态延伸和分布范围。Yu等[11]首先对微地震数据进行矩张量分析得到了裂缝的产状参数，进一步结合霍夫变换取得裂缝的形状参数，建立了较为可靠的复杂离散裂缝网络模型。杨瑞召等[12]基于微地震事件点的信号强度数据建立了基于能量层析成像的裂缝反演模型，该模型能得到二维水力裂缝带分布。张云银等[13]利用Delaunay三角剖分算法计算了微地震事件点的空间分布体积，提出了储层压裂改造体积估算方法，可以得到改造缝网体的空间体积。

然而，由于页岩压裂改造后体积缝网的几何形态和空间分布的复杂性，并且监测结果易受环境噪声影响，因此微地震监测事件点中存在噪点[14]。已有的研究大多从定性角度利用微地震事件点分析体积缝网的二维建模，或者利用微地震事件点提取个别裂缝参数以校核基于一定假设的随机离散裂缝网络，但缺乏基于微地震事件的稳健、直接的三维缝网重构方法。本文基于随机模拟一致性(Random Sample Consensus，简称RANSAC)开发了一种稳健的三维缝网重构方法(RFM3D)。首先通过对比室内真三轴水力压裂实验结果建立了随机多边形的单裂缝几何模型，并通过alpha-shape方法开发了基于微地震事件的单裂缝形状识别算法；为了消除事件点中噪点对裂缝重构的影响，采用RANSAC算法提取、计算裂缝面产状，在得到单裂缝的全部信息后通过单裂缝叠加得到RFM3D缝网。为了验证算法的稳健性，利用蒙特卡罗随机模拟方法生成已知缝网，通过对缝网离散生成模拟微地震事件点，在模拟事件点中加入一定比例的噪点后进行RFM3D，以验证算法的稳健性。模拟结果发现，RFM3D算法可在一定程度克服噪点影响，重构缝网与原始缝网符合度较高，具有较高的稳健性。

1 RFM3D原理

1.1 单裂缝几何模型及识别算法

构建离散裂缝网络模型的基础是建立合理的单裂缝几何模型，目前常用的单裂缝几何模型主要有Bacher圆盘模型[15]、改进Bacher圆盘模型[16]、Possion圆盘模型[17]、随机多边形模型[18]等。由于Bacher圆盘模型、Possion圆盘模型与水力压裂中的双翼缝模型较一致，且数值模拟较简便，因此这两种模型得到广泛应用。通过大型真三轴室内压裂实验发现，水力压裂缝网中裂缝的几何形状符合随机多边形模型(图1)，并且随机多边形模型具有表征准确、模型简单、空间变换方便等优点[19]，故本文采用随机多边形模型进行缝网重构。

图1 水力压裂物模实验及缝网描绘

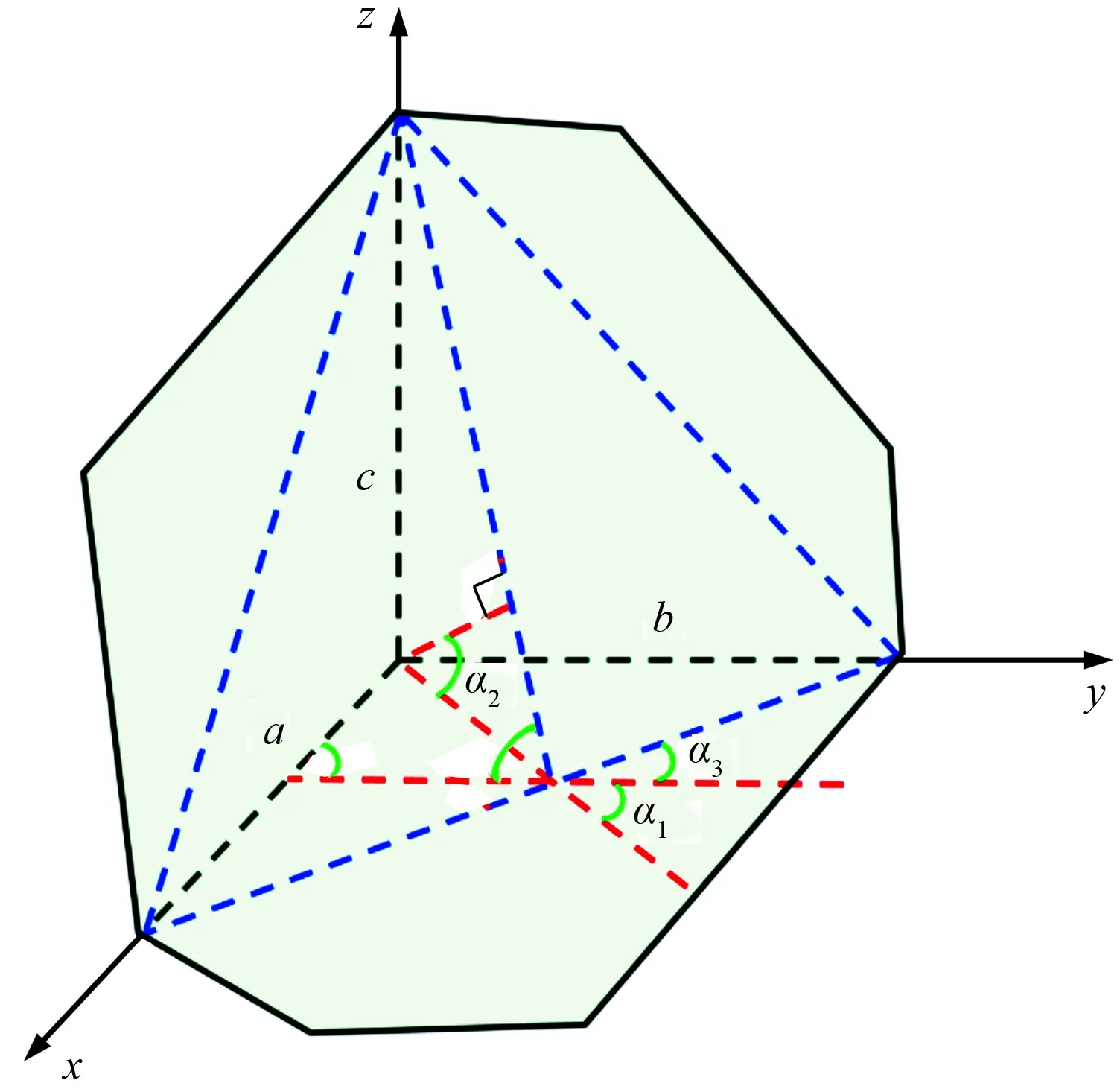
图2 随机多边形单裂缝几何模型

在选择了随机多边形模型(图2)之后，基于裂缝产状三要素(走向、倾向、倾角)构建单裂缝几何模型。假设裂缝的走向为α1、倾角为α2、倾向为α3，裂缝面在三个坐标轴上的截距分别为a、b、c，通过几何关系计算各个产状参数。由截距关系得到裂缝的几何方程为

(1)

裂缝走向为

(2)

其中α1∈[0,π]。同理得到裂缝的倾角为

(3)

(4)

其中α3∈[0,2π]。

在得到裂缝的产状参数之后，根据微地震事件点结合alpha-shape方法开发了三维随机多边形裂缝识别算法[20](图3)，alpha-shape方法是一种Delaunay三角剖分算法。对于一个二维平面上的点集P来说，alpha-shape通过遍历P中的任意两点p和q，当且仅当存在一个以p和q为弦、内部没有其他点的alpha-shape圆盘时，认定p和q为P的二维形状的顶点；在找到所有的顶点后，依次连接所有的顶点形成一个多边形。

图3 alpha-shape形状识别算法示意图

1.2 基于RANSAC的裂缝产状识别方法

在水力压裂施工中，除了周围的噪声源产生的噪点之外，在水力压裂时也会有一部分天然裂缝在诱导应力场的作用下被“激发”，压裂结束后这些处于“激发”状态的裂缝也随即闭合，该部分响应产生的事件点往往距井筒较远，这些额外的事件点和环境噪声形成的事件点形成了微地震监测信号中的“噪点”。对微地震事件点进行RFM3D的首要问题是如何克服噪点的影响、准确地识别裂缝的形状和产状，因此需要选择稳健的回归方法识别、提取裂缝信息。

RANSAC由Fisvhler 等[21]首次提出，主要为了解决被部分噪点污染的数据集的最小二乘估计失真问题。该算法基于随机抽样改进传统的最小二乘法，大大增强了对有效点集的识别，在噪点比例超过10%时仍然能识别有效点集，是一种非常稳健的拟合算法，因此在图像处理领域得到广泛应用。对于单裂缝产状的识别，RANSAC首先将所处理的点集分为噪点和有效点，通过随机抽样挑选一个随机样本；然后使用人为设定的阈值将样本的噪点率控制在合理范围内；最后将选择的样本代入给定的裂缝产状几何方程(式(1))，通过回归得到几何模型的对应产状参数(图4)。

1.3 RFM3D

基于微地震事件得到的位置信息，综合裂缝面产状识别和裂缝形状识别开发了RFM3D(图5)。

结合图4，假设某个含有一定比例噪点的微地震事件点集合为S，其目标缝网中含有m条裂缝，裂缝几何模型为f(x;α)，包含产状和形状参数向量α1,…,αm，RFM3D迭代计算步骤如下。

图4 RANSAC算法识别单裂缝产状示意图

图5 基于微地震数据的RFM3D流程

(1)从微地震事件集合S中随机抽取一个大小为n的样本，并将样本进行裂缝产状模型最小二乘回归得到模型产状参数αtest。

(2)设定距离阈值t，计算剩余所有微地震事件点到该裂缝面的距离，由统计得到在阈值范围内的点集Stest⊆S，当Stest的大小满足要求时，认为选定的点集符合裂缝的拟合条件。

(3)重复步骤(1)，再次随机选择一个大小为n的样本，得到阈值范围内的标识点集Sin和产状参数标识向量αc，如果|Sin|<|Stest|，令Sin=Stest，则αc=αtest。

(4)设定点集阈值为T，重复步骤(1)～(3)，直到|Sin|≥T为止，经统计得到总迭代次数N，进而得到首个单裂缝产状参数向量α11=αc，并将Sin代入alpha-shape形状识别算法，得到裂缝的形状参数向量α12，通过组合得到首个裂缝几何模型的全部产状和形状参数向量α1。

(5)从原始事件点集S中去除Sin得到剩余微地震事件点集Sres，对Sres重复步骤(1)～(4)得到第二个裂缝模型的全部参数向量α2。

(6)重复步骤(1)～步骤(5)m次，直止得到所有裂缝的几何参数向量α1,…,αm，算法运行结束。

在随机抽样过程中，如果p表示在N次抽样中至少有一次抽到完全没有噪点的样本的概率，那么可以得到迭代次数N

(5)

式中：p为成功抽到完全为有效点样本的概率；ω为有效点占所有事件点的比例；n为每次随机抽样的样本大小。

式(5)表明，随着ω的减小、n的增大，迭代次数随之增加。但是在实际微地震监测中一般很难得到确切的噪点比例(噪点个数与有效点的比值)，因此也无法得到准确的迭代次数N，可以采取估计的方式近似用每次得到的标识点集的大小和事件点集大小的比值作为每一次迭代过程的ω，根据每次的计算结果调整总的循环迭代的上限N，可以在大规模缝网重构中有效减少计算时间，提高计算效率。

2 模型稳健性定量分析

2.1 模型稳健性模拟分析

为了验证RFM3D算法的稳健性，采用蒙特卡罗方法生成裂缝数量为5、10、15、20的四种模拟缝网，采用随机离散的方法将模拟缝网离散为模拟微地震事件点集，加入一定比例的、由均匀随机过程生成的噪点，通过对模拟离散微地震事件点进行RFM3D得到新缝网，通过对比原始模拟缝网和重构缝网分析算法的稳健性。

图6为不同裂缝数目m的缝网模拟结果。由图可见，RFM3D能很好地克服噪点影响，重构缝网和模拟缝网的相似度较高，算法具有较好的稳健性。

图7为裂缝数目为10的不同噪点比例的RFM3D结果。由图可见，在保持缝网不变的条件下，对原始缝网离散化处理后(图7a)，分别添加5%(图7b)、10%(图7c)、15%(图7d)、20%(图7e)、25%(图7f)的噪点比例进行RFM3D。模拟结果表明，随着噪点比例增加，RFM3D缝网(图7b～图7f)与原始缝网(图7a)相似性降低，重构效果逐渐变差，并且当噪点比例大于10%时(图7d～图7f)，RFM3D缝网的不确定性明显增加，当噪点比例不大于10%时(图7a～图7c)，RFM3D效果较好，表明RFM3D算法可以克服约10%的噪点影响，该结果在后续的模拟中会得到进一步证实。

图6 不同裂缝数目m的缝网模拟结果(噪点比例均为10%)

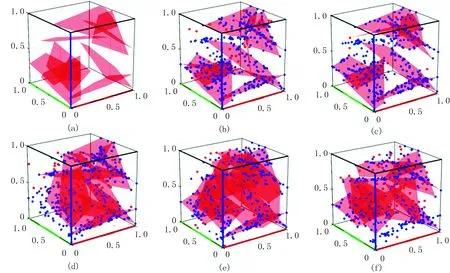
图7 裂缝数目为10的不同噪点比例的RFM3D结果

2.2 模型鲁棒性分析方法

为了定量分析RFM3D算法对噪点的稳健性(图6a)，首先使用蒙特卡罗方法在1m×1m×1m的立方体中随机生成模拟缝网，结合测绘学空间形状相似性理论[22]，提出了基于单裂缝的平均距离的相似性指标ADI(Average Distance Index)。

如图8所示，以多边形单裂缝ABCD和单裂缝A′B′C′D′为例，采用“五点法”计算ADI，其方法是寻找两个缝网中的裂缝对应关系，然后通过计算五点对应距离的平均值作为两个裂缝的ADI(图6)，最后求取模拟缝网和重构缝网所有裂缝的ADI均值作为缝网ADI，其计算步骤如下：

(1)假设模拟缝网和重构缝网的个数均为m，首先确定两种缝网的单裂缝对应关系，形成m个裂缝对。

(2)分别计算第i个裂缝对的顶点平均距离Lfi和裂缝中心点的距离Dfi。

图8 多边形裂缝相似性度量示意图

(3)重复步骤(1)～(2)遍历所有裂缝对，得到重构缝网和模拟缝网的平均单裂缝ADI

(6)

由式(6)可知，在一定的噪点比例下，ADI的范围为0～1，其中缝网ADI越大，重构缝网和模拟缝网间的差异就越大，RFM3D的重构效果越差；反之，缝网ADI越小，重构缝网和模拟缝网越接近，RFM3D的效果越好，其中ADI=0表示重构缝网和原始缝网完全重合。根据ADI的不同取值范围对应的噪点比例定义为第一、第二和第三临界点，并且以此划分了四个评价区间，据此给出了四种重构效果(较好、一般、较差、最差)(表1)。通过设定不同的噪点比例和裂缝数目进行模拟，以缝网ADI所在区间定量评价算法的重构效果。

表1 ADI评价区间划分结果

2.3 缝网相似性模拟分析

在定量评价RFM3D算法的稳健性过程中，其核心是通过蒙特卡罗生成模拟缝网样本，计算不同噪点、不同裂缝数目的ADI。图9为RFM3D算法噪点比例—ADI曲线。由图可见：①随着噪点比例增加，ADI基本上落在0～0.5范围，虽然由于随机抽样的原因致使计算结果略有波动，但ADI总体呈非线性增长，表明RFM3D效果越来越差，噪点对重构结果的影响也越来越大，重构缝网的不确定性增加。②即使模拟缝网中裂缝数目不同，ADI值在噪点比例大于200%时达到最大并保持稳定，表明重构缝网和原始缝网的相似性较差，说明当原始微地震事件点集中时若噪点比例高于200%，有效点集完全被噪点淹没，重构缝网也完全失真，不具有参考价值，即将200%作为RFM3D算法的噪点比例上限。③对噪点比例—ADI曲线进行非线性回归发现，ADI随噪点比例满足logistic增长模式(缝网ADI先增加后减小并趋于零，中间存在增速极值点，并且极值点位于第二临界点附近)。因此对于一个特定微地震事件点的降噪处理来说，需要将噪点比例至少降低到第二临界点以下，重构缝网形态才会逐渐趋于稳定，若将噪点比例降低到第一临界点以下才能得到较为可靠的重构结果。④噪点比例—ADI曲线随着裂缝数目的增加逐渐变得陡峭，ADI增长速度明显加快，并很快趋于稳定，说明在同等条件下裂缝数目越多，噪点对算法的影响越大，需要将噪点比例降至更低才能得到可靠的重构结果。

图10为m—噪点比例曲线。由图可见：①第一临界点随着裂缝数目m增加呈下降趋势，在m=1以后趋于稳定，并且噪点比例稳定在约10%，即使裂缝数目进一步增加，第一临界点也几乎保持不变。由于当噪点比例小于第一临界点时RFM3D结果是稳定、可靠的，因此RFM3D算法的噪点比例下限为10%，说明在一般条件下对不同裂缝数目的缝网重构来说，RFM3D算法至少可克服10%的噪点影响，这和前文的不同噪点比例的RFM3D结果一致(图7)。②随着裂缝数目增加，三个临界点的值也逐渐减低，表明裂缝数目越多，RFM3D重构效果越差，当m=9时，第三临界点降低到50%以下，说明在使用RFM3D算法重构含有较多裂缝的目标缝网时需将噪点比例降至更低，否则无法得到可靠的结果。

图9 RFM3D算法噪点比例—ADI曲线

设定噪点比例范围为0～200%(步长为2%)，缝网中裂缝数目分别为3、5、7、9、10(步长为2)，编写MATLAB程序对每种缝网进行100次RFM3D，分别计算重构缝网和模拟缝网的ADI

图10 m—噪点比例曲线

2.4 模型稳健性定量分析

综上所述：RFM3D算法是一种较稳健的缝网重构方法，且ADI随噪点比例呈logistic曲线增长；在一般条件下，RFM3D算法的噪点比例下、上限分别为10%、200%；随着裂缝数目增加，RFM3D算法受噪点的影响越来越严重。因此，在使用RFM3D算法重构大规模的缝网时必需对微地震事件点进行降噪处理，使噪点比例控制在10%以下，才能得到稳定、可靠的缝网重构结果。

3 工程应用分析

3.1 工程地质背景

YY1井位于川中隆起区的川西南低陡褶带，钻遇志留系龙马溪组页岩储层，平均孔隙度为5.28%，基质渗透率均值分布范围为(4～5)×10-5mD，含气孔隙度平均值为2%，含气饱和度平均值约为50%，总体上储层物性较好。井下成像测井和岩心资料表明，YY1井中的天然裂缝主要为构造裂缝以及超压填充裂缝，其中构造裂缝形成的张开缝多为高角度垂直缝，超压裂缝多为微细裂缝，空间呈网状分布，延伸距离较小，大多数被矿物充填(图11a)；该区最大水平主应力方位约为135°(图11b)，YY1井所在地区天然裂缝总体发育方向(图11c)与该区最大主应力方向夹角较大，在水力压裂过程中地应力使高角度天然裂缝闭合，因此不利于天然裂缝的张开[23]。由YY1井三个压裂段微地震监测结果(图12 )可见：①由于地应力的屏蔽作用，未出现远井天然裂缝的激发响应产生的微地震事件点，均匀分布的事件点有利于RFM3D，在一定程度上降低了的影响，事件点沿井分布较为集中，未出现高导流的长段水力裂缝，并且在3个施工段分布相对均匀；④对于每一级压裂来说，平均缝长和平均缝宽约为200m。为了评估YY1井压裂效果，对YY1井的微地震事件点进行RFM3D，并结合地应力和天然裂缝分析结果对RFM3D结果进行对比、验证。

图11 YY1井地应力方位和裂缝方位[24]

图12 YY1井三个压裂段微地震监测结果

由孤立事件点引起的误差；②YY1井微地震监测为3级接收，现场实时处理并定位的有效微地震事件点共1800个；③从微地震事件震级及分布特征看，事件在压裂施工全程均有发生，受地应力屏蔽作用

3.2 RFM3D结果分析

由微地震监测结果(图12)和RFM3D结果(图13)可知，水力压裂形成了一定规模的体积缝网；由裂缝与微地震事件对比图(图13b)可见，重构的三维缝网和原始微地震事件贴合度较高，每个压裂段重构的裂缝延伸范围仅限于该压裂段对应的微地震信号的展布范围。由于水平最大地应力方向和天然裂缝的夹角较大，因此天然裂缝对水力裂缝的延伸具屏蔽作用，造成水力裂缝的延伸范围仅限于井筒周围，未出现远井区域的孤立微地震事件点，同时也未出现个别的高导流水力裂缝，整体上微地震事件和压裂裂缝沿井分布较为均匀。

图14为YY1井三维缝网产状分布。由图可见：

图13 YY1井RFM3D结果(a)及裂缝与微地震事件对比图(b)

图14 YY1井三维缝网产状分布

水力裂缝的优势走向范围为120°～150°，平均值为135°，垂直井筒并与水平最大地应力方向一致，RFM3D结果和由地应力分析得到的水力裂缝扩展方向一致；裂缝的倾向集中在240°，与最大主应力方向垂直；裂缝的优势倾角范围为60°～90°，表明裂缝经压裂改造后主要为高角度垂直缝，与成像测井分析结果一致，说明井筒周围的天然裂缝对水力裂缝的起裂和扩展具重要影响。总体来看，重构后的缝网和水力压裂实验中的裂缝扩展规律一致[25]，验证了RFM3D算法的可行性。

4 结束语

本文基于随机模拟一致性和alpha-shape方法开发了页岩压裂体积缝网重构算法(RFM3D)，通过蒙特卡罗缝网模拟定量分析了算法对噪点的稳健性，并用于川中地区YY1井的微地震缝网重构，得到以下认识：

(1)通过室内压裂实验发现，可用随机多边形模型描述实际裂缝形状。

(2)RFM3D算法易于匹配复杂的裂缝几何模型，在一般条件下该算法至少能克服10%的噪点干扰，可较准确地重构压裂缝网的几何形态，算法具有较好的稳健性。

(3)随着噪点比例增大，重构相似性指标(ADI)随噪点比例满足logistic增长模式；随着缝网中裂缝数目的增多，ADI临界点也随之降低。因此，在重构大规模体积缝网时噪点比例应严格控制在10%以下才能得到稳定、可靠的结果。

对于页岩压裂体积缝网重构算法来说，裂缝数目和噪点比例是影响缝网重构精度的主要因素。本文从微地震点和裂缝面的几何关系出发，提出了一种较为可行的重构方法，该研究也可用于基于缝网的页岩产能预测和储层改造体积的计算。