球面距离计算方法及精度比较*

樊东卫，何勃亮，李长华，韩 军，许允飞，崔辰州

(中国科学院国家天文台，北京 100101)

平面距离只需要计算连接两点线段的长度，通过二维直角坐标使用勾股定理可以很容易地计算出来。由于只涉及乘法、加法与开平方运算，在计算机中也可以保留很高的精度。而球面距离计算则要复杂得多。球面在直角坐标系中实际上是三维结构，除非距离相对于半径非常小，否则不能当作平面处理。

两点球面距离计算是天文或地理学中最常用的计算之一，是目标查找、锥形检索、交叉证认等计算中最基础的运算。比如查找距离某个位置最近的山峰，需要先对附近的山峰都计算一遍距离，取出距离最小的一个。而锥形检索是虚拟天文台的数据检索协议之一，用于在球面上查找与某点的距离小于指定半径的目标列表，几乎所有提供了星表查询功能的系统都有类似功能[1]。基于位置的星表交叉证认则可视为对一个星表A中所有的源做一遍锥形检索取得与其最近的另一星表B的源，这样就完成了A，B两个星表的交叉[2]。这些应用的基础都是球面距离计算。

两点球面距离计算，计算的是两点在球面上的最短距离，即球心与两点组成的大圆上两点之间较小的那段圆弧的长度，天文上习惯使用该短圆弧对应的大圆圆心角，称为角间距(Angular Separation)或角距离。球面距离需要使用球面几何进行求解，要大量使用三角函数。而计算机的数值计算精度有限，在对三角函数、反三角函数进行计算时容易出现舍入误差。多个函数的误差积累之后，将导致严重的结果偏离，甚至无法得到正确的结果。前人已经推导了很多数学公式求解球面距离，但在何种情况下使用哪个公式，公式的精度如何，却鲜有人讨论。因此，本文考察天文技术中常用的球面距离计算公式，给出它们的算法，并对比它们的精度，为球面距离算法的选择提供参考。

1 球面几何方法

球面距离计算可直接通过球面几何推导。较常用的计算公式有大圆(Great-circle)公式①https：//en.wikipedia.org/wiki/Great-circle＿distance、Haversine公式②https：//en.wikipedia.org/wiki/Haversine＿formula等。另外还有Vincenty公式③https：//en.wikipedia.org/wiki/Vincenty%27s＿formulae被应用到Astropy等代码库中，但其复杂度过高，本文在第3.1节中简要提及。

设有两点赤道坐标为p1(α1，δ1)，p2(α2，δ2)，求它们的球面角距离d。其中大圆公式为(1)式；当两点距离很小时，也有人使用简化的(2)式[2-6]；Haversine公式如(3)式。

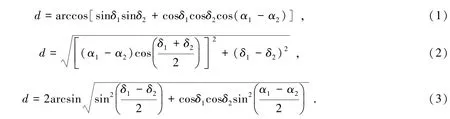
计算机中通常使用IEEE754二进制浮点数算术标准处理浮点数，其中单精度32位(float或single)真值可精确到小数点后6～9位，双精度64位(double)真值可精确到小数点后15～17位④https：//en.wikipedia.org/wiki/Single-precision＿floating-point＿format。本文使用C＋＋语言编写程序对3个公式的精度进行了对比，结果如表1。本文使用的单位均为度(°)，表中有两行数据时，上方的值为单精度计算的结果，下方的值为双精度计算的结果。

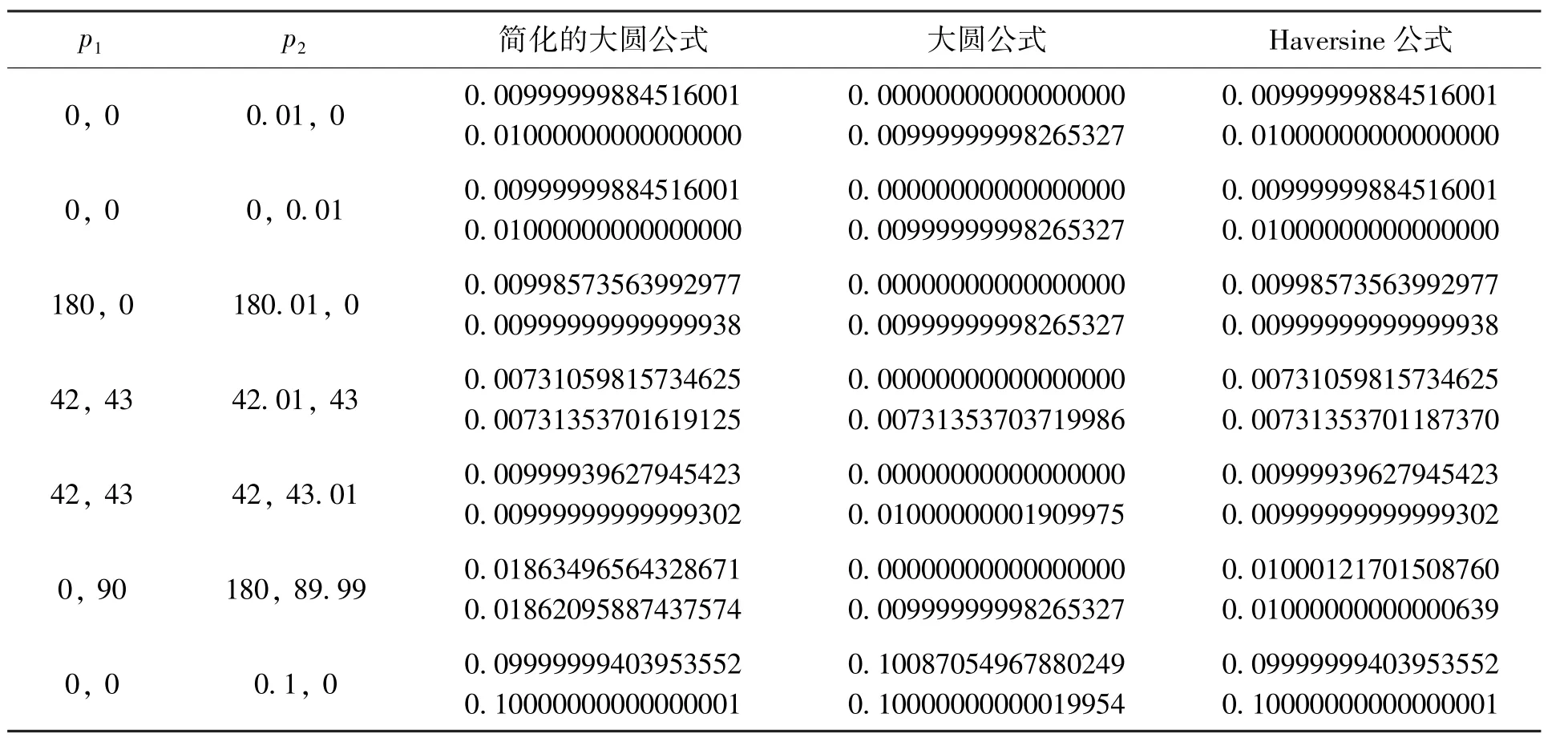
表1 使用不同的点测试常用球面距离公式的精度(单位：度)Table 1 Accuracy testing at different points for widely used formulas(unit： degree)

由表1可见，单精度下，两点之间距离较近时，大圆公式返回的是全0，出现了严重的舍入误差，而距离较大时误差也较大。双精度下，大圆公式能够返回结果，但比Haversine公式的精度要差。大圆公式的简化形式多数时候与Haversine公式的精度相当。这3个公式共有的一个问题，它们均有可能略微超过准确值，当严格限定一个边界值的时候，可能导致漏源。因而在实际应用时，需要考虑将边界值略微外扩，以将因为计算精度而漏掉的源包含在内。

值得注意的是，大圆公式的简化形式在极点附近时误差非常大。虽然它在上述公式中是计算复杂度最低的，并且在两极之外、距离较小时精度与Haversine公式相近，但是在实际使用该公式时仍应当非常小心。

2 直角坐标系方法

在基于赤道坐标系进行求解之外，也可以使用直角坐标系，通过三维坐标向量对两点球面距离进行计算。可视天球半径为单位1，以天球球心为三维直角坐标系原点，赤道坐标系北天极点方向为z轴方向，天赤道面上赤经为0点的方向为x正向，遵循右手坐标系与x-z相交的轴为y轴方向。从而可将赤经、赤纬转换为三维直角坐标(x，y，z)，其转换关系如(4～6)式⑤https：//arxiv.org/abs/cs/0701171。

这样两点距离计算可以直接使用(8)式进行计算。该公式可简单地从Haversine公式中推得，其中Haversine公式根号中的部分(7式)实际上是两点的三维空间直线距离一半的平方。

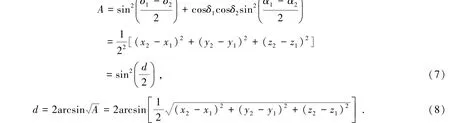
直角坐标系的计算精度方面，本文依旧使用C＋＋语言在单精度及双精度两种环境下对公式进行计算，并与Haversine公式的结果对比，结果如表2。从表2可以看出，直角坐标系方法的精度与Haversine公式几乎完全一致，而直角坐标系方法有时甚至优于Haversine公式(见42，43两行数据)。

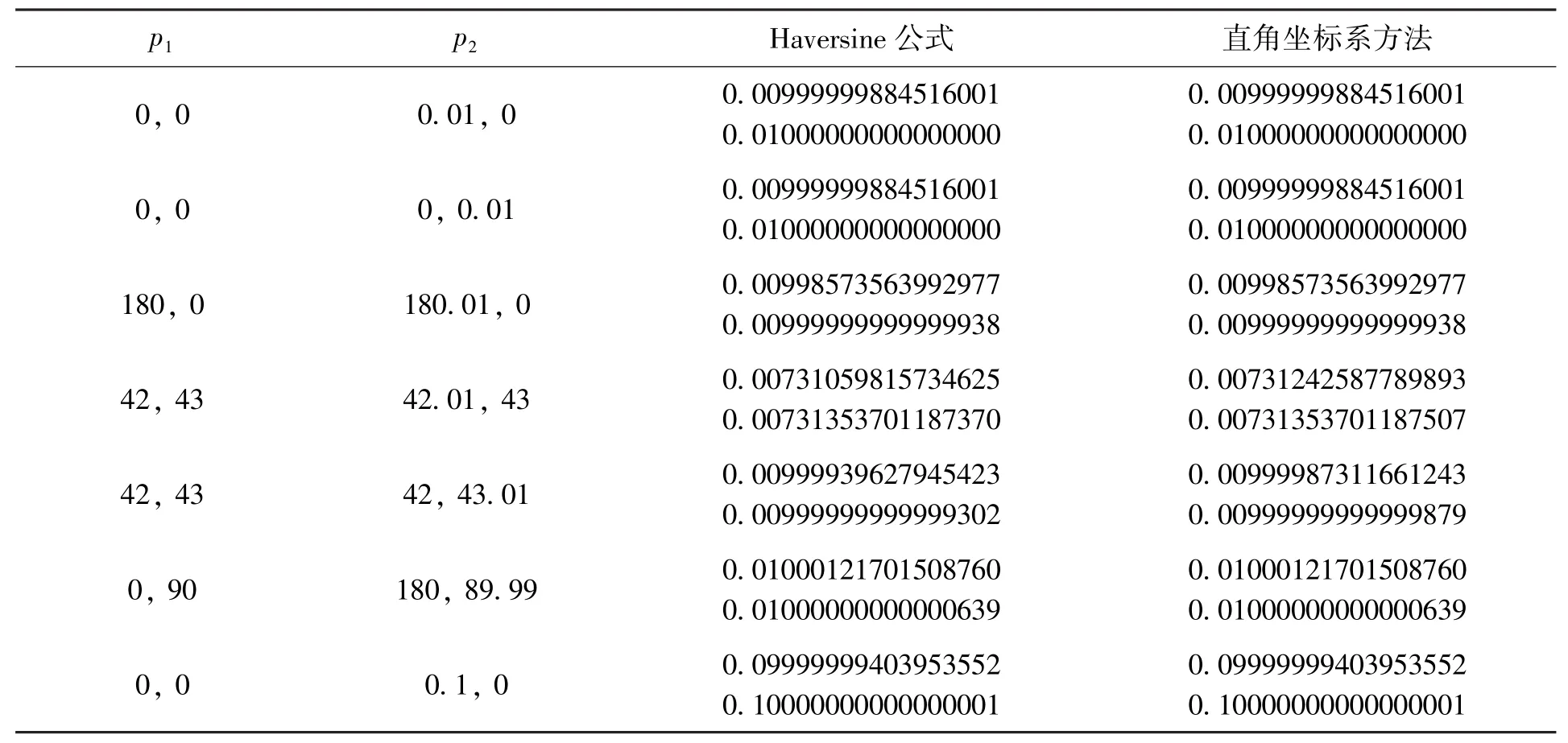
表2 Haversine与直角坐标系计算结果对比(单位：度)Table 2 Result comparison between Haversine and Cartesian method(unit： degree)

直角坐标系方法在进行距离比较时还可以进一步优化，如(9)式：设两点直角坐标为p1(x1，y1，z1)，p2(x2，y2，z2)，其优点是可以预先计算x，y，z与threshold(设最大角距离为θ)，从而避免在实际进行距离计算时使用非常耗时的三角函数，而只需要三次减法、三次乘法、两次加法、一次比较，大大减少了计算量，非常适用于大规模数据计算。相应地，它的缺点是需要额外占用存储空间来保存x，y，z三个值，在对内存占用要求较苛刻的环境中可能会成为问题。因而，实际的公式选择，仍应视数据规模、计算环境而定。另外，基于三维向量的计算方法，还有法线向量的形式，但其计算过程比本节要复杂，本文将在第3.3节中进行简要描述。

3 计算库

许多天文软件包也包含了球面距离计算功能。本部分选择了几个安装、使用较便捷，应用也比较广泛的库，演示了其使用方法，并进行测试。由于难以分辨软件包中实际使用的是单精度还是双精度，此部分不再对此进行区分，而直接与Haversine双精度结果进行比较。

3.1 Astropy

当前天文界已经非常流行使用Python进行数据处理，其中Astropy[7]对Python的推广传播功不可没。Astropy进行球面距离计算需要使用astropy.units及astropy.coordinates.SkyCoord计算。调用方法如下，其中d为两点之间的角距离(单位是度)：

为公平起见，在64位Windows10中的64位python3.6.3重新实现了Haversine算法，并与Astropy的距离计算函数进行了对比，对比结果见表3，可以看到两种方法基本一致，不分伯仲。

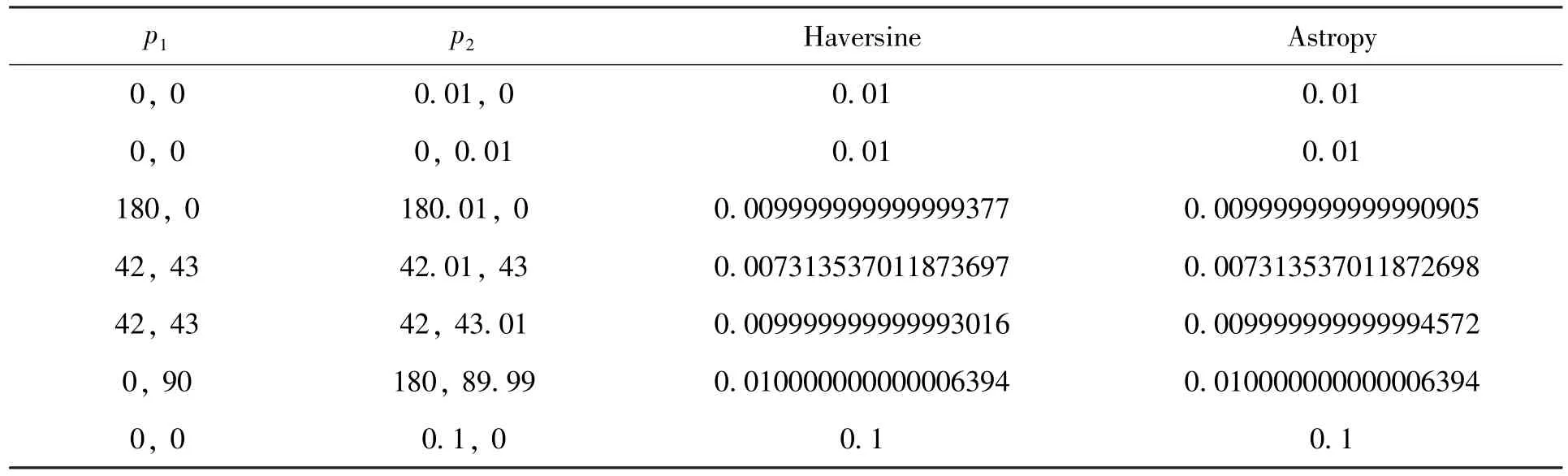
表3 Windows 64位Python3环境下Haversine与Astropy计算结果对比(单位：度)Table 3 Result comparison between Haversine and Astropy on Windows 64bit Python3(unit： degree)

阅读Astropy的源代码可发现其距离计算函数separation实际调用的是astropy/coordinates/angle＿utilities.py⑥https：//github.com/astropy/astropy/blob/master/astropy/coordinates/angle＿utilities.py中的angular＿separation(lon1，lat1，lon2，lat2)函数，其代码实现使用Vincenty公式，即(10)式。该式在所有位置的距离计算都更稳定，但计算复杂度也更高[8]。从上述计算对比结果来看，Astropy并没有处处比Haversine的精度更高，如(180，0)一行；当然，Astropy在(42，43)上的精度也比Haversine更好。但是两者的差距都非常小，几乎可以忽略不计。从比较结果上看，Haversine已经相当精确。当然，若是对计算稳定性有更高要求，可以考虑Vincenty公式。

3.2 分层三角网格

分层三角网格(Hierarchical Triangular Mesh，HTM)[9]是一种对球面的多层次、递归三角分割方法。分层三角网格目前公开提供下载的软件包⑦http：//www.skyserver.org/htm/index.html中包含了C＃代码库及一个SQL Server扩展包。其中Spherical.Htm.Sql.cs文件中包含了函数fDistanceEq(ra1，dec1，ra2，dec2)，可用于计算距离。需要注意的是，fDistanceEq的返回值单位是arcmin，不是degree。针对分层三角网格，本文使用C＃实现了Haversine函数并与SphericalHTM v3.1.2的fDistanceEq函数进行对比。如表4，其结果基本相同。查看源代码发现fDistanceEq实际上也使用了Haversine公式进行计算，只是多了degree到arcmin的转换。

除了C＃程序中可以直接调用fDistanceEq外，HTM软件包提供的SQL Server数据库扩展包中也带有此函数，在数据库中使用非常方便。

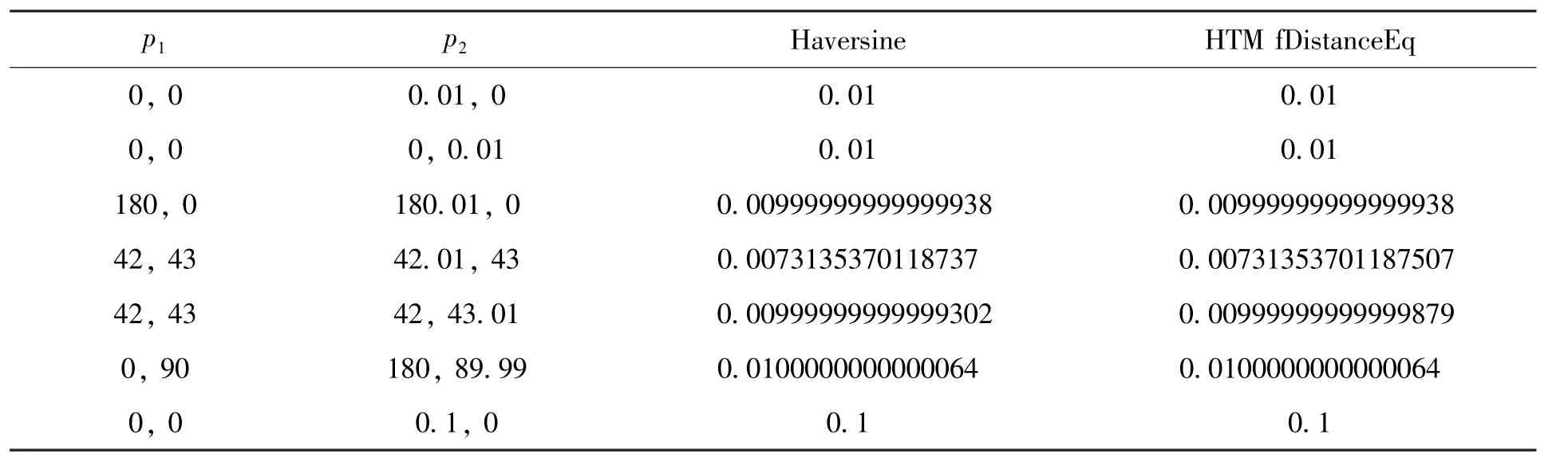
表4 C#环境下Haversine与HTM fDistanceEq计算结果对比(单位：度)Table 4 Result comparison between Haversine and HTM fDistanceEq on C#(unit： degree)

3.3 SLALIB与SOFA

SLALIB即Starlink library of positional astronomy routines⑧http：//stsdas.stsci.edu/cgi-bin/gethelp.cgi?slalib.sys，使用Fortran 77实现，其目标是让天文工作者更简便快捷地编写精确可靠的天体测量程序。虽然它是由Fortran 77实现的，但是已经有人为其编写了Python接口pyslalib⑨https：//github.com/scottransom/pyslalib，因而可以在已有的Python环境中获得Fortran 77的计算精度。

Pyslalib中的slalib.sla＿dsep直接对应了SLALIB中的sla＿DSEP(A1，B1，A2，B2)球面距离计算函数，在64位的Ubuntu 16.04.4操作系统中使用64位 Python3.5.2环境将其与Haversine函数的计算结果进行了对比，如表5。首先可以看到Linux版的Python Harversine程序计算结果与Windows一致，表明Python3在不同的操作系统中的表现一致。其次pyslalib的计算结果，除了(42，43)两行有轻微差别，与Haversine完全一致，精度也非常高。查看SLALIB的源代码，可以看到其使用了第2节中的直角坐标系三维向量作为计算单元。但与第2节不同，SLALIB进一步将其转换为法线向量⑩https：//en.wikipedia.org/wiki/N-vector，即与，再使用(11)式[10]进行计算。使用向量的主要优势是向量代数可取代部分三角函数的计算，其数值计算稳定性更好，能保持较好的精度，并且在边界点(如南北天极、0～360度边界)也无异常。

天体测量中常用的SOFA库⑪http：//www.iausofa.org的球面计算函数iauSeps⑫http：//www.iausofa.org/2018＿0130＿C/SeparationPA.html也同样使用了(11)式。SOFA即Standards of Fundamental Astronomy，是国际天文学联合会建立并维护的一个权威的基本天文学标准库，包含有ANSI C及Fotran 77两个版本。表5的最右侧列出了双精度位C＋＋程序调用SOFA计算的结果。

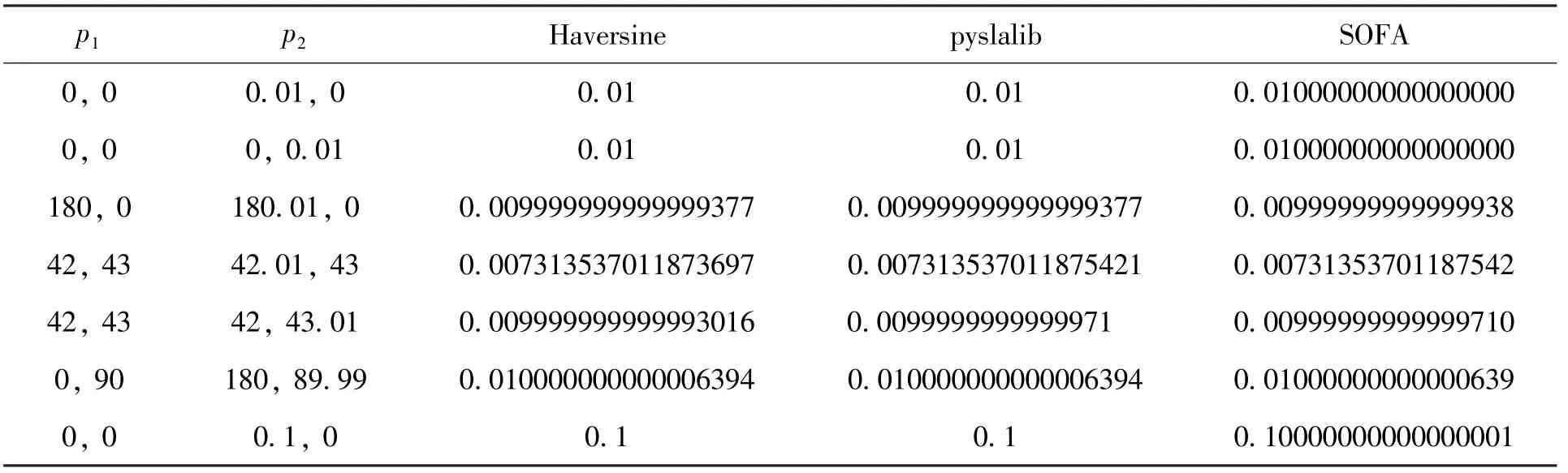
表5 Linux 64位Python3环境下Haversine与pyslalib及双精度C++版本SOFA计算结果对比(单位：度)Table 5 Result comparison among Haversine and pyslalib on Linux 64bit Python3 and double precision C++version SOFA(unit：degree)

4 数据库

关系型数据库均支持SQL语句，因而可以在不同的系统中直接使用SQL语句实现Haversine公式进行距离计算。由于每种数据库使用的数学函数、计算精度略有差别，本文在Microsoft SQL Server 2008，PostgreSQL 9.4.5，MySQL 5.7.18上进行了测试，测试结果如表6，从表6可以看到，3个数据库的差距不大，MySQL默认保留的精度更多一些。

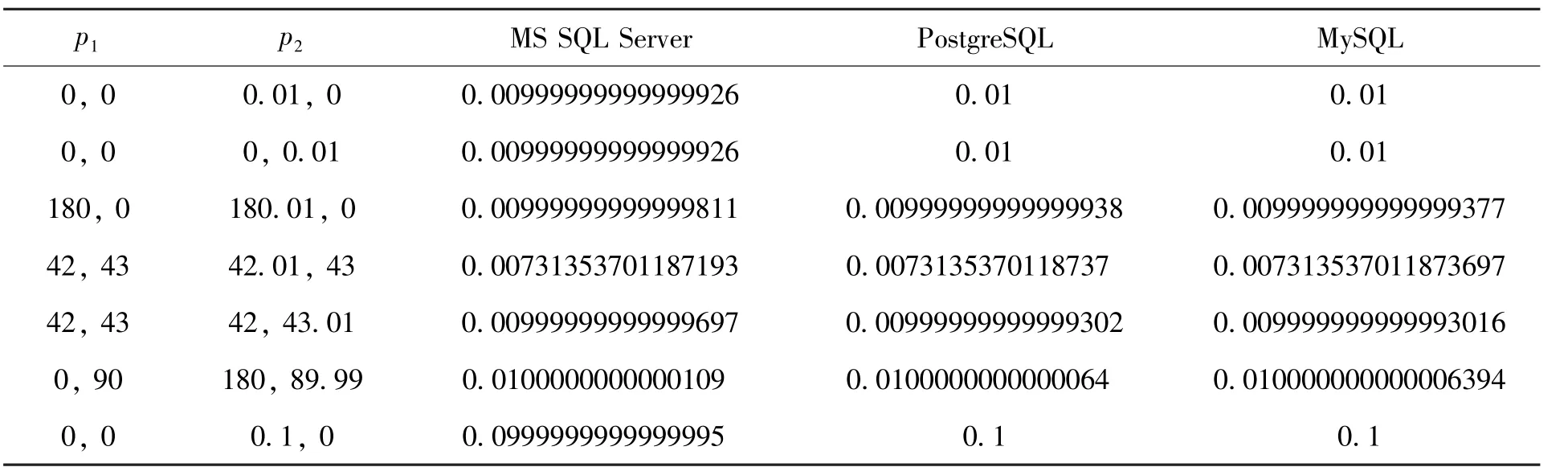
表6 不同数据库中使用Haversine公式计算距离的精度对比(单位：度)Table 6 Accuracy testing for pure SQL Haversine on different database(unit： degree)

除了Haversine公式，数据库中使用直角坐标系方法实际上更方便。数据库对I/O进行了大量优化，可以更好地对数据进行调度。因而，直角坐标系方法虽然需要增加x，y，z 3个字段，但并不会给数据库增加太大的负担，还可以大大降低计算的复杂度，更快地取得海量数据的计算结果。

4.1 PostgreSQL数据库插件

数据库中除了可以直接使用公式之外，也可以使用各种数据库扩展插件进行相关计算，减少使用者编程的麻烦。 如 PostgreSQL 数据库有 PostGIS⑬https：//postgis.net/， pgsphere⑭https：//github.com/akorotkov/pgsphere， Q3C⑮https：//github.com/segasai/q3c， H3C⑯http：//cds.u-strasbg.fr/resources/doku.php?id＝h3c等多个插件支持球面距离计算。其中PostGIS是专为地理信息系统设计的，虽然也可以在天文上使用，但是需要将米、千米等单位转换回弧度，太过繁琐低效。而pgphere，Q3C[11]，H3C则是专门为天文检索设计的，更为简洁。下文演示了3种插件的使用方法，表7对这3个插件的结果进行了对比。需要注意的是Q3C和H3C直接使用度进行计算，而pgsphere需要先转成弧度进行计算，再将结果转回角度。

表7 PostgreSQL数据库Q3C，H3C，pgsphere插件的球面距离计算精度比较(单位：度)Table 7 Accuracy testing for different PostgreSQL extensions(unit： degree)

从三者的结果来看，精度大抵相当，没有太大差距，在极点的计算也都没有太大的偏差。经阅读源代码，可以看到h3c＿dist函数使用了Haversine公式，q3c＿dist函数使用了Haversine的一种变体，pgsphere的情况则较为复杂，它在距离大时使用大圆公式，距离较小时使用直角坐标公式。从计算结果来看，这3个插件都不失为成熟可用的扩展，具体要使用哪个，还要看其他的需求。如Q3C，H3C均提供了join函数(分别是q3c＿join，h3c＿join)，对两星表交叉证认进行了优化。而pgsphere提供了丰富的球面几何计算，如球面形状的面积计算，球面形状的交、并计算等。

5 总 结

本文探讨了大圆公式、简化的大圆公式、Haversine公式等球面距离计算方法，并对比了它们在计算机中进行单精度及双精度数值计算的结果。在此基础上，引申出了基于三维直角坐标系的距离计算方法。结果表明大圆公式在单精度下舍入误差非常严重，而大圆公式的简化公式在两极或两点距离较大时误差很大。Haversine公式与直角坐标系方法的精度相近，都非常高，而直角坐标系方法的计算量较小，适合大数据的计算。此外，还需要注意所有这些公式在计算时，有时候计算结果会略微大于准确值。因而在实际应用时，可能需要将边界值取得略大一点，以将因为舍入误差漏掉的源包含在内。

已有软件包如Astropy，HTM，SLALIB，SOFA以及部分数据库扩展也将球面距离计算模块包含在内。它们所使用的计算方法不尽相同，结果精度也非常高。当需要进行球面距离计算时，可以直接使用这些库，而无须自行实现过于复杂的公式，以免重复工作且易因考虑不周而导致出错。