基于状态识别的经验模态分解法火电厂运行数据预处理
赵 悦,方彦军,董政呈
基于状态识别的经验模态分解法火电厂运行数据预处理
赵 悦,方彦军,董政呈
(武汉大学动力与机械学院,湖北 武汉 430072)
针对火电机组运行监测数据量大且复杂情况下的去噪问题,提出一种基于状态识别的改进经验模态分解去噪(SREMD)算法。该算法以经验模态分解(EMD)方法为基础,首先运用基于拉伊达(Pauta)准则的滤波方法去除显著异常数据,然后根据数据连续变化率动态识别机组运行状态,最后根据机组运行状态的稳态过程和过渡过程分别进行针对性EMD去噪,以适应火电机组的状态切换特性。将该算法用于实际机组运行数据,结果表明,本文算法有效完成了火电机组监测数据的去噪预处理,在保持信号整体趋势的基础上能达到更好的去噪效果。
火电机组;数据预处理;去噪;滤波;Pauta准则;EMD;状态识别
火电机组运行数据是由现场成千上万个传感器获得,这些传感器实际工作环境复杂,很多传感器在高温、高压等极端条件下工作,其精度会受到影响,出现故障的概率也较大。此时传感器采集到的数据就会存在各种异常值,若对这些数据不做相应的预处理,后续数据的使用就会受很大的影响。因此,采集数据需进行异常值检测、噪声剔除等数据预处理操作。
火电机组运行数据具有如下特点:1)测量点多,数据量庞大;2)测量环境复杂多样,数据夹杂大量噪声;3)数据类型多样,具有较强的动态性[1-3]。传统数据预处理方法直接应用于电厂运行数据预处理时会出现很多问题,达不到预期效果。如常用的量程检测法,只可识别出少量的异常数据;简单滤波算法只可剔除少量误差较大的噪声数据。而大部分的大数据预处理方法不能直接用于电厂大数据的预处理,当前关于电厂运行数据的大数据分析侧重于参数研究、运行优化等方面[4-11],对电厂数据的滤波去噪等针对性预处理的研究则较少。
一些新的数据预处理方法被提出:文献[12]采用SSD(steady state detection)算法和EWMA(exponentially weighted moving average)滤波进行稳态检测并结合改进的方法实现了稳态检测数据的预处理;文献[13]采用聚类算法实现了电力数据的异常、毛刺以及极大极小值的处理与优化;文 献[14]针对电厂测量数据一般出自冗余测量系统的特点,考虑不同变量的测量精度,根据基于最大似然原理的数据校正模型进行显著性测量误差检测,并通过校正得到合理数据。但这些方法大多只针对电厂静态数据,对动态性较强的数据处理效果不佳;且仅能修正少数显著异常数据,数据中各种复杂因素引起的噪声未能得到很好地处理。
异常值检测是数据预处理的基础,其中发展最成熟的是基于统计的异常值检测技术[15-16]。Pauta准则适用于数量大的数据异常值处理,该方法较简便。基于此的滤波方法是以随机噪声假设为基础,通过计算均方误差设置阈值,有效剔除异常数据,并根据数据在时间上的连续性,对数据进行修复,从而达到滤波效果。但该方法仅对明显的异常数据进行过滤,对剩余大部分噪声过滤效果不佳。对具有非平稳特性数据的降噪而言,一般的中值滤波、滑动平均滤波等方法效果不明显,取而代之的是经验模态分解(EMD)[17-20]、小波分解等方法。传统的EMD方法存在模态混叠的问题,即一个单独的IMF信号中会含有全异的尺度,且相同的尺度会存在于不同的IMF信号中,对于存在状态切换的火电机组数据,传统的EMD方法在去噪的同时会在一定程度上导致信号的损失,使信号只保留基本趋势而损失很多可能很重要的细节信号,存在噪声剔除不净且不能很好跟踪数据趋势的缺点。另外,实验表明传统EMD方法容易受信号中的异常值影响,将异常值引入固有模态函数,从而使EMD重构后的信号明显偏离原信号。
因此,本文以Pauta准则和EMD方法为基础,充分结合火电机组运行监测数据的特点提出一种改进的状态识别滤波算法,即SREMD算法。该算法在拉伊达准则滤波的基础上,通过识别机组的运行状态,将数据分为稳态过程数据和过渡过程数据,并运用EMD法进行针对性处理。在充分结合电厂数据特点的同时发挥EMD法处理非平稳数据的优势,对火电机组数据进行去噪等处理。
1 改进状态识别滤波算法
1.1 基本思想
在进行EMD分解前先对原始数据进行异常值剔除来消除显著异常值对EMD重构的影响,即需先进行Pauta准则滤波。图1为火电厂给水温度与发电功率原始数据。由图1可知,火电机组数据存在动态性较强的特点,且火电机组为一个状态切换系统,即机组运行状态可以根据整体变化率分为稳态运行过程和状态切换过渡过程2种状态。

图1 给水温度与发电机功率原始数据
因此,本文提出一种稳定状态识别算法,其基本思想是通过调节窗口宽度,根据数据的连续变化率识别出过渡过程和稳态过程。对此计算如下:

式中:Δx为相邻两数据的变化率;Δmax为最大变化率;Δmax为最小变化率;为设定窗口宽度,其最优值通过最小化复合评价指标来确定;12为阈值参数。
长度的窗口内,相邻两数据变化率的均值若大于窗口内最大变化率与阈值参数1的乘积,则可判断此段为上升过渡过程;同样相邻两数据变化率的均值小于窗口内最小变化率与阈值参数2的乘积,则此时处于数值下降过渡过程。否则,判定为平稳阶段,即为稳态过程。
状态识别后,针对稳态过程中信号整体趋于平稳,但存在高频噪声的特点,进行局部EMD分解,并进一步设计重构尺度对稳态过程数据进行重构。同时对原数据直接进行EMD滤波。之后,取直接EMD滤波的过渡过程的数据与重构后的稳态过程段数据进行平滑对接,从而实现2种过程识别并进行针对性处理。
1.2 算法流程
采用SREMD算法对火电机组运行数据进行滤波处理时,首先导入机组运行数据,采用Pauta准则滤波,清除显著异常值数据;然后根据式(1)识别出稳态数据和过渡过程数据;对稳态数据使用EMD方法进行针对性分解和重构,清除噪声数据;同时对过渡数据进行直接EMD滤波;最后将稳态数据与过渡过程数据重新组合并平滑化,完成数据的整体滤波。其算法流程如图2所示。
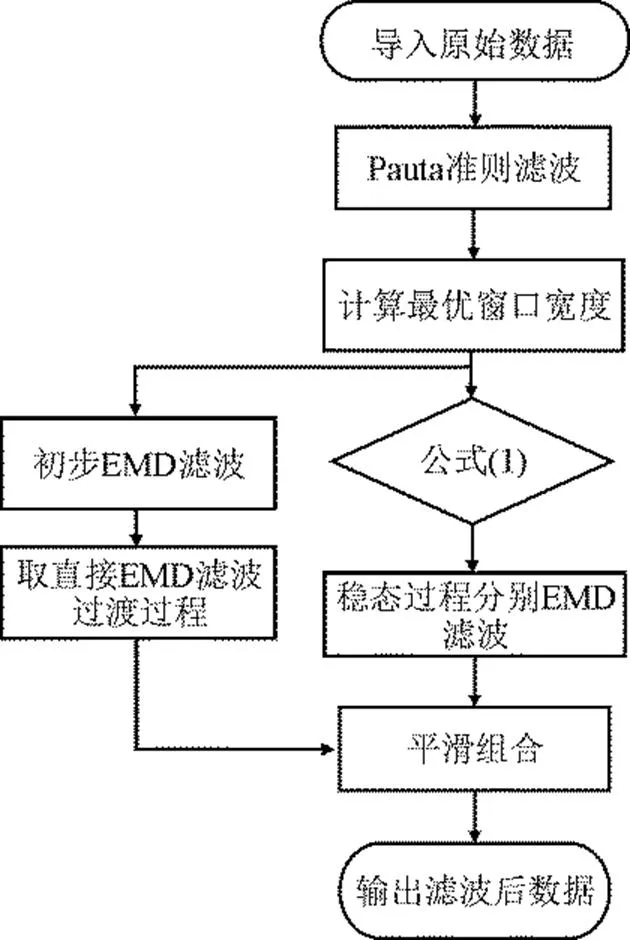
图2 SREMD算法流程
1.3 性能评价指标
通过不同的性能指标[21]来评价SREMD算法的去噪性能。常用的性能指标包括:1)均方根误差RMSE,可以体现信号的整体偏差信息;2)信噪比SNR,体现噪声信息对整体信号的影响;3)平滑度,体现信号的局部变异信息,即是否有较多的局部突变。各性能指标计算公式如下。
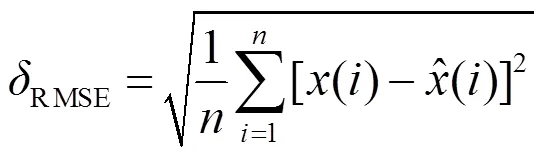
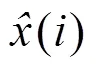
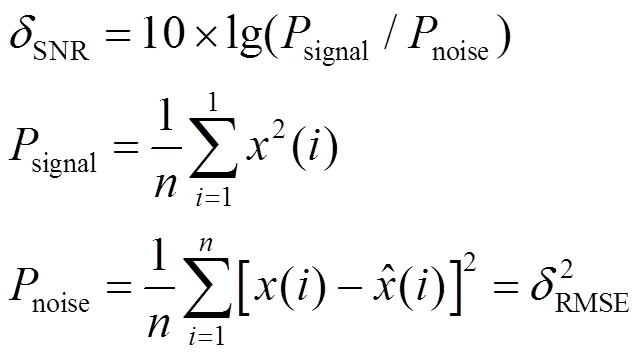
式中signal和noise分别表示信号和噪声的能量。

一般而言,当数据真值已知时,均方根误差越小越好,信噪比越大越好,平滑度越小越好。由于火电机组在线运行的真实数据未知,测量数据本身带有大量噪声,故单独的指标无法直接通过与真实信号的比较来反映去噪效果。
经过分析发现,均方根误差和信噪比都是反映信号细节信息的指标,而平滑度则反映信号的整体趋势特征,且均方根误差与平滑度和信噪比之间呈负相关。因此,本文从数据整体的角度考虑,通过构造复合性能评价指标对算法进行综合性的定量评价,具体计算为
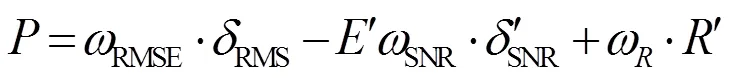
根据复合指标可以计算SREMD算法的最优窗口宽度为
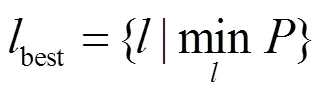
为了更加合理地确定复合指标中各指标的权值,本文通过指标的变异系数定权方法[22]来确定各指标权值。变异系数也称为标准差率,是标准差与均值的比值,能反映指标数值的变异程度,变异系数越大的指标越难实现,因此权值越大。

式中,CVRMSE表示均方误差的变异系数,RMSE、RMSE分别表示指标的标准差和均值。
则

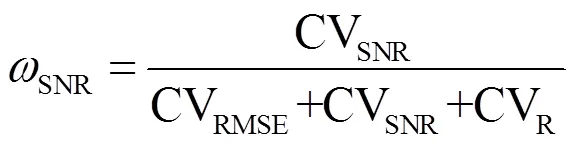
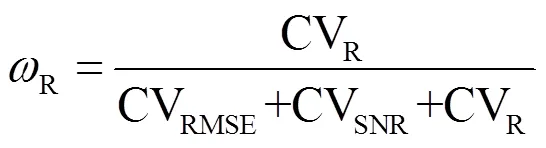
2 实例分析
以某火电机组发电机功率24 h的实测数据为基础进行实验仿真,并从直观效果和量化性能指标2个方面对算法效果进行比较分析。对Pauta准则滤波、EMD法与本文SREMD算法对数据的预处理效果进行验证分析。
2.1 3种算法去噪声效果定性比较
对于火电厂大数据而言,Pauta准则滤波能较好地剔除的异常值,EMD法对高频数据有较好地消除噪声的效果,但在处理火电机组数据时存在明显的局限性,因此本文提出的改进的火电机组数据SREMD算法是很有必要的。
图3为基于Pauta准则的数据滤波。由图3可见,原始数据中存在明显的毛刺,如图3中的3处圆圈标记处,这些数据不满足Pauta准则的条件,能够予以剔除。而对于幅值较小的其他随机噪声,滤波效果欠佳。
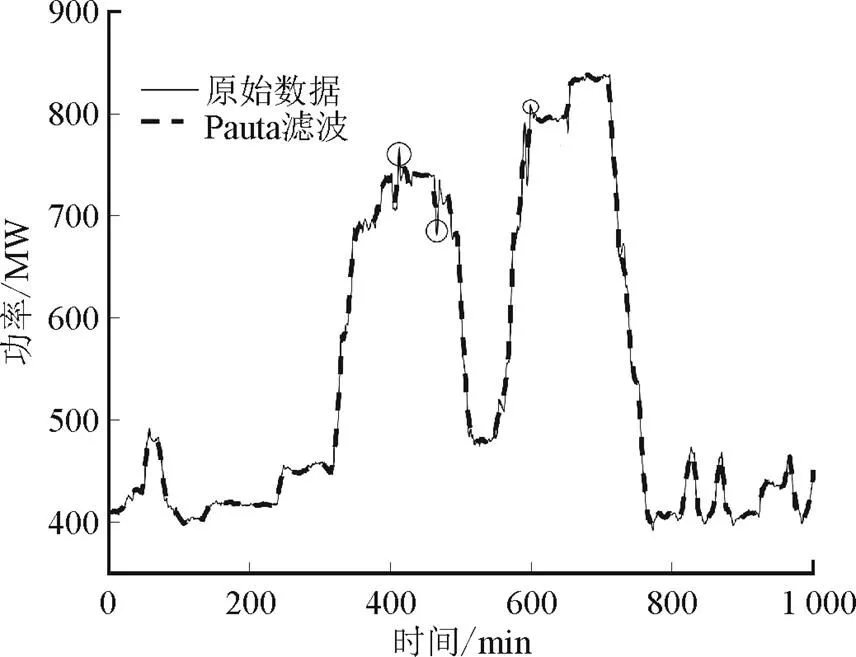
图3 基于Pauta准则的数据滤波
图4为不同重构尺度的EMD滤波。由图4可见,不同重构尺度下EMD滤波效果不同。重构系数过小时滤波效果不佳,过大又会导致重构后的数据波形在很多细节处严重失真。
对比图4中不同重构系数发现:=4时噪声去除效果不佳;=6时会导致原始数据信息损失,不能较好地反映原始数据信号的趋势;5时滤波效果最佳。因此,选取=5时的EMD滤波。此时对火电机组发电机功率数据的噪声滤除效果较好,但依然不能很好地跟踪数据的变化趋势。所以本文结合2种方法,在应用Pauta准则去除显著异常值后再在状态识别的基础上针对性应用EMD滤波。
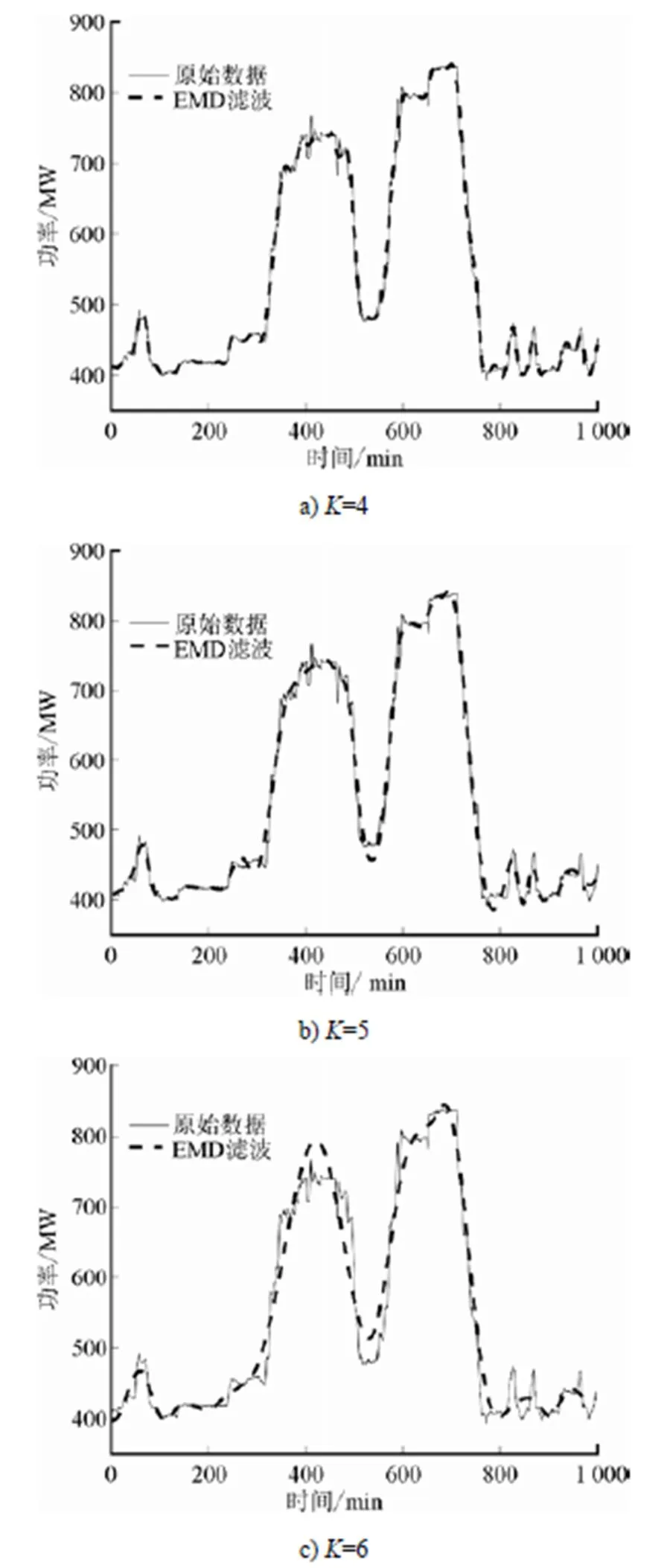
图4 不同重构尺度的EMD滤波
根据式(2)—式(5),计算不同窗口宽度下SREMD算法去噪声复合性能指标,通过寻找复合指标的最小值来确定最优的窗口宽度。由表1可知,当SREMD算法的窗口宽度=19时,复合指标值最小,即算法的综合去噪声性能达到最优。因此,选取窗口宽度=19作为SREMD算法的参数。
表1 不同窗口宽度的复合指标

Tab.1 The composite indexes with different window widths
图5为发电机功率的相对稳态过程识别。图6为基于状态识别的SREMD滤波。SREMD算法是先对原始数据进行Pauta滤波,剔除明显噪声,然后结合整体EMD滤波与稳态过程局部EMD滤波,既很好地剔除了高频噪声,又很好地反映数据整体趋势,效果突出,特别是对于稳态区域,在保证数据整体趋势的情况下,对于高频噪声的处理效果显著。且与传统EMD法相比而言,SREMD法在分解重构前进行了Pauta滤波,消除了异常值对分解重构的影响,避免了直接使用EMD法时出现的固有模态函数受异常值影响从而导致数据重构后偏离原始信号的问题。
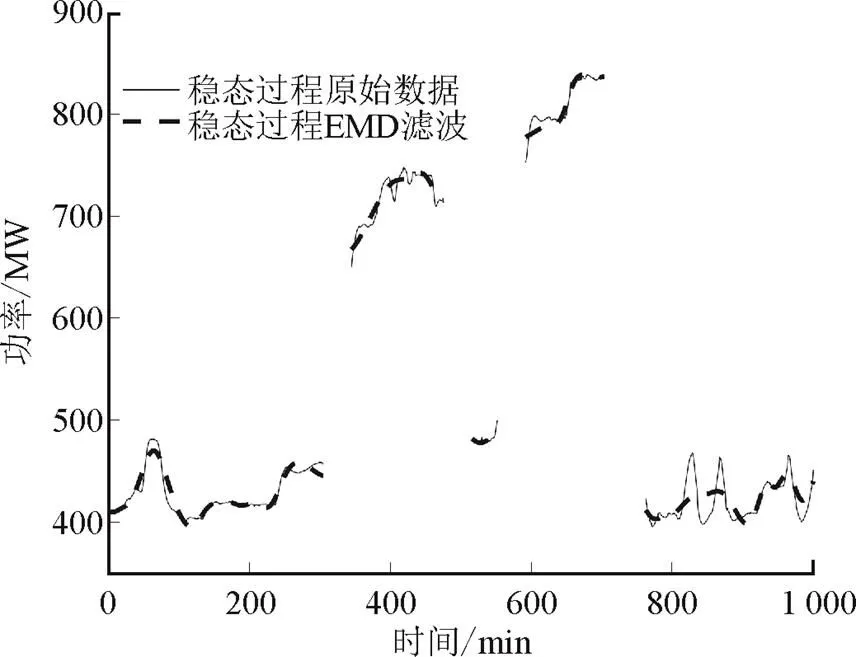
图5 稳态过程识别与滤波
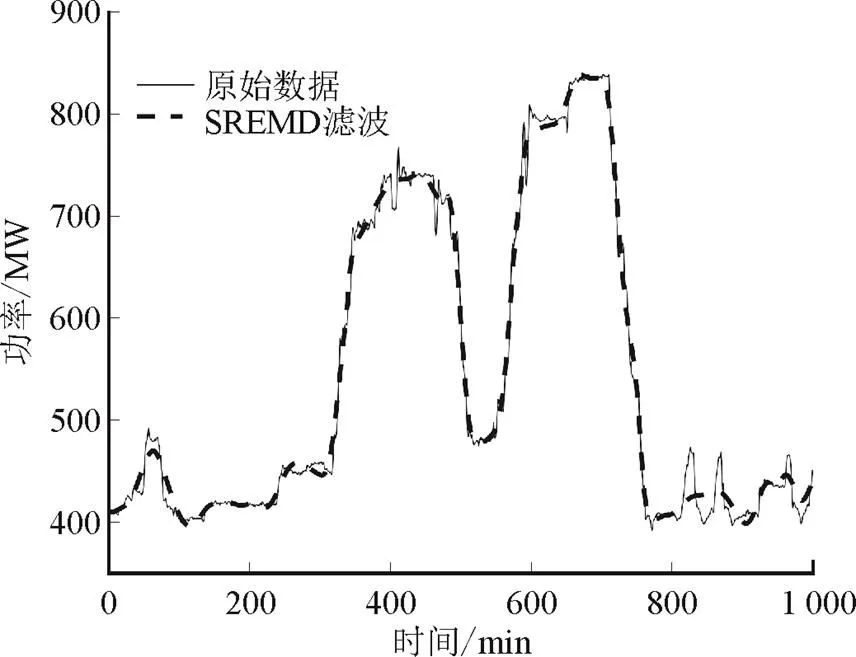
图6 基于状态识别的SREMD滤波
2.2 性能指标定量分析
表2为3种算法的归一化均方根误差、信噪比、平滑度与复合性能指标对比结果。根据表2的数据,就单项指标而言,Pauta滤波的均方误差最小而信噪比最高,这是因为仅去除了显著异常的噪声,与原始数据差异很小。EMD滤波的平滑度指标最好,是因为其直接去除了高频部分的所有本征母函数,剩余部分就是频率较低的成分,但是这样处理会导致很多信息丢失。SREMD滤波的3项单性能指标均较好,其中基于状态识别的SREMD滤波算法复合指标最佳,即其综合去噪声能力最强。
表2 3种算法性能指标比较

Tab.2 The performance index comparison between three algorithms
3 结 论
本文将EMD法与Pauta准则相结合,针对火电机组运行监测数据的特性,提出了一种基于状态识别的SREMD滤波算法。该算法首先采用Pauta准则修复数据中的显著异常值,去除异常数据对本征模函数的影响,通过对数据进行机组运行状态识别,并运用EMD方法对平稳状态数据进行针对性分解重构去除高频噪声,将平稳状态滤波数据与直接EMD滤波得到的过渡过程数据平滑对接,从而在保证信号趋势的前提下较好地去除噪声。
本文最后设计了基于变异指数的加权复合评价指标,根据指标确定SREMD算法的最优窗口宽度,并采用实际数据进行验证SREMD算法的有效性。结果表明,该算法能够更有效对带有状态切换的火电机组数据进行去噪,并能够很好的保持机组数据整体趋势。
[1] 杨世铭, 陶文铨. 传热学[J]. 4版. 北京: 高等教育出版社, 2006: 37-45.
YANG Shiming, TAO Wenquan. Heat transfer[M]. 4th ed. Beijing: Higher Education Press, 2006: 37-45.
[2] 陈雪. 热工测量数据预处理方法研究[D]. 北京: 华北电力大学, 2014: 6-9.
CHEN Xue. Research on data preprocessing method for thermal parameters[D]. Beijing: North China Electric Power University, 2014: 6-9.
[3] FAMILI A, SHEN W M, RICHARD W, et al. Data preprocessing and intelligent data analysis[J]. Intelligent Data Analysis, 1997, 1(1): 3-23.
[4] WANG C L, ZHANG C L, ZHANG P T. Denoising algorithm based on wavelet adaptive threshold[J]. Physics Procedia, 2012, 24(1): 678-685.
[5] 朱龙霞, 肖明美, 栗涛, 等. 基于时间序列分析的火电机组运行优化研究[J]. 河北工业科技, 2017(2): 127-131.
ZHU Longxia, XIAO Mingmei, LI Tao, et al. Research of operation optimization of thermal power unit based on time series analysis[J]. Hebei Industrial Technology, 2017(2): 127-131.
[6] 刘丽平, 叶春, 忻建华. 电厂在线性能分析及故障诊断系统[J]. 热力发电, 2003, 32(11): 76-77.
LIU Liping, YE Chun, XIN Jianhua. Power plant on-line performance analysis and fault diagnosis system[J]. Thermal Power Generation, 2003, 32(11): 76-77.
[7] 马海林, 孙秋红, 徐欣航. 基于数据挖掘技术的电厂运行参数目标值优化[J]. 河北工业科技, 2012(5): 303-307.
MA Hailin, SUN Qiuhong, XU Xinhang. Study on optimization of power plant running parameters based on data minning[J]. Hebei Industrial Technology, 2012(5): 303-307.
[8] 李辉, 陈教超, 司风琪, 等. 数据预处理技术在电厂运行优化系统中的应用研究[J].华东电力, 2007(11): 110-113.
LI Hui, CHEN Jiaochao, SI Fengqi, et al. Application of data preprocessing techonlogy to power plant perfor- mance optimization systems[J]. East China Electric Power, 2007(11): 110-113.
[9] 王一蓉, 王瑞杰, 陈文刚, 等. 基于遗传优化的调控系统缺失数据填补算法[J].电力系统保护与控制, 2016, 44(21): 182-186.
WANG Yirong, WANG Ruijie, CHEN Wengang, et al. A missing data filling algorithm for dispatching and control system based on genetic optimization[J]. Power System Protection and Control, 2016, 44(21): 182-186.
[10] 史林军, 周佳佳, 温荣超, 等. 基于经验模态分解与小波分析相结合的风电功率平滑控制[J]. 电力系统保护与控制, 2016, 44(24): 9-16.
SHI Linjun, ZHOU Jiajia, WEN Rongchao, et al. Power smoothing control of wind power based on combination of empirical mode decomposition and wavelet analysis[J]. Power System Protection and Control, 2016, 44(24): 9-16.
[11] 杨大勇, 葛琪, 董永超, 等. 基于K均值聚类的光伏电站运行状态模式识别研究[J]. 电力系统保护与控制, 2016, 44(14): 25-30.
YANG Dayong, GE Qi, DONG Yongchao, et al. Research on operation state pattern recognition of PV station based on the principle of K-means clustering[J]. Power System Protection and Control, 2016, 44(14): 25-30.
[12] 杨雯宇. 基于稳态检测的电厂数据预处理研究[D]. 北京: 华北电力大学, 2017: 6-26.
YANG Wenyu. Analysis on power plant data preprocessing based on steady state detection[D]. Beijing: North China Electric Power University, 2017: 6-26.
[13] 苏舟, 李灿, 姚李孝, 等. 电力负荷数据预处理研究及应用[J]. 电网与清洁能源, 2017, 33(5): 40-43.
SU Zhou, LI Can, YAO Lixiao, et al. Research and application of pretreatment of electrical load data[J]. Power System and Clean Energy, 2017, 33(5): 40-43.
[14] 刘福国, 王学同, 苏相河, 等. 基于系统测量冗余的电厂异常运行数据检测与校正[J]. 中国电机工程学报, 2003(7): 204-207.
LIU Fuguo, WANG Xuetong, SU Xianghe, et al. Detection and correction on the abnormal operation data based on measurement in a power plant[J]. Proceedings of the CSEE, 2003(7): 204-207.
[15] GUMBELL E J. Statistics of extremes[J]. Applied Ocean Research, 1958, 43(1): 1-30.
[16] ZHAO J, ZHANG G, LA SCALA M, et al. Multistage phasor-aided bad data detection and identification[C]. IEEE Power & Energy Society General Meeting, 2015 (GHTCE).
[17] HUANG N E.Review of empirical mode decomposition analysis[J]. Proceedings of SPIE, 2001(4391): 71-79.
[18] REHMAN N, MANDIC D P. Multivariate empirical mode decomposition[J]. Proceedings Mathematical Physical & Engineering Sciences, 2010, 466(2117): 1291-1302.
[19] HUANG N E, SHEN Z, LONG S R, et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J]. Proceedings Mathematical Physical & Engineering Sciences, 1998, 454(1971): 903-995.
[20] 刘霞, 黄阳, 黄敬, 等. 基于经验模态分解(EMD)的小波熵阈值地震信号去噪[J]. 吉林大学学报(地球科学版), 2016, 46(1): 262-269.
LIU Xia, HUANG Yang, HUANG Jing, et al. Wavelet entropy threshold seismic signal denoising based on empirical mode decomposition (EMD)[J]. Journal of Jilin University (Earth Science Edition), 2016, 46(1): 262-269.
[21] 陶珂, 朱建军. 多指标融合的小波去噪最佳分解尺度选择方法[J]. 测绘学报, 2012, 41(5): 749-755.
TAO Ke, ZHU Jianjun. A hybrid indicator for deter- mining the best decomposition scale of wavelet denoising[J]. Chinese Journal of Chemical Engineering, 2012, 41(5): 749-755.
[22] VOLKER D. Rhythm and speech rate: a variation coefficient for Δe[J]. Language and Language-Processing, 2006(1): 231-241.
Operating data preprocessing using EMD method with state recognition for thermal power plants
ZHAO Yue, FANG Yanjun, DONG Zhengcheng
(School of Power and Mechanical Engineering, Wuhan University, Wuhan 430072, China)
The data from the operating thermal power units are very large and contains complex noise, which is hard to eliminate the noise thoroughly. To solve this problem, an improved empirical mode decomposition filtering algorithm based on the state recognition (SREMD) was proposed. On the basis of empirical mode decomposition (EMD), this SREMD algorithm firstly eliminates the significantly abnormal data by using a filtering method which is based on the Pauta criterion. Then, it recognizes the running states of the unit according to continuous change rate of the data. Finally, it performs corresponding EMD denoising according to the steady state and transition process of unit operation, to adapt to the state switching characteristics. Moreover, this algorithm was applied for actual unit operation data. The results show that, the proposed SREMD algorithm effectively completed the pre-processing of the monitoring data of thermal power units and achieved a better denoising effect on the basis of maintaining the overall trend of the signal.
thermal power unit, data preprocessing, denoising, filtering, Pauta criterion, EMD, state recognition
National Natural Science Foundation of China (51707153); China Postdoctoral Science Foundation (2017M612499)
赵悦(1994—),女,硕士研究生,主要研究方向为智能控制理论研究及应用,2017202080058@whu.edu.cn。
TM932
B
10.19666/j.rlfd.201803045
赵悦, 方彦军, 董政呈. 基于状态识别的经验模态分解法火电厂运行数据预处理[J]. 热力发电, 2019, 48(1): 49-54. ZHAO Yue, FANG Yanjun, DONG Zhengcheng. Operating data preprocessing using EMD method with state recognition for thermal power plants[J]. Thermal Power Generation, 2019, 48(1): 49-54.
2018-03-16
国家自然科学基金项目(51707153);中国博士后科学基金(2017M612499)
方彦军(1957—),男,博士,教授,主要研究方向为火电厂热工控制技术,yjfang@whu.edu.cn。
(责任编辑 杜亚勤)

