基于熵权理想点综合评价的发动机状态特征优选

谷广宇， 刘建敏， 乔新勇

(陆军装甲兵学院车辆工程系, 北京 100072)

近年来，随着“视情维修”和故障预测与健康管理(Prognostic and Health Management，PHM)技术的发展，对装甲车辆发动机的状态评估和剩余寿命预测日益受到业界人士的广泛关注[1-2]。发动机性能随使用年限逐渐退化是一个复杂的机械系统退化过程[3]，其中采用单一特征参数预测发动机剩余寿命不可避免地存在片面性[4]。随着状态检测技术的发展，发动机检测信号中能够提取的特征参数不断增多，基于多维特征的发动机状态评估与预测[5-6]成为必然形势。而如何选取有效信息，则是需要解决的关键问题。

目前，提取有效信息的手段有特征提取与特征选择2种[7]，笔者主要讨论发动机状态特征参数的优化选择方法。特征选择是一种数据预处理手段，其利用一系列度量指标选择相关特征并去除冗余特征。1994年，BATTITI[8]提出以Mutual Information特征选择方法评价特征参数与类别标签的互信息量，二者的互信息量越大，该特征越重要；2004年,YU等[9]提出了FCBF(Fast Correlation-Based Filter)方法，使用信息论中的对称不确定性来评价2个特征的相关性，删除冗余特征；2005年,PENG等[10]基于互信息计算提出了经典的mRMR信息论特征选择方法，兼顾了特征与类别之间的相关性和特征之间的冗余度。以上3种广为流行的特征选择方法均是以单一度量指标进行特征选择。张彬[11]结合轴承和航空发动机的性能特点提出了包括相关性、单调性、鲁棒性等一系列性能退化特征的评价指标，但最终的优化选取结果仍依赖主观经验对比分析评价结果。

鉴于此，笔者在对文献[11]中评价指标改进的基础上，从信息量的角度出发，提出一种基于熵权理想点的多指标评价方法，以期给出多种评价指标下对特征参数的客观定量评价方法，以及在该方法评价结果下的发动机寿命预测方法。

1 特征参数的综合评价指标

理想的状态特征参数应具备同类个体普适性、性能退化一致性、失效共趋性及干扰鲁棒性等属性。目前，有关状态特征参数的定量评价指标研究很少，在此主要采用相关性、单调性、离散性及鲁棒性等指标进行状态特征参数的综合评价。

1.1 相关性指标(C)

相关性指标的定义为

(1)

式中：X={x1,x2,…,xN}，为某一特征参数序列；T={t1,t2,…,tN}，为相应时刻的时间序列；N为相应的监测点数。

相关性指标来源于相关系数的概念，通过取绝对值将其限定在[0,1]。相关性指标反映了特征参数序列与监测时间序列之间的线性相关程度，并在一定程度上反映了特征参数在优劣变化中同类个体的普适性。某特征参数的相关性指标值越大，则其与寿命间的线性相关性也越大，说明该特征参数也能更好地描述性能退化。

1.2 单调性指标(M)

单调性指标的定义为

(2)

单调性指标部分刻画了特征参数变化的一致性，其大小取决于单调非减或单调非增趋势的整体强度，其值限定在[0,1]。某特征参数的单调性指标越接近于“1”，则表明随着性能退化的加剧，该特征参数表现出越好的单调性趋势，从而也可越好地进行技术状况评估与剩余寿命预测。

1.3 离散性指标(D)

离散性指标的定义为

(3)

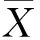
离散性指标是基于群体统计量而定义的，其考虑了特征参数的变化范围和其在检测过程中的分散性，其取值也为[0,1]。某特征参数的变化范围越大且其标准差越大，则这一特征参数的离散性指标越接近于“1”，说明该装备的技术状况等级的可分性越好。

1.4 鲁棒性指标(R)

鲁棒性指标的定义为

(4)

鲁棒性指标是基于特征参数序列波动程度而定义的，其描述了特征参数对外点等干扰的鲁棒性，其取值为[0,1]。某特征参数随使用时间的变化曲线越平滑，则其鲁棒性指标越大，该特征参数变化趋势的不确定性越小，可预测性越强。

2 基于熵权理想点的多指标综合评价方法

在特征参数的评价及优选过程中，由于各指标的地位和权重缺乏统一标准，因此从信息量的角度出发，根据熵权评价指标在特征参数中的作用，并结合理想点法求得特征参数的相似度，得到基于熵权理想点的多指标综合评价方法。

2.1 熵的概念

“熵”是信息论中最重要的基本概念，它表示从一组不确定事务中提供信息量的数量。对于变量序列Z={z1,z2,…,ZK}，其信息熵[12]的定义为

(5)

在决策中，某指标的信息熵越小，说明该指标提供的信息量越大，不同状态特征之间所表现的差异越大，该指标也就越容易区分不同状态特征的优劣。因此，在优选排序中某指标所起作用越大，该指标的权重应越大；反之，则该指标的权重也应越小。

2.2 指标熵权的确定

利用熵确定各评价指标客观权重的主要步骤[13]如下：

1) 建立标准化决策矩阵。为消除各指标因变化范围、数量级不同而对决策结果产生的影响，需对决策矩阵进行标准化处理，得到归一化决策矩阵

根据评价指标的属性，第j个特征的第i个指标zij的标准化参数为

(6)

式中：n为特征参数的数量。

2) 计算第i个指标的输出熵

(7)

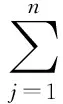
3) 根据输出熵计算第i个指标的熵权

(8)

式中：m为评价指标的数量。

2.3 理想点法

理想点法最初是在改进“妥协解应与理想解距离最近”的概念所发展出来的一种多目标决策方法[14]。其中：理想点是指各指标属性均达到最好时的值；负理想点是指各指标属性均达到最差时的值。该方法通过构造多目标决策问题的理想点和负理想点，并以距离理想点和负理想点的远近来评价各个方案的好坏，得出一个评价结果。基于理想点法的评价过程如下：

1) 根据前文归一化决策矩阵R和各指标熵权Wi，构建加权决策矩阵

2) 计算理想点与负理想点，分别为

3) 计算相似度。若第j(j=1,2,…,n)个特征参数的决策向量Pj=(p1j,p2j,…,pmj),则该特征参数的相似度

(9)

显然，Tj∈[0,1]。相似度Tj越大,说明决策向量Pj越接近理想点。其中：当Tj=1时，Pj为理想决策；当Tj=0时，Pj为负理想决策。因此，可由相似度Tj对各方案进行排序，Tj较大者较优。

3 某型发动机状态特征参数评价优选

发动机技术状况检测参数的确定原则为：能反映发动机的动力性能和经济性能，以评估发动机的技术状况；能反映发动机技术状况变化过程和磨损情况，以评估发动机的使用时间和剩余寿命；在技术上能实现实车不解体检测[15]。在某型发动机的寿命试验期间，提取供油提前角、燃油流量、发动机加速时间、发动机减速时间等9个可检测的特征量作为评估发动机技术状况的具体参数，并对各特征参数以“1”为单位进行规范化预处理，其部分结果如表1所示。

3.1 发动机状态特征参数综合评价

发动机状态特征参数综合评价步骤如下：

1) 根据式(1)-(4)，计算发动机状态特征参数的评价指标，其结果如表2所示。

2) 确定评价指标的客观权重。对归一化矩阵采用改进的输出熵计算方法，得到评价指标输出熵

H={0.989,0.994,0.991,0.995}，

以及评价指标的熵权

W={0.351,0.198,0.282,0.169}。

3) 计算理想点。以熵权W和归一化决策矩阵R构建加权决策矩阵，可计算得到

P+=(0.347,0.210,0.292,0.259)；

P-=(0.028,0.030,0.036,0.106)。

4) 计算各特征参数与理想点的相似度，并按从大到小顺序进行优选排序，结果见表3。

3.2 发动机状态预测特征参数选择

按表3中的优选顺序分别选取2～9个种特征参数，并依据相应的相似度进行加权融合，得到的预测参数如表4所示。

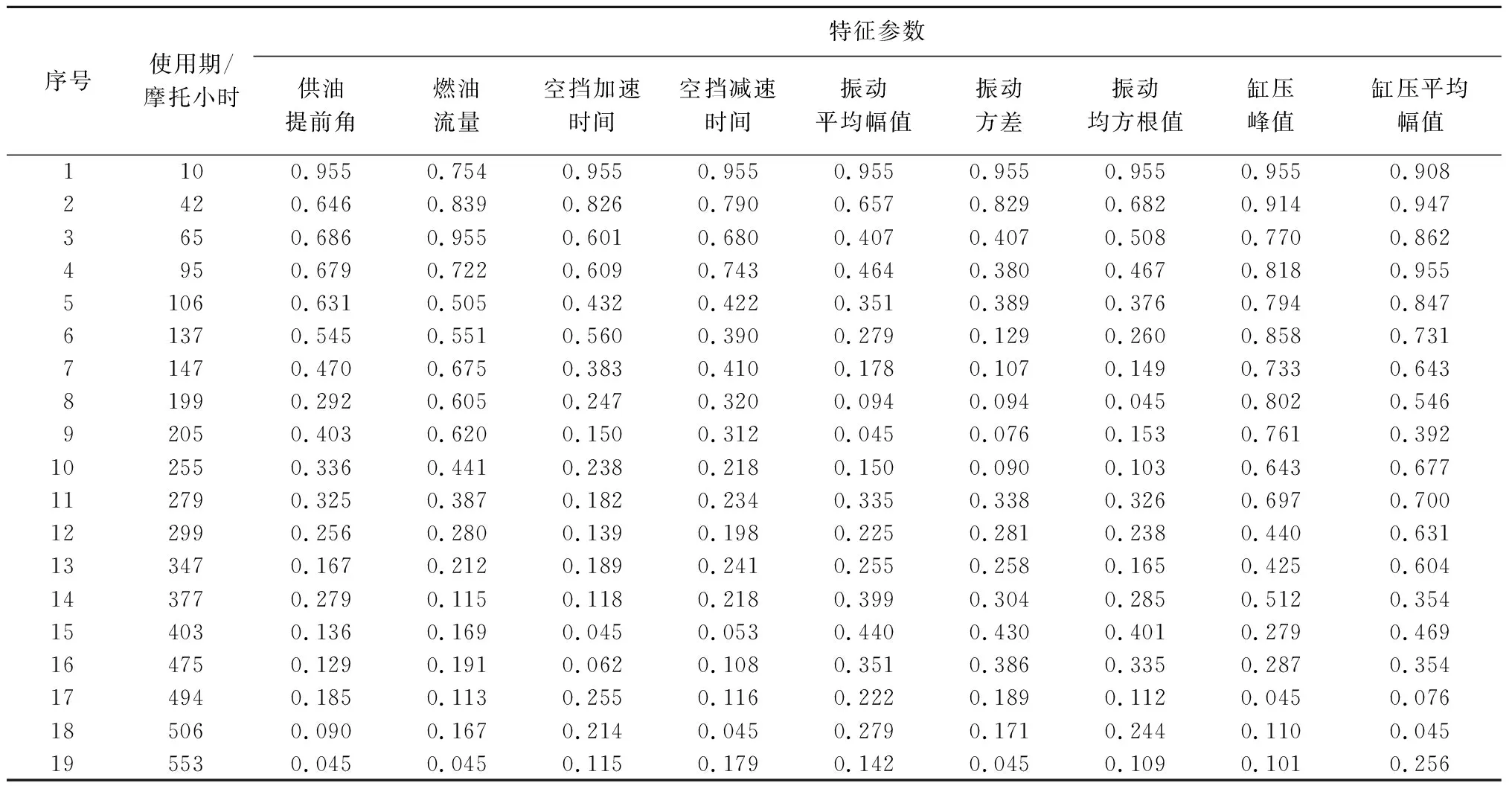
表1 发动机技术状况特征参数

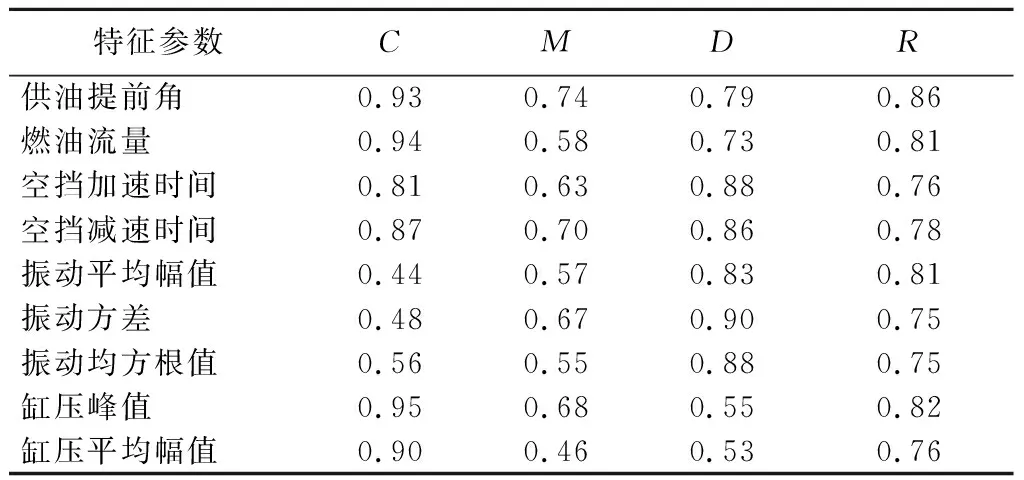
表2 发动机状态特征参数评价指标

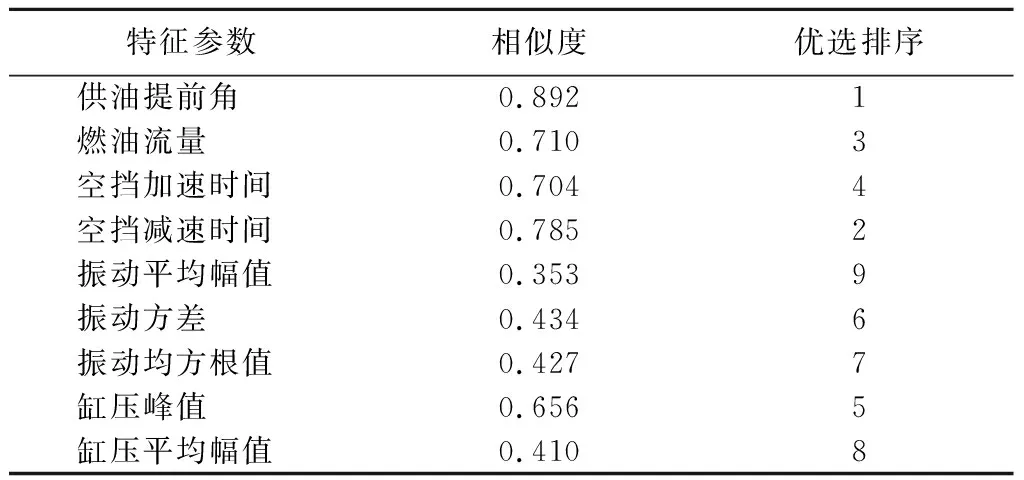
表3 发动机状态特征参数相似度及优选排序

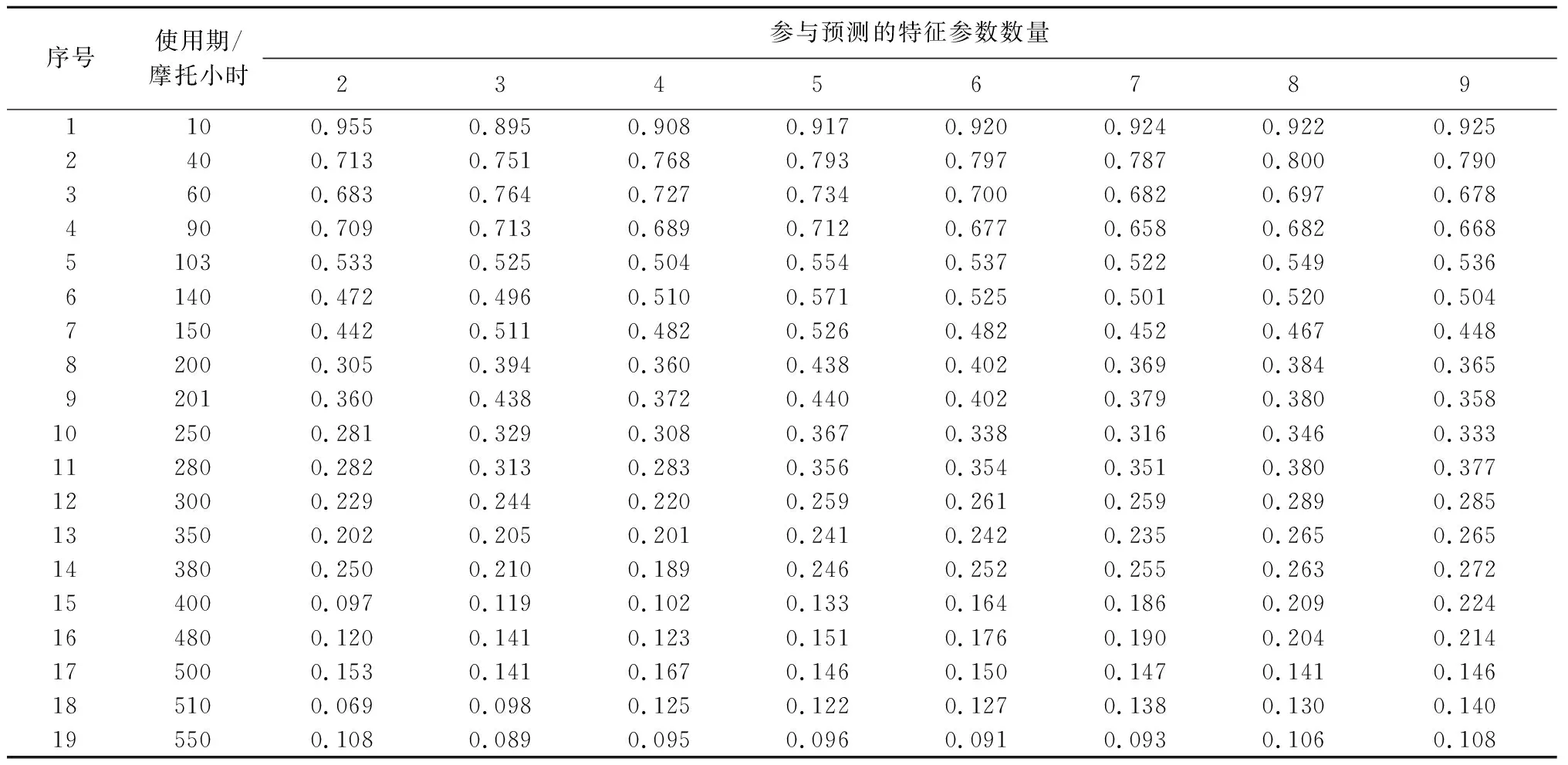
表4 不同数量特征参数加权融合的预测参数

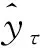
调整RBF神经网络的输入层神经元及分布密度，当平均相对误差达到最小时，结合表4进行预测，其结果如图2所示。可以看出：1)随着评价较高的特征参数依次加入，平均相对误差首先呈现明显下降趋势，之后因评价较低的特征参数带来的冗余和干扰信息的增加而略有上升，符合特征参数优化选择的一般规律；2)当选取5个特征参数预测时，预测的平均相对误差最小，约为3.15%，此时选取的5个特征参数为供油提前角、发动机减速时间、燃油流量、发动机加速时间和缸压峰值。

4 发动机剩余寿命预测

已知该型发动机在550摩托小时进入大修期，选取5台临近大修的发动机，采用Bootstrap小子样统计方法[17]分析其状态特征融合后的预测参数分布，得到其预测参数服从N(0.078 6，0.001 5)正态分布。假设当该型发动机预测参数进入大修期的概率>50%时，判定此发动机需要进厂大修，则预测参数的阈值为0.078 6。

图3为该型发动机300～500摩托小时内的预测参数样本值，及采用RBF神经网络预测模型对500摩托小时以后的参数多步预测后得到的预测值变化曲线。可以看出：该发动机在使用达559摩托小时后，预测参数将低于大修阈值。

继续运行该发动机，当检测到的预测参数低于大修期值时，将其作为样本值与预测值进行对比，如图4所示。可以看出：该发动机实际寿命约为560摩托小时。

使用该方法对技术状况不同的多台发动机从不同使用期开始进行寿命预测，结果如表5所示。可以看出：对使用300摩托小时以上的发动机进行寿命预测时，预测误差<7%，且随着大修期临近，预测误差逐渐减小。

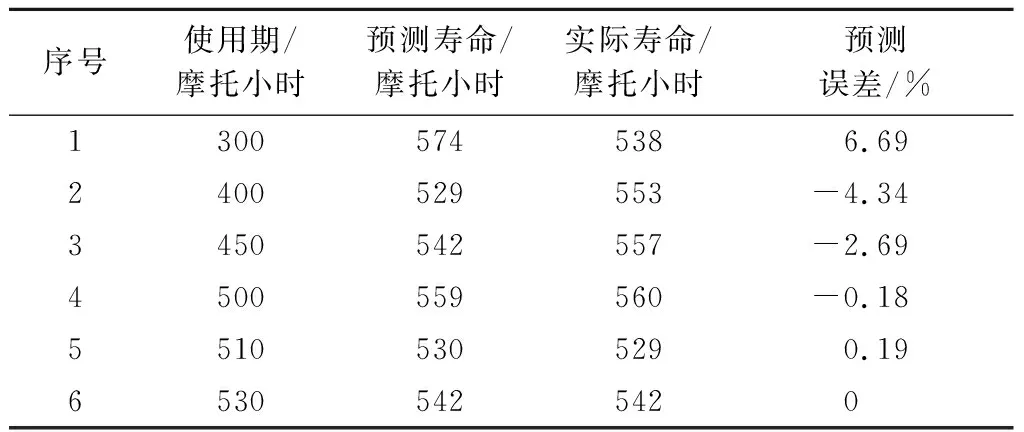
表5 技术状况不同的多台发动机寿命预测

5 结论

为优化发动机状态评估与预测过程中的特征评价及选取方法，建立了特征参数的综合评价指标，提出了一种基于熵权理想点的综合评价方法，并通过实例分析了其应用效果。主要结论如下：

1) 该综合评价方法能够对发动机状态特征参数进行客观有效评价，且能够得出发动机状态特征参数在评估和预测中的优劣排序。

2) 在某型发动机状态预测过程中，根据得出的优选顺序，选取不同数量特征参数进行预测时，发现预测误差随着特征参数增加呈现先下降后上升的趋势，且在选用前5个特征参数预测时的平均相对误差达到最小，约为3.15%。

3) 基于熵权理想点的多指标评价优选结果，可直接通过加权融合的方法应用于发动机状态的多参数预测中，且随着大修期逐渐临近，预测误差将逐渐减小，说明预测结果能够为基于发动机状态的维修决策提供数据支撑。