基于作战任务的备件保障概率分配及其需求量预测模型

薛 辉, 刘广宇, 刘铁林,刘 丽

(1. 陆军工程大学石家庄校区装备指挥与管理系，河北 石家庄 050003； 2. 空军石家庄飞行学院， 河北 石家庄 050071； 3. 陆军步兵学院石家庄校区机械化步兵侦察系， 河北 石家庄 050200)

由于遂行联合火力打击任务的武器装备种类、功能多样，不同作战任务对装备的能力需求不同，所需消耗的备件量也不同，且战时部队携行备件能力有限，因此配置种类合理、数量准确的备件是完成战时装备保障和战场抢修任务的根本保障和先决条件，迫切需要研究不同作战任务背景下备件需求量的配置优化问题。

战时备件需求量是指装备在整个作战过程中(包括作战准备阶段)，在规定时间内能够满足装备维修保障需求的备件数量。装备能否得到快速修复与其设计特性(损坏部位是否容易达到)和计划的保障资源(是否有匹配的备件)有关。目前针对装备设计特性和使用环境造成的技术损坏而产生的备件需求研究较多，但对装备作战中由于受击损坏而产生的备件需求研究相对较少。总体来看，有关备件需求问题研究的方法主要有经验法、解析模型法和计算机仿真法3大类[1]。其中：经验法主要利用相似系统理论和Bayes方法，基于已有相似装备的备件消耗信息预测备件需求量，如相似产品预计法[2-3]、备件保障概率法[4-5]。由于该类方法主要依赖主观经验确定现有装备缺乏的现场信息，且主要针对平时的备件需求进行预测，因此难以保证预测结果的准确性。针对战时备件需求预测问题，虽然传统的经验推算法能够准确、高效地预测具有大量实战经验和数据的战斗案例，但也缺乏科学合理的定量分析。解析模型法是指假设备件寿命分布已知的建模方法，其预测精度取决于拟合出的备件寿命分布情况[6]，备件寿命分布越接近实际，预测结果越准确。如：董骁雄等[7]针对装备部署部队后因使用环境变化造成可靠性下降，导致研制阶段确定的初始备件方案与现实需求差距较大的问题，基于相似系统理论和Bayes方法提出了确定初始备件需求的新方法，但该方法侧重于装备平时的技术损坏，未考虑战时双方对抗过程中由于受击损坏而造成的备件需求；张闯等[8]基于备件的重要度采用主成分分析法确定了备件品种需求，但备件重要度的排序主要依赖主观经验，且未考虑不同作战任务的特点；杨宇航等[9]采用仿真方法研究了备件动态需求变化规律和备件需求量预测问题，但是未对受击损坏模式下备件需求量预测仿真方法进行研究。总之，传统的战时备件需求量预测方法仍然存在以下3方面的问题：1)预测备件需求量主要基于武器装备的可靠性指标，未考虑双方的作战方案及实际对抗情况；2)备件保障概率分配主要依据其设计特性，未考虑作战任务的具体特点和规律；3)未考虑装备修复能力直接影响双方作战损耗情况以及备件需求量。由于战时装备作战任务强度大、火力对抗激烈，其技术损坏率和受击损坏率明显增大，备件需求量预测影响因素多且关系复杂。因此，战时备件需求量预测是一个时敏的、随机的动态过程，应结合作战任务实际和装备保障业务特点开展预测。笔者聚焦军事对抗过程、兼顾受击损坏和技术损坏2种损坏模式，首先，以敌方目标为参考，计算不同作战任务中我方装备综合战斗力指数，并利用层次分析法(Analytic Hierarchy Process，AHP)确定装备作战任务贡献度(简称“装备贡献度”，即装备在包含它的装备体系和给定的作战任务条件下，对装备体系完成作战任务所发挥的能力或作战效果的价值)，依据军事指挥员对装备总体使用可用度的要求动态分配装备保障概率，进而根据零部件对装备功能的重要度分配相应备件的保障概率；然后，根据装备损坏模式预测战时备件需求量，其中技术损坏通过分析零部件的寿命分布规律构建预测模型，实现备件需求量的预测，受击损坏主要在明确不同作战任务火力分配方案[10]的前提下确定装备受击损坏规律，构建预测模型，实现备件需求量的预测，从而有效提高了战时备件需求量的预测精度，为战时备件需求量预测提供新的思路和方法支持。

1 战时备件需求影响因素分析

战时备件需求影响因素多，结合作战实际，笔者主要考虑装备部署数量和使用频度、装备的地理分布和使用环境、装备使用可用度(简称“使用可用度”)、规定的备件保障概率、平均供应时间、修理策略(如换件修复、原件修复等)、保障力量的携运行能力、战斗损伤估计8个方面，其中使用可用度和备件保障概率是2个主要影响因素。

1.1 使用可用度[11]

可用度(availability)是指装备在任一随机时刻需要和开始执行任务时，处于可工作或可使用状态的概率,它是装备可用性的概率度量。装备不可用并非均是由损坏造成的，为了使装备保持完好状态，需要进行预防性维修活动。若同时考虑修复性维修和预防性维修，则不能工作时间包括排除故障维修时间和预防性维修时间，因此可达可用度(achieved availability，Aa)与平均维修间隔时间(Mean Time Between Maintenance，MTBM)、平均修复时间 (Mean Time To Repair,MTTR)、平均预防性维修时间 (Mean Preventive Maintenance Time，MPMT)等指标有关，其计算公式为

(1)

在装备使用过程中，不仅排除故障和预防性维修会造成装备不能工作，还有很多因素，如因等待供应备件而造成装备不能工作，因此使用可用度(operational availability，Ao)除了与平均维修间隔时间(MTBM)、平均修复时间(MTTR)、平均预防性维修时间(MPMT)有关外，还与备件平均供应时间 (Spare Mean Supply Time，SMST)有关，其计算公式为

(2)

在战时，平均供应时间SMST与其他3个指标明显不同的是受战时保障资源的约束和具体交战态势的影响，该备件能否得到保障是不确定性事件。

1.2 备件保障概率

备件保障概率(P)是指在规定的时间内，需要备件时不缺备件的概率，或零部件损坏数不超过备件供应数的概率，亦称备件满足率[12]，它是影响SMST的因素之一。由于战时备件供应受作战环境的影响，因此备件供应平均延误时间 (Spare Mean Delay Time，SMDT)与战时备件平均供应时间之间的关系为

SMST=(1-P)SMDT，

(3)

战时装备使用可用度

(4)

则由式(4)可知备件保障概率

(5)

陶小创等[4]将备件保障概率(P)定义为组成装备的所有LRU(Line Replaceable Unit)备件满足装备需求的概率。备件保障概率存在于装备功能组成分解结构的不同层次，如系统级、分系统级和LRU级。因此，装备系统的备件保障概率可按照装备功能组成分解结构自上而下分配至LRU级别。

1.3 其他因素

备件需求量预测除了以上2个主要影响因素外，也与装备的技术损坏率和受击损坏率密切相关，文中作为已知量给出。对于装备携运行量，文献[13-16]作者在优化建模时将备件体积、费用、质量等作为约束条件，为简化模型，笔者暂不考虑。

2 战时备件保障概率分配模型构建

2.1 问题假设

1) 假设已知对抗双方的火力打击方案[10]；

2) 装备在非火力对抗阶段仅考虑任务强度造成的自然退化并服从指数分布，且主要集中在作战准备阶段；

3) 装备在火力对抗阶段仅考虑受击损坏情况并服从伯努利分布，且主要集中在火力对抗阶段；

4) 不同装备的保障概率分配与其对完成作战任务的贡献度有关；

5) 不同任务中装备的贡献度不同；

6) 不考虑损坏零部件的维修和更换时间；

7) 不考虑携行备件受敌方打击造成的损失，且备件不发生自然退化、失效等；

8) 保障部门的携行能力有限，影响备件携行量的因素很多，笔者仅考虑携行备件量；

9) 不考虑保障设备故障对装备保障效能产生的影响，保障设备的可靠性、维修性参数值为理想值。

2.2 装备综合战斗力指数评估模型[17]

战时装备由于受战场恶劣环境的影响和各种保障资源的制约，难以满足所有装备既定的保障概率，实施保障时需要优先考虑满足对完成作战任务贡献度高的装备保障需求。笔者依据装备战斗力指数及其与敌方目标对抗的损失交换比(简称“对抗损失交换比”)，建立不同作战任务下装备综合战斗力指数评估模型，利用不同装备综合战斗力指数比值构建AHP法的判断矩阵，确定不同作战任务中装备的贡献度，以装备贡献度为依据分配装备保障概率。

假设1：我方有M种装备，敌方有N种装备，我方第m(m=1,2，…，M)种装备对敌方第n(n=1,2，…，N)种装备的最大损失交换比(也称为作战效能平衡点)为Km∶Kn，即当我方用Km个第m种装备与敌方的Kn个第n种装备进行作战时，交战结果为平手，其极限情况为1∶0或0∶1，为此，可设Km+Kn=1。

假设2：PHm和PLn为双方2种装备直接交战的标准战斗力指数。由于PHm或PLn能否得以发挥与对方是否投入了该种交战装备有关(即与作战目标有关)，因此，2种装备的直接交战标准战斗力是否存在与双方装备投入和作战运用方案有关。

根据战斗力指数最大发挥原则，第n种装备对所有存在交换比不等于0的装备综合战斗力指数均为PLn，则第m种装备对第n种装备的战斗力指数为PLn(Km/Kn)；反之，若以第m种装备为参照，则双方的综合战斗力指数分别为PHm和PHm(Kn/Km)。由于在实际作战中双方均有多种装备参与，因此，笔者根据战斗力指数最大发挥原则，选取较大的综合战斗力指数值作为参照依据，来计算第m种装备的综合战斗力指数，即PHm=max(PHm，PLn(Km/Kn))，则我方M种装备更新后的综合战斗力指数为PH=(P1,P2,…,PM)=(PHm)1×M。

2.3 备件保障概率分配模型

笔者针对作战任务，分装备层和零部件层2个层次进行备件保障概率分配。

1) 在装备层，主要根据装备在不同作战任务中的综合战斗力指数，利用AHP法确定装备贡献度。在军事指挥员给定装备体系使用可用度要求的基础上，根据装备贡献度的高低分配其整体保障概率。

将我方更新后的战斗力指数PH=(P1，P2，…，PM)进行两两比较，并选择比值与标度1～9或其倒数最为接近的数值构建判断矩阵，求解判断矩阵的最大特征根及其对应的特征向量，对特征向量进行归一化处理可得权重向量θH=(θ1，θ2，…，θM),即我方装备的贡献度向量。对判断矩阵进行一致性检验，若通过一致性检验，则认为判断矩阵是满意的，装备贡献度是合理的。

设该次作战任务中军事指导员要求的所有装备的总体使用可用度为Ao，则我方第m种装备的使用可用度

(6)

再结合已通过经验数据统计获得的该装备的平均维修间隔时间(MTBM)、平均修复时间(MTTR)、平均预防性维修时间(MPMT)以及备件供应平均延误时间(SMDT)等参数，根据式(5)可求得该装备的整体保障概率(Pm)。

2) 在零部件层，主要根据装备零部件对装备整体功能的重要度分配相应备件的保障概率。文献[4,10]作者根据用户和装备研制要求中的可达可用度指标，采用Delphi法对装备分系统和LRU备件保障概率进行了分配，该方法主要依赖专家经验进行分配。笔者参考可靠性分配准则和方法，根据零部件对装备的重要度分配其相应备件的保障概率，对于重要度高的零部件,应分配较高的保障概率。装备可按照分系统级、设备级、零部件级逐级展开，是由分系统、设备、零部件通过串联、并联、混联等方式组成的，各组成部分发生的故障不一定能引起装备的故障。设ωl为零部件故障对装备故障的影响，即零部件l(l=1,2,…,L)的重要度，则

(7)

我方第m种装备第l个零部件的备件保障概率为

(8)

3 战时备件需求量预测模型

笔者考虑技术损坏和受击损坏2种损坏模式，建立战时备件需求量预测模型。

3.1 技术损坏备件需求量预测模型

参考GJB4355—2002[12]及文献[18]，零部件寿命分布形式主要有指数分布、威布尔分布和正态分布3种。

3.1.1 指数分布

已知第i个零部件在装备中的单机安装数为Ni，累积工作时间为ti，故障率为λi，备件保障概率为Pi，则该类零部件的备件需求量si与其保障概率pi之间的关系为

(9)

式中：当q从0开始逐一递增至si，使pi≥规定的保障概率时，对应的si值即为所求的备件需求量。

当Niλiti>5时，可采用正态分布近似计算备件需求量，其简化计算公式为

(10)

式中：μi可从正态分布分位数表中查得，如表1所示。

表1 常用的正态分布分位数表

3.1.2 威布尔分布

已知第j个零部件的单机安装数为Nj，平均供应时间为tj，尺度参数为αj,形状参数为βj(j=1,2,…,J)，位置参数为0，则该类零部件的备件需求量sj与其保障概率pj之间的关系为

(11)

式中：

(12)

备件需求量

(13)

3.1.3 正态分布

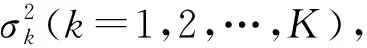
(14)

备件需求量

(15)

式中：μk的算法与μi相同;E为平均寿命。

3.2 受击损坏备件需求量预测

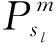
(16)

第m种装备第l个零部件的备件需求量sl可由

(17)

4 案例想定与结果分析

4.1 参数假设

为验证模型的可行性及合理性，假设在实际作战中可通过侦察手段、敌情预判、战场态势分析等方法获得各项参数。军事指挥员要求所有作战装备的整体使用可用度Ao=0.8时，才能定下作战决心。我方装备的技术损坏均服从指数分布且主要集中在作战准备阶段，受击损坏服从伯努利分布且主要集中在火力对抗阶段。我方装备种类、数量、损坏率及工作时间等相关数据如表2所示。

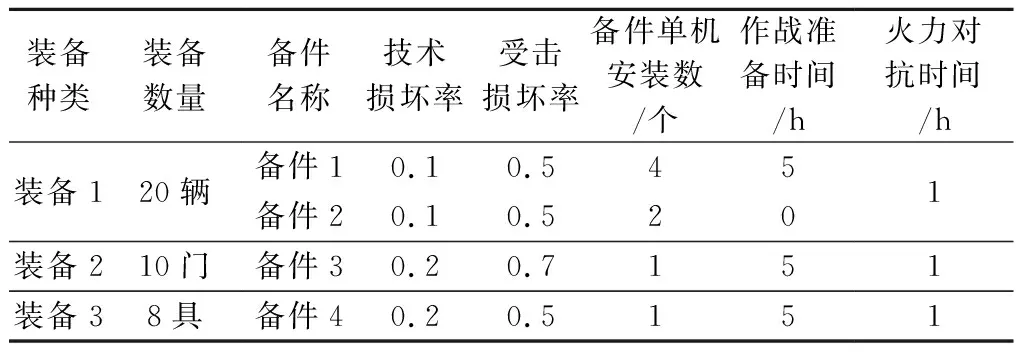
表2 我方装备种类、数量、损坏率及工作时间等相关数据

我方装备与敌方目标的标准战斗力指数及对抗损失交换比如表3所示。

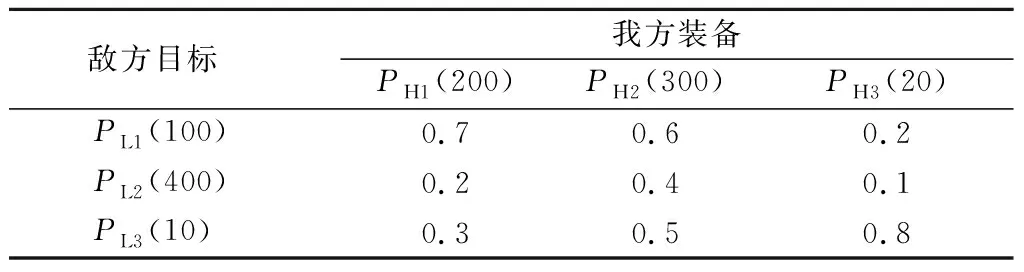
表3 我方装备与敌方目标的标准战斗力指数及 对抗损失交换比

我方装备的各项可靠性、维修性参数如表4所示。

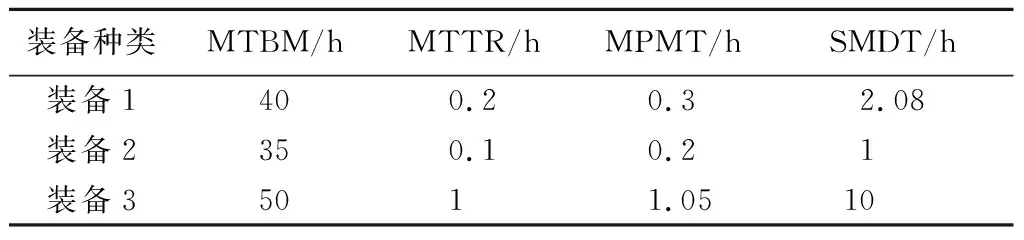
表4 我方装备的可靠性、维修性参数

4.2 备件需求量预测结果

以PH1为例，根据PH1与敌方目标PL1、PL2、PL3的损失交换比以及敌方目标的标准战斗力指数，可得PH1可选取的综合战斗力指数分别为100×0.7/0.3=233.33，400×0.2/0.8=100，10×0.3/0.7=4.29。选取最大值233.33与自身标准战斗力指数200进行对比，按照战斗力指数最大发挥原则，最终选取233.33作为该作战任务背景下装备PH1的综合战斗力指数。同理，可得PH2、PH3的综合战斗力指数分别为300、44.44。

对比三者的综合战斗力指数值，选取与数字1～9或其倒数最为接近的数值构建判断矩阵,可得

(18)

其最大特征根为3.014 2，对其特征向量进行归一化处理可得权重向量θH=(0.166 6，0.093 8，0.739 6)，即我方各装备的贡献度，由式(6)可得我方装备1、2、3的使用可用度分别为0.982 6、0.990 2、0.925 0。

由式(5)可得我方装备1、2、3的整体保障概率分别为0.9、0.95、0.8。为简化计算，假设各装备的零部件重要度均为1，则可根据任务阶段划分，分别求取不同作战任务阶段的备件需求量。由于备件需求量为整数且不小于保障概率，则根据式(10)、(17)可得我方各装备的备件需求量，如表5所示。

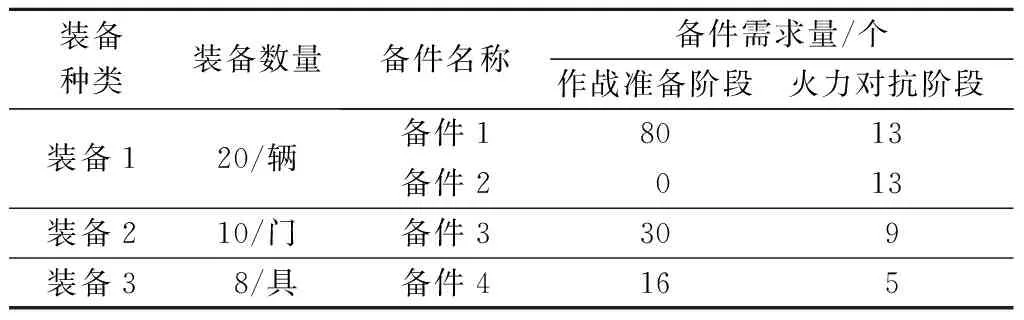
表5 我方各装备的备件需求量