探究一元微积分中几大定义及应用
(大连财经学院基础教育学院 辽宁 大连 116600)
数学中的定义是人类智慧的结晶,是对实际问题的一种精确表达,它来源于实际问题并应用到实际生活当中,它讲究严密性,完美性。正确理解并灵活运用数学中的每一个定义,是掌握数学基础知识和运算技巧、也是学好数学这门学科的重要前提。极限、连续、导数与定积分是一元微分学中最基础也是最重要的研究内容,掌握好它们的定义及定义的应用至关重要,下面主要以它们为研究对象,探讨一下它们的定义及其应用实例。
1.极限定义及其应用
极限是微分学中非常重要的概念之一,它包括数列极限和函数极限,其中函数极限是高等数学教学的重点研究对象,它贯穿微积分教学的始终,因该说微积分中几乎所有重要概念都是通过极限来定义的,如连续,导数,定积分,重积分,级数的敛散性等等的定义都与极限有关,因此学好极限对学好微积分是至关重要的,这也就要求我们无论是对极限的定义还是求解方法都要熟练掌握,从而为学好微积分的打下良好的理论基础.首先我们先回顾一下数列极限的定义及其应用。
1.1 数列极限
定义:设数列{an},若对任意的ε>0,存在正整数N以及常数A,使当 n>N时,恒有,则称{an}的极限为 A(n→∞),记为。
数列极限定义是学习极限理论时第一个接触的概念,这种数学语言的定量定性定义,对于初学者来讲很难理解,在教学中,为了达到更好的教学效果,在讲解极限定义时,最好先讲解一下极限的漫长发展史,介绍一些典型的例子,从而让学生更好的理解极限的这种数学语言定义,并激发他们的学习兴趣。数列极限定义的一个最主要的应用就是验证极限的存在性,这也是教学中的难点,只有理解好定义,才能熟练掌握这种验证方法。
分析:利用极限的定义验证极限值,最关键就是要把定义理解好,在ε-N语言中,ε是预先给定的,主要是将N找到,而N的取值一般由ε决定。
1.2 函数极限定义
(1)x→x0时函数 f(x)的极限。
设函数f(x)和常数A,如果对于任意给定的ε>0,必存在δ>0,使当时,总有不等式成立,则称常数A为x→x0时函数f(x)的极限,记为,或 f(x)→A(x→x0)。
(2)x→∞ 时函数 f(x)的极限。
设函数f(x)和常数A,如果对于任意给定的ε>0,必存在 X>0,使当时,总有不等式成立,则称常数A为x→∞时函数f(x)的极限,记为,或 f(x)→A(x→∞)。
以上两个定义均为函数的双侧极限定义,同理可以定义单侧极限,分别为时的函数 f(x)的极限.接下来,我们看一下关于极限定义应用的一个典型例子。
例 1:设函数 f(x)在(-∞,+∞)上可导,并且满足 f(0)≤0,证明:存在 ξ1∈(-∞,0)和 ξ2∈(0,+∞),使得 f(ξ1)=2019=f(ξ2)。
分析:本题从问题出发,初步判定是零点存在问题,先构造函数,但直接可利用的条件只有一条,即条件不充足,所以从极限这个条件出发创造条件,从而应用零点存在定理即可得出想要的结论,具体如下。
证:令 F(x)=f(x)-2019,函数 f(x)在(-∞,+∞)上可导,所以 F(x)在(-∞,+∞)上连续,且 F(0)=f(0)-2019<0,因,由极限的定义,必定存在 X>0,当时,使得 f(x)>2019,即 F(-X)=f(-X)-2019>0,F(0)<0。
由零点存在定理,存在 ξ1∈(-X,0)∈(-∞,0),
使得 F(ξ1)=f(ξ1)-2019=0,即 f(ξ1)=2019,
同理,F(X)=f(X)-2019>0,F(0)<0 存在 ξ2∈(0,X)∈(0,+∞),
使得 F(ξ2)=f(ξ2)-2019=0,即 f(ξ2)=2019。
所以存在 ξ1∈(-∞,0)和 ξ2∈(0,+∞),使得 f(ξ1)=2019=f(ξ2)。
分析:函数f(x)是分段函数,在分段点处的极限通常采用单侧极限定义进行讨论,当左右极限都存在且相等时,可得出函数在该点极限存在且为同一个数,否则,极限不存在。
2.连续定义及其应用
连续是微积分中继极限之后的一个重要研究对象,极限是它定义的一个基础性条件.连续是可导,可微分的必要条件,也是极限存在,可积的充分条件,所以学好函数的连续问题,是学好高等数学至关重要的一个环节.关于函数连续的定义主要有以下几种:
函数f(x)在点x0及其邻域内有定义,则函数在点处连续的定义有如下四种互相等价的描述:
这个式子有三层含义:一是蕴含着函数f(x)在点x0有定义;二是表示极限存在;三是极限值等于函数值f(x0).这三层意思缺一不可,否则就是间断点。
(3)在 x=x0处连续是指:既(左连续),又(右连续)。
这几个定义是等价的,一般情况下,第一个定义在实际问题计算和讨论时应用的较多,而证明函数的连续性问题时往往用第二个定义多些,分段函数在分段点处的连续性的讨论与判定多数采用第三个定义,即讨论左右连续与连续的关系。
例1:设函数f(x)在x=0处连续,且对x,y任意有关系式f(x+y)=f(x)+f(y),
求证:f(x)在上连续(-∞,+∞)。
证明:对任意 x,y∈(-∞,+∞)有关系式 f(x+y)=f(x)+f(y),令 x=y=0,则f(0)=2f(0),即 f(0)=0.进而,任意 x∈(-∞,+∞),作改变量△x,则有:,
所以 f(x)在(-∞,+∞)上连续。
例2:设函数f(x)是定义在[a,b]上的严格单调增加函数,对点x0∈(a,b),极限存在,证明:函数f(x)在x0处连续。
证明:已知函数f(x)在[a,b]上的严格单调增加,根据极限保号性分别有:
当 x<x0时,f(x)<f(x0),从而,
当 x>x0时,f(x)>f(x0),从而,
所以函数f(x)在x0处连续。
解:(1)f(1)=12=1,又,右连续,(2x-1)=1=f(1),左连续,所以函数f(x)在点x=1处连续。
(2)f(2)=22=4,又,右不连续,
3.导数定义及其应用
导数是微积分的重要研究对象,它是研究变化率的问题,有着非常广泛的应用,为我们解决实际问题提供了很好的研究工具。
定义:设函数f(x)在点x0的某邻域内有定义,当自变量在x0处取得改变量△x(△x≠0)时,函数相应地取得改变量△y=f(x0+△x)-f(x0),如果极限存在,则称函数f(x)在点x处0可导,记为。
若将变化趋势x→△x改为相应的x→△x+(x→△x-),则称为相应的右导数(左导数),分别记为,且有函数在x0处可导的充要条件:f'(x0)存在,通常用该定理判断分段函数在分段点处是否可导。
在微积分中,我们知道导数的应用非常广泛,如利用导数可以研究函数的单调性、图像的凹凸性、极值与最值等问题.除此之外导数定义本身的应用也是非常重要的,如下面的实例。
例1:已知f'(x0)=5,求解极限①;②。
分析:利用导数定义求相应的极限问题是导数定义应用的一个典型。
②分解变形

例 2:设函数 f(x)=(x2018-1)g(x),其中 g(x)在 x=1处连续,且 g(1)=1,求f'(1)。
分析:因为此题不知道f(x)的解析式,所以不能利用先求导函数,再带入1求f'(1),故只能从导数定义出发进行求解。
解:根据导数定义可得:
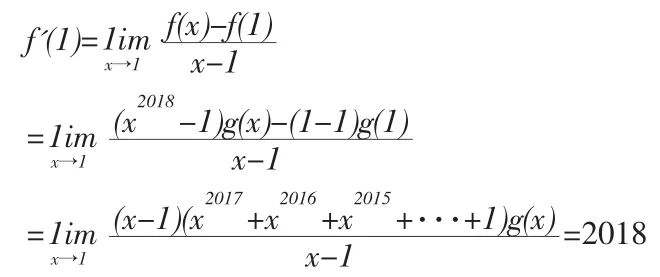
例3:设函数 f(x)在点x0处连续,且在点x0处可导,证明:函数f(x)在点x0处可导,并求f'(x)。(第18届大连市数学竞赛)

(2)若 f(x0)=0,
综上,函数f(x)在点x0处可导,且:

4.定积分的定义及其应用
定积分是积分学中一个重要研究对象,在实际问题中有着非常广泛的应用,特别是在几何学和物理学中,如可以求解不规则图形的面积、旋转体的体积、变力沿直线所作的功、水压力、引力等实际问题,而定积分的定义本身也有一定的研究价值和应用。
定义:设函数f(x)在区间[a,b]上有界,在[a,b]中任意插入n-1个分点,记作 a=x0<x1<x2<···<xn-1<xn=b。
这样就把区间[a,b]任意分成个 n小区间[x0,x1],[x1,x2],···[xn-1,xn],每个小区间的长度为△xi=xi-xi-1,其中i=1,2···n,在每个小区间[xi-1,xi]上任取一点 ξi(xi-1≤ξi≤xi),作乘积 f(ξi)△xi(i=1,2···n),在求和,令 λ=max{△x1,△x2,···△xn},若当 λ→0 时,无论区间怎样分割,无论ξi怎样选取,若上述和式的极限都存在,则称此极限值就是函数f(x)在区间[a,b]的定积分,记作:。
定积分研究的是一种特殊和式的极限问题,因此我们可以逆向思考,如果碰到类似这样的和式极限问题,我们可以将其转化为定积分求解,这也是微积分中求解极限的一个典型方法.利用定积分定义求解极限关键之处在于通过和式结构确定定积分的被积函数和积分上下限,因此要求学生们对定积分的定义要理解透彻,这样才能够准确地求解出极限来。
解:首先将上述和式转化为黎曼和式,即定积分定义中和式结构。

分析:相比较,此题的难度大些,但处理方法同上,首先将给出的和式变形再进行分析求解。
这里的和式,可以看成是函数sinx在区间[1,b]上按分划,即:
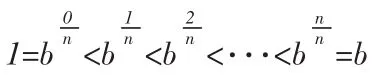
综上,我们通过对一元微积分中重要概念的研究和典型例子分析可知,在学习微积分的过程中,对于每个新接触的概念定义,我们不仅要掌握它的一般形式,更应懂得它的内涵,将其理解透彻,只有这样,才能掌握怎样应用定义去解决相应的问题的方法,并举一反三,从而学好微积分,也为后续的学习打下良好的基础。

