基于切深模型的汽车曲轴轴颈巴厘线磨削精度控制
上海大学 李 静 高华钰 沈南燕 方明伦
上海机床厂有限公司 黄海涛
汽车曲轴作为发动机关键零件,其主轴颈、连杆颈巴厘线的磨削精度对发动机性能有较大影响。切入磨削过程中,成形砂轮轮廓将直接反映在曲轴轴颈上,因此研究了基于砂轮修整切深模型的成形砂轮廓形修整误差在线测量及补偿方法,通过控制砂轮廓形修整精度来保证曲轴轴颈巴厘线的磨削精度。采用声发射传感器搭建了砂轮修整过程监测系统,建立了砂轮圆弧修整过程中任意位置的声发射信号均方根值与修整切深的数学模型。通过构建切深模型参数与修整进给速度和修整圆弧中凸量的函数关系,得到了砂轮圆弧修整变参数切深模型,提高了切深模型的准确性。在此模型的基础上,提出了砂轮廓形修整误差补偿策略及实现流程。实验证明:采用变参数切深模型可以准确获得砂轮实际修整廓形,定量评定砂轮廓形修整误差,并且修整误差补偿策略能够有效地保证巴厘线廓形磨削精度。
一、 前言
曲轴是汽车发动机上的关键零件之一,需求量大,组成要素多,轮廓形状复杂,精度要求高。曲轴轴颈圆柱表面母线为具有一定公差要求的圆弧形,主轴颈呈凸形,连杆颈呈凹形,称为巴厘线(源自德文Ballig)。主轴颈巴厘线能避免高扭矩状态下的曲轴轴颈与轴瓦出现边角接触;而连杆颈巴厘线则对动压油膜的建立有利,从而提升发动机可靠性[1]。因此曲轴主轴颈、连杆轴颈巴厘线的磨削精度对发动机性能有较大影响。
巴厘线通常是通过对砂轮进行成形修整,再由切入磨来实现的。国内的李小新等[2]提出采用矢量切点式跟踪磨削的方法,通过改造砂轮基体结构以及磨削时调整砂轮线速度实现曲轴巴厘线的磨削。该方法不能够很好地控制巴厘线形状及尺寸,且不易操作,因此实用性不高。目前广泛应用的曲轴随动磨削技术,通过控制C轴和X轴的联动实现一次装夹对所有主轴颈和连杆颈的磨削[3-4],并利用成形砂轮磨削出曲轴轴颈巴厘线。因此,高效率大批量生产中汽车曲轴轴颈巴厘线的中凸或中凹量主要靠砂轮廓形的修整精度保证。
砂轮廓形在机修整通过Z-X轴联动的圆弧插补实现[5],但由于曲轴磨床加工需求和配置特点,通常采用伺服电机驱动配合滚珠丝杠传动实现沿工件轴向的Z轴移动,其运动定位精度相对采用直线电机直驱的砂轮架进给方向的X轴明显较低,导致磨床Z-X联动插补精度较低,由此降低了砂轮轮廓的修整精度,产生曲轴轴径巴厘线加工误差。
因此,在生产节拍快、连续工作周期长的汽车发动机生产线用曲轴磨床上,为保证曲轴轴颈巴厘线的加工质量及稳定性,需要监测砂轮修形过程,以便及时补偿砂轮轮廓的修整误差,保证修整精度和修整效率。声发射(Acoustic Emission, AE)信号因其高频的特点,可避开低频噪声的干扰且灵敏度极高,已被广泛应用于对工件磨削及砂轮修整过程的监控[6-11]。但此方面研究大多集中在利用声发射信号进行定性分析,如砂轮磨损状态判别[8-9]以及砂轮修整时与修整器的接触状态判别[10-11],而没有定量分析声发射信号与砂轮修整廓型的对应关系。
本文通过构建砂轮修整监测平台,定量分析不同修整参数下声发射信号的特征值与修整切深之间的关系,从而通过修整过程中的声发射信号廓形得到砂轮实际修整廓形的估计值,进而获得廓形中凸量修整误差。以此为基础,研究修整廓形中凸量补偿策略,达到通过控制砂轮廓形修整精度保证曲轴轴颈巴厘线磨削精度的目的。
二、巴厘线磨削精度控制系统方案
曲轴轴颈巴厘线的磨削精度主要靠砂轮廓形精度保证,切入磨削过程中砂轮廓形将直接反映在曲轴轴颈上。因此可以通过控制砂轮廓形的修整精度,来满足曲轴轴颈巴厘线磨削精度。为此,本文设计了如图1所示的砂轮廓形修整精度控制系统方案:通过布置在修整器附近的声发射传感器及相关采集设备实时获取砂轮修整过程中的声发射信号;在滤波等信号预处理的基础上,基于某位置附近微小时段声发射信号均方根值与该位置实际修整切深之间的数学模型,对砂轮实际修整廓形进行在线估计;根据砂轮实际修整廓形与理论修整廓形,计算补偿后的砂轮修整圆弧半径,并更新具有中凸量误差补偿能力的砂轮修整NC程序;最后通过CNC系统执行此修整程序,以此保证砂轮廓形修整精度,从而实现曲轴轴颈巴厘线磨削精度在线控制。

图1 砂轮廓形修整精度的控制系统
三、基于声发射信号的砂轮圆弧廓形修整切深建模
轴颈巴厘线廓形通常为圆弧,该圆弧的弦高即为巴厘线的中凸或中凹量。砂轮的理论修整廓形与工件巴厘线廓形相同。通过在机直接测量获得砂轮廓形的修整质量十分困难[12],因此采用声发射(AE)信号,在砂轮修平的基础上,通过研究AE信号与修整切深间的数学模型,用某位置附近微小时段的AE信号均方根值来表征该位置的修整切深,进而获得砂轮实际修整圆弧廓形,实现其在机间接测量。
1. 砂轮平修切深模型
磨削过程AE信号的均方根值与法向或切向磨削力的变化曲线相近[13-14],在外圆切入磨削过程中AE信号均方根值与磨削力成一定的比例关系[15-16]。
而修整过程中修整器与砂轮之间的相互作用与磨削过程中砂轮与工件的关系相似,因此修整过程中AE信号的均方根值与修整力之间也有类似的关系。借鉴磨削力的经验公式[17],砂轮修整过程中AE信号的均方根值与砂轮修整参数具有类似的函数关系,其表达形式如下:

式中,
Xae——AE信号均方根值/V;
Xgr——修整切深/mm;
Fz——Z方向进给速度/mm·min-1;
Vs——砂轮转速/m·s-1;
a0 、a1 、a2 、a3——待定参数。
将式(1)变形,则修整切深可表示为

经简化得砂轮平修时的切深模型:

在圆弧修整过程中,圆弧中凸量相较于圆弧半径r非常小,基于微元法的思想,将每一微小时段看作是沿Z轴方向的平修。如图2所示, 为修整圆弧轨迹,C为圆弧最高点,O为圆弧圆心,D为CO与AB的交点。已知修整圆弧中凸量=ap,修整圆弧宽度在直角△OAD中,满足如下关系:

得圆弧半径:

若以A为圆弧起点,某时刻修整到P点,修整器沿Z方向运动了zi距离,此时对应的圆心角θ满足如下关系:

根据图中的几何关系,进给速度F与Z轴也呈θ角,其Z轴分量:

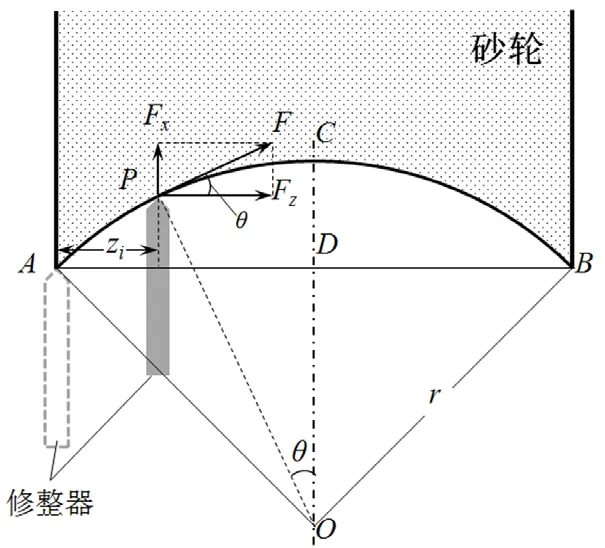
图2 圆弧修整原理几何示意
由式(5)~(7)可得圆弧轨迹中任意位置zi处的Z方向进给速度

将式(8)代入式(3),即可得到该位置砂轮圆弧修整的切深模型。
四、砂轮圆弧廓形修整切深模型的改进
1 .砂轮圆弧廓形修整切深模型参数辨识
砂轮圆弧廓形修整过程中,AE信号均方根值及Z方向进给速度均在变化,而砂轮转速始终为恒定值,因此切深模型中与砂轮转速有关的一项也为常系数项,可将该项与常系数项 1合并处理,由此式(3)的切深模型将简化为:
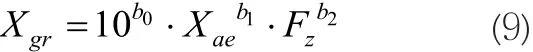
式中,b0为合并后的常系数项指数,为原b0与b3lgVs之和。
令上式两边分别取对数,将该非线性模型转换为线性模型,得到:

则各参数的求解可转换为多元线性回归方程系数的求解。根据修整进给速度F、修整圆弧中凸量ap、修整圆弧宽度d,利用式(8)计算出各位置Z方向进给速度Fz。同时联立修整过程中各位置附近微小时段内的AE信号均方根值Xae及实际修整廓形测量值Xgr作为样本输入模型,基于最小二乘的原则,将求得的式(10)中系数最优值作为砂轮圆弧廓形修整切深模型参数辨识结果。
但由于圆弧修整过程的复杂性,如不同修整参数产生的系统伺服误差不同等,使得不同修整参数求解得到的模型参数不尽相同。若直接将模型参数定为常数,则模型准确性不佳。因此本文将通过分析并建立模型参数与修整参数的关系,来改进砂轮圆弧廓形修整切深模型。
2.修整参数对模型参数的影响
为了探究不同修整参数对模型参数的影响,并对切深模型进行改进,本文设计了单因素试验进行分析。对标实际生产中的主轴颈巴厘线磨削,即欲将工件磨成中凸廓形,砂轮相应地需修整成中凹廓形。为了保证修整切深与廓形的准确映射,每次砂轮圆弧廓形修整之前应保证砂轮已修平。
实际应用中,砂轮转速通常根据砂轮类型和磨床能力选定后无需调整。因此本文不考虑砂轮转速变化的影响,将模型参数b0、b1、b2均看作是进给速度F及修整圆弧中凸量ap的函数。为此,本文分别设计了中凸量为6μm、进给速度在40mm/min~150mm/min范围变化的单因素试验及进给速度为100mm/min、中凸量在1~12μm范围变化的单因素试验。试验过程中砂轮转速恒定为30m/s。基于上小节中的参数辨识方法,根据试验结果求解得到的参数及其变化趋势分别如图3、图4所示。其中图3为仅进给速度变化时模型参数变化趋势,图4为仅圆弧中凸量变化时模型参数变化趋势。
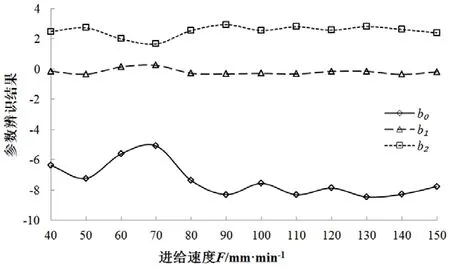
图3 进给速度变化时参数变化趋势
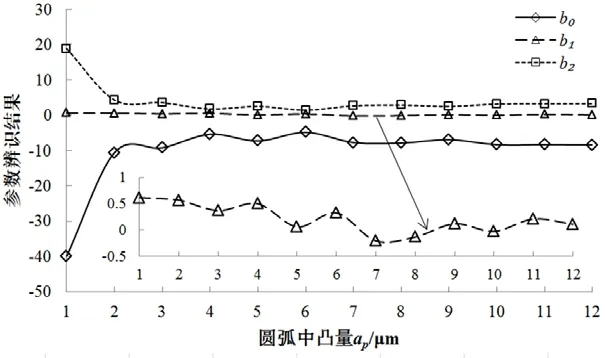
图4 圆弧中凸量变化时参数变化趋势
图3结果表明:进给速度在40mm/min至150mm/min之间变化时,参数b1与b0变化趋势相同而与b2变化趋势相反,三个参数的变化规律基本相同:进给速度在50mm/min至80mm/min之间变化时,参数变化剧烈,在60mm/min至70mm/min间出现最值;其余位置变化平缓,基本呈高斯函数变化趋势。图4结果表明:圆弧中凸量在1~12μm之间变化时,参数b1与b2变化趋势相同而与b0变化趋势相反,三个参数的变化规律基本相同:中凸量在2μm以下时,参数有明显下降(上升),在2μm以上时则变化平缓,基本呈幂函数变化趋势。
3. 砂轮圆弧修整变参数切深模型
基于上节分析,分别以高斯函数及幂函数为基础,以二次多项式补充修正,对两组单因素试验的参数变化曲线进行拟合,进而建立砂轮圆弧修整变参数切深模型。
若记:

则可将参数曲线拟合函数表示为以下形式:

为提高切深模型的准确性,设计了如图5所示的砂轮圆弧修整变参数切深模型参数辨识流程:对模型估计相对误差进行补偿,计算产生新的参数,再进行参数曲线拟合,直至模型估计相对误差小于误差限10%,可实现基于模型估计误差的参数识别结果自调整。其中新的参数基于以下规则产生:

由于模型中包含参数b0的一项为常系数项,为方便计算,将模型估计误差全补偿至b0,则产生的新参数值为

式中j表示参数调整次数,j=0、1、2、……。其中b0(0)、b1(0)、b2(0)为上节中得到的参数。

图5 砂轮圆弧修整变参数切深模型参数辨识流程
最终求得拟合后结果为

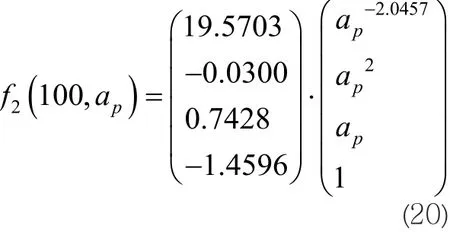
依据参数拟合函数的基本函数构成,可将上述单因素试验结果进行整合,假定切深模型各参数具有如下数学表达形式

式中Bi为 的系数矩阵,i=0、1、2…
根据式(15)~(21)即可求得参数b0、b1、b2的系数矩阵B0、B1、B2,从而可得到b0、b1、b2关于进给速度F及修整圆弧中凸量ap的函数表达式,进而代入式(9)可得到砂轮圆弧修整任意位置变参数切深模型:


五、砂轮修整廓形精度控制策略
1.砂轮圆弧修整中凸量误差补偿规则
根据修整过程中砂轮宽度上各位置得到的AE信号均方根值,由建立的砂轮圆弧修整变参数切深模型,可以获得连续的砂轮实际修整廓形。与砂轮理论修整廓形对比,可以发现实际修整廓形仍近似为圆弧,砂轮修整廓形误差整体反映在圆弧的中凸量上。由于存在伺服滞后误差以及修整笔磨损等原因,实际修整廓形的中凸量总是小于理论修整廓形,中凸量绝对误差(即模型估计得到的实际中凸量与理论中凸量的绝对误差) 。因此保持修整圆弧起点和终点不变的情况下,本文通过增大修整程序中的圆弧轨迹半径来实现砂轮廓形中凸量的补偿。
如图6所示,虚线表示补偿前后的理论修整廓形,而实线表示补偿前后的实际修整廓形;为补偿前的理论修整廓形,其圆弧圆心位于O点,圆弧中凸量=a;为补偿后的理论修整廓形,其圆弧圆心位于O′点,圆弧中凸量=ap′。根据几何关系得到的补偿前的理论圆弧半径为:
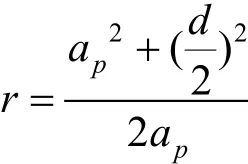
将补偿前后理论圆弧廓形中凸量的增量设定为与补偿前的中凸量绝对误差值ε相等如图所示,补偿后的理论圆弧中凸量变为,得因此补偿后的理论圆弧半径:


图6 中凸量误差补偿原理几何示意
基于上节单因素试验,进行中凸量误差补偿试验,补偿前后试验结果如表1所示:

表1 中凸量误差补偿试验方案及结果
试验结果表明:补偿前,实际中凸量与理论中凸量相对误差较大,多数都在20%以上;而补偿后,实际中凸量与理论中凸量的相对误差均控制在5%以内,补偿效果良好。
2.砂轮廓形修整误差补偿流程
根据汽车曲轴巴厘线磨削精度控制方案,本文设计了如图7所示的砂轮圆弧修整中凸量误差补偿流程。其中中凸量相对误差δ的范围设定由以下规则确定:
已知实测廓形的相对误差δms(即实测廓形中凸量ap测量量与理论中凸量ap的相对误差)满足:
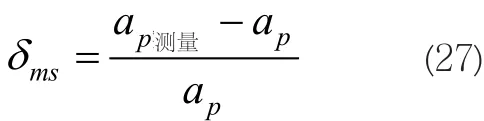
模型估计相对误差δpr(e即估计廓形中凸量与实际测量得廓形中凸量的相对误差)满足:

中凸量相对误差δ(即由模型估计得到的实际修整廓形中凸量与理论中凸量ap的相对误差)满足

结合式(27)~(28)得


图7 汽车曲轴巴厘线磨削精度控制流程
六、巴厘线磨削精度控制实验验证
为了完整验证轴颈巴厘线磨削精度控制方案的有效性,在偏心轴非圆磨床H367上进行了验证实验。如图8所示,实验以圆棒代替实际生产中的主轴颈,声发射传感器利用磁座吸附在修整点附近进行修整过程中AE信号的获取;根据砂轮修整廓形中凸量精度控制流程进行砂轮圆弧廓形修整后,对工件进行外圆切入磨削,将砂轮廓形印刻在工件上;磨削完成后,工件转移至SE13-J10曲轴测量机上进行实际修整廓形的测量。实验随机选取了七组修整参数,实验条件见表2。

图8 巴厘线磨削精度控制验证实验
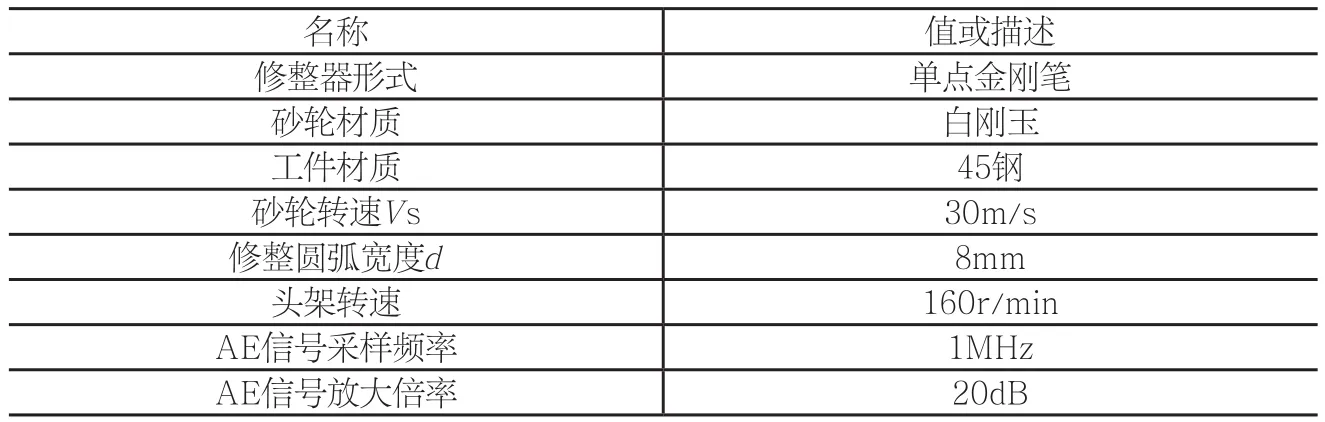
表2 中凸量误差补偿试验方案及结果
在砂轮修整过程中,传感器采集的信号并不只包含由于砂轮修整而产生的有效信号,而是各种噪声与试验有效信号的交叠,对试验结果会造成影响。鉴于噪声和有效信号往往具有不同的频率分布特性,通过快速傅里叶(FFT)频谱分析[18],对比修整前与修整时声发射信号频谱的变化,确定砂轮修整时的有效信号的频段分布范围集中在100kHz到225kHz之间。
声发射的信号强度一般选用其均方根值来表征,见式(31)。式中V(t)为任意时刻采集的声发射信号值,T为时间常数。本文取时间常数为100ms。

验证实验结果如表3所示,试验结果表明,最终廓形误差均控制在10%以内,验证了砂轮圆弧修整切深模型的正确性,以及轴颈巴厘线磨削精度控制方案的可行性。

表3 巴厘线磨削精度控制验证实验
七、结论
为实现曲轴轴径巴厘线磨削精度控制,研究了成形砂轮廓形修整误差在线监测及补偿方法,具体包括:
(1)通过类比磨削力模型,建立了基于声发射信号的砂轮圆弧修整切深模型,从而获得了修整过程中声发射信号廓形与砂轮实际修整廓形之间的定量关系,利用声发射信号估计出砂轮实际修整廓形。
(2)为提高切深模型的准确性,基于单因素试验结果,分析模型参数随修整进给速度和修整圆弧中凸量的变化规律,发现模型参数随前者的变化基本呈高斯函数形式,随后者变化基本呈幂函数形式。以此为基础,构建了砂轮圆弧修整变参数切深模型,并设计了模型参数辨识流程及参数产生规则,实现了基于模型误差的参数自调整。
(3)通过分析实际修整廓形,确定廓形误差主要体现在圆弧中凸量上,由此提出通过改变修整圆弧半径进行补偿的规则。并设计了砂轮圆弧修整中凸量误差自动补偿流程。
上述砂轮圆弧修整变参数切实模型及中凸量误差补偿策略,通过实际修整及磨削实验,验证了其在巴厘线磨削精度控制中的有效性。在具体应用中,由于声发射传感器安装位置对采集信号有一定影响,因此下一步将对不同安装位置采得信号对切深模型参数的影响进行研究,以增强模型的鲁棒性。

