冷弯薄壁C型钢-泡沫混凝土组合楼板弹性抗弯极限承载力分析

刘殿忠 贾景超 刘婉娟

(吉林建筑大学 土木工程学院,长春 130118)

随着国家建筑节能政策的推行和建筑物高层、大跨的走势,对建筑材料的综合性能要求越来越高.泡沫混凝土作为多孔材料中的一种,轻质高强,具有良好的保温隔热、隔音耐火、节能利废等性能.冷弯薄壁型钢通过优化截面形状来提高钢材的利用率,且制作、施工、运输、安装简便,是一种经济高效节能的材料.本文将冷弯薄壁型钢埋置于泡沫混凝土中形成组合板,二者共同承受外部作用.

组合单向板在弯矩作用下,底部受拉区边缘纤维达到泡沫混凝土的极限拉应变后,泡沫混凝土受拉开裂,并退出工作,组合单向板进入到弹塑性工作状态,取开裂弯矩作为组合单向板的弹性抗弯极限承载力[1].

1 组合单向板弹性抗弯极限承载力计算

组合单向板采用沿板跨方向布置的冷弯C型钢为骨架,型钢之间采用钢拉条拉结,浇筑泡沫混凝土后形成组合单向板,组合单向板的组成形式如图1所示.

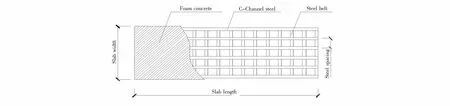
图1 组合单向板组成(单位：mm)Fig.1 Composition of composite one-way slab

基于弹性理论,采用换算截面法建立组合单向板的弹性抗弯极限承载力的计算公式为简化计算,作如下基本假定:① 符合平截面假定;② 忽略泡沫混凝土和冷弯型钢之间的相对滑移;③ 钢材与泡沫混凝土均视为理想弹性材料.

依据上述假定,取一个型钢间距作为计算单元,建立组合单向板的计算模型如图2所示.将冷弯型钢截面换算成泡沫混凝土截面进行计算,换算系数为二者的模量比αE,即αE=Es/Epc,其中,Es为冷弯型钢弹性模量,Epc为泡沫混凝土弹性模量.

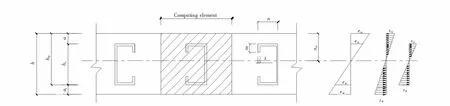
图2 组合单向板计算模型(单位：mm)Fig.2 The calculation model of composite one-way slab

计算弹性抗弯极限承载力时的受压区高度xcr,可由受拉区及受压区对中和轴的面积矩相等得到:

(1)

式中，xcr为受压区高度，mm；h为板的厚度，mm；h0为板截面的有效高度，mm；as为C型钢受拉区保护层厚度，mm；a为C型钢受压区保护层厚度，mm；hs为C型钢高度，mm；b为计算单元的宽度，mm；m为C型钢卷边长度，mm；t为C型钢厚度，mm；n为C型钢翼缘宽度，mm；αE为钢材与泡沫混凝土的弹性模量比；σct为泡沫混凝土拉应力，MPa；σcc为泡沫混凝土压应力，MPa；σst为C型钢拉应力，MPa；σsc为C型钢压应力，MPa；εcc为泡沫混凝土压应变，με；εct为泡沫混凝土拉应变，με；εsc为C型钢压应变，με；εst为C型钢拉应变，με.

对受压区混凝土合力点取矩可得开裂弯矩——弹性抗弯极限承载力:

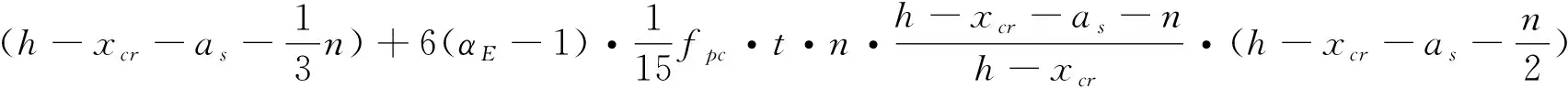
式中,fpc为泡沫混凝土抗压强度,MPa；其他参数同上.

2 组合单向板弯矩-曲率关系

采用有限条带法分析计算组合单向板的弯矩-曲率关系.将组合单向板截面划分为有限的条带,进行合成迭代计算.以泡沫混凝土压应变达到极限应变值作为破坏的判别条件[2],计算组合单向板的承载能力.

2.1 材料的本构关系

文中采用颜雪洲博士[3]给出的泡沫混凝土本构关系模型为两段曲线;冷弯C型钢的应力-应变关系采用理想弹塑性模型,不考虑应变强化,钢材的屈服强度为fy=235MPa,弹性模量Es=2.06×105MPa.

2.2 计算原理

将组合单向板跨中截面沿高度划分成有限条带,如图3所示.计算假定如下:① 截面的平均应变沿截面高度线性分布;② 冷弯C型钢与泡沫混凝土之间无相对滑移;③ 每个条带内的应力均匀分布.

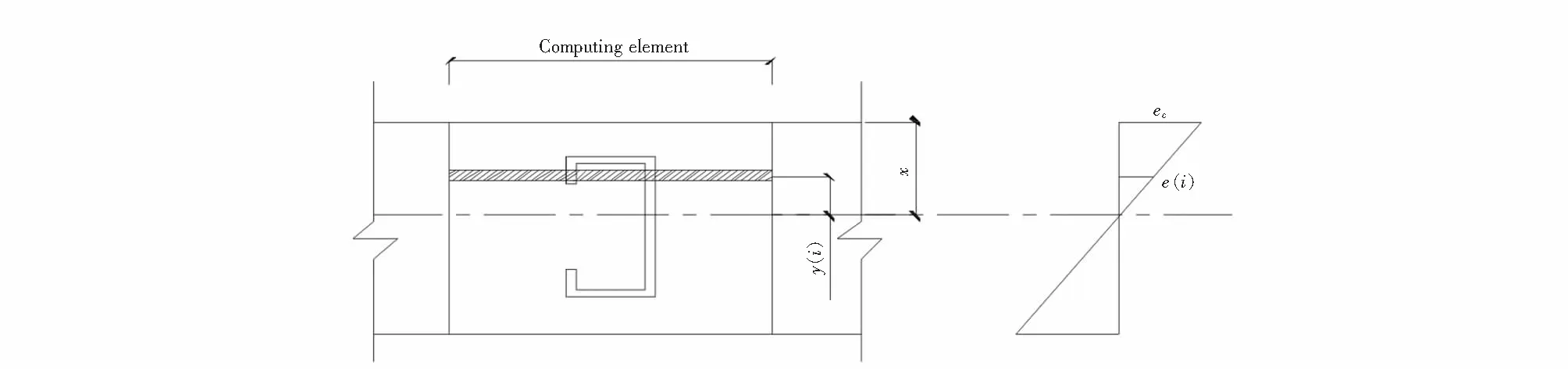
图3 组合板截面有限条带示意图Fig.3 Schematic diagram of finite strip of composite slab section

由平截面假定,根据几何条件可知:

由假定泡沫与型钢之间无滑移可知εci=εsi,由本构关系得到相应的泡沫混凝土和冷弯型钢的应力σci和σsi.则相应的第i条带所承受的冷弯型钢与泡沫混凝土的作用力分别为:

Nci=Aci·σci,Nsi=Asi·σsi

式中，Nci为第i条带所承受的泡沫混凝土作用力，N；Nsi为第i条带所承受的C型钢作用力，N；Aci为第i条带混凝土面积，mm2；σci为第i条带混凝土应力，MPa；Asi为第i条带C型钢面积，mm2；σsi为第i条带C型钢应力，MPa.

式中，yci为第i条带混凝土形心到中和轴距离，mm；ysi为第i条带C型钢心到中和轴距离，mm.

2.3 计算步骤

根据上述计算公式,采用Matlab语言编程计算,具体计算步骤如下:

(1) 输入组合单向板的基本数据,初始条件假定中和轴位于组合单向板板底,给定中和轴的上移增量.

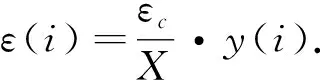
(3) 计算截面各条带内力总和,判别是否满足误差要求.若不满足,采用二分法重复第(1)和(2)步计算,直到满足精度要求为止.

(4) 根据迭代得到符合条件的每一组的ε,φ和M.

(5) 循环步骤(1)～(4),可得到截面的弯矩和曲率关系曲线[4].

针对图5的组合单向板,泡沫混凝土分别采用800kg/m3,1 000kg/m3,1 200kg/m3和1 600kg/m3等4种密度,其泡沫混凝土的力学性能指标参考文献[5],针对不同密度下组合单向板可画出其弯矩-曲率关系全过程曲线.

3 试验与模拟分析

为研究轻钢与泡沫混凝土组合楼板承载能力,设计制作了2块组合板,板内型钢骨架采用冷弯薄壁C型钢,其型号为C100×50×2.0mm;泡沫混凝土密度为1 200kg/m3;其中一块在钢拉条上设有栓钉、一块无栓钉.试验采用跨中两点对称加载,组合楼板试件如图4所示.组合楼板试验过程如图5所示.

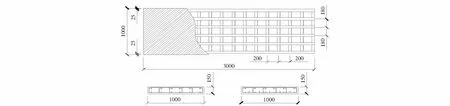
(a) B-1 no stud (b) B-2 with the stud图4 组合楼板试件(单位：mm)Fig.4 Composite floor specimens

(a) Composite floor loading (b) Diagonal crack图5 组合楼板试验Fig.5 Composite floor test

由图6的荷载-挠度曲线可知,当荷载达到极限荷载的25%左右时,曲线处于弹性阶段,两块板的挠曲线在弹性阶段的部分基本重合,此时,泡沫混凝土与型钢能较好的共同工作.荷载继续增加后,板底部泡沫混凝土开始出现裂缝,当荷载达到极限荷载的45%左右时,裂缝宽度达到0.22mm,组合楼板跨中挠度达到了跨度的L/200,曲线处于弹塑性阶段, 两条曲线并没有出现明显的转折,但裂缝的发展导致挠曲线的斜率变小；当荷载达到极限荷载的75%左右时,型钢受拉翼缘开始屈服,裂缝数量增多、宽度加宽,受压区的泡沫混凝土应力也逐渐增大,挠度增长明显加快,组合楼板进入塑性阶段.当荷载达到极限荷载时,型钢受压翼缘已经屈服、泡沫混凝土被压碎,组合楼板弯曲破坏.由于只在钢拉条上设有栓钉,且每个型钢间距内只设有一个栓钉,试验结果表明,此处设置栓钉对组合单向板的承载力和挠度影响不大,原因是钢拉条自身刚度小,对型钢骨架的约束有限.

图7是组合楼板纯弯段泡沫混凝土沿截面高度的应变曲线,图8是组合楼板沿C型钢截面高度的应变曲线,C型钢与泡沫混凝土组合楼板沿截面高度的应变基本符合平截面假定.在加载过程中,随着荷载增加中和轴略有上移.当荷载接近极限荷载时,其拉应变增长迅速,受拉区塑性进一步开展;而C型钢受拉翼缘屈服后,腹板和受压翼缘尚未屈服,中和轴略有上升,荷载继续增加,型钢腹板渐渐屈服,应变不再呈线性变化,达到极限荷载时C型钢受拉翼缘及腹板的受拉部分基本达到屈服.

由于篇幅所限,对于组合单向板的有限元模拟分析以及弯矩-曲率法的计算过程等内容文中不作详细叙述,只是引用其具体计算结果与试验结果进行对比.

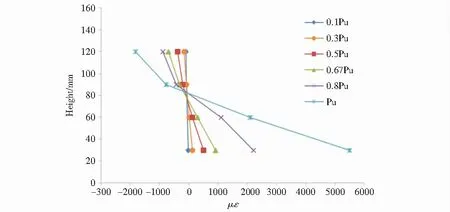
图7 跨中泡沫混凝土沿截面高度应变Fig.7 Middle span foam concrete along section height strain

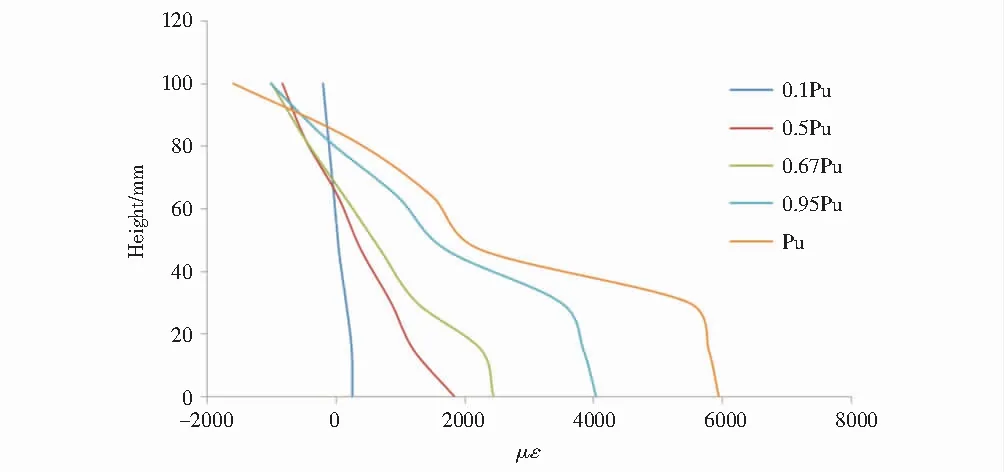
图8 型钢沿截面高度应变Fig.8 Steel sections strain along section height

图9为组合楼板试验结果与ABAQUS有限元模拟结果的荷载-挠度曲线对比,试验曲线与模拟曲线基本,二者吻合较好.

图10和图11分别是C型钢上翼缘和下翼缘的应变曲线对比,图12为受压区泡沫混凝土应变曲线对比.

图9 试验与模拟荷载-挠度曲线Fig.9 Test and simulate load-deflection curve

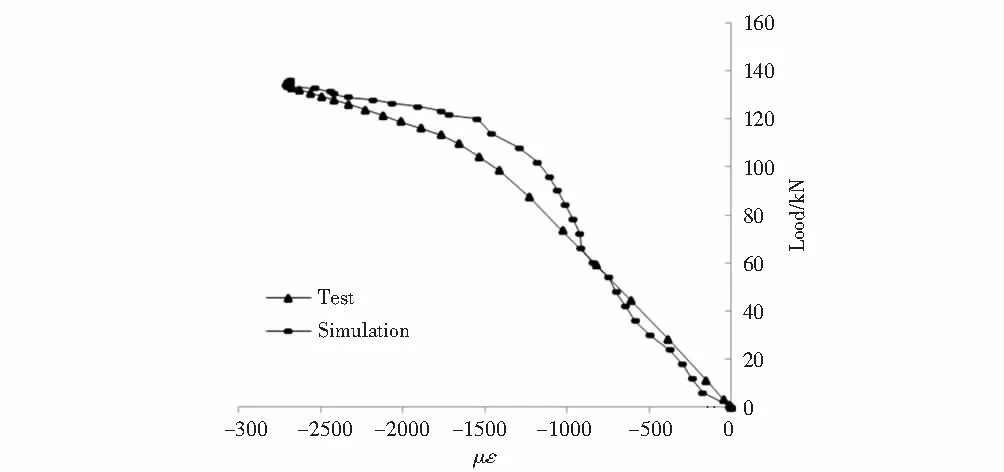
图10 型钢上翼缘应变曲线对比Fig.10 Upper flange strain curve

上述曲线对比结果表明，模拟分析结果与试验结果基本一致,同时也进一步验证有限元模型的正确以及模拟分析的准确性.将组合板弹性抗弯极限承载力与试验值(B-1)、数值模拟值进行比较,结果详见表1.换算截面法计算结果与试验值、数值模拟值均比较接近.

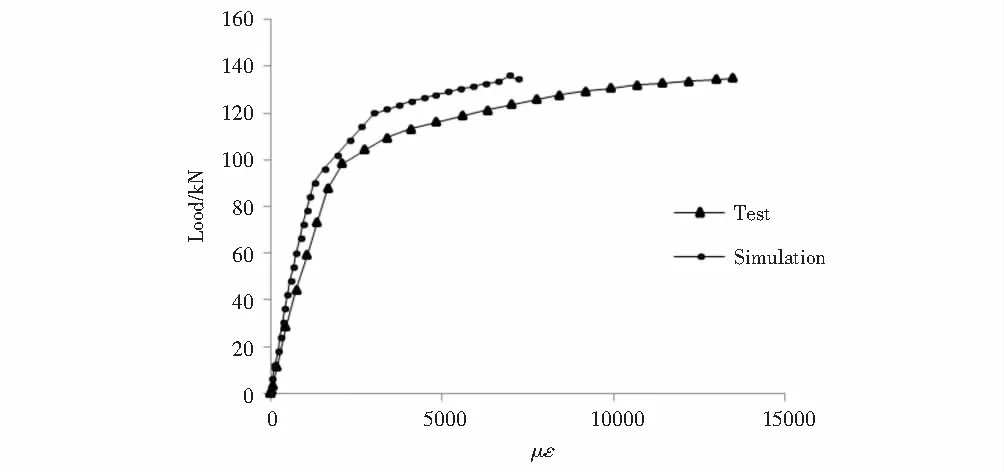
图11 型钢下翼缘应变曲线对比Fig.11 Bottom flange strain curve comparison

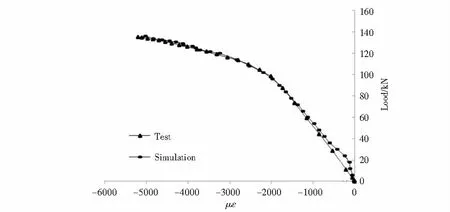
图12 泡沫混凝土应变曲线对比Fig.12 Foam concrete strain curve comparison

Test(B-1)SimulationFiniteCurvatureTrans formed sectionTheoryTestFinite/TestCurvature/Test11.8610.9913.1812.11.020.931.11

4 结论

由表1可见,采用换算截面法计算组合单向板弹性极限承载力与试验结果吻合较好,有限元模拟结果次之,弯矩-曲率法的计算结果偏大，因此,采用换算截面法计算组合楼板的弹性承载力是可行的,且计算过程简化.而弯矩-曲率法通过编程算出的弯矩-曲率全曲线可反映组合楼板板的非线性性能,对于深入开展组合楼板的研究具有一定的理论意义.