脉冲星信号相干消色散与非相干消色散的比较研究*
黄玉祥,汪 敏,郝龙飞,李志玄,徐永华
(1.中国科学院云南天文台,云南昆明 650011;2.中国科学院大学,北京 100049)
脉冲星是一种具有超高温、超高压、超高密度、超强磁场、超强电场和超强引力场等极端物理条件的天体,一般认为是超新星爆发的产物,典型半径约为10 km,而质量却与太阳相当,核心密度高达1014g/cm3[1]。目前,大多数人认为,脉冲星是高速旋转的磁中子星,其自转轴与磁轴之间有一个夹角,两个磁极各有一个辐射束。脉冲星的辐射几乎占据了整个电磁波谱,包括射电、红外、可见光、紫外、X射线和γ射线等电磁波频段。其辐射具有较高的周期性,辐射周期和自转周期一致,且周期变化率较小。
脉冲星极端的物理特性和辐射的高周期性具有较大的研究意义和应用前景[2]。从科学研究来讲,脉冲星可以用于验证和发展极端条件下的物理学和天文学理论,毫秒脉冲双星的研究已经检验了广义相对论和引力波辐射[3-4];从工程应用来讲,毫秒脉冲星可以用于精确计时和星际导航[1,5]。由于毫秒脉冲星的周期变化率小于10-19,周期噪声极小,周期稳定度比较高,且随时间的增加会持续改善,甚至能超过氢原子钟,多个不同天区的毫秒脉冲星计时观测可以组合成一个平均的脉冲星钟,这可以用于现有原子钟长期稳定性的修正。
为了进行上述研究,就要获得精确的脉冲星脉冲到达时间[1](Time Of Arrival,TOA),由于星际介质的存在,观测设备接收到的脉冲星信号发生色散。为了简化理论,星际介质被看成是低温、低密度等离子体,它对在其中传播的频率为f的电磁波的折射率为

其中,fp为等离子体频率ne取 0.03 cm-3[1]。
对于射电波段观测,接收到的脉冲信号是一维时域上的脉冲轮廓,不同频率的脉冲之间发生色散延迟,频谱起始频率信号相对于其截止频率信号延迟时间[1]为

其中,DM(Dispersion Measure)为传播路径上的星际介质的色散量,色散量单位为为传播路径上的平均电子数密度;D为星际介质的色散常量,MHz2pc-1cm3s;flow和fhigh分别为接收频带的起始频率和截止频率,单位为MHz。
由(2)式可知,一定带宽脉冲星信号的色散延迟会造成时域脉冲的相位移动、幅度降低和脉冲轮廓展宽等色散现象,这限制了到达时间分辨率。因此需要对接收到的脉冲星信号进行消色散并获得精确的到达时间,通过对脉冲到达时间的拟合可以得到脉冲星的相关物理参数,进而研究其自身的辐射机制和其他相关特性。
消色散的宗旨是消除信号频带内的色散效应,目前主要有非相干消色散和相干消色散[1]。非相干消色散是基于时间序列,用滤波器组分通道,按相对于参考通道的延迟时间单个通道进行平移从而消除色散;相干消色散是在频域上利用星际介质的传输函数(chirp函数)实现通带内的消色散,如图1。

图1 消色散算法流程图;上半部分是相干消色散的流程图,下半部分是非相干消色散的流程图Fig.1 Flow chart of coherent de-dispersion algorithm;the above belongs to coherent de-dispersion,the below belongs to incoherent de-dispersion
目前已经有学者在比较两种消色散方法方面进行了一些研究。文[6]在430 MHz处对PSRJ2322+2057进行了观测,获得了相干和非相干消色散后的平均脉冲轮廓,并计算出脉冲到达时间的精度,后者与前者到达时间的均方根误差比值为0.3,如图2。文[7]用数字信号处理(Digital Signal Processing,DSP)算法在327 MHz处比较了这两种方法得到的一些脉冲星信号的积分轮廓,相干消色散后数据的时域序列脉冲幅度和时间分辨率是非相干消色散后数据的10~15倍[7]。国内,中国科学院新疆天文台的脉冲星观测团队利用基于MK5A的VLBI记录系统建立一套带宽为64 MHz的相干消色散系统,得到了一些脉冲星的平均脉冲轮廓,与以前使用的2×128×2.5 MHz多通道非相干消色散系统的结果进行了比较[8],结论是相干消色散优于非相干消色散,但没有进行系统和定量的分析研究。本文旨在用相关系数的方法定量地分析两种方法消色散效果的差别。
1 消色散原理
两种消色散方法基于不同的消色散原理。非相干消色散是基于时域上各个频段的信号相位移动进行的不连续消色散,相干消色散是基于频域乘积的连续消色散,具体描述如下。
1.1 非相干消色散
非相干消色散的过程是首先把观测带宽为BW的时域信号由滤波器组分成若干狭窄通道,然后在时域上把每个通道信号按适当的时延量进行平移,最后将脉冲对齐后的所有通道信号幅度累加得到消色散后的时域信号序列,如图3。非相干消色散的优点是数据量小,计算量少。这种方法的缺点:(1)单个通道内的色散效应没有消除,增大通道的数量可以减少剩余的色散效应,但是由不确定性原理tres∝1/(2×bw)可知,增大通道数量,单个通道信号的时间分辨率会增大,所以要根据需求,适当调整通道数的数值;(2)由于非相干消色散过程是单通道时域序列的平移,该方法会损失信号的相位信息。

图2 脉冲星PSR J2322+2057的脉冲轮廓。实线是相干消色散后的轮廓,虚线是非相干消色散后的轮廓[6]Fig.2 Pulse profile of PSR J2322+2057.Solid line: pulse profile observed by coherent de-dispersion.Dashed line: The same profile, filtered by incoherent dedispersion

图3 消色散原理图[9]。上半部分是非相干消色散的原理,下半部分是相干消色散的原理Fig.3 Schematic diagram of incoherent de-dispersion.The upper part shows the principle of incoherent dedispersion,the lower part shows the Principle of coherent de-dispersion
1.2 相干消色散
星际介质的色散效应相当于移相器的作用,因此接收到的脉冲星信号相当于原始信号加上移相器得到的结果,移相器可以用传递函数H(f)表征,具体表达[1]为

其中,fo为本振频率;f1为中频频率。
由传递函数H(f)可知,原始信号可以通过乘以其复共轭H(-f)进行完全消色散,消除整个观测带宽内的色散效应,如图3,最大的时间分辨率为1/2BW( )。这种消色散方法可用于高精度毫秒脉冲星计时和脉冲星射电辐射过程的研究。
理论上,两种消色散结果的差异主要由各个通道的剩余色散量造成的累加效应,因此分析两种消色散效果可以通过分析各个通道的剩余色散量实现。
对于上边带信号的非相干消色散,由(2)式可知,整个带宽BW内的最大时延:

其中,BW为观测带宽。
单个通道的时间延迟:

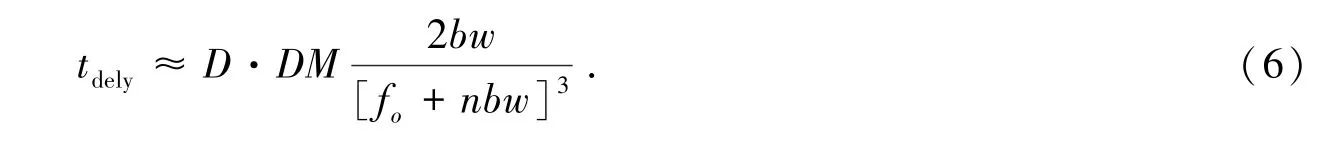
2 脉冲星信号模拟、消色散算法及比较方法实现
本文用MATLAB程序模拟了射电望远镜接收到的脉冲星信号,实现了两种消色散过程和两种消色散方法效果的定量比较过程,具体过程如下。
2.1 原始信号模拟
脉冲星辐射的原始信号很弱,为了提高信噪比,需要长时间的积分。为了简化计算,此处模拟一个周期的基带信号。为了便于比较两种方法的消色散效果,采用短周期0.003 906 25 s,同时为了提高程序的运算效率,采样率(2 Gbps)、采样时长和信号带宽等都取2的幂指数。加色散前的基带信号和加色散后基带信号如图4。色散的基带信号模拟过程如下:

图4 (a)加色散前的基带模拟信号,(b)加色散后的基带模拟信号;信号频谱带宽BW为1 GHz,起始频率fo为1 GHz,色散量DM为40 cm-3·pc,图5也取同样的值Fig.4 The left image is the baseband analog signal before adding dispersion,the right image is the baseband signal after adding dispersion; Signal spectrum bandwidth BW: 1GHz, the starting frequency fo: 1GHz, the Dispersion Measure DM:40cm-3·pc.In the figure.5 those variables also take same value
(1)模拟带宽为BW,起始频率为fo,谱指数为-2.0的基带信号[1]。
(2)把频域的模拟基带信号通过逆傅里叶变换到时域,进行高斯脉冲调制。
(3)把调制后信号再通过傅里叶变换到频域,乘以传输函数H(f)后进行加色散。
(4)把加色散的频域信号再变换到时域,加高斯白噪声成模拟的脉冲星时域信号。
2.2 消色散算法实现
根据模拟长度为N的脉冲星信号数据,利用MATLAB程序实现信号的消色散过程,并实现两种消色散后的序列与加色散前序列的相关过程。
2.2.1 非相干消色散步骤
(1)数据分箱:把模拟的基带数据按顺序平均分箱。
(2)多相位滤波①https://casper.berkeley.edu/wiki/The_Polyphase_Filter_Bank_Technique:对每个箱中的数据进行多相位滤波,数据序列长度减小原始的这可以降低傅里叶变换的频谱泄露[10]。多相位滤波过程为:利用相同长度的sinc函数序列依次乘以每个箱中的数据,把得到的序列按顺序平均分成4段,并逐次对应相加得到原始箱内序列长度数据。
(3)傅里叶变换:对每个箱中的数据进行傅里叶变换。
(4)分通道并平移数据:取参考频率为截止频率fhigh,任意中心频率f的通道按延迟时间平移。由(2)式可知,相对延迟时间为

(5)逆傅里叶变换并求和:把每个箱中数据再进行逆傅里叶变换,然后对箱内的数据求和得到分箱后的数据序列,非相干消色散后信号的二维频谱见图5(a)。

图5 (a)非相干消色散后信号的二维频谱;(b)相干消色散后信号的二维频谱Fig.5 The two-dimensional spectrum of the signal after incoherent de-dispersion,the two-dimensional spectrum of the signal after coherent de-dispersion
2.2.2 相干消色散步骤
基带信号只有一个周期,为了简化运算,将每次处理的数据长度也定为一个周期。具体步骤如下:
(1)直接进行傅里叶变换:把模拟的基带数据进行傅里叶变换,得到频域数据。
(2)频域消色散:把频域数据乘以消色散函数H(-f)得到消色散后的频域数据。
(3)逆傅里叶变换:把消色散后的频域数据进行逆傅里叶变换得到原始序列长度的消色散后的时域数据。
(4)折叠成分箱序列:把消色散后的数据依次折叠成与非相干消色散分箱后序列长度相同的箱,然后把每个箱中的数据累加得到序列,相干消色散后信号的二维频谱见图5(b)。
2.3 消色散效果的定量比较
为了定量分析两种消色散,让两种消色散后的结果与加色散前的数据进行互相关,求它们的互相关系数:

其中,xi属于长度为N的序列X;yi属于长度为N的序列Y。目前普遍认为,相关系数的绝对值在0.3以下代表无直线相关;0.3以上代表直线相关;0.3~0.5代表低度相关;0.5~0.8代表显著相关(中等程度相关);0.8以上代表高度相关;当且仅当其绝对值为1时,代表线性相关。对于研究的信号,表明两个信号完全相同,如相同的脉宽和信噪比。具体步骤为:
(1)把加色散前的模拟数据按上面的方法折叠累加成长度与非相干消色散分箱后序列长度相同的数据序列。
(2)把两种消色散后的数据与上一步的分箱数据进行互相关得到互相关系数。
3 两种消色散的定量比较
首先,研究用上述两组相关系数定量比较两组消色散的效果。然后,估计这两种相关系数小于等于0.01时信号频谱的起始频率。
在信号模拟和消色散过程中,色散量的取值为1~40 cm-3·pc,步长为1 cm-3·pc。信号频谱带宽BW取值为32 MHz、64 MHz、128 MHz、256 MHz、512 MHz和1 GHz,单通道带宽为1 MHz。信号频谱起始频率的取值范围为256 MHz~8 GHz,比较运算耗时和消色散效果,其步长为64 MHz,对于确定两种消色散效果相同时的频谱起始频率,其步长为16 MHz。
3.1 两种消色散结果得到的互相关系数的比较
通过计算得到两种消色散后的数据与加色散前数据的相关系数如图6、图7。首先分析两种消色散结果得到互相关系数随各变量的变化特点。

图6 相干消色散后的数据与加色散前的数据的相关系数;为了便于显示,此处相关系数乘了1 000倍Fig.6 The coherence coefficient of the data after the coherent de-dispersion with the data before the adding dispersion.To facilitate the display,the coherence coefficient is multiplied by 1000
由图6可知,相干消色散得到的相关系数接近于1,这说明,在不考虑离散化运算过程中引入的误差时,相干消色散可以完全恢复原始加色散之前的信号。结合两图可以发现,当BW减小时,相关系数的波动变大,这与(6)式有关;其次,数据处理过程存在频谱泄露,这是由于数据在周期性分箱过程中产生一些截断频点,有限长离散数据的傅里叶变换有频谱泄露,这些效应的影响随着BW的减小而增大。
两种消色散得到的相关系数之差见图7。对于相同的色散量DM,频谱起始频率fo的取值在一定范围内,相关系数之差随着变量fo指数减小,但到某值f1之上,该相关系数之差接近于1且波动逐渐变小,这说明在频谱起始频率fo低于f1时,非相干消色散的效果比相干消色散的差,且两种方法的消色散效果的差距随着fo的增加而缩小。在fo高于f1时,两种方法的消色散效果相同。结合两图可以看出,相同fo随DM变化对应的相关系数的变化曲线随着BW的减小起伏变大,这是数据处理时频谱泄露的误差造成的。相同fo、相同DM对应的相关系数之差随BW的增大而减小,且f1随BW的减小而增大。结合(6)式和图7可知,在不考虑误差范围时,在一定观测频率内,相干消色散效果优于非相干消色散效果,两种方法的消色散效果的差距随观测带宽、观测频率的增加而近似按指数关系减小,随着色散量的增大而近似按幂指数关系增大,同时能够确定,可以找到两种方法消色散效果相同时的观测起始频率。

图7 两种消色散方法得到的相关系数之差Fig.7 The coherence coefficient of the data after the incoherent de-dispersion with the data before the adding dispersion
3.2 两种消色散效果相同对应的通带起始频率
两种消色散效果相同时,这对应于非相干消色散单通道内的时延tdely取某一接近零的常数。非相干消色散过程,若单个通道带宽bw为常数,由(6)式可得

由上式,tdely为常数,有

经过计算,在两种消色散后的数据与加色散前的数据的相关系数小于某一定值条件下,得到频谱起始频率fo如表1,考虑到如上所述数据处理中引入的误差,这个值取0.01。

表1 不同BW、DM对应消色散效果相同时的f o,其单位是MHz,这只是部分数据Table 1 The fo to different BW and DM, which corresponds to the de-dispersion effect,the unit is MHz,This is just part of the data
4 结 论
运用MATLAB程序实现了两种消色散过程的定量比较,并确定了两种消色散方法相同时的频谱起始频率。在实现比较过程中,色散量的取值为1~40 cm-3·pc,步长为1 cm-3·pc;信号频谱带宽BW取值为32 MHz、64 MHz、128 MHz、256 MHz、512 MHz和1 GHz,单通道带宽为1 MHz;信号频谱起始频率的取值范围为256 MHz~8 GHz。对于比较运算耗时和消色散效果,其步长为64 MHz,对于确定两种消色散效果相同时的频谱起始频率,其步长为16 MHz。定量的比较结果说明,在一定的观测频率之内,相干消色散的效果优于非相干消色散,实际观测中可以根据观测要求,参考这些结果,选择消色散方法。最后研究了在不同色散量和不同频谱带宽下,两种消色散技术消色散效果相同时的起始频率,非相干消色散脉冲星观测系统在实际的观测中可以参考这些频率制定观测频段。非相干消色散过程引用了多相位滤波器,一定程度上缓解了傅里叶变换的频谱泄露问题。但是频谱泄露问题依然存在,尤其在低频端和高频端。下一步将扩展色散量的变化范围和变化的单个通道带宽,同时继续改善频谱泄漏问题。
致谢:由衷感谢北京大学李柯伽老师和国家天文台卢吉光博士对脉冲星信号模拟的指导。

