面向代价敏感的多标记不完备数据特征选择算法
黄 琴,钱文彬,王映龙,吴兵龙
(江西农业大学 计算机与信息工程学院,南昌 330045)(江西省高等学校农业信息技术重点实验室,南昌 330045)
1 引 言
由于在许多现实应用领域中,数据特征值的获取通常是需要花费金钱、时间或其他资源作为代价成本,因此,将代价引入到数据挖掘和知识发现领域是显得尤为必要.近年来,代价敏感学习问题作为数据挖掘领域的十大最具挑战性问题之一[1],已受到越来越多研究者的关注,并被广泛应用于医学[2,3]、模式识别[4]、人脸识别[5-8]等各个研究领域.另外,特征选择作为一种有效的数据降维方法[9-12],其目的是通过去除冗余特征,提高数据的质量,加快数据挖掘的速度.由于基于代价敏感的特征选择算法是对特征选择问题的扩展,从而基于代价敏感的特征选择问题也受到了广大研究者的关注.
近年来,基于代价敏感学习的单标记特征选择研究取得了一些有意义的成果.Li等[13]在C4.5算法的基础上提出了基于两种自适应机制的代价敏感决策树算法,一种是选择自适应分割点机制来构建分类器,另一种机制即自适应删除属性机制,在选择节点的过程中删除冗余属性.Zhao等[14]用启发式算法选择结点中的属性,并构造了一种基于加权类分布批量删除属性机制的代价敏感决策树算法.Zhao等[15]通过自适应邻域粗糙集模型和快速回溯算法构造了一种基于自适应邻域粒度的多级置信度的代价敏感特征选择算法.Zhou等[16]提出基于均匀森林的代价敏感特征选择算法,其在构建基础决策树过程中结合特征代价,从而生成低代价的特征子集.Fan等[17]通过测试代价构造自适应邻域模型,从而实现对异构数据的属性约简.Zhao等[18]提出不同粒度下对应不同置信水平相关的数据精度,在覆盖粗糙集模型下设计一种基于置信水平的代价敏感属性选择.Min等[19]提出了一种基于启发式算法的最小化测试代价属性约简方法,并用四种度量方法来评价约简算法的性能指标.Min等[20]提出基于测试代价约束问题的特征选择算法,并用回溯法和启发式算法进行分析.Liu等[21]通过优化F-measures函数,解决不平衡类问题,实现基于测试代价的特征选择的算法.Dai等[22]在有效的索引能力的基础上,提出了一种基于离散粒子群算法在测试代价敏感属性约简中的应用.
上述基于代价敏感的特征选择算法研究主要面向单标记分类问题,但由于多标记高维数据广泛存在于社会生活中[23-25].由此,在代价敏感学习下对多标记高维数据进行特征选择值得进一步研究.同时,在现实生活应用存在大量的连续型、不完备性多标记高维数据.若需对连续型数据进行离散化处理以及缺失数据进行填充处理,将会影响数据计算的精度和增加数据计算的复杂性.
为此,本文提出了一种面向代价敏感的多标记不完备邻域数据特征选择算法,首先,算法在粗糙集模型上通过距离度量公式计算多标记不完备数据下的邻域粒度,并根据多标记不完备数中特征的标准差和特征参数计算出合理的邻域阈值,然后,通过均匀分布和正态分布为每个特征生成特征代价,在特征选择过程中,根据归一化后的正域和特征代价,提出了一种度量特征的重要性计算方法,并在特征核的基础上,根据特征的重要性设计了启发式的特征选择算法;最后,在Mulan数据集上利用五个多标记分类器对考虑代价和不考虑代价的多标记特征选择进行实验比较和结果分析,实验结果表明,本文算法解决了多标记连续型不完备数据在考虑代价情况下的特征选择问题,可选择出代价总和相对较低的特征子集,这为基于代价敏感的多标记不完备高维数据的分析提供了一种可借鉴的方法.
2 相关知识
在粒计算理论中,多标记数据可表示成一个多标记决策表MDT=(U,A∪D,V,f)中,U为对象集{x1,x2,…,xn},也称为论域,A为条件特征集{a1,a2,…,am},D为多标记决策特征{l1,l2,…,lk},且A∩D=Ø.V为全特征集的值域,其中V=∪Va,a∈A∪D,Va表示特征a的值域,f是U×(A∪D)→V的信息函数.
定义1.当多标记决策表中存在缺失值时,记缺失值为“*”,即至少存在a∈A,x∈U,使得f(x,a)=*,此时数据称为多标记不完备决策表IMDT=(U,A∪D,V,f).
定义2.给定多标记不完备决策表IMDT=(U,A∪D,V,f),对于任意特征子集B⊆A,定义特征子集B的容差关系T(B):
T(B)={(xi,xj)|(xi,xj)∈U×U,∀at∈B⟹f(xi,at)=f(xj,at)∨f(xi,at)=*∨f(xj,at)=*}
定义3.对于N维的实数空间Ω中,Δ=RN×RN→R,∀xi,xj∈RN,则称Δ为RN上的一个度量,(Ω,Δ)为度量空间,Δ(xi,xj)为距离函数,表示元xi和xj之间的距离:
当p=1时,称为曼哈顿距离.当p=2时,称为欧氏距离.
3 问题描述
由于基于粗糙集的粒计算方法主要是处理名义型或符号型数据,但在现实应用领域中多标记数据的数值类型往往较复杂,当需处理数值型数据,须先对数据进行离散化,而对连续数据离散化将可能导致重要的信息丢失,从而影响分类算法的分类性能,为此需对连续型数值的多标记不完备数据开展特征选择的研究.
定义4.[26]对于多标记不完备邻域决策表IMDT=(U,A∪D,V,f),若有特征子集B⊆A,特征子集B上的邻域粒度为
δB(xi)={x|x∈U,Δ(x,xi)≤δ}
其中,δ为邻域的阈值大小.
下面以表1为例,若以曼哈顿距离作为邻域度量标准,根据定义3计算各对象之间的邻域粒度.
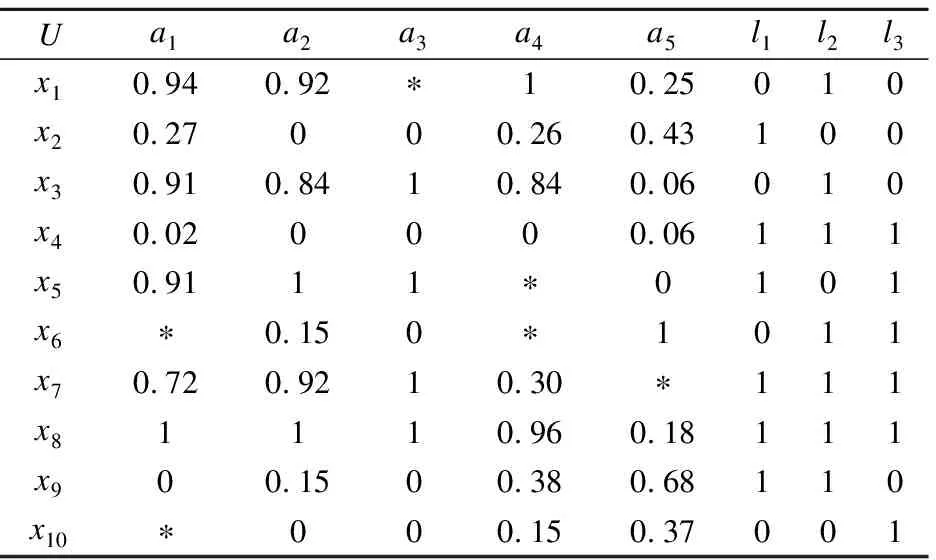
表1 多标记不完备邻域决策表Table 1 Incomplete neighborhood multi-label decision table
利用曼哈顿距离度量公式,若特征a1、a2、a3、a4、a5的邻域阈值分别为0.21、0.22、0.24、0.18、0.15.根据定义4计算包含所有特征的每个对象的邻域粒度:
δA(x1)={x1,x8},δA(x2)={x2,x10},
δA(x3)={x3,x5,x8},δA(x4)={x4},
δA(x5)={x3,x5,x7,x8},δA(x6)={x6},
δA(x7)={x5,x7},δA(x8)={x1,x3,x5,x8},
δA(x9)={x9},δA(x10)={x2,x10}.
同理,可计算每个特征下每个对象的邻域粒度.
定义5.在多标记不完备邻域决策表IMDT=(U,A∪D,V,f)中,假设U中包含N个对象空间,对象xi对应的标记集合用yi来表示,N个对象实例所对应的向量用y=(y1,y2,…,yn)来表示.对象xi中所对应的第k个标记值用lk来表示,若lk=1,则表示yi集合中所对应的存在第lk个标记.
以表1为例,根据定义5可计算每个xi对象所对应的标记集合yi为:
y1={l2},y2={l1},y3={l2},y4={l1,l2,l3},y5={l1,l3},y6={l2,l3},y7={l1,l2,l3},y8={l1,l2,l3},y9={l1,l2},y10={l3}.
定义6.在多标记不完备邻域决策表IMDT=(U,A∪D,V,f)中,对于∀lk∈D,分别计算存在标记决策lk所对应的对象集合Dk:
Dk={[x]lk|x∈U}
以表1为例,根据定义6可计算存在标记决策lk所对应的对象集合Dk:
D1={x2,x4,x5,x7,x8,x9}
D2={x1,x3,x4,x6,x7,x8,x9}
D3={x4,x5,x6,x7,x8,x10}
定义7.在多标记不完备邻域决策表IMDT=(U,A∪D,V,f)中,将拥有类别标记lk的对象集合用Dk表示,将对象xi所具有的标记集合用yi来表示.给定B⊆C,多标记不完备邻域粗糙集的上下近似集为:
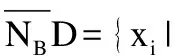
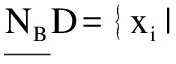
定义8.在多标记不完备邻域决策表IMDT=(U,A∪D,V,f),有特征子集B⊆A,特征子集B上的正域为:
以表1为例,根据定义7和定义8可计算特征集A下的正域.具体的计算过程如下:
由于对象x1所对应的标记是l1,所以只需判断δA(x1)⊆D2是否成立,若成立,则对象x1在正域范围.因为δA(x1)={x1,x8},δA(x1)⊆D2,所以x1∈POSA(D).同理可得x4∈POSA(D),x6∈POSA(D), x9∈POSA(D).由此可知,POSA(D)={x1,x4,x6,x9}.
定义9.在多标记不完备邻域决策表IMDT=(U,A∪D,V,f)中,多标记不完备邻域决策表基于正区域核的定义为:
Core(A)={a|a∈A,POSA-{a}(D)≠POSA(D)}
以表1为例,根据定义9可计算出特征集A下的核,由计算可知:POSA-{a5}(D)≠POSA(D);由此可知,特征a5为核即Core(A)={a5}.
定义10.在多标记不完备邻域决策表IMDT=(U,A∪D,V,f),对于特征子集B⊆A,特征子集B的特征依赖度为:
定义11.在多标记不完备邻域决策表IMDT=(U,A∪D,V,f),特征子集B⊆A,若特征子集B是多标记不完备邻域决策表的一个特征选择结果,则B需满足:
1)γB(D)=γA(D)
2)∀at∈B,γB-{at}(D)<γB(D)
条件1)确保了特征子集B和全特征集A下的正域对象相同,条件2)确保了特征子集B中没有冗余特征.
当前,由于在许多现实应用领域中,数据特征值的获取通常是需要花费金钱、时间或其他资源作为代价成本,为此,基于代价敏感下多标记不完备邻域数据的特征选择问题值得进一步研究.
定义12.当多标记不完备邻域决策表中的特征需要考虑代价时,则称该决策表为基于代价敏感的多标记不完备邻域决策表,其定义为:CIMDT=(U,A∪D,V,f,c),c:A→R+∪{0}是独立测试代价函数,其中代价为非负数.
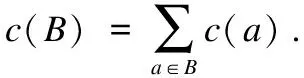
以表1为例,可给出多标记不完备邻域决策表的测试代价向量,如表2所示.

表2 测试代价向量表Table 2 Vector of test cost table
性质1.基于代价敏感的多标记不完备邻域决策表CIMDT=(U,A∪D,V,f,c),特征子集B⊆A,对于任意特征at,ai∈A-B,则基于测试代价的特征at的重要度为:
SIGcost(at,B,D)=POSB∪{at}(D)*-CostB∪{at}(D)*
为了方便性质1中对测试代价的特征at的重要度计算,先需对基于特征子集的正域个数和测试代价分别进行归一化处理:
POSB∪{at}(D)*=
CostB∪{at}(D)*=
其中max(|POSB∪{ai}(D)|)、min(|POSB∪{ai}(D)|)分别为特征子集B中加入任意特征后的最大和最小正域个数,max(CostB∪{ai}(D))、min(CostB∪{ai}(D))分别为特征子集B中加入任意特征后所对应的最大代价和最小代价.
由定义9可知,特征a5为核,因此,先将a5加入到特征子集B中,结合表1和表2 中的数据计算出特征a1、a2、a3、a4基于测试代价的特征重要度分别为:
SIGcost(a1,B,D)=0.7;
SIGcost(a2,B,D)=0.85;
SIGcost(a3,B,D)=0.25;
SIGcost(a4,B,D)=-0.2;
由上面计算可知,特征a2的特征重要度最大,由此将a2加入到特征子集B中,通过计算可知,此时POSB(D)=POSA(D),则特征子集B={a2,a5},结合表2中给出的代价可知,此时特征子集B所需花费的测试代价是$18,而整个特征全集下的测试代价为$52.
4 特征选择算法
根据上述分析可知,针对代价敏感的多标记不完备邻域决策表的特征选择算法,首先,采用均匀分布和正态分布两种分布函数分别为每个特征生成特征代价,根据邻域的阈值计算基于代价敏感的多标记不完备邻域决策表中每个对象的邻域粒度,在此基础上,得到基于代价敏感的多标记不完备邻域决策表的正域对象集合.然后,根据基于测试代价特征的重要度计算公式计算除特征核之外的每个条件特征的重要度,每次将特征重要度最大的特征加入当前的特征子集中并更新特征子集中正域对象集,直到特征子集下的正域对象集合等于全特征集下的正域对象集,由此设计了一种面向基于代价敏感多标记不完备邻域决策表的特征选择算法,算法描述如下:
输入:基于代价敏感的多标记不完备邻域决策表
输出:特征子集Red.
Begin:
Step1.初始化Red←Ø;
Step2.对于∀xi∈U,计算在特征集A下每个对象的邻域粒度δA(xi);
Step3.对于∀lk∈D,分别计算每个标记lk下的对象集合Dk;
Step4.若δA(xi)⊆Dk,则将对象xi存入正域POSA(D)←POSA(D)∪{xi};
Step5.对于∀aj∈A,分别计算去除每个特征之后对象的正域集合POSA-{aj}(D),若POSA-{aj}(D)≠POSA(D),则将特征aj存入Red, 算法转至Step7;
Step6.对于∀aj∈A-Red,执行操作:
Step6.1.计算条件特征集Red∪aj下每个对象的邻域粒度δRed∪aj(xi);
Step6.2.对于多标记∀lk∈D且lk=1,若δRed∪aj(xi)⊆Dk,则POSRed∪aj(D)←POSRed∪aj(D)∪{xi};
Step6.3.若at=argmax{SIGCos t(aj,c,D)},则Red←Red∪{at},即计算加入条件特征aj的重要度SIGCos t(aj,c,D), 选择重要度最大的条件特征at存入Red;
Step7.若POSRed(D)≠POSA(D),则算法转至Step6,否则执行Step8;
Step8.输出特征子集Red,算法结束;
End
算法的时间复杂度分析:
算法Step1初始化一个变量存放特征选择后的特征子集,其时间复杂度为O(1);算法Step2在整个条件特征集下通过对象之间的比较计算得到每个对象的邻域粒度,其时间复杂度为O(|C‖U|2);算法Step3分别计算每个标记决策下的对象集合,其时间复杂度为O(|C‖D|);算法Step4计算多标记不完备决策表的正域对象集,其时间复杂度为O(|U|2+|U‖D|);算法Step5计算特征核的时间复杂度为O(|C|);算法Step6对加入的新特征后的特征子集正域集合更新,实现对基于代价敏感的多标记不完备数据的特征选择,最坏的时间复杂度为O(|C‖U|);算法Step7判断约简后的特征子集下正域与整个论域的正域是否一致,最坏的时间复杂度为O(|U|).综述分析,本文算法的时间复杂度为O(|C‖U|2).
5 实验与结果分析
5.1 数据集及实验设置
为了验证本文中所提出的基于代价敏感多标记不完备数据特征选择算法的有效性,从Mulan数据集中选取了yeast、emotions、scenes、birds 4个真实数据集,并分别用均匀分布(Uniform Distribution)和正态分布(Normal Distribution)两种分布函数(Cumulative Distribution Function,记为CDF)分别为这4个数据集生成测试代价,在对基于测试代价的多标记数据集进行实验测试和分析,均匀分布的均匀数取值在0~100之间,正态分布以100为期望值,以30为标准差,4个数据集的相关信息和不同分布函数下4个数据集所对应的测试总代价分别如表3、表4所示.
本次实验的硬件配置为CPU为Inter(R)Core(TM)i5-4590s(3.0GHz),内存8.0GB.设计算法所使用的编程语言为Python和Java,使用的开发工具分别是记事本和Eclipse 4.7.
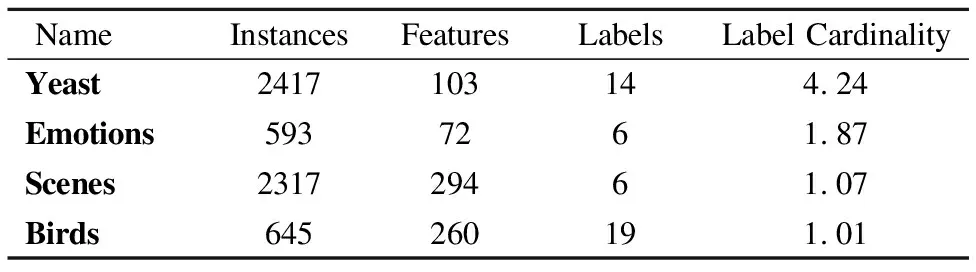
表3 多标记数据集表Table 3 Multi-label datasets table

表4 数据集总测试代价表Table 4 Cost of multi-label datasets table
5.2 性能指标

1)代价约简率是考虑特征代价的特征子集B的代价占全特征集A总代价的比率:
2)平均精度是指在标记预测序列中,排在相关标记之前的标记仍是相关标记的比率:

3)汉明损失是指预测出的标记与实际标记的平均差异值:
其中Δ为Yi、Zi两个集合之间的对称差.
4)覆盖率是指所有对象实际包含的所有标记所需最大的排序距离:
5)1错误率是指预测出的标记排序最靠前的标记不在实际对象中的比率:

6)排序损失是指预测出的标记中实际不包含的标记比实际包含的标记排序高的比率:
其中平均分类精度越大越好,汉明损失、覆盖率、1错误率、排序损失越小越好.
5.3 实验分析与比较
由于文中的多标记数据特征选择算法是基于代价敏感的,所以在进行实验测试之前,需先用均匀分布和正态分布两种分布函数分别为以上4个数据集的特征生成测试代价,通过比较基于不同分布函数的特征代价来评价测试代价对多标记数据特征选择算法的影响.同时,文中研究的是不完备数据,因此,需用均匀函数对以上4个数据集进行5%的数据缺失处理.在实验测试和分析的过程中,为了避免实验结果的均匀性,采用10倍交叉验证法对每个数据集的实验结果进行验证.在实验过程中,首先利用曼哈顿距离度量方法计算邻域粒度,同时,在特征核的基础上,对每个数据集进行特征选择.然后比较考虑代价和不考虑代价特征选择的结果,通过5种多标记分类器(RAkEL、DMLkNN、IBLR_ML、BRkNN、MLkNN)验证了算法的性能,且通过多标记的五大评价性能指标评估和对比分类器的分类性能.
5.3.1λ特征参数的确定
对于基于代价敏感的多标记不完备邻域决策表,特征选择的结果与特征代价直接相关,因此,在实验过程中,对基于均匀分布和正态分布生成的两种特征代价获得的特征选择结果进行对比,同时,由于邻域参数的选择直接关系到特征选择的结果和分类器的分类性能.为此,在曼哈顿距离度量方法中,邻域参数的计算方式为δ=stdai/λ,其中stdai通过本文算法进行特征选择之后的每个特征的标准差,λ的取值直接关系到邻域参数δ的值[27].通过实验分析发现,λ的取值范围从1.0到2.0的特征选择结果所对应的分类性能较好,为此,为了详细分析λ值对特征选择结果和分类器的分类性能影响,在实验过程中将λ值每次变化0.1进行实验分析和结果对比.
下面将分析不同分布函数随着λ变化对特征选择结果以及代价的影响,详细分析基于不同分布函数生成的测试代价在曼哈顿距离度量标准下λ(在图中用Lambda表示λ)变化对于特征选择的个数和特征子集总代价影响.图中UDASBC、NDASBC分别表示在均匀分布和正态分布下考虑特征代价的特征选择个数,UDAS、NDAS分别表示在均匀分布和正态分布下不考虑特征代价的特征选择个数,UDCPBC、NDCPBC分别表示在均匀分布和正态分布下的代价约简率,即考虑特征代价的特征子集代价占总代价的百分比(由于两种分布函数生成的代价不同,因此两种分布函数通过代价百分比分析),UDCP、NDCP分别表示在均匀分布和正态分布下不考虑特征代价的特征子集代价占总代价的百分比.具体实验结果如图1所示.

图1 4个数据集在两种分布函数下特征选择的个数和代价百分比随λ值的变化情况Fig.1 Variation of the number of feature selection and the value of the cost percentage for the four datasets under the two distribution functions with λ
由图1可知,对于4个数据集来说,随着λ变化,特征选择个数和代价百分比都呈下降趋势.考虑测试代价比不考虑测试代价的特征选择效果更优,例如对于图1(e)和图1(f)中的scenes数据集,当不考虑测试代价时 ,特征选择个数最小为39,当考虑测试代价时,均匀分布和正态分布下特征个数最小分别为17、22,分别占不考虑测试代价特征选择结果的43%、56%;同时,考虑测试代价的代价百分比不考虑测试代价的代价百分比相对更小,当考虑测试代价时,均匀分布和正态分布下代价百分比最小分别为0.40%、3.60%,而不考虑测试代价时,均匀分布和正态分布下代价百分比最小分别为13.26%、13.19%,代价分别减少了12.86%、9.59%.另外,当代价百分比最小时,在均匀分布下代价百分比相差最为显著的是图1(a)中的yeast和图1(e)中的scenes数据集,最小代价百分比相差大于11%,在正态分布下代价百分比相差较明显的是图1(b)中yeast、图1(d)中的emotions和图1(f)中的scenes数据集,最小代价百分比相差大于9%.由此可知,对于yeast和scenes数据集来说,考虑代价与不考虑代价的代价百分比的差在均匀分布下比正态分布下大.当λ取值为1.9或2.0时,特征选择个数和代价百分比最小.
综上可知,考虑代价的特征选择效果优于不考虑代价的特征选择效果,考虑特征代价的代价百分比小于不考虑特征代价的百分比.
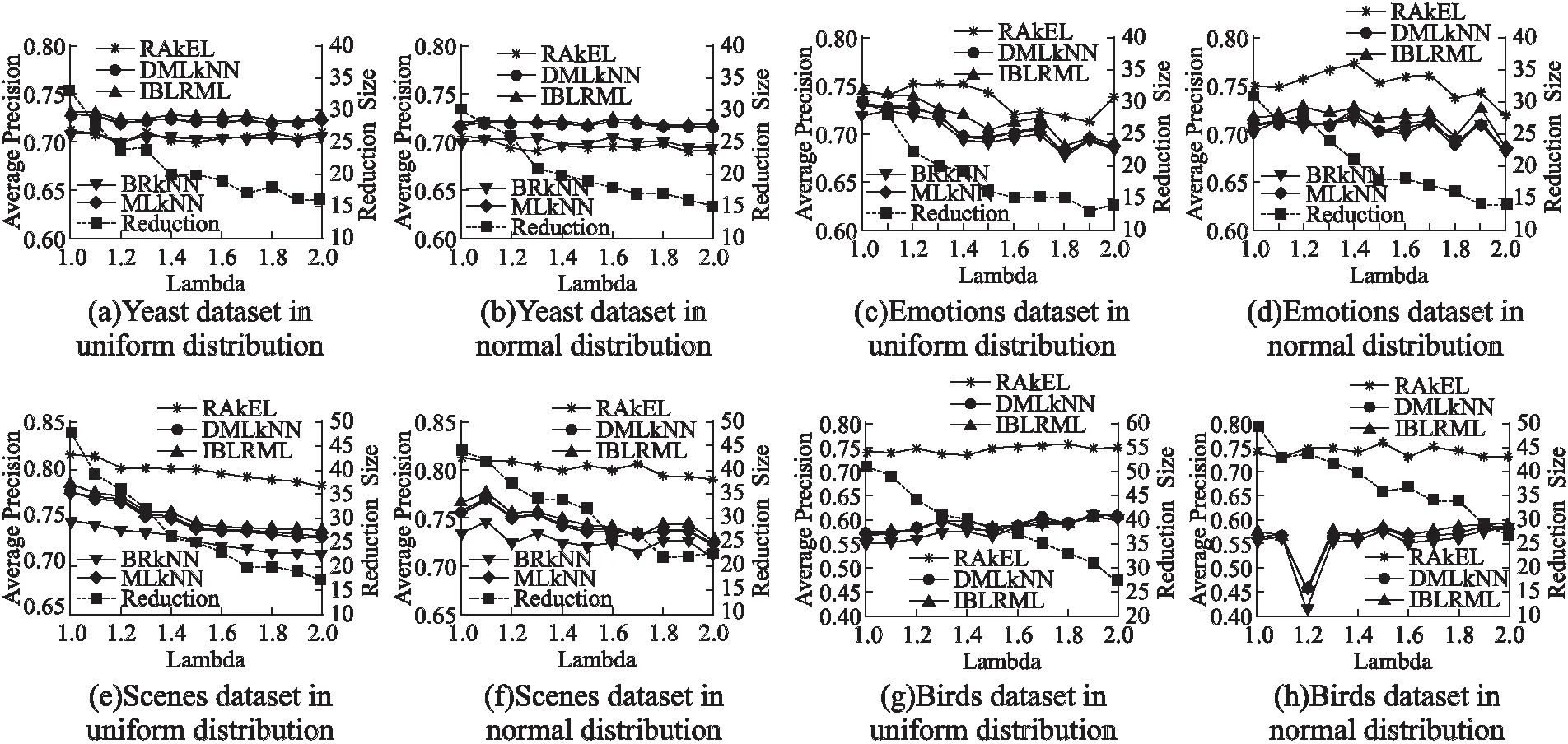
图2 4个数据集在两种分布函数下平均精度随λ值的变化情况Fig.2 Variation of the average precision with the values of the four datasets under the two distribution functions with λ
由图2可知,当λ取值在1.0-2.0之间,在两种分布函数下,特征选择的个数都呈下降趋势.在均匀分布下,对于图2(a)中的yeast、图2(e)中的scenes和图2(g)中的birds数据集来说,随λ取值的变化,5个分类器的平均分类精度的变化相对不明显,当λ=2.0时,3个数据集的特征选择结果和分类性能较优;对于图2(c)中的emotions数据集来说,平均精度随λ取值的变化无明显规律,当λ=1.2时,5个分类器的平均精度较优.在正态分布下,随λ取值的变化,图2(d)中的emotions数据集的平均精度的变化显著,图2(b)yeast和图2(f)scenes数据集的平均精度变化较平缓,图2(h)中的birds数据集在λ=1.2,除RAKEL分类器外,其他4个分类器的平均精度显著下降,参数λ在变化到1.2之后的平均精度变化相对平缓.对于yeast、emotions、scenes、birds数据集来说,当λ取值分别为2.0、1.4、1.9、2.0时对应数据集的特征选择结果和分类性能较优.
综上可知,每个数据集在5个多标记分类器上最优的平均分类精度所对应的λ参数不尽相同,参数λ的取值也影响特征选择的结果.
5.3.2 实验结果和讨论
为进一步验证本文算法的有效性,下面将在4个Mulan数据集上利用两种分布函数为特征生成测试代价,通过5个多标记性能指标在曼哈顿距离度量下进行实验对比和分析,实验结果如表5-表8所示,其中,λ为特征参数,AS为特征选择的个数,PC为代价百分比,AP为分类器的平均分类精度,HL为汉明损失,Coverage为覆盖率 、OE为1错误率、RL为排序损失,带有↑的性能指标表示值越大越好,↓性能能指标表示值越小越好.另外,表中分别给出5个分类器的平均精度最优时,对应的λ参数、特征子集的大小、特征子集的代价百分比和其他4个分类性能指标的值.
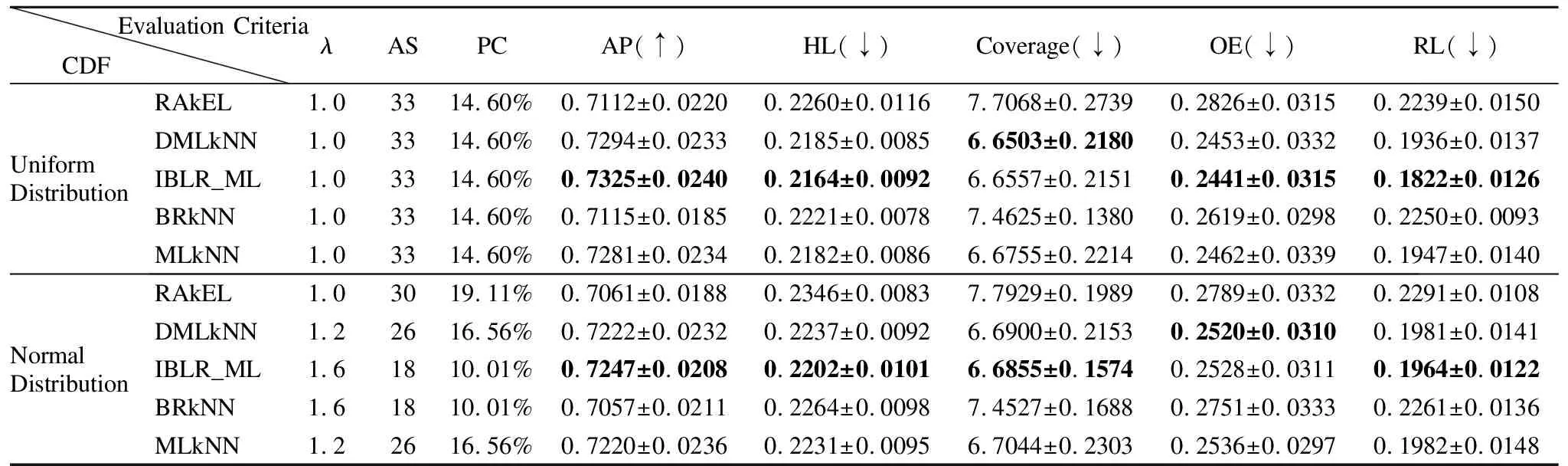
表5 两种分布函数下Yeast数据集的分类性能指标比较Table 5 Comparison of classification performance of yeast dataset under two distribution functions
从表5-表8的实验结果可知,当分类器的平均分类精度最优时,均匀分布与正态分布相比,4个数据集在均匀分布下,5个分类器的分类性能相对较优.在均匀分布下,yeast、emotions、scenes和birds这4个数据集所对应的5个分类器的平均特征个数分别是33、27、43、31,分别占原有特征的32.0%、27.2%、14.6%、11.9%;在正态分布下,这4个数据集所对应的平均特征个数分别是23、20、42、30,分别占原有特征的22.9%、27.8%、14.29%、11.5%.其中,在yeast数据集中,使用均匀分布比正态分布下的特征选择算法效果提高了9.1%,而其他4个数据集特征选择的差异并不明显.同时,在均匀分布下,yeast、emotions、scenes和birds这4个数据集所对应的五个分类器的特征选择结果的代价百分比分别是14.60%、33.52%、3.62%、9.94%;在正态分布下,这4个数据集所对应的特征选择结果的代价百分比分别是14.45%、20.39%、8.89%、9.22%,由此可知,emotions和scenes数据集在不同分布函数下代价百分比的差异较大.由实验结果可知,本文的基于代价敏感的特征选择算法降低了多标记学习的计算时间和空间消耗,且有效地节省了成本代价.同时,由表5-表8的实验结果对比发现,选择的特征子集直接影响到多标记分类器的分类性能.在上述4个数据集中,由于特征子集的结果不同,导致5种分类器的分类性能也不相同.例如,在均匀分布下,birds数据集在RAkEL分类器下的平均分类精度为75.60%,而在IBLR_ML分类器下的平均分类精度为60.79%,两个分类器的性能差异超过14%;在正态分布下,birds数据集在RAkEL分类器下的平均分类精度为76.26%,而在BRkNN分类器下的平均分类精度为58.20 %,两个分类器的性能差异超过18%.由实验结果可知,对于yeast数据集来说,IBLR_ML分类器的分类性能优于其他4个分类器的分类性能;对于emtions、scenes和birds数据集来说,RAkEL分类器分类性能较其他4个分类器的分类性能更优.
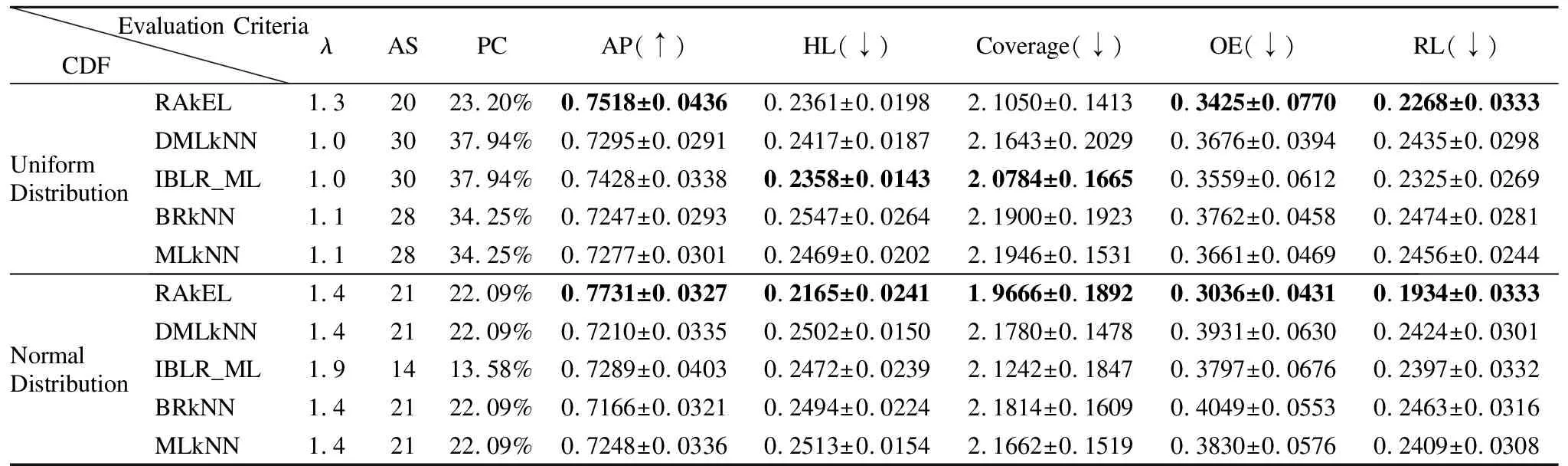
表6 两种分布函数下Emotions数据集的分类性能指标比较Table 6 Comparison of classification performance of Emotions dataset under two distribution functions

表7 两种分布函数下Scenes数据集的分类性能指标比较Table 7 Comparison of classification performance of Scenes dataset under two distribution functions
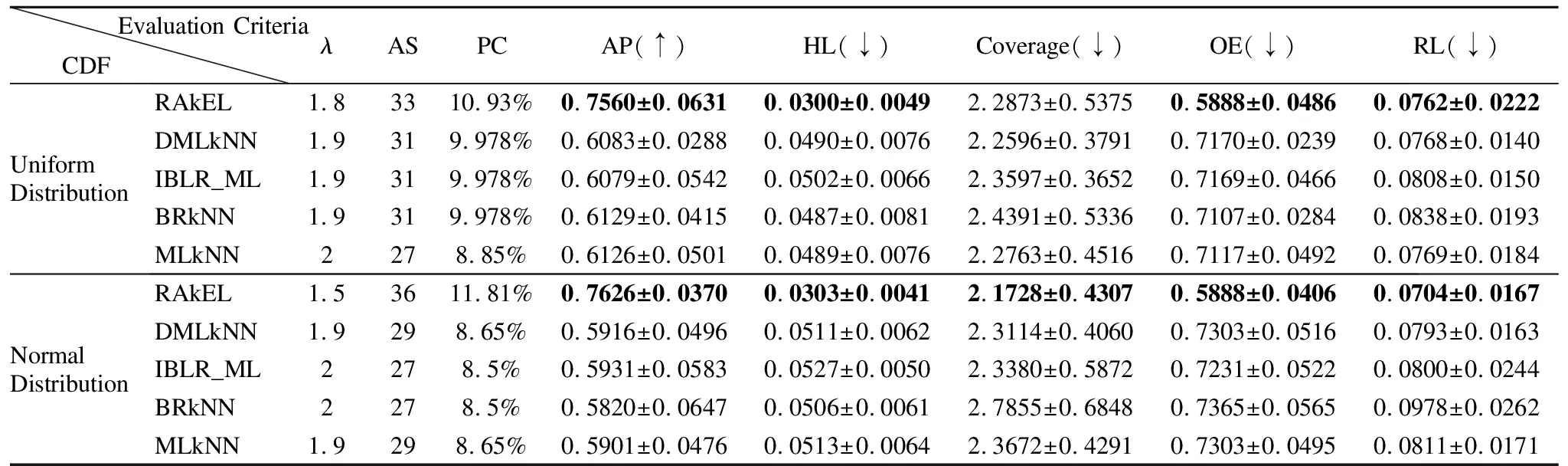
表8 两种分布函数下Birds数据集的分类性能指标比较Table 8 Comparison of classification performance of Birds dataset under two distribution functions
综上所述,本文算法特征选择的结果和分类性能与特征代价、λ参数和分类器的选择相关.通过表5-表8的实验结果和分析可知,本文算法解决了对代价敏感下多标记不完备邻域数据的特征选择问题,有效剔除了数据中的冗余特征,降低特征的代价成本,提高了分类器的分类性能.
6 结束语
针对多标记高维数据中的连续值、缺失值以及特征的测试代价等问题,从代价敏感学习的视角,提出了一种面向不完备特征邻域决策表的多标记特征选择算法,算法利用均匀分布和正态分布两种分布函数分别为每个数据特征生成代价,分析特征代价对特征选择的影响;算法可直接对不完备连续型数据进行处理,无需对缺失数据进行填充及对连续数据进行离散化.算法通过距离度量对不完备特征邻域决策表进行邻域粒化,并根据正域计算出核特征,在此基础上,采用启发式搜索策略对多标记不完备决策表进行特征选择,在实验结果中通过对考虑特征代价和不考虑特征代价的数据集的特征选择结果进行实验和分析验证了算法的有效性.由于现实生活中除需要考虑测试代价之外,还需考虑误分类代价,下一步工作将研究基于测试代价和误分类代价的多标记数据特征选择问题.

