面向分类型矩阵数据的无监督孤立点检测算法

吴晓林，曹付元

1)山西大学计算机与信息技术学院, 山西太原030006；2)山西大学计算智能与中文信息处理教育部重点实验室, 山西太原 030006

数据挖掘通常分为关联规则发现、类别判定、类别描述和孤立点检测[1]4种类型．孤立点检测作为数据挖掘的一个重要任务，被广泛用于信用卡防欺诈、 网络监测、 电子商务、 故障检测、 恶劣天气预报和卫生系统监测[2]等方面．HAWKINS[3]给出了孤立点的本质性定义，认为孤立点是在数据集中与众不同的对象，可能这些数据并非随机偏差，而是由完全不同的机制产生的． 孤立点检测可以形式化地描述为：给定一个包含n个对象的数据集和期望的孤立点数目p， 根据算法找到明显不同的、异常的前p个对象，这p个对象就是所要找的孤立点．

现有的孤立点检测算法主要有基于距离的方法[1, 4]、基于密度的方法[5]和基于偏离的方法[6]等．这些算法的输入都是一个包含n个对象的数据集，且每个对象由一个矢量描述．但是，在许多实际应用中，数据集中一个对象通常由多个矢量描述．表1列举了某超市顾客的部分购物信息．

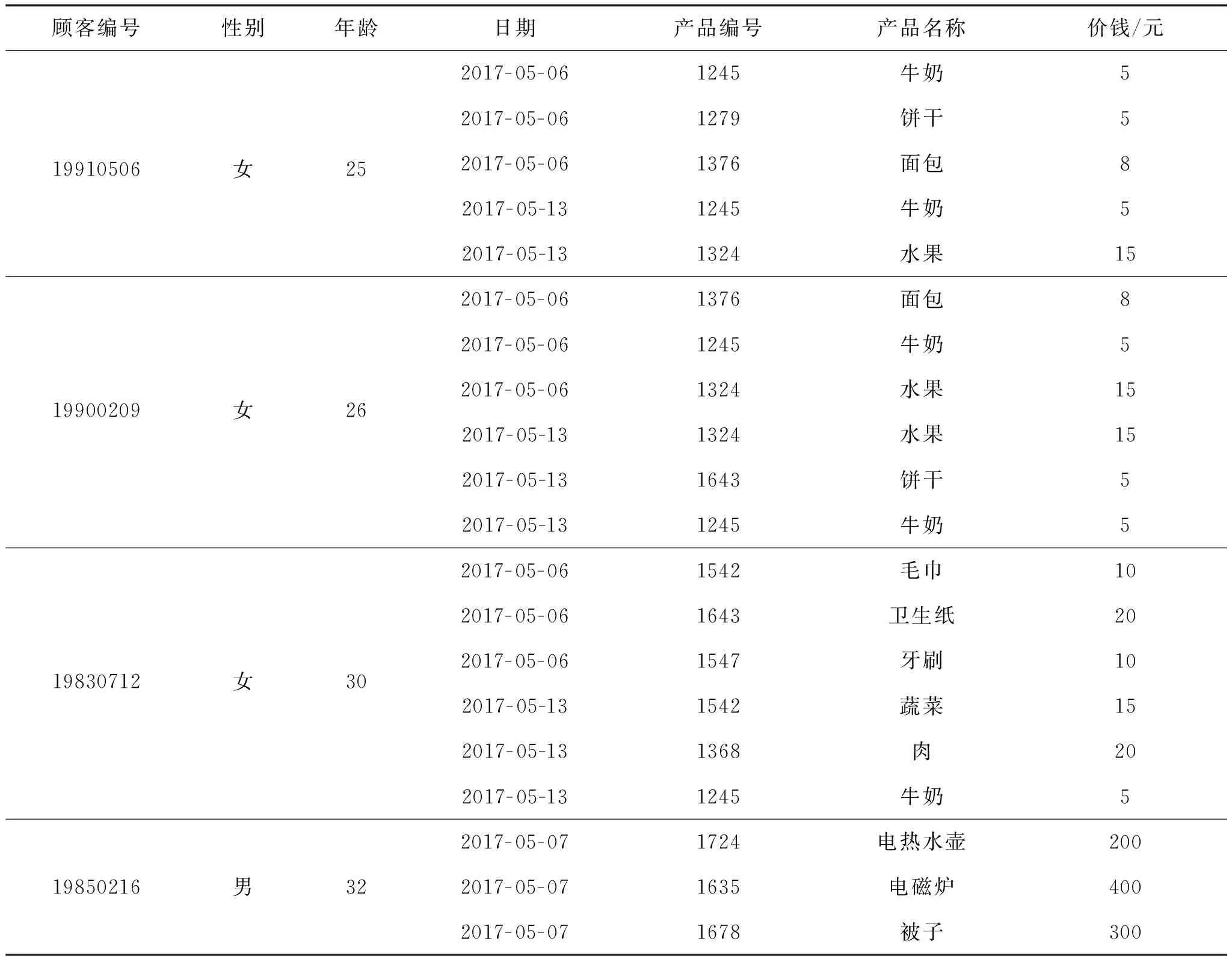
表1 超市顾客的部分购物信息Table 1 Shopping information of some supermarket users

表1由两部分组成，顾客编号、性别和年龄是顾客的基本信息，日期、产品编号、产品名称和价钱是顾客的购买信息．观察表1，发现其中的数据具有以下特征：

1)相关性．顾客基本信息和购买信息两部分数据可能存在一定的相关性，表现在不同性别或年龄的顾客可能有不同的购物偏好．例如，表1中25岁和26岁的女性顾客购买倾向相似，她们仅购买了食品，而32岁的男性顾客则购买了家用电器和日用品．

2)一对多．表1中每个顾客均对应不止1条记录．例如，顾客19910506有5条购买记录，而顾客19830712有6条购买记录．

3)混合性．描述一个对象的属性既有分类型又有数值型．比如产品编号是分类型属性，价钱是数值型属性．

4)演化性．某些属性值会随着时间的推移而改变．例如，顾客19830712在某天买了生活用品，但在另一天只买了食品，顾客购买动态的变化隐含了顾客行为的变化．

从表1中所列的顾客购物日期、产品编号、产品名称和价钱可见，每个顾客可能购买多个商品，并且每种商品可能同时被多个用户购买．此外，商品也可以由一个顾客多次购买．通过交易记录可以找到不同顾客的购买特征．如表1中前3名顾客都买了食品，但最后一位顾客没有买食品，他购买了其他顾客没有购买的3件商品，说明最后一位顾客与前3位用户的购物倾向差异最大．因此，可认为编号为19850216的顾客在表1中是一个孤立点．表1所示的数据集结构被广泛用于银行、保险、电信和医疗等领域．

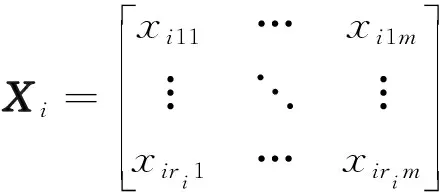
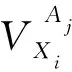
若使用现有的孤立点检测算法来处理矩阵数据，最直接的方法是压缩和转换数据，转换成用一个矢量表示一个对象．对于数值型变量，通常用均值来表示，而对于分类型变量，则选择用频率高的属性值来代表．但是，在数据压缩和转换的过程中通常会有大量信息被丢失，因此该方法不足以完全反映用户的真实行为．为更好地找出矩阵数据中的孤立点，需要发展新的孤立点检测算法．

孤立点检测是通过一种有效的方法挖掘给定数据集中与多数对象不同的少数对象，可将其视为基于对象之间定义的不相似性(相似性)度量的问题．在实际应用中，矩阵数据集大部分以混合属性来描述，对于数值型描述的矩阵数据，可通过Hausdorff距离[7]或其他衍生距离公式来度量对象之间的相似性；而分类型矩阵数据之间由于缺乏固有的几何特性，很难定义矩阵对象之间的相似性．因此，如何对分类型矩阵数据进行孤立点检测是一个非常具有挑战性的问题．

针对分类型矩阵数据，本研究通过定义一种矩阵对象本身的内聚度和该对象与其他矩阵对象间的耦合度，给出了矩阵对象的孤立因子计算公式，提出一种面向分类型矩阵数据的孤立点检测算法，并通过真实数据集上的实验结果验证了算法的有效性.

1 孤立点检测相关工作

20世纪60年代后期，孤立点检测首次被提出，并一直受到人们的关注．数据挖掘和机器学习的不断发展，推动了孤立点检测的研究，且进一步产生了许多新算法．根据数据标签的可用性，可将孤立点检测方法分为监督检测、半监督检测和无监督检测3大类．原则上，监督检测和半监督检测都需要训练集，而无监督检测不需要任何训练集．监督检测包括正类和负类标签的实例，而半监督检测训练集中通常只包括正类标签的实例．现阶段关于监督的孤立点检测研究相对较少，下面仅讨论无监督和半监督检测的相关工作．

无监督孤立点检测方法不需要任何带标签的数据，且假设数据集中的大多数对象是正类．根据数据类型可分为数值型孤立点检测和分类型孤立点检测．针对数值型数据，BREUNIG[5]提出了一种局部异常因子(local outlier factor, LOF)算法，主要通过比较对象p与其邻域对象的密度比值来判断该对象是否为孤立点，该比值越接近1，表明p与其邻域对象密度越接近，p可能和邻域同属一簇；该比值越小，说明p的密度大于其邻域点密度越多，p为密集点；该比值越大，说明p的密度小于其邻域点密度越多，总之，两者差值越大，p越可能是异常点．此外，LOF算法易受到计算第k个近邻距离的影响．JIANG 等[8]基于DÜNTSCH等给出的信息熵模型提出了一种无监督孤立点检测算法．在一个给定的信息系统中，首先计算相对基数，通过对比此基数，将所有对象分为两类：属于少数类的对象和属于多数类的对象．然后，计算每个对象的相对熵，属于少数群体且相对熵很高的对象更可能成为一个孤立点．针对分类型数据，WU 等[9]提出了一种基于信息理论的分类型无监督孤立点检测算法，基于熵和全相关系数提出了全熵的概念，给出了一个孤立点的新定义，并建立了孤立点检测的优化模型．基于该模型，定义了对象的孤立因子的函数公式，提出ITB-SS和ITB-SP两种孤立点检测方法．PANG等[10]介绍了一种新的框架SelectVC，它通过迭代学习选择值耦合将值选择和孤立点得分组合去发现高维分类型数据中的孤立点，通过实例POP(partial outlierness propagation)验证了SelectVC的性能．

半监督孤立点检测方法在训练阶段不需要负类标签的实例，只需要在训练数据集中构建正类实例的模型，将测试数据集中与正类模型不同的实例识别为孤立点．针对数值型数据，DANESHPAZHZHOUH等[11]提出了一种在给定少数正类实例标签信息情况下的半监督孤立点检测算法，该算法分为两个阶段：首先，从正类和未标记的实例中提取一个负类候选集；然后，在候选集中采用基于信息熵的算法来检测前N个孤立点．通过第1阶段的计算，数据集的大小显著减少，降低了算法的时间复杂度．TANG等[12]提出了一种基于局部核密度估计的局部孤立点检测算法，通过考虑k个最近邻、反向最近邻和共享最近邻来估计局部核密度，计算每个对象的相对密度来检测孤立点．针对分类型数据，NOTO等[13]提出了一个处理分类型数据的半监督孤立点检测算法，利用训练集中的正实例构建一组特征模型，然后将与这些模型不匹配的实例识别为孤立点．LENCO等[14]介绍了一种处理分类型数据的半监督孤立点检测算法，给定一组训练实例(都属于正常类)，分析特征之间的关系，建立一个表示正常实例特征的模型，然后使用一组基于分类属性距离的技术来区分正常类数据和异常类数据．综上可知，尽管现阶段孤立点检测算法有很多，但是处理的数据集中每个对象都是由1条记录描述，对于矩阵数据集尚无有效处理算法，为此，本研究提出一种针对分类型矩阵数据的孤立点检测算法.

2 一种分类型矩阵数据无监督孤立点检测算法

通常用孤立因子定义一个对象的孤立程度. 在软件工程中，通常以耦合度和内聚度为标准来衡量模块的独立程度．耦合度是软件系统结构中模块之间紧密程度的度量．模块之间的连接越紧密，耦合性越强，模块的独立性越差．内聚度是衡量模块功能强弱的指标，如果模块中的元素紧密相关，则模块的内聚度就高．本研究通过矩阵对象与其他对象之间的耦合程度，以及其自身的内聚程度来确定一个对象的孤立因子．

2.1 耦合度

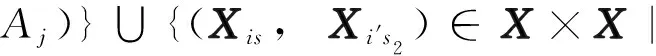
定义1给定一个矩阵数据集X， 对于任意Aj∈A， IND({Aj})是由Aj确定的不可区分关系，X/IND({Aj})={B1,B2,…,Bk}记为由IND({Aj})导出的一个划分． IND({Aj})在X上的信息熵定义为

(1)

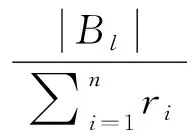
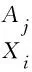
(2)

其中，Xis在属性Aj上的相对信息熵REAj(Xis)，且

(3)

对于任意Aj∈A，Xis∈X， 当删除By时，若信息熵大幅降低，则可认为By中的元素在X中出现的频率很低；反之，若信息熵减幅很小或增加，则认为By中的元素在X中出现的频率很高．因此，相对信息熵REAj(Xis)能够反映Xis的孤立程度．相对信息熵REAj(Xis)越高，则Xis越孤立．

若X/IND({Aj})={By,X-By}， 则MEAj(Xis,By)=0， 相应地， REAj(Xis)=1． 因此，对于任意的Xis∈X, 有0≤REAj(Xis)≤1．

给定一个矩阵数据集X， 为找到X中的孤立点，首先可根据一个给定的标准将X中的所有对象分成两类：属于X中的少数群体的对象和属于X中多数群体的对象．此标准可定义为：

(4)

若RC(Xis,By)>0， 则Xis属于多数类；反之，若RC(Xis,By)≤0， 则Xis属于少数类．

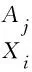
ODAj(Xis)= REAj(Xis)×

(5)

少数类中对象与多数类中的对象相比，少数类中对象更可能为孤立点．如果RC(Xis,By)≤0， 则Xis属于少数类；相应地，相对信息熵REAj(Xis)越大，孤立度也越大，因此，Xis可能越孤立．

基于给定Xis∈X在属性Aj上的孤立度，下面给出矩阵对象耦合度的定义．

定义5给定一个矩阵数据集X， 对于任意一个对象Xi， 耦合度定义为

Cou(Xi)=

(6)

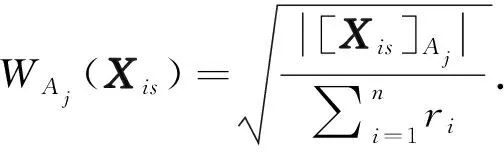
2.2 内聚度

考虑对象的耦合度后，可进一步定义矩阵对象的内聚度．

(7)

由于0≤MEAj(Xi)≤lbri， 所以归一化为HEAj(Xi)=MEAj(Xi)/lbri．

可见，一个矩阵对象内聚度可定义为

(8)

2.3 孤立因子

在定义了一个矩阵对象的耦合度和内聚度的基础上，该矩阵对象的孤立因子可定义为：

定义7给定一个矩阵对象Xi， 其孤立因子为

OF(Xi)= (1-Cou(Xi))×

(1+Coh(Xi))

(9)

在矩阵数据中检测孤立点，既要考虑矩阵对象的耦合度，也要考虑内聚度，但对象的耦合度占主要因素，因此，要减少内聚度所占的权重，将内聚度加1．矩阵对象的孤立因子越大，孤立度越大．

2.4 例子

给定一个矩阵数据集X={X1,X2,X3,X4,X5}，A={A1,A2}， 见表2．

表2 一个矩阵数据集Table 2 A matrix-object data set

矩阵对象X1的孤立因子计算过程如下：

1)根据定义2，每个属性上的信息熵分别为

ME({A1})=1.927 5

ME({A2})=1.828 9

2)根据定义3，对象X1中，每个X1s所在的等价类删除时的信息熵为

MEA1(X11)=1.685 5

MEA2(X11)=MEA2(X13)=1.657 7

MEA1(X12)=MEA1(X13)=1.488 5

MEA2(X12)=1.352 0

由此可得相对熵

REA1(X11)=0.125 5

REA2(X11)=REA2(X13)=0.093 6

REA1(X12)=REA1(X13)=0.227 7

REA2(X12 )=0.260 7

3)根据定义4，相对标准为

RC([X11]A1)= 5.500 0

RC([X11]A2)=RC([X13]A2)=6.750 0

RC([X12]A1)=RC([X13]A1)=1.750 0

RC([X12]A2)=1.750 0

4)根据定义5，可得

ODA1(X11)=0.043 6

ODA2(X11)=ODA2(X13)=0.029 2

ODA1(X12)=ODA1(X13 )=0.102 8

ODA2(X12 )=0.117 7

5)根据定义6，可得对象X1的耦合度为

Cou(Xi)=0.570 2

6)根据定义7，可得对象X1的内聚度为

Coh(Xi)=0.579 2

7)根据定义8可得对象X1的孤立因子为

OF(X1 )=0.678 8

同理可得，OF(X2 )=0.820 3、OF(X3 )= 0.820 3、OF(X4 )= 0.728 1和OF(X5 )=1.265 9． 可见，X5的孤立因子最大，即孤立度最大．

3.5 算法实现

图1给出了分类型矩阵数据孤立点检测算法(outlier detection algorithm for matrix-object data, ODAMD)的伪代码．

图1 ODAMD算法伪代码Fig.1 The pseudocode of ODAMD algorithm

3 实 验

为验证本算法的有效性，在3个真实数据集上进行了实验，分别是从Data website(http://www.datatang.com)下载的Market basket data； 从UCI网站(http://archive.ics.uci.edu/ml)下载的Microsoft web data； 从MovieLens 网站(http://grouplens.org/datasets/movielens/)上下载的MovieLens data．首先，对数据集进行预处理并给出评价指标；然后，将提出的方法与3种孤立点检测算法进行比较．

3.1 数据预处理

在大多数情况下，真实数据集的分布是无序的．实验中3个真实数据集中的孤立点也没有明确标注信息．为解决此问题，首先要对给定的数据集进行预处理．通过可视化技术，可以删除一些点，以获得相对清晰的数据分布，也可以清楚地看到一些对象是孤立的，因此，能够得到一个带有标记信息的数据集.最后，在新的数据集上运行本算法并评估算法的性能．为获得给定分类型数据集的分布，使用多维尺度变换(multi-dimensional scaling, MDS)技术[15]来可视化数据集，该技术的主要方法是将距离公式获得的n阶距离方阵传递给Matlab的mdscale函数，获得n个点的坐标，然后可视化这n点来反映数据的分布．以下是3个真实数据集的预处理过程．

3.1.1 Market basket data

从Data website下载的Market basket data记录了1 001个用户交易信息，每个用户有4个属性(用户ID、时间、产品名称和产品ID)．本研究只考虑用户ID和产品ID，而不考虑时间和产品名称，因为所有用户在属性时间上都具有相同的值，而产品名称的值与产品ID是一一对应的． 此外，Market basket data的突出特点是每个用户都有7条交易记录． 因此， 每个用户是一个典型的分类型矩阵对象．

图2 预处理后的Market basket数据集分布Fig.2 Distribution of preprocessed Market basket data

Market basket data的预处理过程为：首先，通过MDS技术对数据集进行可视化；然后，在坐标系中选择位于x<-0.2，y<0.2或x>0.5内的对象，形成一个包含319个矩阵对象的新数据集．新数据集的分布如图2．其中，“+”和“+×”表示新生成的数据集，“+”表示的对象可认为孤立点．从图2可见，经过统计分析可得，“+”表示的对象属性值出现频率很低．

3.1.2 Microsoft web data

从UCI下载的Microsoft web data是通过对网站www.microsoft.com上的日志进行采样和处理而创建的．它记录了32 711名匿名用户在1998年2月访问该网站时的信息，每个人可多次访问网站．每个用户都有2个属性，包括用户ID和统一资源定位符(uniform resource locator, URL)． 因此， 每个用户都是一个分类型矩阵对象．

预处理过程为：在初始数据可视化后，选择横坐标值位于x<0或x>0.68的点，形成589个对象的新矩阵数据集，然后可视化新矩阵数据集，结果如图3．

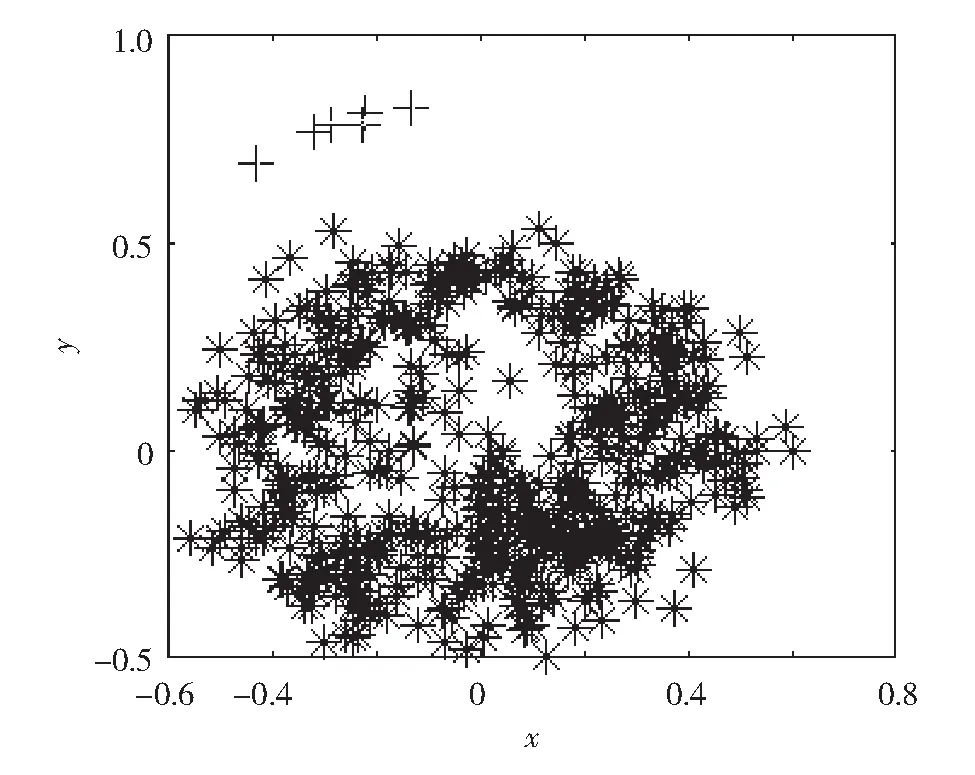
图3 预处理后的Microsoft web数据集分布Fig.3 Distribution of preprocessed Microsoft web data

从图3可见，数据集由两部分组成，其中由符号“+”表示的对象可被视为新数据集中的孤立点．

3.1.3 MovieLens data

实验使用了MovieLens数据集，它包含6 040个用户对3 900部电影的1 000 209条评分，由4个属性表示，分别为UserID(用户编号)、MovieID(电影编号)、Rating(评分)和Timestamp(时间)．因为属性Timestamp在每个记录具有不同的值，因此不考虑该属性．

预处理过程为：在初始数据集可视化后，选择坐标系中-0.10.6范围内的对象作为新的数据集．新数据的可视化结果如图4．

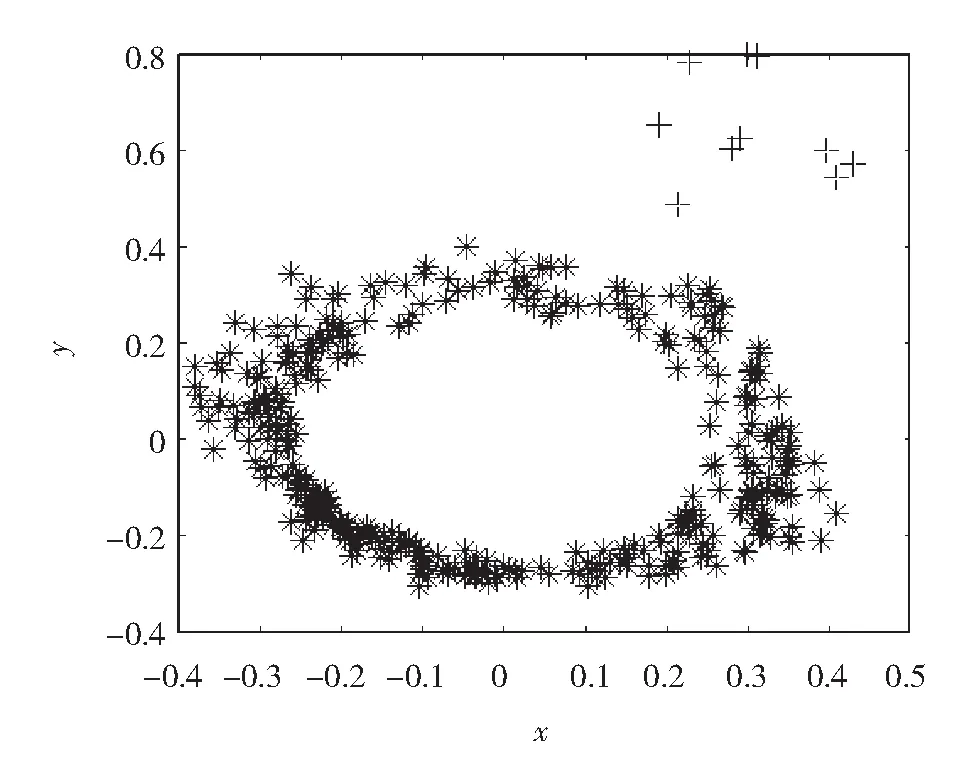
图4 预处理后的MovieLens数据集分布Fig.4 Distribution of preprocessed MovieLens data

从图4可见，数据集是由一个大类和一些散点组成的，这些由符号“+”描绘的散点可看作是孤立点．

3.1.4 数据预处理结果

预处理后的数据集如表3．其中，p为孤立点的数目．

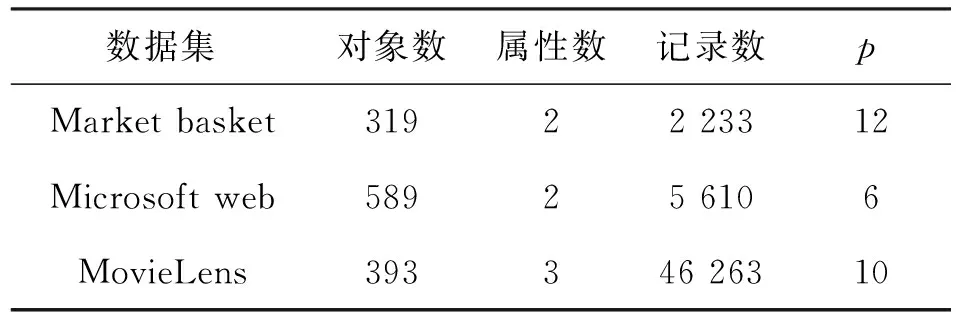
表3 预处理后的数据集Table 3 Preprocessed data set

3.2 评价指标

为验证孤立点检测算法的性能，使用精确度(Precision)、召回率(Recall)、F-度量(F-measure)[16]进行评价．这3个评价指标的计算公式分别为

(10)

(11)

(12)

其中，TruePositive为检索到准确的孤立点数目；FalsePositive为检索到不是孤立点的数目；FalseNegative为未检索到的孤立点数目.

精确度是检索出的相关文档数与检索出的文档总数的比率，衡量的是检索系统的查准率；召回率是检索出的相关文档数与文档库中所有相关文档数的比率，衡量的是检索系统的查全率；F-度量是这两个指标的综合评价指标，用来反映总体指标．Precision和Recall的值在[0, 1]内，且越接近1，实验结果越好．

3.3 实验结果

为验证本研究提出的孤立点检测算法的有效性，将ODAMD算法与基于共同近邻(common-neighbor-besed, CNB)算法[17]、LOF和基于信息熵(information entropy-beased, IE-based)算法[8]进行比较．由于现阶段没有方法可以处理分类型矩阵数据集，所以先将矩阵数据集进行了压缩，每个矩阵对象用频率最高的属性值来表示，新生成的数据集中，一个对象只有一条记录，然后在新生成的数据集中进行实验．

真实数据集上的实验结果如表4至表6．从表4至表6可见，提出的孤立点检测算法效率很高，但其他方法并不理想. 因为数据集进行压缩时，会导致许多信息的丢失．

表4 不同算法在真实数据集中的精确度Table 4 Precision of different algorithms in real data sets

表5 不同算法在真实数据集中的召回率Table 5 Recall of different algorithms in real data sets

表6 不同算法在真实数据集中的F-度量Table 6 F-measure of different algorithms in real data sets

为进一步验证提出的算法的扩展性，在真实数据集上设置不同的孤立点数目，检测新算法与比较算法的精确度，实验结果如图5至图7.

图5 不同算法在Market basket数据集上不同孤立点数目的精确度Fig.5 (Color online) Precision of different algorithms for different number of outliers in Market basket data

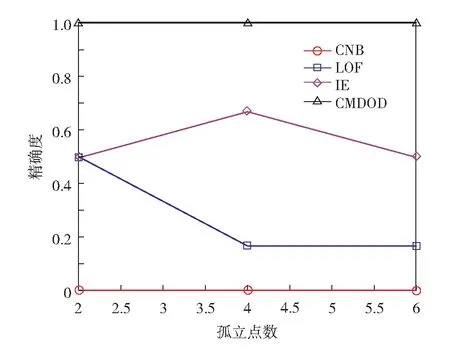
图6 不同算法在Microsoft web数据集上不同孤立点数目下的精确度Fig.6 (Color online) Precision of different algorithms for different number of outliers in Microsoft web

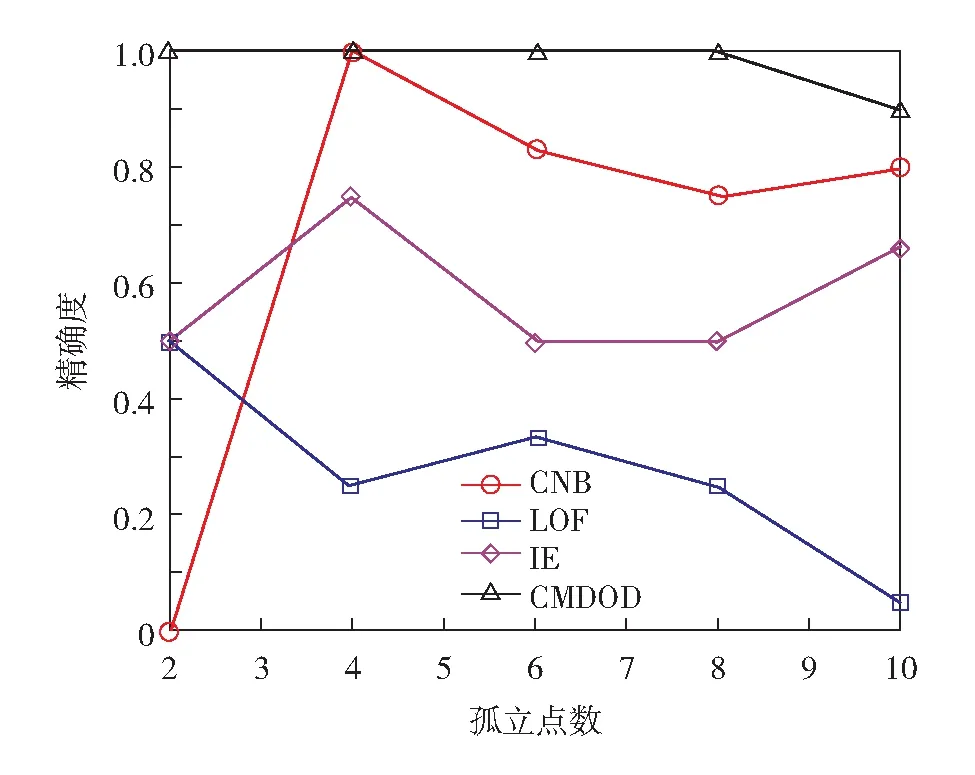
图7 不同算法在MovieLens数据集上不同孤立点数目下的精确度Fig.7 (Color online) Precision of different algorithms for different number of outliers in MovieLens data

从图5至图7可见，随着孤立点数目的增加，提出算法的准确率比较高且比较稳定，而3个比较算法精确度偏低，且不稳定.比如CNB算法在数据集中存在4个孤立点时，精确度为1，但在其他孤立点数目的情况下，精确度比较低．

结 语

针对在实际应用中广泛存在的分类型矩阵数据，提出一种新的孤立点检测算法ODAMD．首先，定义了一个矩阵对象与其他对象间的耦合度；然后，基于信息熵定义了一个矩阵对象自身的内聚度，在此基础上给出了分类型矩阵对象的孤立因子计算方法．在真实数据集上的实验结果证明，本研究提出的孤立点检测算法行之有效．