基于二部图的快速聚类算法

聂飞平，王成龙，王 榕

西北工业大学计算机学院，西北工业大学光学影像分析与学习中心，陕西西安 710072

聚类是模式识别和统计机器学习等领域最基本的问题之一．大多数聚类算法基于欧式几何描述数据相似性[1-2]，但难以有效刻画非凸数据集分布．基于拉普拉斯矩阵特征分解的谱聚类算法由于可有效利用数据的图和流形信息，可学习更多类型的数据结构分布，在非凸分布等复杂数据分布上与其他算法(如k-means)相比经常会有更好的表现．一般来说，谱聚类算法可以分为3个步骤：① 相似图构建；② 谱分析；③ 应用k-means等离散化程序获得最终聚类结果．谱聚类的实现非常简单，可以通过标准的线性代数方法求解[3]．近几十年来，人们提出了各种各样的谱聚类算法[3]，如ratio cut算法[4]和normalized cut算法[5]将数据转换为基于相似性的加权无向图，然后通过图优化算法进行求解．NG 等[6]将数据投影到一个低维空间，在这些空间中有很多方法可以将它们分离，比如使用k-means算法．然而谱聚类由于涉及大图构建，特征分解等高计算复杂度操作[4-6]，难以直接应用于大规模聚类．

1 目标函数设计

谱聚类算法用无向加权图表示数据关系，通过对图中的边进行分割，将数据图划分为不同的连通分量完成对数据的聚类．因此，在数据图中表示数据点间关系的边的连接对于类簇结构发现至关重要．对于大规模的高维数据，稀疏性和冗余往往同时存在．冗余数据带来不必要的连接，这增加了计算复杂度．然而，考虑到数据的稀疏性和流形假设，少量的采样数据点往往就足以覆盖整个点云，本研究将这些采样数据点简称为锚点．利用原始数据和锚点的耦合结构，可以快速学习到聚类结果．LIU等[7]在半监督学习中首先应用了这种选择锚点的策略，并基于二部图给出了一种快速构图方法．CAI等[8]将通过k-means方法选择锚点的策略看作是对原始数据的稀疏编码，求解稀疏编码矩阵的过程其实是求解一个有稀疏约束的线性回归问题的过程．

本算法致力于学习一个数据-锚点二部图(其中边的权重表示对应的数据与锚点的相似度)，并基于二部图完成快速聚类．令zij表示第i个数据点与第j个锚点之间的相似度，即对应数据点和锚点的连接关系．在理想的类簇结构中，不同类的锚点和数据之间没有连接，属于同一类的锚点和数据点相互连接，且连接概率越大，相似度分配越高．

令X=[x1,x2, …,xn]T∈Rn×d表示数据矩阵，U=[u1,u2, …,um]T∈Rm×d表示锚点，则锚点uj可以以zij的概率连接到xi． 数据点和锚点之间的距离越近，连接的概率就越大．本算法将使用一种自适应近邻构图方法[9]来构造初始相似矩阵．其中，第i个点的近邻分配可以被描述为

(1)

其中， 加粗的1表示矢量1;α为正则化参数．如果没有正则化项， 则式(1)会很容易得到平凡解，即最接近xi的锚点被分配为xi近邻点的概率为1，而其他所有点被分配为xi的近邻点的概率都将为0．α的值可以通过文献[9]算法求解．然后，代入α的值求解问题(1)，从而获得数据和锚点的关系矩阵Z∈Rn×m．

进一步，可得到二部图的相似矩阵为

(2)

其中，S∈R(n+m) ×(n+m)．

通常情况下，式(1)无法在任意α值的情况下实现理想的近邻分配，所有的数据点和锚点会被连接在一起，成为一个全连通图．在这种情况下，经典谱聚类算法[8]会通过求解式(3)来解决此问题．

(3)

s.t.zTi1=1, 0≤zij≤1,

(4)

简言之，本研究提出的算法通过自适应近邻策略来构造二部图， 并且对这个图的拉普拉斯矩阵施加了秩约束，从而可以直接从图的划分上得到清晰的类簇结构．下面将对该目标函数的优化进行理论推导，同时分析该算法的计算复杂度．

2 理论分析

2.1 算法优化

如前所述，聚类问题被描述为一个具有离散约束的目标函数，但由于离散约束难以求解，本研究先对离散约束进行松弛，再采用交替优化的方法对目标函数进行优化．

根据 Ky Fan 定理[15]，可得

(5)

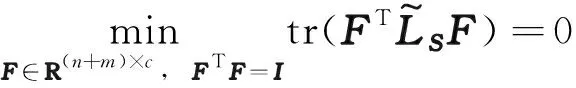
s.t.zTi1=1, 0≤zij≤1,

F∈R(n+m)×c,FTF=I

(6)

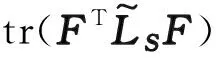
同式(4)相比，式(6)更容易求解．本研究使用交替优化的算法求解式(6)．

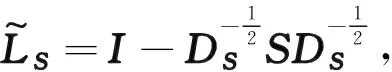
(7)

将F和DS分别写为如式(8)和式(9)的块矩阵形式

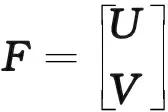
(8)

(9)

其中，U∈Rn×c；V∈Rm×c；DSu∈Rn×n；DSu∈Rm×m．

根据式(2)，式(7)可进一步写为

(10)

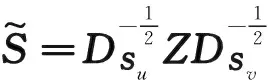
当F固定时，式(6)变型为

s.t.zTi1=1, 0≤zij≤1

(11)

根据归一化拉普拉斯矩阵的性质， 可得

(12)

其中，sij为S的元素.根据式(2)可将式(12)写为

(13)

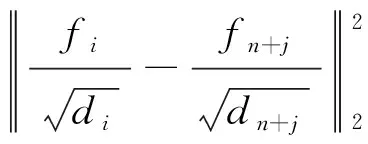
s.t.zTi1=1, 0≤zij≤1

(14)

需要注意的是，式(14)对于不同的i是独立的，所以对于每个i可分别求解式(15)．

s.t.zTi1=1, 0≤zij≤1

(15)

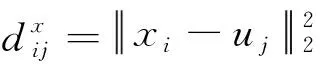
(16)

式(16)可根据文献[9]求得闭式解．

优化完毕．

本研究提出的FCBG算法，在每次迭代中只需要更新连接数据点和该数据点最相似的k个锚点间的边的权重，再在一个n×m的矩阵上进行奇异值分解(singular value decomposition, SVD)，因此更新Z和F的计算复杂度非常低(只计算一个非常稀疏的矩阵的前c个特征向量)．所以，FCBG算法可有效处理大规模数据．

在实际运行时，为加速程序，需在迭代时调整λ． 将λ的初始值设为α， 然后在每次迭代中，若S的连接分量小于c， 就将λ增加一倍；反之，若比c大就将λ减小为λ/2．

FCBG算法的详细流程见图1．

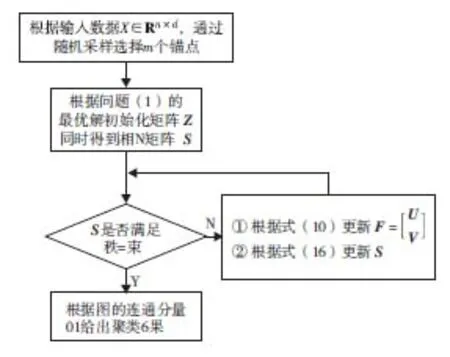
图1 FCBG算法流程图 Fig.1 The flow chart of FCBG algorithm

2.2 时间复杂度分析

给定X∈Rn×d， FCBG算法由4个阶段组成：

1) 锚点生成．通过随机选择生成m个锚点的时间复杂度可忽略不计．

2) 初始化矩阵Z∈Rn×m． 这需要根据问题(1)的最优解从m个锚点中找到k个最近邻点，并且计算相似性．该步骤的计算复杂度为O(nmd+nmlog(m))．

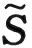
4) 直接根据二部图的连通性得到聚类结果．该步骤时间复杂度为O(n+m+nk)．

考虑到m远小于n， 且t通常都非常小，FCBG算法的时间复杂度与样本数目n呈线性关系

3 实验结果与分析

为说明FCBG算法的有效性，将该算法与其他大规模谱聚类算法在真实数据集上进行对比．本实验通过随机采样为FCBG算法选择锚点，当然也可以基于这一框架，使用其他选择代表性锚点的方法，如随机投影树方法等．

3.1 实验设计

我们将原始的谱聚类(spectral clustering，SC)作为基准算法．

对比算法采用文献[8]提出了一种用于大规模聚类问题的基于地标点的谱聚类算法．该算法选择p个代表性数据点作为地标，并将原始数据点表示为这些地标的线性组合．然后利用基于地标的表示来有效地计算数据相似矩阵的谱嵌入．基于不同的代表点选择策略，该算法可分为使用随机采样的大规模谱聚类(large spectral clustering based on random selection，LSC-R)算法和使用k-means的大规模谱聚类(large spectral clustering based onk-means selection，LSC-k)算法．LSC-R算法时间复杂度为O(nmd+m3+m2n+nmdt1)， LSC-k算法的时间复杂度为O(nmdt+nmd+m3+m2n+nmdt1)． 其中，t为选择锚点时k-means的迭代次数；m为代表点数量；n为样本点个数；d为数据维度；t1为离散化步骤时k-means的迭代次数．

实验中所有代码的运行环境都是Matlab R2018a，硬件系统配置为3.30 GHz，i5-4590 CPU，16 Gbyte 运行内存，Windows 10．

3.1.1 评价指标

为评估聚类结果，采用聚类准确率(ACC)、归一化互信息熵(normalized mutual information, NMI)这两种被广泛使用的聚类性能指标．

ACC指标可以发现聚类结果和真实类标签之间的一对一关系，且测量每个聚类所包含的来自对应类别的数据点的多少，其计算式为

(17)

其中，ri为xi聚类结果给出的类标签；li为真实的类标签；n为样本数量；δ(x,y)是德尔塔函数， 当x=y时，函数值为1，否则，函数值为0； map(ri)是置换映射函数，可将每个聚类标签映射到数据集的真实对应类标签．

NMI指标用于确定聚类的质量．给定一个聚类结果，则

(18)

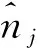
3.1.2 实验数据集

将FCBG算法在基准数据集Palm25、 Clave-Vectors和Aloi上分别进行实验．Palm25数据集是掌纹数据集，包含了100类物体的总共2 000张灰度图，每张样本包含图片像素值对应的256个维度．ClaveVectors数据集由16维二进制特征组成，表示在 4/4 拍的音乐中鼓点敲击的记录，用于打击乐的分类．Aloi数据集是由1 000个小物体组成的彩色图像集合．每个样本由128个特征组成．这3个基准数据集的统计信息见表1．

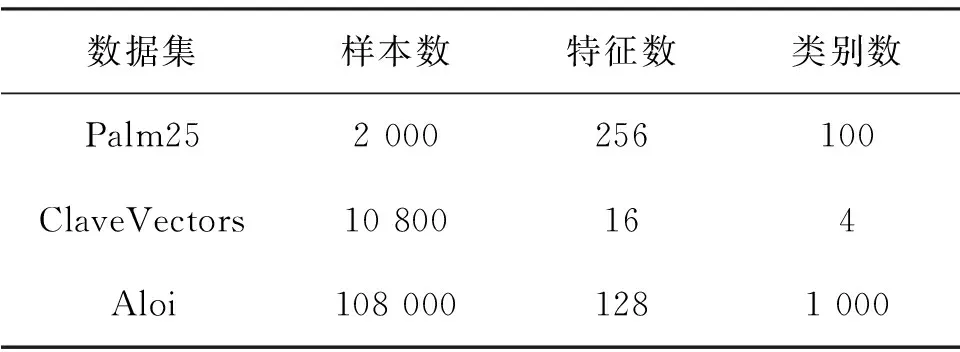
表1 三个基准数据集统计信息Table 1 The statistics of three benchmark datasets

3.2 实验结果

考虑到每种数据集样本数规模不一致，且不同的锚点数量对聚类结果存在影响(需要注意的是，锚点数量必须大于类别数，否则算法不满足秩约束)，选择使算法聚类结果最好的锚点数，即为ClaveVectors、Palm25、和Aloi数据集设置的锚点数量m分别为16、128和1 024．在实验时，每种算法都进行了20次测试并取平均值，表2和表3分别记录了FCBG算法与对比算法在真实数据集上的聚类准确度、NMI的均值．表4记录了所有算法在数据集上运行20次时所需要的平均时间．

在表2至表4中将参与对比的算法最好的结果进行标记．结果可见，就聚类准确率和NMI而言，FCBG 算法在3个数据集上均保持了显著的优势，优于对比算法的结果．

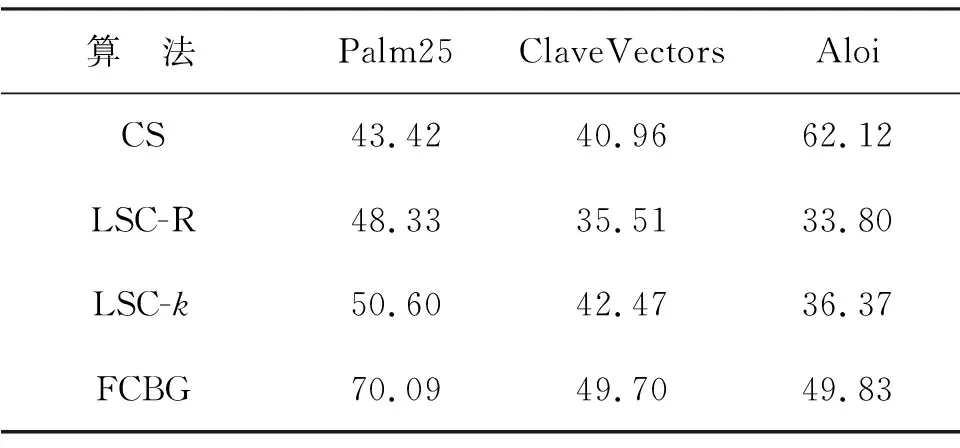
表2 三个数据集上的聚类准确率Table 2 Cluster accuracy on three data sets %

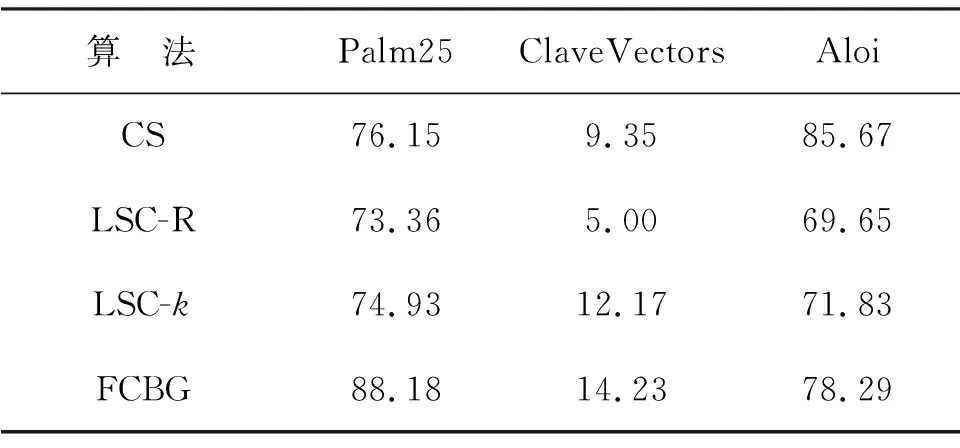
表3 三个数据集上的归一化互信息熵Table 3 NMI on three data sets %

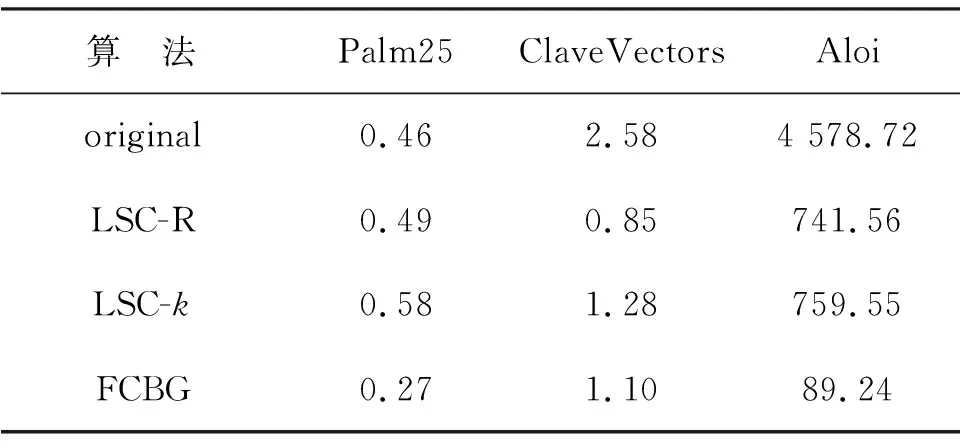
表4 三个数据集上的聚类时间Table 4 Clustering time on three data sets s

表4记录了算法总的运行时间．从表4可见，FCBG算法在3个数据集上进行聚类时，保持了和对比算法相近的运行时间．值得注意的是，FCBG算法在理论上时间复杂度要略大于LSC-R和LSC-k算法的时间复杂度，但在运行时出现了FCBG算法运行时间大于LSC-R和LSC-k算法运行时间的情况．这是因为在完成谱分析后进行离散化时，FCBG算法直接根据图的连通性得到聚类结果，时间复杂度可忽略不计，而LSC-R和LSC-k算法均需要通过在类似性矩阵F上执行k-means算法得到聚类结果．实验使用LSC-R和LSC-k算法的默认设置，k-means算法需重复10次，故所需时间极长．在不计算离散化步骤时间的情况下，LSC-R算法和LSC-k算法运行时间均短于FCBG算法所需时间．总体上来说，FCBG算法运行时间和对比算法相近，但更稳定．

结 语

本研究针对大规模谱聚类问题提出了一种基于二部图的快速聚类算法FCBG．初始阶段，FCBG算法采用随机采样从n个原始数据点中选择m个锚点；构图阶段，FCBG算法首先为原始数据点和锚点构建初始相似矩阵，然后对相似矩阵的归一化拉普拉斯矩阵施加秩约束，利用约束结果对相似矩阵进行更新，最后迭代得到聚类结果．对归一化拉普拉斯矩阵施加秩约束，可保证相似矩阵中连通分量数量恰好等于类簇数量．最终得到的二部图是稀疏的，且保持了清晰的聚类结构；FCBG算法计算复杂度与样本数目呈线性关系．真实数据集上的实验结果表明，FCBG算法性能优越、速度快，且图学习思想可应用于其他基于图的机器学习算法．