液体火箭POGO振动缩聚模型研究
王庆伟, 王小军, 张青松, 潘 辉, 谭述君
(1. 北京宇航系统工程研究所, 北京 100076; 2. 中国运载火箭研究院, 北京 100076;3. 大连理工大学 航空航天学院, 大连 116024)
POGO振动是液体火箭在飞行过程中由于结构系统与推进系统耦合而产生的一种纵向自激振动,Titan II、Diamond-B、Saturn V和我国的长征二F火箭上都出现过不同程度的POGO振动,其产生的纵向振动加速度对运载火箭的安全性和可靠性造成非常不利的影响,特别是对宇航员造成极大的生理痛苦[1-7]。因此,抑制POGO振动已成为液体火箭研制过程中重要环节之一。Rubin等将推进系统简化为单推进剂单发动机模型,推导了POGO振动产生的机理并提出了判断POGO稳定性的临界阻尼比判别法。Zhao等也利用简化的单推进剂单发动机推进系统模型,推导出五个无量纲的参数来判定POGO振动的稳定性并提出了耦合强度的概念。谭述君等[8]进一步完善了耦合强度理论,深入研究了系统阻尼比对POGO稳定性的非线性影响关系,指出临界阻尼比法的局限性并提出了临界耦合强度判别法,通过耦合强度和临界耦合强度的大小关系即可判断耦合系统稳定性。徐得元等[9]利用有理多项式逼近的方法提出了POGO系统振动特性的一种快速求解方法。郝雨等[10]得出了结构-推进耦合系统的二阶线性微分方程,并提出了通过求灵敏度进行推进系统参数优化的方法。唐冶等[11]对液体火箭推进系统频率特性进行了灵敏度分析。Oppenheim等[12]提出了一种POGO振动模型建模的有限元法,得出了状态空间形式的POGO振动模型。该方法广泛地应用于宇宙神二/半人马座和长征二F的POGO问题研究中。Wang等[13]在Oppenheim等的基础上提出了一种改进的模型,只选取节点上的相对脉动质量位移为变量,得出了维数减半的微分方程形式的POGO振动模型,不仅降低了计算量,而且可以用于时域仿真。张青松等[14]提出了基于键合图理论的POGO建模方法,建立了包含气路单元的POGO模型,通过特征值分析POGO振动的稳定性。赵治华[15]利用多体系统动力学方法,分析了包含结构纵横扭模型的液体火箭POGO振动稳定性。
由于燃料输送管较短,燃料输送系统的频率远高于结构系统的低阶频率。因此,将推进系统简化为单推进剂-单发动机模型,不仅可降低模型维数,且更便于研究POGO振动产生的机理及开展参数灵敏度分析。然而目前对单推进剂-单发动机推进系统模型的研究通常将输送管的方程简化为一个物理方程,或者直接忽略管路的柔性,作为不可压缩管路建模,只保留蓄压器的柔性和泵的气蚀柔性。该方法仅能体现出推进系统一阶频率与结构系统的耦合,无法体现推进系统高阶频率与结构系统的耦合。然而随着液体火箭的规模增大,液体输送管路长度不断增加,氧化剂输送管路的柔性体降低了推进系统二阶等低阶频率,且火箭规模的增大也导致结构系统的低频密集分布,推进系统的二阶及以上模态仍可能与结构系统不同模态产生耦合导致不稳定。然而由于泵、三通和蓄压器部件的存在,使得文献[13]中推进系统模型系数质量矩阵虽为非奇异阵,但是其刚度阵为非对称阵,阻尼阵为非比例阻尼或非瑞利阻尼阵,因此无法以传统的振型分解法将推进系统模型振型分解。进一步分析文献[13]中的模型可得出,输送管路单元的变量占了模型总变量的大多数。而且输送管路的不同单元具有相同的表现形式,因此可以将管路模型的质量阵、刚度阵和阻尼阵解耦。
为此,本文提出了一种推进系统模型缩聚的方法,以贮箱出口和蓄压器入口作为管路的边界条件,利用广义逆迭代法将所有输送管路的单元的质量阵、刚度阵和阻尼阵模态分解。选取重点关注阶次的推进系统管路的模态方程,与其余部件三通、蓄压器、泵和推力室组成缩聚后推进系统的模型。该模型既具有单推进剂-单发动机模型的维数低的优点,又包括推进系统不同阶次模态。因此可以方便地用于研究推进系统与结构系统不同阶次模态之间的耦合稳定性。
1 推进系统的模型
随着推进剂的消耗,结构系统的频率增大,推进系统的一阶频率往往与结构系统的某一阶频率存在交叉区,存在POGO失稳的风险。由于燃料输送系统的频率远高于结构系统的频率,因此本文建立的推进系统中只考虑氧化剂输送系统,但建模方法同样适用于燃料输送系统。氧化剂输送系统的示意图如图1所示,输送管路划分为n段,根据文献[12],每段管路单元的最大长度L满足
(1)
式中:a为有效当地声速,fu是关心的最高频率。

图1 推进系统示意图
文献[12]中给出了每种单元动力学方程的详细推导过程,在此不再赘述。图1所示模型中六类单元的方程形式如下所述。贮箱出口单元的方程为
(2)
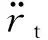
氧化剂输送管路划分为n段,每一段的方程为
(3)
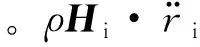
(4)
式中:Mp、Rp和Kp分别为质量阵、阻尼阵和刚度阵,由所有管路单元的刚度项、阻尼项和刚度项组成;U矩阵由各个管路单元方程中结构系统对推进系统的作用项组成;p1和ps分别为管路入口节点和出口节点的脉动压力。
三通是连接管路末端出口、蓄压器和泵入口的元件,其惯性和阻尼特性在与其连接的管路单元中考虑,其动力学方程为
ps=pa=pp
ws=wa+wp
(5)
式中:pa和pp分别是蓄压器入口和泵入口处的脉动压力;ws、wa和wp分别是管路末端出口、蓄压器入口和泵入口处相对脉动质量位移。
蓄压器作为调节推进系统频率特性的主要元件,其动力学方程为
(6)
式中:Ia、Ra和Ka分别为蓄压器的惯性、阻尼和刚度。当只将蓄压器作为纯柔性元件时,方程中只考虑蓄压器的刚度项,其方程为
pa=Kawa
(7)
泵单元的方程为
pp=Kp(wp-wc)
(8)
式中:Ip、Rp和Kp分别是泵的惯性、阻尼和刚度,m+1为泵的增益。将泵后管的惯性和阻尼添加到泵的惯性和阻尼项中,泵出口的脉动压力pc等同于推力室中的脉动压力。
推力室的方程为
(9)
式中:Rc为推力室的阻尼。
1.1 忽略蓄压器惯性和阻尼时的推进系统模型
因每个管路单元的方程形式相同,所以Mp和Kp为对称阵,Rp为瑞利阻尼阵,因此可以将管路单元的模型进行严格解耦。广义逆迭代法[16-17],避免了降阶扩维的复杂运算,仅通过简单的迭代即可将管路系数矩阵模态分解,得到管路的前m阶模态方程。
将蓄压器作为纯柔性元件时,综合式(5)~式(8),可得
pa=K*(ws-wc)
(10)
式中:K*=KaKp/(Ka+Kp)为等效刚度。根据式(5),将ps的表达式代入式(4)中,修正Kp矩阵的最后一个元素。以(Mp,Rp,Kp)得出的振型矩阵,对式(4)模态分解,令w=Φpz,得到
(11)

(m+1)K*Φp(n)z=0
(12)
式(11)和(12)即推进系统的缩聚模型,可以看出,当只取管路的某一阶模态时,推进系统仅由两个方程组成。
1.2 考虑蓄压器惯性和阻尼的推进系统模型
当考虑蓄压器惯性和阻尼时,三通出口端变量wp是一个独立变量,将式(6)代入式(4)中,令w=Φpz,对式(4)模态分解得出
(13)
综合式(6)和式(8),可得
Ka(Φp(n)z-wp)-Kp(wp-wc)=0
(14)
(15)

2 结构系统的模型
推进系统对结构的作用力包括管路单元、泵和推力室脉动压力对结构的作用力,因此在推进系统作用力下的结构系统的模态方程为
(16)
式中:Ms、Zs和Ωs分别为结构系统的模态质量阵、阻尼阵和刚度阵,q为结构系统的模态坐标,Φs为结构系统的振型矩阵。fd、fp和fc分别为管路单元、泵单元和推力室单元给结构的作用力。
每一段管路单元对结构系统的作用力为
(17)
式中:Ai和Aj分别为管单元入口和出口的截面积,Ni和Nj分别为管路单元入口和出口处的方向向量,g为重力加速度。
泵中流体对结构作用力为
fp=KpAp(wp-wc)N
(18)
式中:Ap为泵入口的截面积,N为泵入口处的方向向量。
推力室对结构的作用力为
fc=-NAtCfpc
(19)
式中:At为推力室喉部的截面积,Cf为推力室的推力系数。
将式(17)~(19)及推进系统节点上的脉动压力表达式代入式(16)中,可以得出将蓄压器作为纯柔性元件时结构系统的方程为
(20)
式中:方程最右端项的出现是因为将相对脉动质量位移替换作用力表达式中脉动压力时得出的项,体现了推进系统与结构系统耦合作用对结构惯性项的影响,是引起结构耦合频率变化的主要因素。特别地,将式(20)右端项中的K*替换为Kp即为考虑蓄压器惯性和阻尼时的结构系统方程。
3 POGO振动模型
3.1 忽略蓄压器惯性和阻尼时POGO振动模型
将蓄压器当作纯柔性元件时,以x=[z,wc,q]为状态变量,综合式(11),(12)和式(20),可得到缩聚后的POGO振动模型为

(21)
式中:
(22)
式(21)即模态缩聚后的POGO振动模型,可以看出,耦合模型的变量由管路单元的模态位移、推力室的相对脉动质量位移和结构的模态位移组成。耦合模型的维数N与管路模态变量个数N(z)、结构模态位移的个数N(q)的关系满足N=N(z)+N(q)+1。其中,N(z)和N(q)可以根据实际情况选择不同的维数。特别地,当N(z)与和N(q)分别取1时,耦合系统模型的维数为3,与改进的Rubin模型相比,模型的维数和计算量均大幅降低,且M矩阵、K矩阵也为非奇异矩阵,可以直接通过QR法计算耦合模型的特征值以判断系统稳定性。利用该缩模型,可以更有针对性地研究推进系统重要参数对POGO稳定性的影响。
3.2 考虑蓄压器惯性和阻尼时的POGO振动模型
综合式(13)~(15)以及式(20)(Kp替换K*时的结构系统方程),以x=[z,wp,wc,q]为状态量,即得考虑蓄压器惯性和阻尼项时的与式具有相同形式的POGO振动模型,其中M、R和K分别为
(23)
可以看出,M阵仍然为非奇异阵,也可以直接用QR法求解系统的特征值。模型的维度比式(22)的模型多了一个维度,即N=N(z)+N(q)+2。
4 算 例
用本文推导出的缩聚模型与改进的Rubin模型分别计算了某型号液体火箭在某个飞行时间段POGO稳定性,其中横坐标除以最大飞行时间进行了无量纲化,蓄压器设计为纯柔性原件,采用式所示的模型计算。图2和图3给出了不同飞行秒点结构系统与推进系统耦合频率与阻尼比的计算曲线。可以看出,随着飞行时间的增大,结构系统与推进系统的频率在0.9 s(s仅代表无量纲时刻)附近出现了接近和穿越,从图3中可以看出结构耦合阻尼比在0.9 s附近大幅降低,表明结构系统的稳定性降低,而推进系统耦合阻尼比大幅增大。以改进的Rubin模型的计算结果为基准值,缩聚模型的耦合频率与阻尼比的最大相对偏差如表1所示,结构系统耦合频率和阻尼比的最大相对偏差为0.032%和1.9%,推进系统耦合频率和阻尼比的最大相对偏差为0.55%和0.20%,因此本文推导出POGO振动缩聚模型不仅维数大幅降低,而且具有相当高的精度。

图2 不同飞行秒点结构系统与推进系统耦合频率
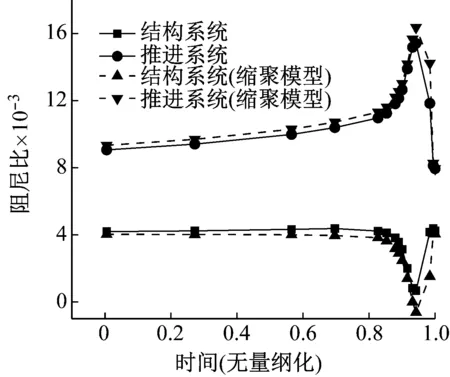
图3 不同飞行秒点结构系统与推进系统耦合阻尼比
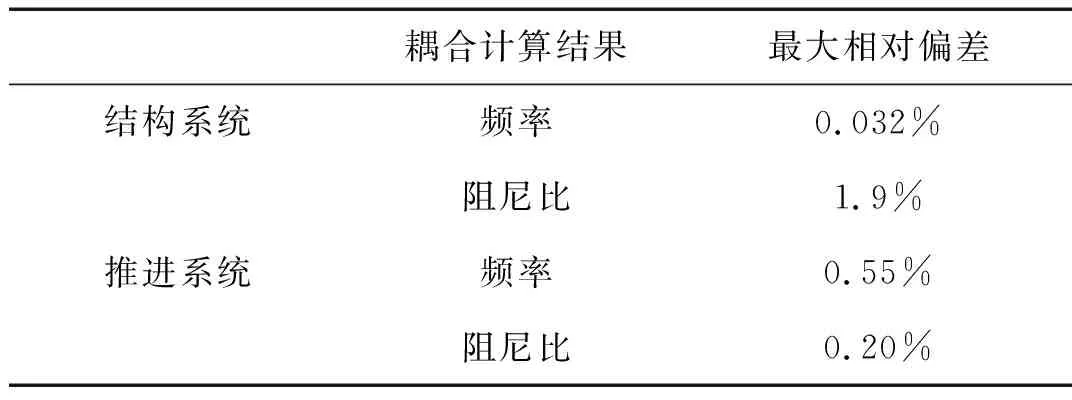
耦合计算结果最大相对偏差结构系统频率0.032%阻尼比1.9%推进系统频率0.55%阻尼比0.20%
蓄压器能量值对不同秒点模型耦合稳定性的影响如图4和图5所示,其中蓄压器能量值除以设计工况的额定值进行了无量纲化。由图4可以看出,蓄压器的能量值对不同秒点结构系统耦合阻尼比影响是不同的。随着蓄压器能量值增大,0.7 s结构系统耦合阻尼比变化很小,略有增大,0.93 s耦合模型的结构系统耦合阻尼比先大幅减小又大幅增大。说明0.93 s耦合模型的稳定性对蓄压器的灵敏度较高。与图3对比可以看出,0.7 s耦合模型的结构系统与推进系统的频率差别较大,0.93 s耦合模型的结构系统与推进系统频率差别较小,两者频率的接近造成了耦合作用。
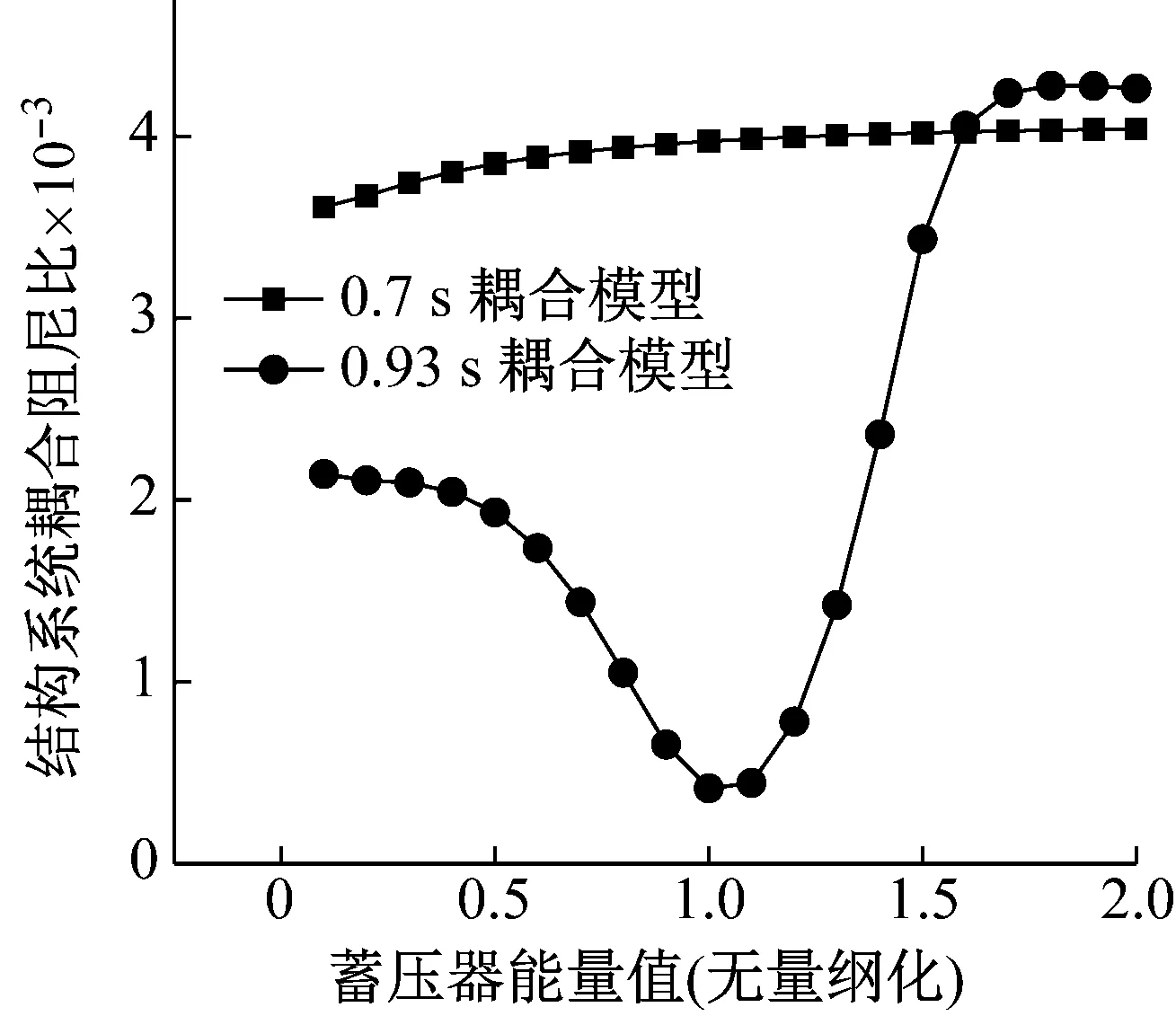
图4 蓄压器能量值对不同秒点结构系统耦合阻尼比的影响
图5给出了0.7 s和0.9 s推进系统的阻尼比随蓄压器能量值增大的变化情况,可以看出,随着蓄压器能量值的增大,两个秒点的耦合模型中的推进系统阻尼比都大幅降低。但0.9 s耦合模型推进系统的阻尼比在0.6 s~1.5 s区间有一向上的“鼓包”,通过对比图4可以得出是推进系统与结构系统耦合作用的结果。
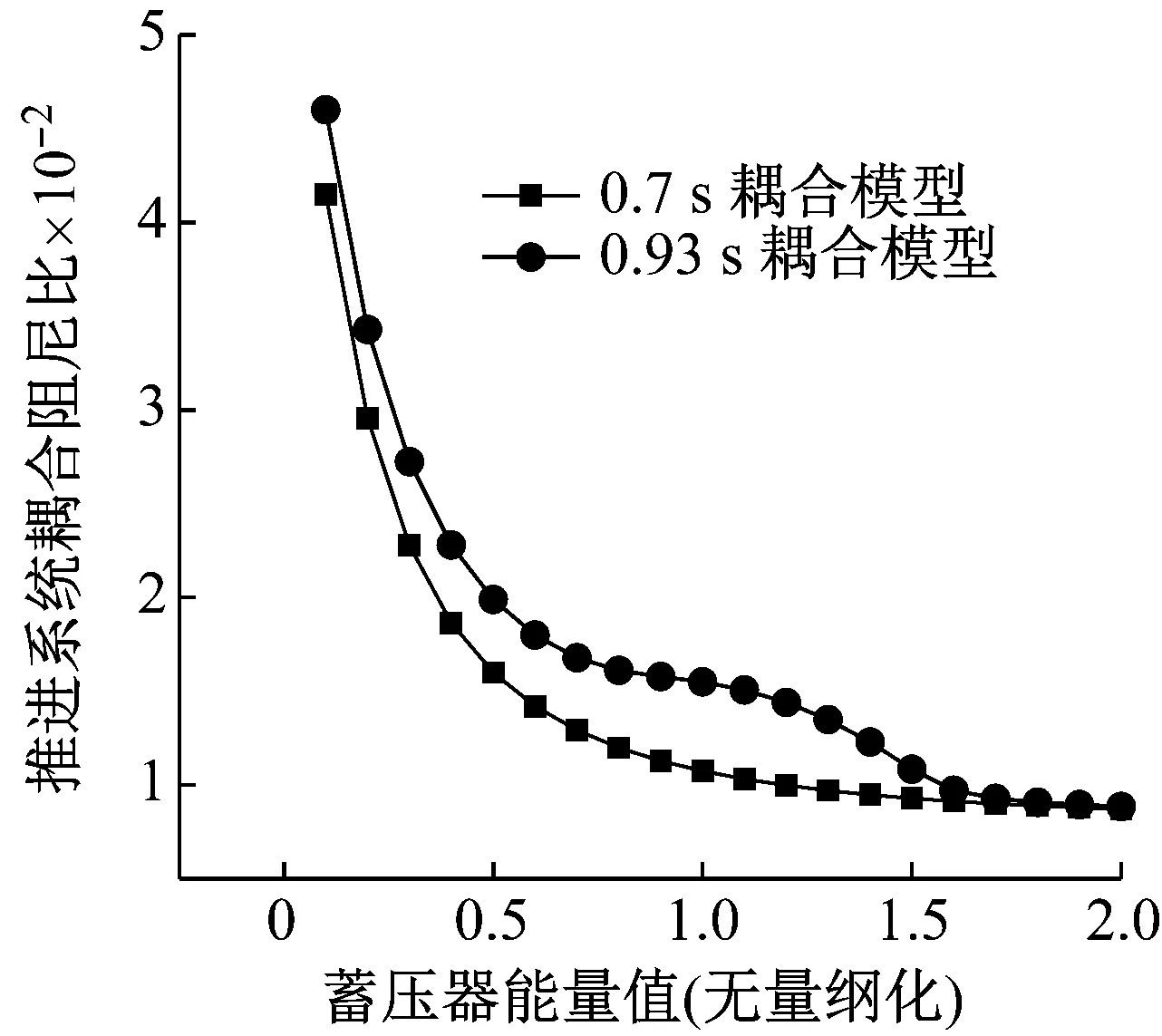
图5 蓄压器能量值对不同秒点推进系统耦合阻尼比的影响
当考虑蓄压器的惯性和阻尼时,可以用式(23)所示的模型研究蓄压器惯性和阻尼等参数对POGO稳定性的影响。图6给出了蓄压器惯性对0.7 s和0.9 s耦合模型中结构系统耦合阻尼比的影响曲线。可以看出,蓄压器的惯性对0.9 s模型中的结构耦合阻尼比影响较大,随着蓄压器的惯性的增大,且这种影响也是非单调的。
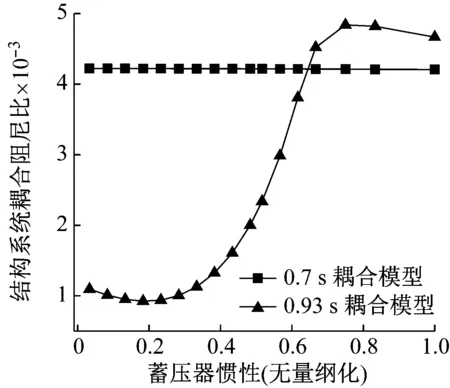
图6 蓄压器惯性对不同秒点结构系统耦合阻尼比的影响
5 结 论
本文提出了建立缩聚POGO振动模型的方法,分别推导了将蓄压器作为纯柔性元件和考虑蓄压器惯性和阻尼时的POGO振动缩聚模型。与改进的Rubin模型相比,缩聚模型的维度大幅降低,从而大幅降低计算量。算例表明缩聚后的POGO振动模型具有很高的精度。基于POGO缩聚模型分别计算了某型号液体火箭蓄压器能量值、惯性对0.7 s和0.93 s耦合模型POGO稳定性的影响。研究得出,蓄压器的能量值和惯性对不同时间点结构耦合阻尼比具有不同的影响,且这种影响是非单调的。当结构系统与推进系统频率较接近而导致结构耦合阻尼比大幅降低时,若蓄压器设计为纯柔性元件,合理调节蓄压器的能量值可以增大结构耦合阻尼比,当考虑蓄压器的惯性和阻尼时,合理的增大蓄压器的惯性也可以增大结构系统的耦合阻尼比,增强结构系统的稳定性。

