支承刚度变化下风电齿轮传动系统的非线性动力学特性

向 玲， 高 楠， 唐 亮， 郭鹏飞

(华北电力大学 机械工程系,河北 保定 071003)

齿轮传动系统是航空航天、高铁运输和风能利用等领域中重要的机械设备。近年来风力发电机作为清洁能源的发电设备已得到全球的推广和利用，但由于此类设备常在苛刻的环境下工作，其故障率也逐步增加，且齿轮传动故障位居前列。其中，行星齿轮传动是风电传动系统的关键部件之一，但由于其结构复杂、内外激励因素较多，会存在一些非线性因素。因此，齿轮传动系统的动力学行为及其机理的研究，对提高系统效率和延长其工作寿命有重要意义。多年来，众多学者致力于齿轮系统的动力学研究。邱星辉等[1]从系统动力学建模及求解、动力学特性和优化设计等方面对目前风电行星齿轮传动系统的研究进行了综述；Kahrarman[2]建立了单级行星齿轮传动系统的动力学模型并对其振动模态做了分析；Lin等[3]考虑多个自由度建立了行星齿轮传动系统的模型并进一步求解分析了系统固有频率和振型，讨论了陀螺效应和时变啮合刚度对其的影响。Sheng等[4]建立了行星齿轮传动系统的平移-扭转非线性动力学模型，以系统内外啮合副齿侧间隙的变化作为分岔参数，引入阻尼的影响，深入研究了不同齿侧间隙变化下行星齿轮传动系统的动力学特性。李晟等[5]以两级行星齿轮传动系统为分析模型，研究了内外激励下系统的分岔与混沌特性。林腾蛟等[6]以多级齿轮传动系统为研究对象，求解并分析了齿侧间隙、转速及负载等因素对整个系统的影响。Wang等[7]建立了风电齿轮传动系统的纯扭转非线性动力学模型，讨论了阻尼的变化对系统非线性行为的影响。田亚平等[8]以风力发电机混合轮系为建模对象，求解并分析了该系统的动力学行为。杨军[9]对行星齿轮传动系统固有振动特性进行了研究，分析了包含支承刚度和时变啮合刚度在内的多个参数对固有频率及振型的影响。佘凯等[10]考虑支承刚度和支承阻尼，建立了直齿轮副的非线性动力学模型，分析支承刚度变化下系统的动力学行为。李贵彦[11]以弧齿锥齿轮为研究对象，建立了8自由度的非线性动力学模型，以支承刚度和啮合间隙为分岔参数对其进行分析，探讨了参数变化下系统的状态。Xiang等[12]建立了含摩擦的齿轮-轴承非线性动力学模型，分析了支承刚度和激励频率变化下系统的非线性动力学特性。

当前许多学者已经建立了不同齿轮传动系统的动力学模型，并考虑了多个非线性因素，研究分析了参数的变化对系统的影响。本论文在此基础上，以1.5 MW风电齿轮传动系统为研究对象，建立一级行星齿轮传动及两级平行轴齿轮传动系统的平移-扭转非线性动力学模型，模型考虑了时变啮合刚度、综合啮合误差、齿侧间隙和太阳轮支承刚度，进一步地讨论和分析太阳轮支承刚度的变化对系统动力学特性的影响。分析结果为深入研究风电齿轮传动系统的非线性动力学特性和故障机理等提供理论参考。

1 非线性动力学建模与振动微分方程

1.1 非线性动力学模型

图1所示为某风电齿轮传动系统动力学模型示意图，该模型由一级行星齿轮传动和两级平行轴齿轮传动串联构成，所有齿轮均为直齿圆柱齿轮。传动系统输入端为行星架，输入扭矩为Tin，输出端为高速端齿轮系，输出扭矩为Tout。行星齿轮系包括太阳轮、行星架、行星轮和内齿圈，分别用s、c、pi(i=1,2,…,N)和r表示。平行轴齿轮传动包含低速端齿轮传动和高速端齿轮传动，共包含4个齿轮，分别以g1、g2、g3和g4表示。为简化计算，假设全部齿轮主体部分为刚体，齿牙为弹性体,行星齿轮在行星架均布且参数一致，传动轴为刚性短轴且两端轴承具有相同刚度和阻尼，忽略各轮系齿间摩擦力的影响。行星架(各齿轮)的扭转位移表示为θm(m=s,pi,c,g1,g2,g3,g4)，太阳轮径向位移为xs、ys，建立8+N自由度动力学模型，其广义坐标为即

q={θs,xs,ys,θc,θp1,…,θpi,θg1,θg2,θg3,θg4}

齿轮内部激励包括时变啮合刚度、啮合阻尼和啮合误差，分别由kj、cj、ej(j=spi,rpi,g1g2,g3g4)表示，其中spi代表行星齿轮传动内啮合副，即太阳轮和各行星轮啮合副、rpi代表行星齿轮传动外啮合副，即内齿圈和各行星轮啮合副、g1g2和g3g4则分别代表平行轴齿轮传动中的低速端齿轮啮合副和高速端齿轮啮合副。

图1 风电齿轮传动系统动力学模型

齿轮啮合副刚度的变化是时变的，根据直齿轮啮合副刚度的特点可近似的采用周期矩形波来表示各齿轮副间啮合刚度。为进一步简化计算，本文采用以基于啮合频率ωj为基频的Fourier级数展开表示时变啮合刚度，取一次谐波项，公式可表示为[13]

kj=kmj+kajsin(ωjt+φj)

(1)

式中，kmj、kaj分别为各啮合副的平均啮合刚度及刚度变化幅值，φj为各啮合副啮合刚度变化幅值的初相位。

为使方程能够顺利求解，引入齿轮副间的相对位移xj，公示表达为

xg1g2=rg1θg1+rg2θg2-eg1g2(t)

xg3g4=rg3θg3+rg4θg4-eg3g4(t)

xrpi=rpiθpi-rcθccosα-erpi(t)

(i=1,2,…,N)

(2)

式中，ej(t)为综合啮合误差，是静态传递误差和齿轮制造误差的总称，同时也是系统内部激励来源之一，公式以啮频周期性变化的正弦函数来表示[14]

ej=Ejsin(ωjt+ηej)

(3)

式中:Ej为各啮合副综合啮合误差幅值；ηej为各啮合副综合误差初相位。

齿侧间隙非线性函数[15]表示为

(4)

系统中各啮合副动态啮合力由弹性恢复力和阻尼力构成，可表示为

(5)

式中，Mj是各齿轮副间的等效质量。

1.2 相对坐标下的无量纲振动微分方程

(6)

最终得到该系统的相对位移坐标下的无量纲振动微分方程表达式如下所示

(7)

式中，

2 系统求解及分析

该方程采用4～5阶变步长Runge-Kutta法进行求解，为了消除系统的瞬态响应，略去前1 500个周期，计算所得数值结果以分岔图、最大Lypapunov指数图(以下称LLE图)、时间历程图、FFT频谱图、相图及Poincaré截面图作为分析工具对系统分岔及混沌特性进行研究说明。以兆瓦级风机作为示例，取齿轮传动系统基本参数Pin=1.5 MW，Λ=94，ξ=0.03，α=20°，N=3，齿轮基本几何参数和计算参数如表1所示。

2.1 系统随激励频率变化的动力学特性

图2 系统随激励频率变化的分岔图(ki=1)

行星齿轮系行星架c太阳轮s行星轮p内齿圈r分度圆半径rm/m0.470.190.280.75转动惯量Im/(kg·m2)85.35.7529.6平均啮合刚度kmj/(N·m-1)1.31×10101.486×1010刚度变化幅值kaj/(N·m-1)4.96×1095.12×109压力角/(°)20平行轴直齿轮系低速端g1低速端g2高速端g3高速端g4分度圆半径rm/m0.530.110.370.09转动惯量Im/(kg·m2)3060.5939.90.17平均啮合刚度kmj/(N·m-1)3.76×1095.12×108刚度变化幅值kaj/(N·m-1)7.25×1081.33×108

图3 系统随激励频率变化的最大Lyapunov指数图(ki=1)

结合两图分析可知，随着激励频率的增大，系统存在丰富的非线性行为，期间出现多个跳跃点和分岔点，系统多以激变和倍分岔的途径进入混沌运动。

当激励频率Ω在范围0.001～0.413 5时，系统处于单周期或拟单周期运动，期间伴随阵发性混沌运动，对应的LLE也出现突变现象。当Ω在0.413 5～0.439的范围内，系统进入混沌，LLE大于0。随后系统回归至拟单周期运动，在Ω=0.46时，系统分岔为拟2周期运动。当Ω=0.464 9时，发生跳跃现象，然后系统经激变进入混沌运动。随着激励频率的增大，系统逐渐变化为拟2周期，在Ω=0.521 5时，发生又一次跳跃现象，系统进入短暂的单周期运动后发生了再一次跳跃现象后重新进入混沌。当Ω=0.589时，系统经激变进入单周期，经倍分岔后系统进入混沌运动，且混沌范围明显增大，对应的LLE也呈现增大的趋势，仅在激励频率Ω=0.872 5时，系统由混沌激变为2周期，对应的LLE也出现突降，随后经短暂的倍分岔后回归混沌。

图4所示为系统在支承刚度比ki=0.5时，系统随激励频率变化的的分岔图。对比图2可知，当支承刚度减少时，系统总体运动情况不变，仍然以拟周期运动和混沌运动为主，但混沌区域明显增强，如激励频率Ω在0.445～0.505的区域。而且，在Ω=0.8附近的周期窗口也明显减小。

图4 系统随激励频率变化的分岔图(ki=0.5)

图5是支承刚度比ki=3时，系统随激励频率变化的分岔图，与ki=1和ki=0.5不同的是，系统在激励频率处于0.302 5～0.325的区间内，出现了混沌运动。对比图2和图4可知，系统的混沌运动有所抑制，出现了多个多周期窗口，如范围在0.758 5～0.784和0.902 5～0.975 5等。在当激励频率Ω在0.758 5～0.784的范围内，系统由混沌经倒分岔进入2周期运动，后又经激变进入混沌。当激励频率Ω在0.902 5～0.975 5的范围内，系统变化状态为混沌→8周期运动→6周期运动→2周期运动→4周期运动→8周期运动→混沌。

图5 系统随激励频率变化的分岔图(ki=3)

2.2 系统随支承刚度变化的的动力学特性

以太阳轮支承刚度ks作为分岔参数，取刚度比ki在0.001～10区间，激励频率Ω=1时进行分析，得到全局分岔图(含局部细化图)及LLE图如图6和图7所示。可知，ki在0.001～0.081的范围内，系统处于2周期运动，LLE小于0，其中ki在0.097～4.977区间，系统经激变进入混沌运动，期间出现多个倒分岔现象或短暂的多周期窗口，如在1.281～1.313、1.953～2.241和2.417～2.449的范围等，可见对应的LLE出现突降现象。随后，系统由混沌进入2周期运动，经分岔为4周期运动后又回归至2周期，当ki=8.193时，系统再次发生分岔为4周期运动，直到ki=9.569，系统经激变重新回到2周期运动并保持不变。由图7可知，在期间发生了多次阵发性混沌运动，其对应的LLE指数也是大于0的。

图6 系统随支承刚度比ki变化的分岔图及其细化图

图8～图12表示了系统经倒分岔由混沌进入2周期运动的变化过程，分别以系统在不同支承刚度下的时间历程图、频谱图、相图和Poincaré截面图做以说明。当ki=1.665时，系统处于混沌运动，如图8所示。在相图中相轨迹是无规则的运动，Poincaré截面为无规则的点集，时间历程图无明显规律可循，对应的频谱图出现Ω/2分频成分并存在明显的连续边带。图9所示为系统在ki=1.905时所呈现的混沌运动，对比图8，相图无规则轨迹逐渐聚拢且以内八轨迹为主，Poincaré截面有两个点集，频谱图上出现Ωn/2分频成分，n为正整数，不同的是Ω/2分频高于基频并存在些许连续边带。当ki=1.985时，如图10所示，系统为8周期运动，频谱图上出现Ωn/8分频成分，相图轨迹为8个封闭曲线，Poincaré截面图为8个点。当ki=2.081时，系统处于4周期运动，如图11所示。在频谱图中可见其Ωn/4的分频成分，其中Ω/2分频幅值最高，相图为4个封闭轨迹，Poincaré截面为4个点。当ki=2.161时，系统为2周期运动，如图12所示。同样，在频谱图中存在Ωn/2分频成分，Poincaré截面为2个点，相图轨迹呈现为2个交叉的封闭曲线。

图8ki=1.665时系统的时间历程图、频谱图、相图及Poincaré截面图

Fig.8 The time series, FFT spectrum, phase diagram and Poincaré map whenki=1.665

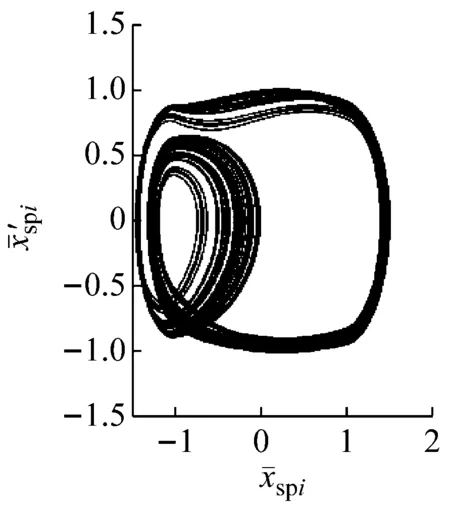
图9ki=1.905时系统的时间历程图、频谱图、相图及Poincaré截面图

Fig.9 The time series, FFT spectrum, phase diagram and Poincaré map whenki=1.905

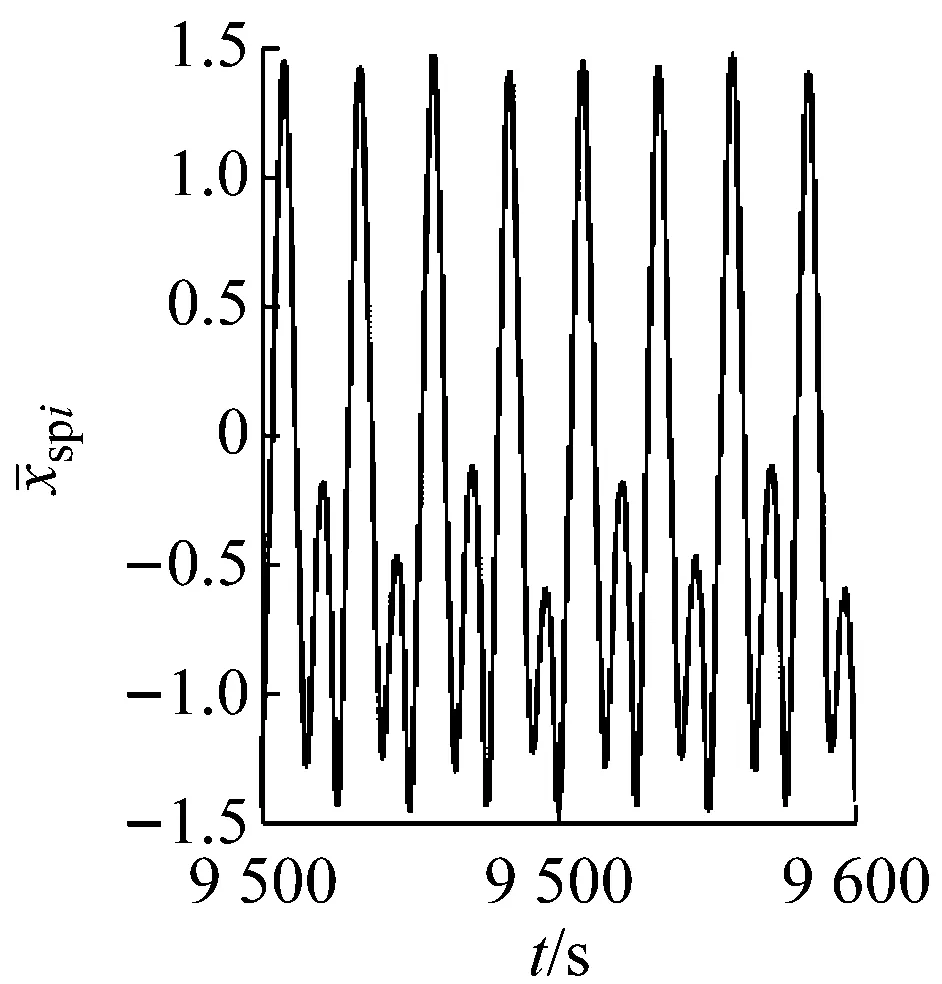
图10ki=1.985时系统的时间历程图、频谱图、相图及Poincaré截面图

Fig.10 The time series, FFT spectrum, phase diagram and Poincaré map whenki=1.985

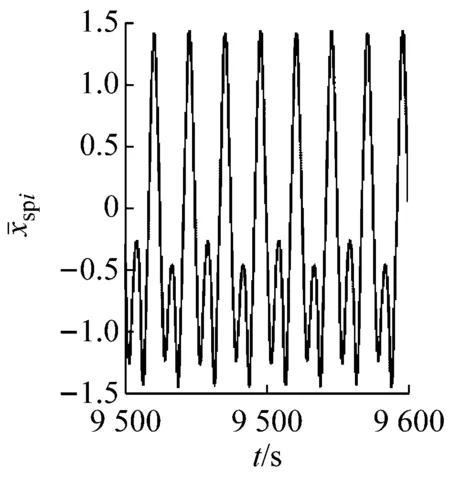
图11ki=2.081时系统的时间历程图、频谱图、相图及Poincaré截面图

Fig.11 The time series, FFT spectrum, phase diagram and Poincaré map whenki=2.081

综上，支承刚度会对系统产生影响，同时表现出丰富的非线性动力学行为。支承刚度的提高会使系统出现由周期进入混沌的现象，但继续增大则仍会回归至周期状态。因此在设计或作业时，应避开支承刚度的分岔点和混沌区域。

图12ki=2.161时系统的时间历程图、频谱图、相图及Poincaré截面图

Fig.12 The time series, FFT spectrum, phase diagram and Poincaré map whenki=2.161

3 结 论

在风电齿轮传动系统中，齿侧间隙等的非线性因素可能会引起整体系统的不稳定性，而持续工作状态中的支承刚度也会出现变化，从而导致系统出现分岔行为和混沌运动，破坏系统的稳定性，而混沌运动是系统不断地由某种轨道突跳到另一个轨道上去的无规则运动，表示了系统不可预测的行为和轨道的永不重复性，会导致系统寿命减少、增加疲劳作业时间和提高系统磨损的可能性，进而产生噪声，严重时则会致损。在设计中，应避开混沌状态的范围，采取安全、符合要求的作业范围。

通过全局分岔图、时间历程图、FFT频谱图、相图及Poincaré截面图可以定性对系统进行分析，利用全局或单点最大Lyapunov指数图可以定量的对系统进行分析，从而可以更为精确的确定系统的运动状态，保证机器的正常运行。

(1) 考虑齿轮非线性因素，如时变啮合刚度、综合啮合误差和齿侧间隙，建立了风电齿轮传动系统的非线性动力学的平移-扭转模型，引入支承刚度作为分岔参数，分析了系统在不同支承刚度下随激励频率变化的动力学特性。支承刚度的增大会对系统随激励频率变化下的运动状态产生影响，使进入混沌延迟并出现周期运动窗口。

(2) 利用多种分析工具对系统响应结果进行分析，在时变啮合刚度、综合啮合误差和齿侧间隙强非线性因素的作用下，系统在太阳轮支承刚度的变化下会表现出丰富的分岔特性及混沌现象，如周期运动、拟周期运动和混沌运动，进入混沌运动的途径以激变和倍周期分岔途径为主。本文分析结果可对风电齿轮传动系统的设计、安装及减振方面提供理论参考。