自适应鲁棒控制在机械臂轨迹跟踪中的应用*

张 程，张 卓

(1.吉林大学珠海学院，广东 珠海 519041；2.广东科学技术职业学院，广东 珠海 519041)

0 引言

从控制理论的角度看，多自由度机器人系统是一个复杂的动态耦合系统[1]，其数学模型具有明显的复杂性和非线性，如何设计一种能较好地应对这类强不确定性和非线性系统的轨迹跟踪控制方案是一个重要课题。在实际应用中，面对由系统自身或外界原因造成的不确定干扰因素，常规PID控制不能很好的满足机器人系统的控制要求，存在速度较缓慢、位姿误差较大的问题。一些学者采用智能算法与传统算法结合，以解决上述缺陷或不足，例如神经网络、模糊理论及鲁棒控制等智能理论[2-5]。针对上述问题，本文采用自适应鲁棒控制算法以解决仿人型机械臂的控制优化问题，利用SolidWorks进行仿人型机械臂机械结构的自主设计，采用Lagrange-Euler法建立机械臂的动力学模型，设计鲁棒控制律及相关控制参数，并通过直线和曲线两种目标轨迹的跟踪控制实验，验证了该方法具有明显优于常规控制器的跟踪控制性能。

1 机械臂结构及动力学模型

1.1 机械结构设计

利用SolidWorks进行机械臂结构的自主设计，建立仿人型机械臂的三维模型。带有外轴的仿人型机械臂机械结构如图1所示，其具有肩关节、肘关节、腕关节(末端执行器)，由电机驱动，可以实现3个自由度运动。其肩关节运动范围-180°～180°，肘关节运动范围-170°～170°，腕关节运动范围-90°～90°。并设计将肩关节固定在外轴机构上以扩展该机械臂的作业范围。该机器臂适用于物体追踪、检测、切割以及扫描等作业。标称物理结构参数如表1所示。

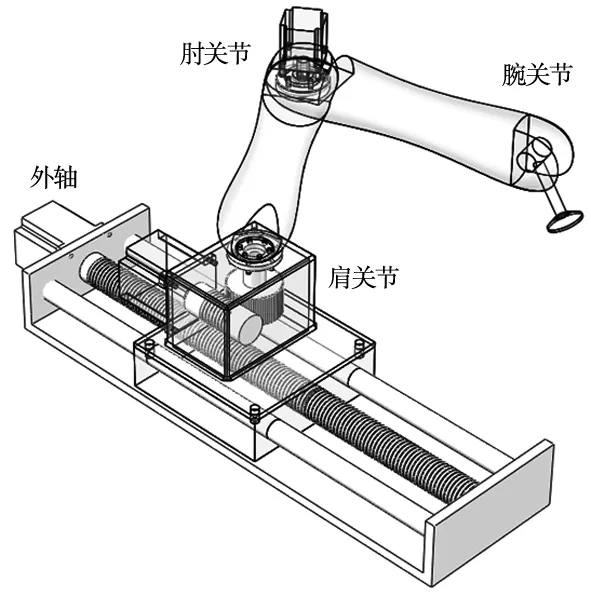
图1 带有外轴的仿人型机械臂机械结构

1.2 动力学模型分析

机械臂动力学主要研究作用于机械臂上的力和力矩，建立机械臂动力学方程主要有Lagrange-Euler和Newton Euler两种方法[6]，本文选择Lagrange-Euler建立机械臂动力学方程。

仿人型机械臂的运动坐标如图2所示，考虑目标工作空间为x轴和y轴所构成的平面，腕关节(末端执行器)保持相对该平面的近似固定位姿，故主要考虑肩关节和肘关节的大范围运动模式。将工作空间中的关节末端节点直角坐标(xq,yq)转为关节角位置(q1,q2)的问题，以建立工作空间关节末端节点直角坐标(xq,yq)的动力学模型。

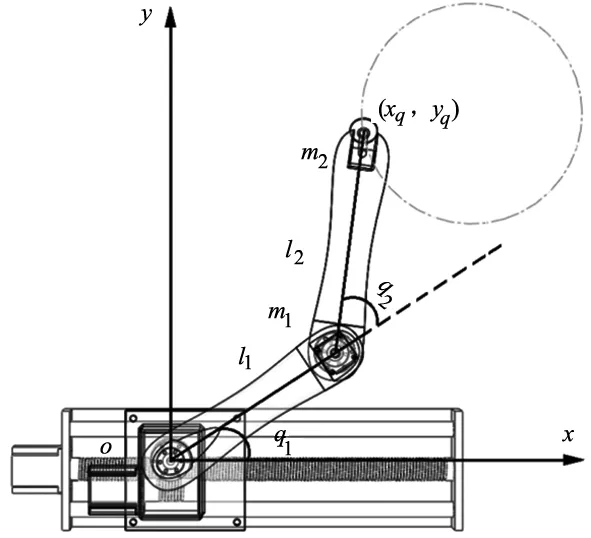
图2 机械臂运动坐标示意图

采用Lagrange-Euler法建立机械臂动力学方程，可得机械臂末端在工作空间中的坐标位置为[6]：

xq=l1cosq1+l2cos(q1+q2)

(1)

yq=l1sinq1+l2sin(q1+q2)

(2)

构建两坐标间数学关系，求其平方和得：

(3)

从而可解得：

(4)

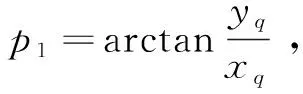
(5)

考虑本系统为刚性机械手，其动态特性为：

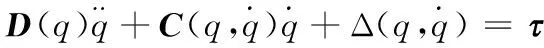
(6)

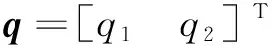
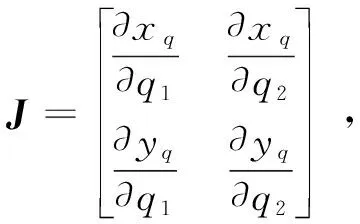
(7)

上式具体可以表达为：

(8)

其中，

2 自适应鲁棒控制器设计

主要解决自适应鲁棒控制器设计问题。鲁棒控制器具有处理干扰、快变参数等能力[7-8]，控制目标为：即使系统中存在参数不确定性、外部干扰、未建模动态特性或其他不确定性，仍然能够保持其在稳定性、跟踪误差或其他指标方面的性能表现[9-11]，以确保机械臂的控制系统具有良好的运动特性。

2.1 控制算法设计

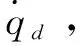
e(t)=q(t)-qd(t)

(9)

(10)

考虑上述Lagrange-Euler动力学方程(6)，得到鲁棒控制器控制律u(t)：

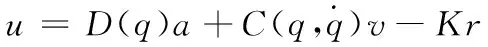
(11)

其中v，a和r给出如下：

(12)

(13)

(14)

其中，K和Λ是定常正值增益的对角矩阵。将控制律(11)带入到方程(6)，得到闭环系统方程：

(15)

(16)

其中，θ0是一个固定的表征参数向量，同时δθ是一个附加输入项，根据以下方式来设计：

(17)

其中,ρ是参数不确定性的界线。

2.2 系统稳定性分析

定义辅助信号如下：

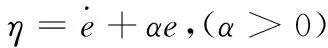
(18)

可将式(15)表示为：

(19)

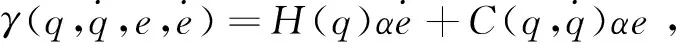
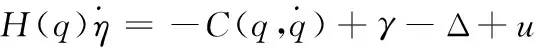
(20)

即控制律设计为：

u=-Kη-γ-v

(21)

(22)

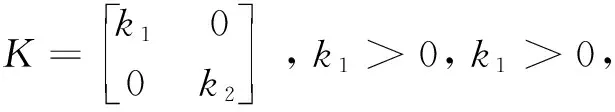
根据定理可证该控制器对于有界的建模误差，跟踪误差一致终值有界[7,11]，且当模型误差为零时，跟踪误差为零。

3 机械臂鲁棒控制轨迹跟踪仿真

利用Simulink工具箱建立仿人型机械臂控制系统模型。考虑到实际应用中，机械臂的复杂运动轨迹均可以分解为线性直线运动和非线性曲线运动的叠加，故本文通过直线轨迹和曲线轨迹两种方式，验证自适应鲁棒跟踪控制效果，并同常规PID控制下的轨迹跟踪效果进行比对，得到实验数据及结论。

3.1 直线运动轨迹跟踪及结果分析

采用S函数输入目标轨迹函数，选取直线运动函数进行轨迹跟踪实验，目标轨迹生成指令如下：

function sys=mdlOutputs(t,x,u)

xd=0.2;

yd=0.2×cos(pi/2×t)+0.2;

根据上述算法，采用S函数设计控制器，控制律增益取k1=k2=54，ε=0.001，得到直线轨迹跟踪仿真结果如图3至图7所示。图3和图4分别为直线运动下的常规控制和鲁棒控制的轨迹跟踪示意图，图5和图6分别为直线运动下的常规控制和鲁棒控制的位置跟踪曲线。图7为直线运动下的两种控制方法的跟踪误差对比。

图3 常规控制轨迹跟踪(直线运动)

图4 鲁棒控制轨迹跟踪(直线运动)

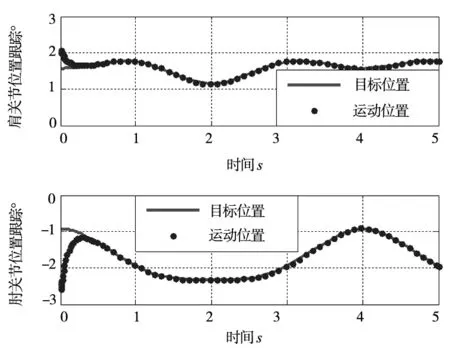
图5 常规控制位置跟踪曲线(直线运动)

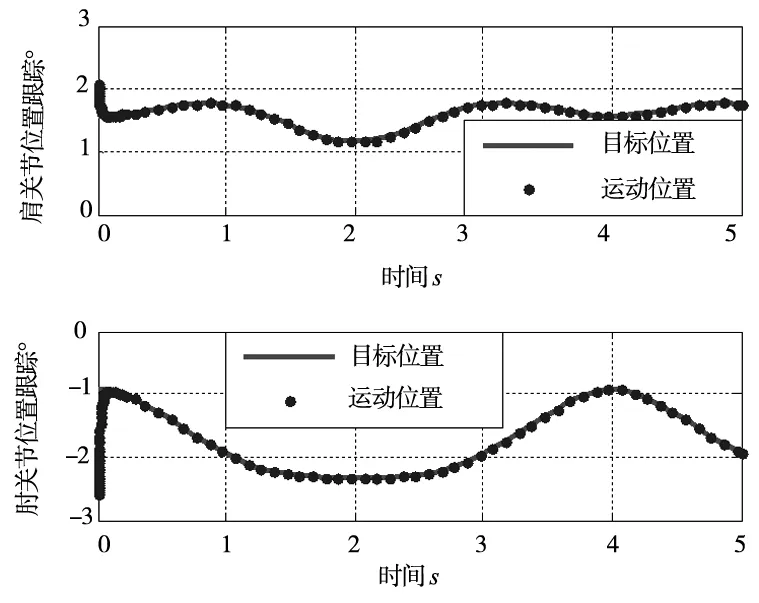
图6 鲁棒控制位置跟踪曲线(直线运动)

图7 两种控制方法的跟踪误差对比(直线运动)

由图5可以明显看到，常规控制方法的收敛时间长，而图6中鲁棒控制方法的跟踪误差在较短时间内收敛到0、跟踪速度快。由图7中两种控制方法对比，以肘关节为例分析：常规控制方法稳定后最大误差达到0.018°，收敛时间为0.75s，而鲁棒控制方法的最大误差为0.001°，收敛时间为0.25s，相对于常规控制器，鲁棒控制的收敛速度提升67%，位姿跟踪精度提高44%。综上可得，在直线运动下鲁棒控制在跟踪性能和响应速度上均优于常规控制器。

3.2 曲线运动轨迹跟踪及结果分析

以典型的圆周曲线运动为例进行轨迹跟踪，采用S函数输入目标轨迹函数，选取圆周运动函数进行轨迹跟踪实验，目标轨迹生成指令如下：

function sys=mdlOutputs(t,x,u)

xd=0.12×sin(pi/2×t)+0.25;

yd=0.12×cos(pi/2×t)+0.15;

根据上述算法，采用S函数设计控制器，控制律增益取k1=k2=54，ε=0.001，得到曲线轨迹跟踪仿真结果如图8～图12所示。

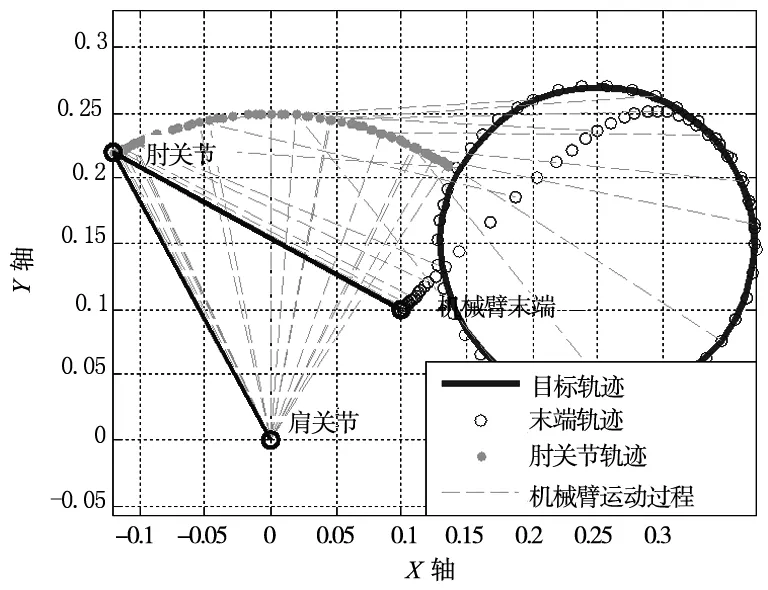
图8 常规控制轨迹跟踪(圆周运动)

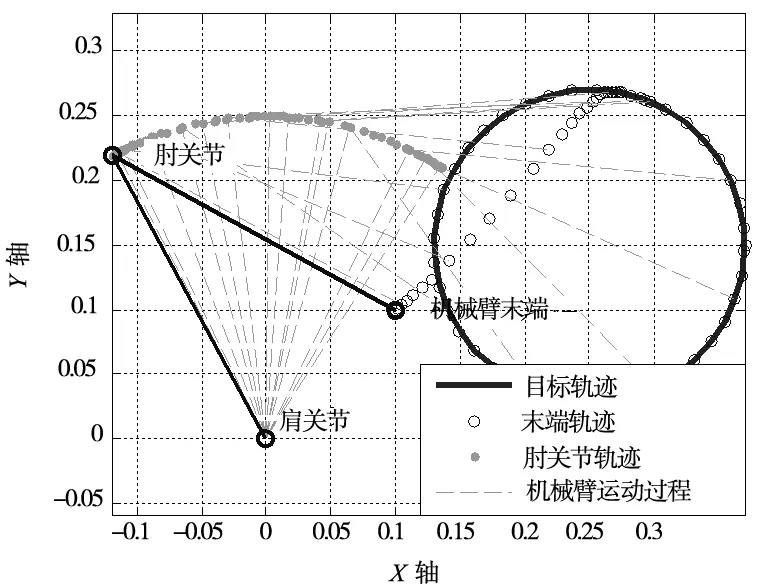
图9 鲁棒控制轨迹跟踪(圆周运动)

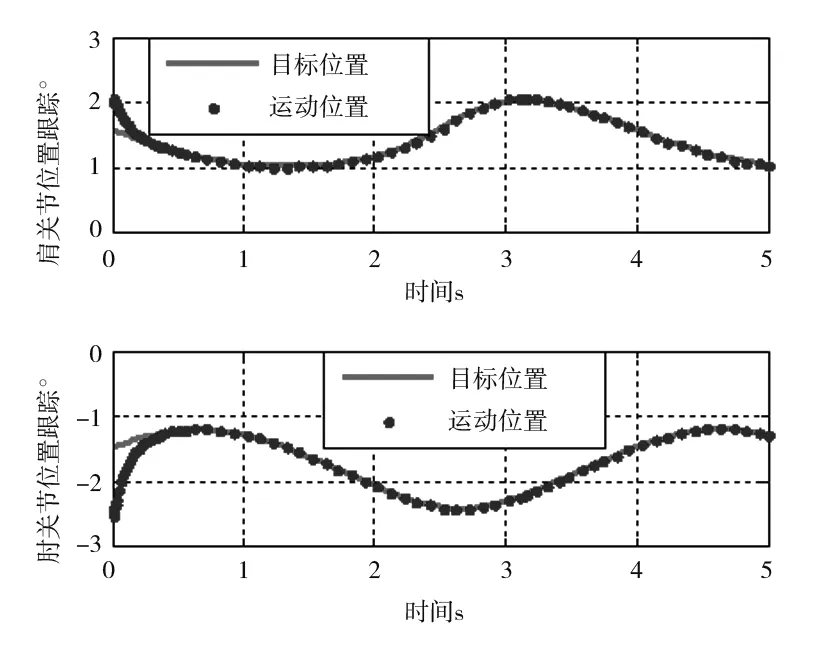
图10 常规控制位置跟踪曲线(圆周运动)

图11 鲁棒控制位置跟踪曲线(圆周运动)

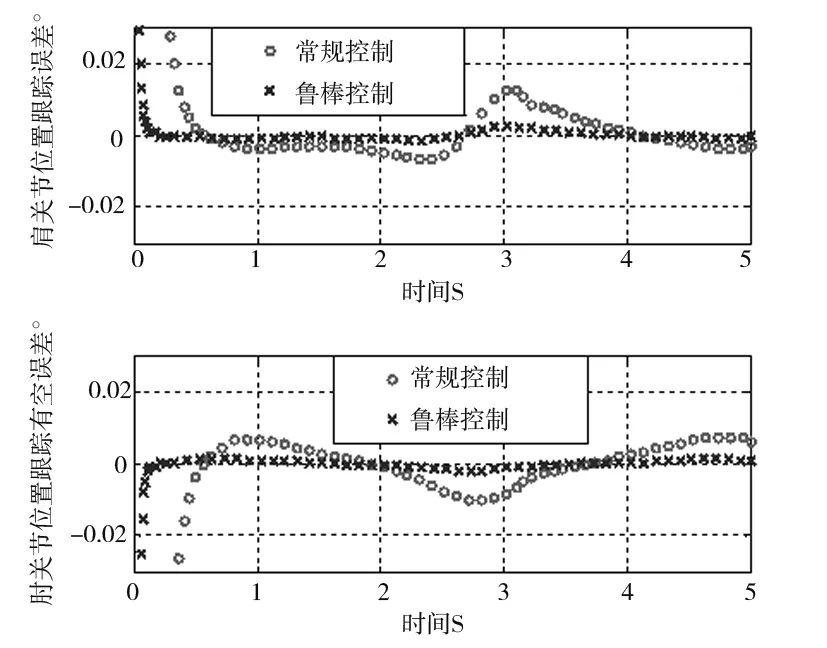
图12 两种控制方法的跟踪误差对比(圆周运动)

由图10可以明显看到，与直线轨迹跟踪的情况类似，常规控制方法的收敛时间长，而图11中鲁棒控制方法的跟踪速度更快。由图12中两种控制方法对比，以肘关节为例分析：常规控制方法稳定后最大误差达到0.008°，收敛时间为1s，而鲁棒控制方法的最大误差为0.001°，收敛时间为0.3s，相对于常规控制器，鲁棒控制的收敛速度提升70%，位姿跟踪精度提高87.5%。综上可得，在圆周运动下鲁棒控制在跟踪性能和响应速度上亦均优于常规控制器。

通过上述两组仿真结果及实验分析可得，鲁棒控制器能迅速、准确地跟踪期望轨迹，在跟踪性能和响应速度上均优于常规控制器，能够保证机械臂系统达到更好的跟踪性能。

4 结 论

本文以仿人型机械臂为研究对象，设计了一种鲁棒自适应控制策略，利用SolidWorks进行机械臂结构的自主设计，利用Simulink工具箱进行机械臂控制系统模型设计，通过直线和曲线两种运动轨迹的跟踪控制进行验证，实验结果表明，相对于常规控制器，该控制器可以更为准确地控制机械臂的末端轨迹，跟踪速度快且位姿控制精度高。该控制方法具有较好的可行性及一定的工程参考性。