基于体对角线误差检测的数控机床几何误差辨识方法研究*

李金和

(天津大学 机构理论与装备设计教育部重点实验室，天津 300354)

0 引言

机床运动精度的检测方法有三种：一是利用球杆仪(DBB)测量刀具的轨迹误差[1]。二是利用干涉仪测量机床的各项几何误差[2]。三是利用跟踪仪测量机床空间位置坐标值，从而实现对机床各项几何误差的分离[3]。上述方法不能完全满足机床高精度、快速检测的要求[4]。随着ASME B5.5[5]和ISO230-6[6]机床检测标准的引入，使得体对角线综合误差测量和空间综合误差测量技术被广泛应用在误差检测领域。研究一种基于空间体对角线误差检测技术的几何误差源辨识方法，对加快我国掌握高精尖制造技术并实现高端装备制造业的转型升级具有重要的理论意义和实用价值。干涉仪的辨识方法应用广泛。Zhang G和Quang R等提出了误差检测的22线法[7]。刘又午等提出了14线法和9线法，提高了误差检测效率[8]。范晋伟、田越等改进了14线法，提高了辨识模型的稳定性[9]。Soichi Ibaraki[10]等提出了在有安装误差情况下能准确辨识机床的空间误差元素的新方法。郭俊杰[11]等使用Leica 激光追踪仪研究了基于该测量仪器的多站分时测量方法。

Etalon AG在2014年研制出一种Laser TRACER的测量仪器，测量过程用类似于“GPS 定位”的多边定位原理，能够实现机床误差的快速标定和精密测量，且将误差测量范围扩展到整个工作空间。Laser Tracer有两大优点：①摒除了测角误差对整体测量精度的影响[4]。②利用球面误差小于50nm的标准球代替传统的反射镜[12]。这种设计结构,测距精度较高，已被波音、德玛吉、NIST和NPL等成功使用并受到广泛认可[13]。

1 机床对角线误差的评价方法

测量体对角线上测点的空间误差，按照ISO230-6检测标准每米至少5个测点，正反向至少分别测量5次，以综合考虑机床的反向间隙；评价机床对角线误差几何精度不考虑沿对角线的重复精度，而仅计算沿对角线的双向系统偏差E和反向间隙B。

设三个线性轴长度分别为X﹑Y和Z，则体对角线与三个坐标轴之间的夹角余弦分别为：

假定体对角线上m(m≥5)个测点的空间误差，正负方向分别测量n(n≥3)次。记机床运动部件第j(j=1～n)次向第i(i=1～m)个测点沿正负两个方向趋近时测得三个坐标误差分量Δxij↑和Δxij↓、Δyij↑和Δyij↓、Δzij↑和Δzij↓，则该测点沿体对角线两个方向上的单向位置偏差为：

Δdij↑=Δxij↑cosα+Δyij↑cosβ+Δzij↑cosγ

Δdij↓=Δxij↓cosα+Δyij↓cosβ+Δzij↓cosγ

该测点沿体对角线方向的单向平均位置偏差以及双向平均位置偏差分别为：

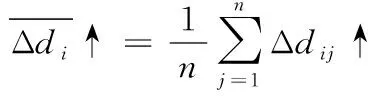
该测点沿体对角线方向的单向和双向定位系统偏差分别为：

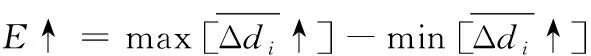
该测点沿体对角线的反向偏差以及整个对角线的反向偏差：

假设4条体对角线的双向定位系统偏差分别为E1,E2,E3,E4,则体对角线双向系统偏差Ed=max[E1,E2,E3,E4]。

假设4条体对角线的反向偏差分别为B1,B2,B3,B4,则体对角线反向偏差Bd=max[B1,B2,B3,B4]。

2 误差检测和辨识方法研究

2.1 测点误差

图1 测量仪器炮塔位置标定

(1)炮塔位置标定[13]。以三个坐标轴的交点为原点，各滑板的运动方向为正方向建立坐标系。

如图1所示，网格为工作空间pi(xi,yi,zi)(i=1,2,…,n)为第i个测点；Aj(j=1,2,…,6)为炮塔的第j个坐标位置。以A1的标定，说明标定过程。已知第i个测点的坐标为pi，第i个测点距离炮塔位置A1的长度为L1i。误差测量中，变换6次炮塔的安装位置。每次，人为测量炮塔到靶标的初始距离并输入到测量系统，由于测量的不准确而引起死程误差，设死程误差为Lj(j=1,2,…,6)。设炮塔第一个位置坐标为A1(x,y,z)，对测量点pi(xi,yi,zi)距离按照两点距离公式建立如下方程组：

炮塔标定时，实际测点数n≥4，方程组为超定，可用最小二乘法求解。将第i个方程两边取平方并展开得等式

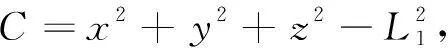
据最小二乘原理,存在解(x,y,z,L1,C),使得目标函数F取得极小值。

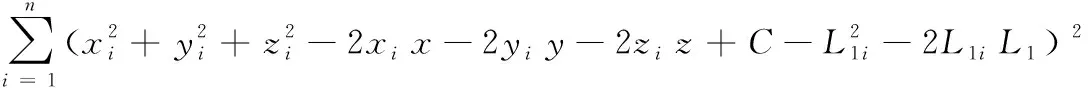
则必有一阶偏导为零，同时二阶偏导恒正。将方程组按未知数(x,y,z,L1,C)整理成矩阵格式：

当系数行列式不为零时，方程组有唯一确定的解，从而炮塔的第一个坐标A1以及死程误差L1得以标定。重复上述过程，即可标定出炮塔在A2～A6处的坐标，以及死程误差L2～L6。

为了提高标定精度，将标定出的位置作为初始值，使用Matlab中的最优化迭代算法，最优化6个炮塔的位置坐标，优化目标函数为：

(1)

式中，(xaj,yaj,zaj)为最优化后第j个炮塔坐标，(xi,yi,zi)为靶标的第i个坐标。

(2)测点实际位置标定

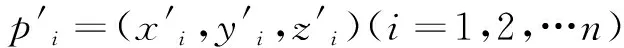
(3)测量点空间误差确定

测点真实位置pi′，减去该点的理想位置pi即可得到该点的空间误差:

Δri=(xi′-xi,yi′-yi,zi′-zi),i=1,2,…n。

pi′=(xi′,yi′,zi′)为第i个测点的实际坐标，而pi=(xi,yi,zi)为该点的理想坐标，Δri为该点空间位置误差向量。

2.2 辨识方法研究

使用多项式函数描述机床的位置相关几何误差和位姿误差.并基于机床的误差模型建立机床几何误差的多项式参数向量与机床末端位置误差之间的映射模型。通过误差可辨识性分析,可一次性辨识得到数控机床的所有几何误差源。

(1)多项式误差参数辨识方程

三个平动轴的位置误差(包括3项定位误差和6项直线度误差)为：

(2)

三个平动轴的转角误差(包括3项俯仰角、3项偏摆角、3项滚转角误差)为：

(3)

式中，δij,k表示位置误差δi(j)的多项式模型中第k个多项式系数；εij,k表示转角误差εi(j)的多项式模型中第k个多项式系数；k为n阶多项式中幂的阶数。pδi(j)、pεi(j)分别为描述位置误差δi(j)、转角误差εi(j)的系数向量，hδi(j)、hεi(j)为对应的坐标位置矩阵，且可以写成如下形式：

式中，j为X轴或Y轴或Z轴的当前坐标，靶标的坐标(x,y,z)已知，故坐标位置矩阵hδi(j)、hεi(j)亦为已知量。

将式(2)和式(3)代入与X轴位置相关的几何误差向量ex=(δx(x)δy(x)δz(x)εx(x)εy(x)εz(x))T中有：

同理可以得到：

ey=Hypy和ez=Hzpz

(4)

式中,px,py,pz以及Hx,Hy,Hz为X、Y、Z轴的位置相关几何误差参数向量以及与其相对的位置坐标矩阵。

可以得到21项几何误差与其对应的多项式系数向量之间的关系：

(5)

Δr3×1=Aε=AHp=M3×(18n+3)p(18n+3)×1

式中，Δr为工作空间中某一点处机床末端位姿误差向量,H为映射矩阵，M为该点对应的误差映射矩阵，p为21项几何误差多项式系数向量，包括位置相关几何误差的18n项多项式系数向量和位置独立的3项垂直度向量。

(2)多项式系数向量的辨识方程组

Δr中含有3个误差分量，组成含有3个误差辨识方程的方程组，而向量p中共有18n+3个未知系数，方程组无法求解，增加测点数，使得方程的数量大于等于未知系数的数量即可求解。假设一共m个测量点，对于第i个测量点，(i=1,2,…,m)，Δri=Mip。考虑到有m个测量点，则多项式系数向量p的辨识方程组为：

式中，n为多项式的阶数；m为测量点总数；Δr为在第i个测量点误差向量；Mi为第i个测点对应的误差映射矩阵。当3m≥18n+3，可以辨识出多项式系数向量p。

(3)辨识方程组的可辨识性分析

将第i个测点的误差映射模型拆分成如下形式 ：

式中，Mji为该测点与第j(j=1～21)项几何误差多项式向量,pj相对应的误差映射矩阵Mi中第j列列向量。假设Mi中仅第一列和第二列线性相关，即等式M1i=αM2i(α≠0,i=1,2,…,m)成立，写成矩阵形式 ：

上式中各列均线性独立，辨识出的参数为αp1+p2，无法将p1和p2分离出来，所以应直接去掉Mi中相关的参数p1和p2式中一列，以及待辨识参数矩阵Mi中相应的参数M1i或M2i。这样矩阵满秩，即可将剩余的误差参数向量辨识出来，对于线性相关的列向量可以通过其他方法求解。首先对误差辨识矩阵Mi进行相关性分析。将矩阵Mi拆分成如下形式：

式中，Mxi、Myi、Mzi、Msi分别为与数控机床三个坐标轴X、Y、Z和垂直度误差相关的误差映射矩阵，多项式系数向量p可辨识的核心条件为误差映射矩阵Mi中的列向量均相互独立。

通过观察矩阵Mxi、Myi、Mzi、Msi，需要检测n个测点以及炮塔变换6个位置才能辨识所有几何误差对应的多项式系数，故Mi某一列向量中只要包含有x、y、z、wxow、wyow、wzow6个变量中任意一项，该元素所在的列向量一定不能由其它任意列向量线性表示。很显然Mxi、Myi和Mzi中角度误差的对应列向量以及Msi一定线性无关，需要特别注意的是Mxi、Myi和Mzi中位置误差的对应列向量可能线性相关，非线性相关条件为测量空间的起始点的三坐标值互不相等，即x≠y≠z。

(4)采用分段多项式和三次样条辨识方法

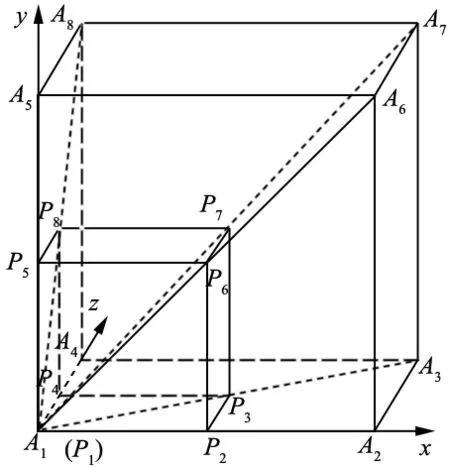
图2 测量空间网格划分示意图

将工作空间均等划分为n份，每份在三个坐标轴方向上的分量为：

与此同时，可以得到第一个子空间的8个顶点的坐标为：

P1(x0y0z0)P2(xmy0z0)
P3(xmymz0)P4(x0ymz0)
P5(x0y0zm)P6(xmy0zm)
P7(xmymzm)P8(x0ymzm)

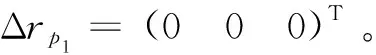
P1：误差零点，不须考虑。

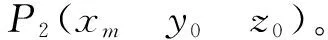
式中，A18,P2=[A(:,[1:6]),zeros(3,12)]。

同理，点P1～P8对应的误差映射矩阵。

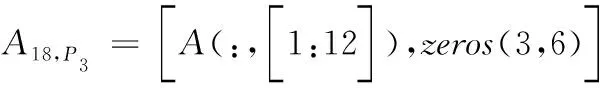
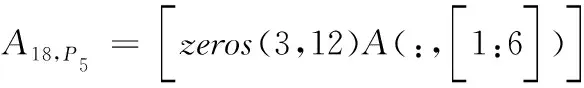
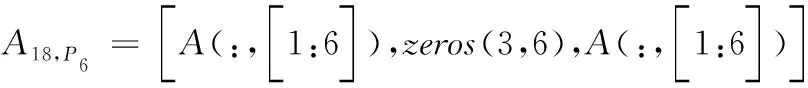
联立上面7个等式得到：

Hε18=Δr

式中误差映射矩阵和末端误差为：

由此，第一个子空间上ε18即可求解，剩余的n-1个子空间的几何误差可参照以上方法求解。得到三坐标轴线上各空间网格点的21项几何误差，误差辨识矩阵的可辨识性分析以及后续的仿真实验均和多项式误差辨识方法相同。

3 计算机仿真

3.1 仿真优化目的和方法

用Matlab进行仿真优化，第1步：设定测量空间的两个对角点在机床坐标系中的坐标、测量轨迹线组合方案、炮塔相对靶标的6次安装位置、用于拟合位置相关几何误差多项式的阶数n以及每条测量轨迹线上均匀分布的测点个数m；第2步：初始给定一组多项式系数向量用于仿真(记为P0)； 第3步：使用式Δr=Aε，计算初始机床末端位姿误差向量Δr0；第4步：在Δr0上叠加服从均值为零、标准差为σ的正态分布N(0,σ2)的扰动误差，以模拟测量噪声及其它不确定因素，得到实际误差向量Δr1。第5步：计算误差映射矩阵M的条件数和秩，用最小二乘法计算得到实际多项式系数p=(MTM)-1MTΔr1和相对误差ε；第6步：评价测量轨迹，当误差映射矩阵M满秩，条件数较小，且相对误差足够小，测量轨迹仿真优化结束。 多次重复以上过程，直到找到一组最优化测量轨迹使得辨识精度足够高，误差补偿效果足够好。

3.2 两步解正则化方法

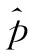
由此，辨识得到多项式系数向量，并结合式(4)计算当前位置的21项几何误差，和初始给定的21项误差作比较，评价该辨识方案的辨识效果。

3.3 仿真优化结果

选取三个坐标轴、三条面对角线以及四条体对角线，在十条轨迹线上均匀选取11个测点。仿真中，采用LaserTRACER测量得到的一组21项几何误差作为初始误差ε0，用误差模型计算位置误差Δr0，在Δr0叠加一个高斯噪声δ～N(0,0.5)模拟实测误差，而后辨识出实际的21项几何误差值，两步解正则化方法中，正则化参数α=0.093178。

(a)Z轴滚转角误差辨识效果

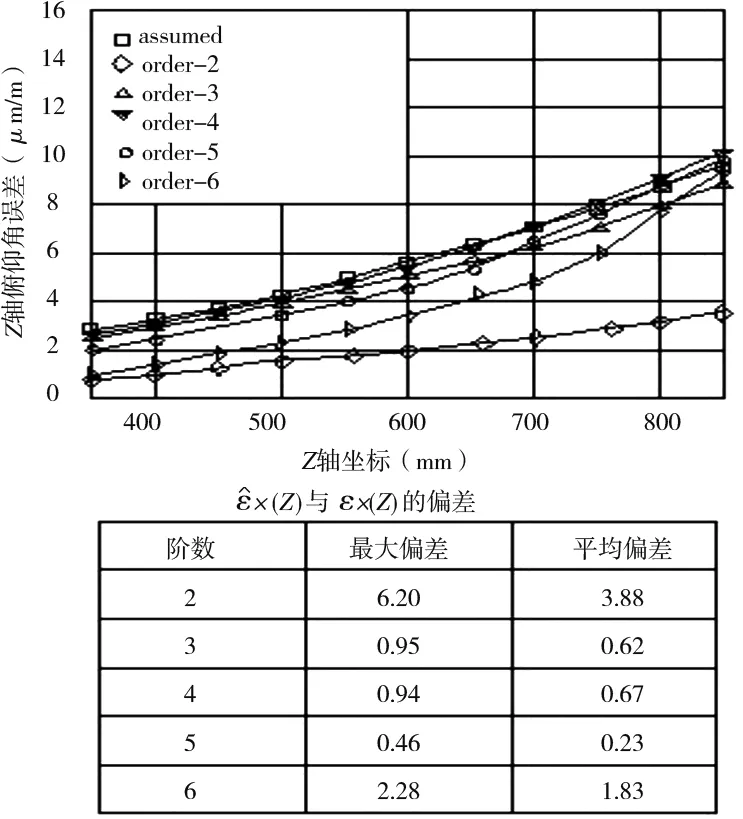
(b) Z轴俯仰角误差辨识效果

(c)X轴定位误差辨识效果

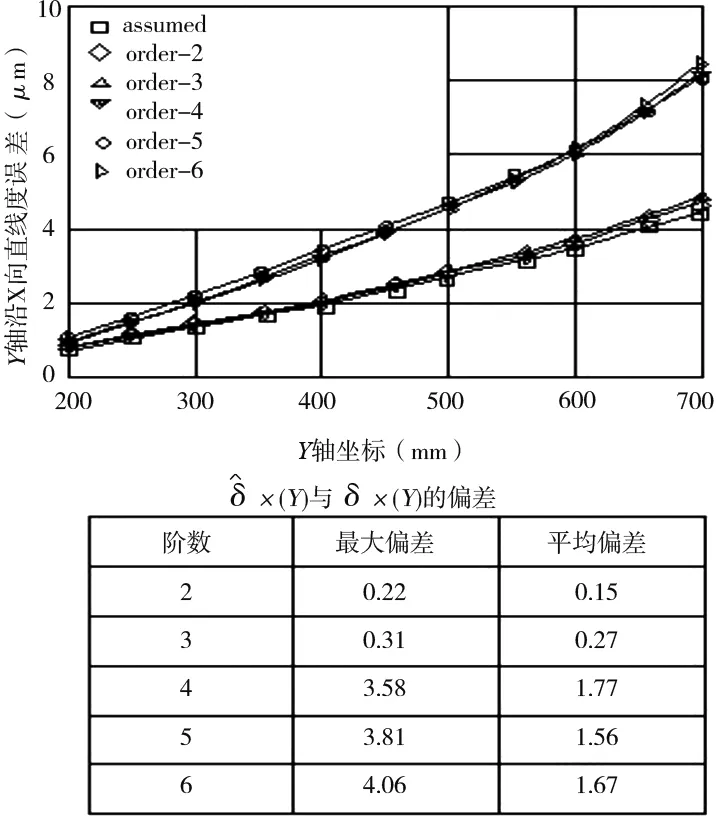
(d) Y轴沿X向直线度误差辨识效果

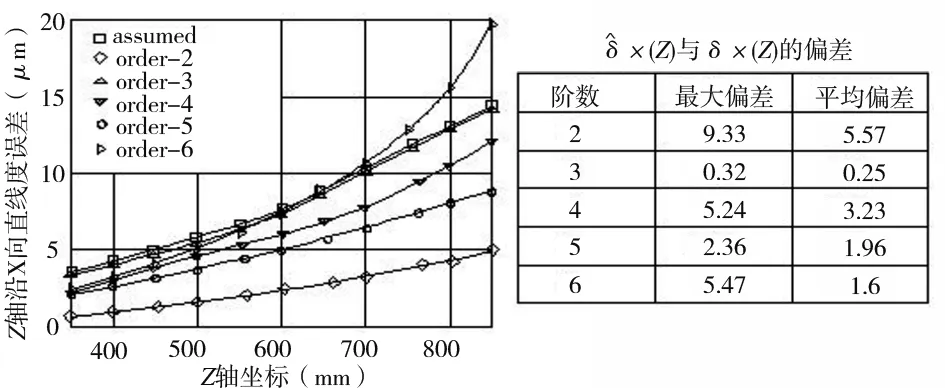
(e)Z轴沿X向直线度误差辨识效果

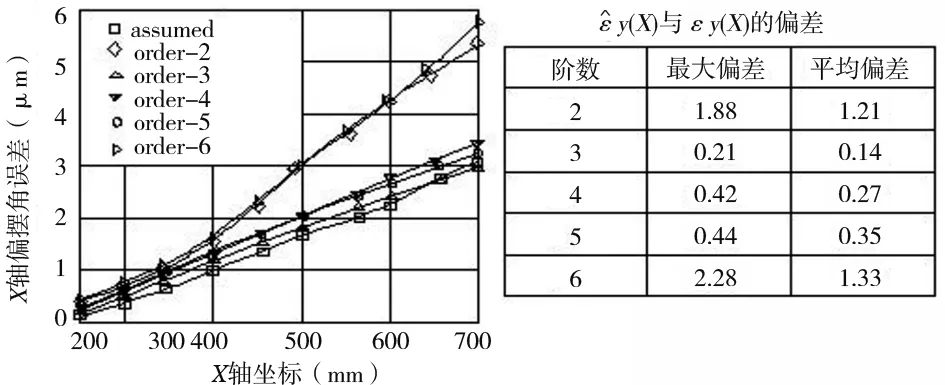
(f) X轴偏摆角误差辨识效果图3 6项关键位置相关几何误差初始值与辨识值比较

辨识得到的21项几何误差和初始给定的21项几何误差值作比较，以评价辨识效果。其中，Z轴滚转角误差εZ(z)，垂直度误差εyz、εxz，Z轴俯仰角误差εx(z)，X轴定位误差δx(x)，Y轴沿X向直线度误差δx(y)，Z轴沿X向直线度误差δx(z)，X轴偏摆角误差δy(x)和垂直度εyz等9项关键几何误差对体对角线误差的全局灵敏度较大且依次递减，误差辨识过程中应严格控制其公差。9项关键误差的辨识值和初始值的对比结果如图3和表1所示。

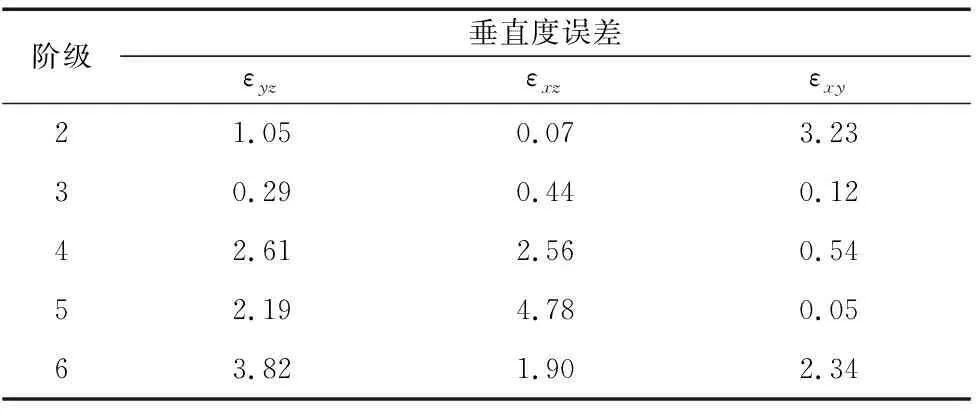
表1 垂直度误差假定值与辨识值差异

从均方误差的角度来比较辨识效果的优劣。记给定的21项初始几何误差为e1～e21，由辨识算法辨识得到的21项几何误差为e1(n)～e21(n)，n为仿真中设定的多项式的阶数n=2～6。则不同的多项式阶数对应的均方误差为：

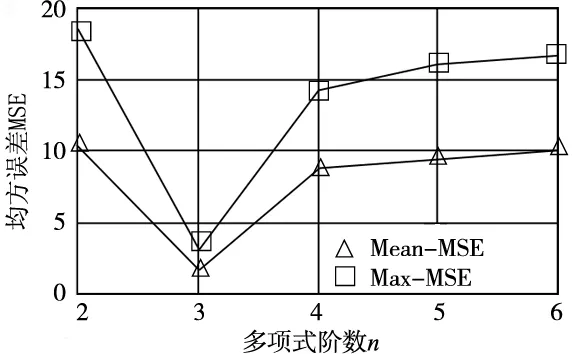
图4 n=2～6时辨识结果的均方误差比较

如图4 所示，阶数为3时辨识误差最大值和平均值对应的均方误差都达到最小，故选阶数为3。

4 实验对比验证

以一台精密卧式加工中心为研究对象，与使用干涉仪XL-80检验关键几何误差作比较，验证前述检测和辨识方法正确性和有效性。实验在20±0.5℃的恒温实验室。

4.1 跟踪仪Laser TRACER误差测量结果

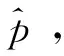
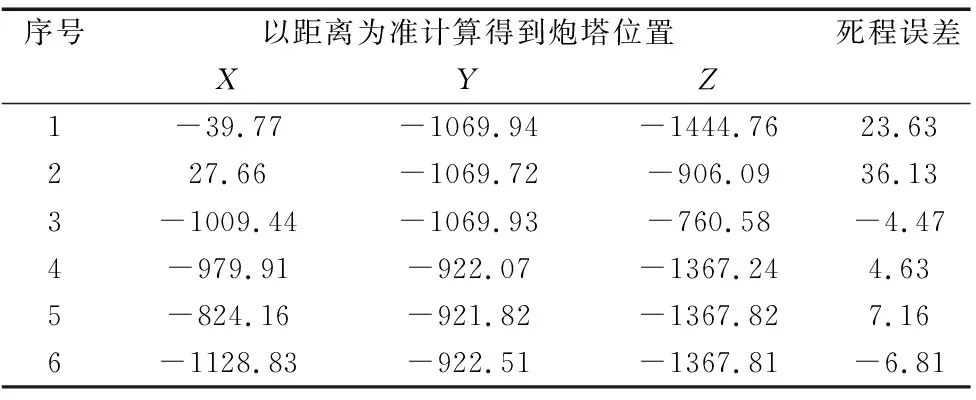
表2 6个炮塔位置的坐标(mm)

4.2 干涉仪误差测量实验及测量结果

机床的进给速度为4000mm/min，采用位置触发自动采集数据，越程量为10mm，公差为0.5mm，读数稳定性为0.001mm，3个坐标轴的测量行程分别为X(-700～-200)、Y(-700～-200)、Z(-850～-350)，3个坐标轴每间隔50mm停机4s，每个坐标轴11个测点，正负方向各采集5次以将数控机床的间隙误差包括在内。

表3 干涉仪误差测量实验及测量结果

4.3 辨识效果对比

如表4所示为由辨识得到的21项几何误差与干涉仪测量结果的对比，式中位置相关几何误差的辨识值与测量值均由两点法计算得到。

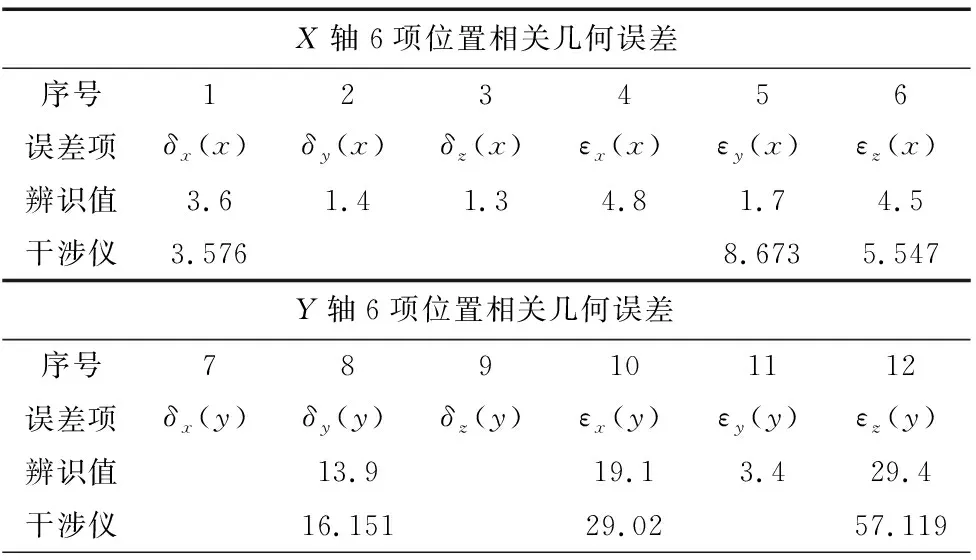
表4 数控机床的X、Y、Z轴几何误差和垂直度误差的测量和辨识结果

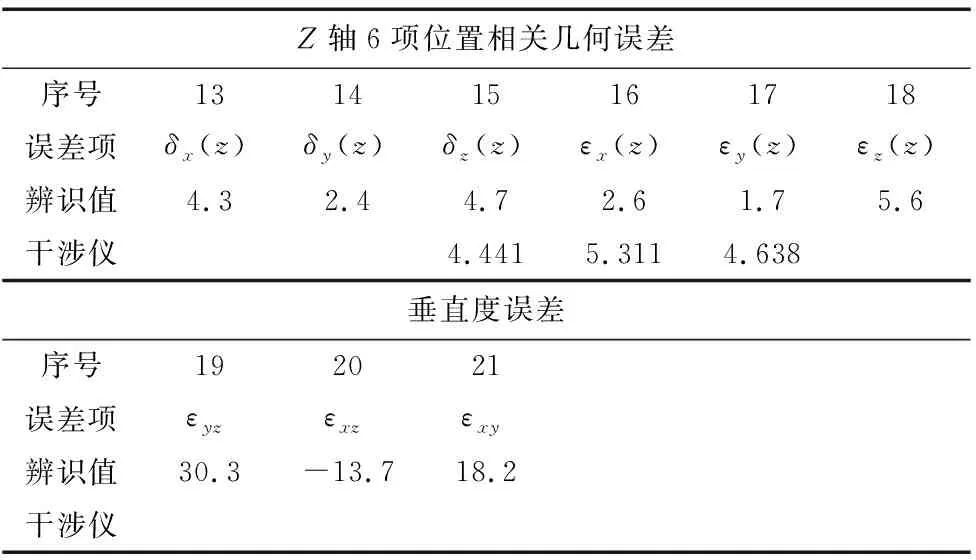
Z轴6项位置相关几何误差序号131415161718误差项δx(z)δy(z)δz(z)εx(z)εy(z)εz(z)辨识值4.32.44.72.61.75.6干涉仪4.4415.3114.638垂直度误差序号192021误差项εyzεxzεxy辨识值30.3-13.718.2干涉仪

Y坐标轴定位误差测量结果较大，主要原因是Y轴俯仰角和偏摆角较大引起Y轴定位误差随着Y坐标值增加而增大。

综合以上对比结果，关键几项几何误差辨识结果与干涉仪的测量结果误差值均较为接近，从而验证了前述辨识算法的正确性和有效性。

5 结论

通过系统研究数控机床几何误差的检测和辨识方法，得到了如下结论：

(1)引入一种多站分时测量方法，研究基于多边定位原理的数控机床刀具与工件相对位置误差的测量方法，该方法可以实现数控机床整个工作空间内测点误差标定，具有测量速度快，测量精度高等特点。

(2)提出了一种基于Laser TRACER 测量信息的几何误差快速辨识方法。该辨识算法可一次辨识得到数控机床的所有几何误差源，为机床的精度设计以及误差补偿奠定基础。

(3)引入一种基于两步解正则化方法的几何误差参数辨识方法，可以较大程度上提高误差参数辨识的抗干扰性和稳定性。

(4)对比实验验证了前述辨识算法的正确性和有效性。