基于运动轨迹误差最小化的平面四杆机构参数优化研究*

杨 帆，周丽红

(武汉科技大学城市学院，武汉 430083)

0 引言

连杆机构是机构学的主要研究对象，可以实现多种多样的运动，满足不同运动轨迹和位置的要求[1]。连杆机构的杆与杆之间通常采用低副连接，适合于高速重载[2]。连杆机构中最典型的是四杆机构，四杆机构因结构简单、容易加工和运动可靠等优点，广泛应用于化工、农业、海洋及航空领域。但是，四杆机构运动规律也变得越来越复杂，运动轨迹产生的误差也随之增大。因此，如何降低四杆机构运动轨迹误差，是当前研究四杆机构急需解决的问题之一。

当前，研究人员采用多种方法对四杆机构运动轨迹精度展开了研究。例如：文献[3]采用误差函数法研究了四杆机构运动轨迹的位置精度。针对四杆机构提出了修正距离误差函数，通过Matlab软件对轨迹误差进行了仿真，提高了运动轨迹精度，但是研究的等价因数不够全面，不具有代表性。文献[4]采用遗传算法研究了四杆机构运动轨迹所产生的误差，并且对运动轨迹误差进行了仿真，提高了运动轨迹精度，但是遗传算法搜索过程中，容易陷入局部最优解。文献[5]采用VC++研究了平面四杆机构运动轨迹的定位精度，通过复杂的数学模型和编程语言，实现了人机交互功能，操作简单可靠，提高了四杆机构运动轨迹精度，但是数学建模比较困难，还要学习复杂的编程语言程序。针对以上问题，本文采用改进粒子群算法研究四杆机构运动轨迹误差，不仅搜索最优解的速度快，而且运动精度高。创建平面四杆机构简图模型，根据数学几何关系式，推导运动轨迹点的平面坐标关系式。确定优化的设计变量参数，构造优化的误差函数，并且添加几何约束条件。采用改进粒子群算法优化四杆机构设计变量，优化后的四杆机构运动轨迹误差采用Matlab软件进行仿真，并且，与优化前的四杆机构运动轨迹误差形成对比，为深入研究四杆机构运动轨迹误差提供了理论依据。

1 四杆机构平面方程式

四杆机构在平面坐标系中简图及连杆参数如图1所示。

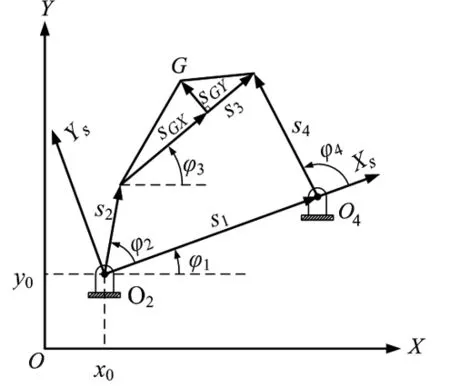
图1 四杆机构运动简图

在图1中，(x0，y0)表示四杆机构机架端点O2在平面坐标系中的位置，φ1表示机架旋转的角度，φ2表示输入杆运动的角度，G表示运动轨迹点，s1表示机架的长度，s2表示输入杆的长度，s3表示连接杆的长度，s4表示输出杆的长度，sGX和sGY表示运动轨迹点G的横向与纵向的长度，φ3表示连接杆s3运动的角度。根据图1可以写出机构各杆所构成的矢量封闭方程式[6]如下所示：

s2+s3-s4-s1=0

(1)

上式采用复数表示如下所示[6]：

s2eiφ2+s3eiφ3-s4eiφ4-s1eiφ1=0

(2)

假设φ1=0，方程式(2)的实部和虚部变换后如下所示：

(3)

公式(3)变换后可以得到：

(4)

求解方程式(4)得φ3、φ4如下所示：

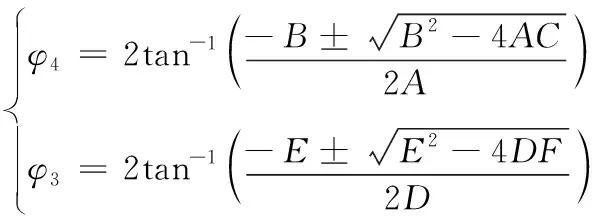
(5)

式中，A=cosφ2-K1-K2cosφ2+K3，B=E=-2sinφ2，C=K1- (K2+1)cosφ2+K3，D=cosφ2-K1+K4cosφ2+K5，F=K1+K5+(K4-1)cosφ2。

因此，运动轨迹点G在O-XY坐标系中横坐标和纵坐标方程式分别为：

(6)

式中，GXs=s2cosφ2+sGXcosφ3-sGYsinφ3，GYs=s2sinφ2+sGXsinφ3-sGYcosφ3。

2 误差函数

2.1 参数变量

四杆机构在运动过程中，G点的运动轨迹主要受以下参数的影响，分别为s1、s2、s3、s4、sGX、sGY、x0、y0、φ1和φ2。因此，设计变量选择以上10个参数进行优化，如下所示：

(7)

式中，φ2n表示φ2的n等份位置角度。

2.2 误差函数及约束条件

(8)

在没有限定的时间内，四杆机构不同的输入角度φ2i对应于不同的运动轨迹点Gi，实际运动轨迹点Gi通过输入角φ2i构成的集合如下所示：

(9)

因此，四杆机构运动轨迹点G的第一部分误差函数[7]如下所示：

(10)

式中，N表示运动轨迹点的数量。

四杆机构在运动过程中，必然会受到一些附加条件的约束，通过设置这些约束条件，从而推导出第二部分的误差函数。约束条件主要包括以下几个部分：

(1)根据格拉晓夫准则[8]，四杆机构存在曲柄的条件是至少有一个连杆能够做整周旋转运动，各个连杆的长度满足以下关系式：

(11)

(2)按照从小到大或从大到小排列输入角度φ2i，φ2i角度取值范围为[0,2π]。

(3)设计参数变量取值范围必须为正值。

根据以上两个部分，最终确定的误差函数如下所示：

(12)

式中，当四杆机构满足格拉晓夫准则时，h1(X)=0；当四杆机构不满足格拉晓夫准则时，h1(X)=1，输入角φ2满足排列序列时，h2(X)=0；输入角φ2不满足排列序列时，h2(X)=1；M1和M2表示惩罚误差函数约束因子。

3 改进粒子群算法

粒子群算法是一种仿生算法，主要是通过模拟鸟类的捕食过程，在N维空间中移动每个粒子，从而搜索到全局的最优值[9]。粒子群优化算法就是不断的更新极值点而实现最小值或最大值的只能算法。在粒子群算法中，关键是要平衡局部搜索能力和全局搜索能力。

在O-XY平面内，引入惯性权重ω来平衡局部搜索能力和全局搜索能力，粒子群的位置和速度计算公式如下所示[10]：

(13)

(14)

采用线性方式修改惯性权重系数，修改后的惯性权重如下所示：

(15)

式中,ωmax表示初始权重，ωmin表示最终权重，iter表示当前迭代数，itermax表示最大迭代数。

本文采用的改进粒子群算法是通过修改约束因子χ，使粒子速度vi+1=χ(vi)。修改后的约束因子可以增加粒子群算法的综合性能，约束因子的计算公式如下所示：

(16)

(17)

采用改进粒子群算法优化四杆机构运动轨迹误差的流程图如图2所示。

图2 四杆机构优化流程图

4 四杆机构误差仿真

四杆机构误差函数采用改进粒子群算法进行优化，初始参数设置如下：种群数量为100，种群最大迭代次数为500，交叉概率为0.85，变异概率为0.75，约束因子为0.72，κ=1.0，θ=4.1，c1=c2=2。四杆机构采用改进粒子群算法优化后的几何参数如表1所示。

G点实际运动轨迹误差采用Matlab软件进行仿真，G点横向和纵向的运动轨迹误差仿真结果分别如图4、图5所示。6个指定点的横向和纵向优化前后平均误差如表2所示。

表1 四杆机构几何参数优化结果

续表

图3 6个目标 运动轨迹点 图4 横向误差 仿真曲线 图5 纵向误差 仿真曲线

指定点优化前优化后单位横向平均误差0.4980.358mm纵向平均误差0.5920.325mm

由图4误差仿真曲线可知，优化前，四杆机构G点横向运动轨迹产生的最大误差值为1.0×10-3m；优化后，四杆机构G点横向运动轨迹产生的最大误差值为0.7×10-3m；G点产生的最大横向误差降低了30.0%。由图5误差仿真曲线可知，优化前，四杆机构G点纵向运动轨迹产生的最大误差值为0.9×10-3m；优化后，四杆机构G点纵向运动轨迹产生的最大误差值为0.5×10-3m；G点产生的最大纵向误差降低了44.4%。由表2可知，优化后横向平均相对误差降低了21.1%，优化后纵向平均相对误差降低了45.1%。因此，四杆机构几何参数采用改进粒子群算法进行优化，G点运动轨迹产生的横向和纵向误差较小，从而提高了四杆机构运动轨迹精度。

5 结束语

本文在二维坐标系中建立平面四杆机构运动简图，构造优化目标函数，引用改进粒子群算法优化平面四杆机构几何参数，将优化结果输入到Matlab软件中进行运动轨迹点误差仿真。仿真结果表明，优化后四杆机构运动轨迹点的横向和纵向平均误差降低，在相同条件下，纵向误差优化效果比横向误差更好，采用改进粒子群算法优化四杆机构几何参数，其运动轨迹定位精度更高，运动性能更好，提高了四杆机构运动的稳定性。