适用于T型输电线路的故障测距新方案

马 伟，侯伟宏，张 辉，章玮明，吴佳毅，丁 冬，林 森

（1.国网浙江省电力有限公司杭州供电公司，杭州 310009；2.国网浙江省电力有限公司，杭州 310007）

0 引言

T型输电线路具备输电走廊小、占地面积少、建设周期短、设备投资低等优势，在中压、高压和特高压等各级电网中应用日益增多[1-3]。输电线路作为电力系统中最易发生故障的元件，如何快速、准确地定位故障点，对保障电网安全、稳定、经济运行具有重要意义；同时，可减轻巡线压力，缩短故障恢复时间[4-6]。

目前，针对T型输电线路的故障测距主要包括行波法与故障分析法。

（1）行波法：捕捉故障点产生的暂态行波，利用其蕴含的故障特征来求解故障距离。如文献[7]以双端行波测距原理为基础，提出了基于改进互相关函数的故障测距方案；文献[8]通过推导故障发生的绝对时刻或行波波速，在判定故障支路后进而求取故障距离；文献[9]利用测量数据与线路参数的固有关系，建立以故障距离为未知量的线性方程组实现故障测距。

（2）故障分析法：建立线路故障分析模型，根据故障边界条件构造测距方程。文献[10]利用电压相位会在故障点突变的特点，通过遍历搜索法求取故障位置；文献[11-12]利用健康支路电气量折算得到T接点电压和电流，再结合故障支路母线侧电气量实现双端测距；文献[13]利用三侧母线处故障相依次跳闸产生的多时刻断面信息，构造了单端阻抗测距方案。

图2 等值网络

行波测距精度高，但需要专用设备且技术较为复杂。而故障分析法对设备要求低、易于实现，在实际电网中应用广泛[12]。鉴于此，本文提出了一种基于故障稳态电流的T型输电线路故障测距新方案。首先，通过对故障支路列写局部节点电压方程，推导出T型输电线路的故障稳态等值网络；然后，利用任意两端母线保护安装处的故障稳态电流，建立以故障位置为未知量的方程；最后，采用叠加原理求取故障稳态电流，实现故障测距功能。仿真结果验证了本方案的正确性与有效性。

1 基本原理

以图1所示的T型输电线路为例，O点为T接点，母线M侧、N侧和S侧系统电压分别为其等值阻抗分别为 ZM，ZN与 ZS。

图1 T型输电线路模型

1.1 故障稳态电流

若不计及电力电子等非线性元件，电力系统可视为线性网络。根据叠加原理，故障状态可由正常状态、故障暂态和故障稳态3部分构成[14-15]。其中，正常状态指故障前运行状态；故障暂态指节点注入电流（电源提供电流与负荷电流之和，且以流入母线为正方向）变化引起的暂态过程；故障稳态指仅由故障点电压引起的状态。以MO支路故障为例，故障暂态网络如图2（a）所示，其中分别表示母线M侧、N侧和S侧节点注入电流变化量；故障稳态网络如图2（b）所示，其中表示故障点电压。

依据电力系统网络理论知识，在正常状态网络中，节点注入电流与保护安装处电流之间存在关系[14]：

同理，在故障暂态网络中，节点注入电流与保护安装处电流之间存在如下关系：

因此，根据故障后电流、正常状态电流与故障暂态电流，可求得故障稳态网络中支路MO，NO与SO保护安装处的电流为[16]：

1.2 测距方案

对故障支路NO列写局部节点电压方程：

根据式（5）可知，T型输电线路的故障稳态等值网络如图4所示。

可以看出，故障稳态等值拓扑结构与正常状态网络相同，只是将故障点电流依照故障点位置分配到支路两端。因此，在故障稳态等值网络中，仅在支路NO的母线节点处存在注入电流，即故障稳态网络中保护安装处的电流为：

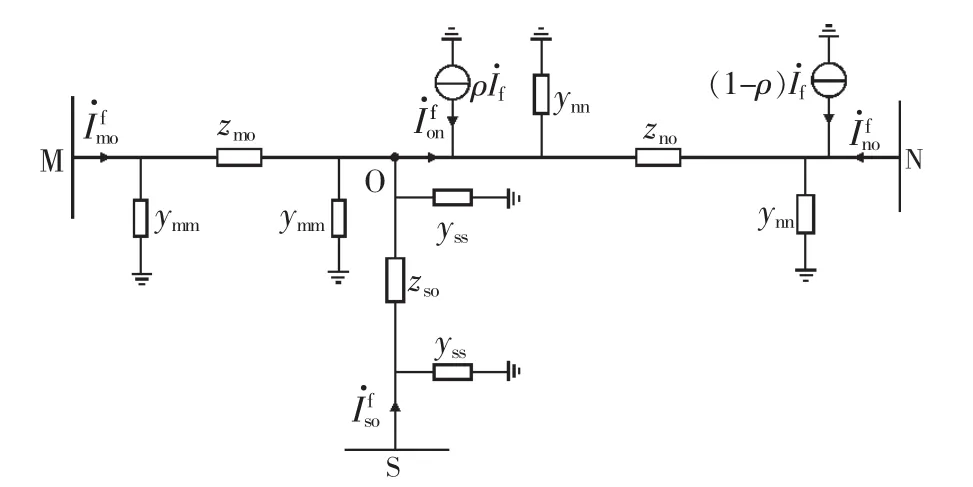
图4 NO支路故障时故障稳态等值网络

依据式（6）可知，M侧与N侧电流间存在以下关系：

同理，利用M侧与S侧电流求取故障距离百分比：

理论上，式（8）—（10）的计算结果应完全一致。但计及采样等误差因素，故障距离百分比宜取式（8）—（10）的平均值。

因此，故障点到母线的故障距离D为：

式中：l表示支路长度。

上述分析亦适用于MO支路与SO支路故障，限于篇幅不再赘述。对于故障支路的辨别，本文采用现有故障测距方案中普遍使用的电压法[13]：借助母线侧电气量信息分别计算T接点的电压，然后利用故障支路与另外2个健康支路计算电压不相等的特点来判断故障支路。

此外，由式（3）可知，故障稳态电流可根据故障后保护安装处的测量电流与母线处节点注入电流求取，因此，本方案在短路故障后一直投入。

2 仿真验证

为验证本方案的正确性与有效性，基于PSCAD/EMTDC软件平台搭建图5所示系统。故障点f1，f2，f3分别位于支路B1T，B2T与B3T上。

图5 仿真模型

（1）系统参数

（2）线路参数为：

支路 B1T：l=100 km，R1=0.029Ω/km，X1=0.362Ω/km，C1=0.014μF/km；R0=0.255Ω/km，X0=0.971Ω/km，C0=0.009μF/km。

支路 B2T：l=80 km，R1=0.030Ω/km，X1=0.278Ω/km，C1=0.013μF/km；R0=0.278Ω/km，X0=0.652Ω/km，C0=0.006μF/km。

支路 B3T：l=70 km，R1=0.027Ω/km，X1=0.278Ω/km，C1=0.011μF/km；R0=0.194Ω/km，X0=0.642Ω/km，C0=0.09μF/km。

支路 B2B3：l=35 km，R1=0.021Ω/km，X1=0.280Ω/km，C1=0.012μF/km；R0=0.115Ω/km，X0=0.719Ω/km，C0=0.005μF/km。

在仿真过程中，采用全周傅氏算法提取电流量，采样频率为2 000 Hz，故障发生时刻为0.4 s，并利用0.46 s的采样数据进行故障测距。

2.1 故障类型

当故障点f2距母线B2为40 km处发生不同类型故障时，仿真结果见图6。其中，实线、短虚线与长虚线分别表示式（8）—（10）的计算结果。

可以看出，不论发生何种类型故障，利用式（8）—（10）均能够快速、正确地计算得到故障距离，且精度高。

当故障点 f1，f2，f3分别距母线 B1，B2，B3为30 km处发生不同类型故障时，故障测距结果如表1所示。可以看出，本方案不受故障类型的影响，在不同情况下均能够准确地计算故障距离。最大误差出现在故障点f1处发生三相短路情况下，其值为-0.460 2%。

图6 距母线B2为40 km处发生不同类型故障时仿真结果

2.2 故障位置

当故障点 f1，f2，f3分别距母线 B1，B2，B3不同位置发生不同类型故障时，故障测距仿真误差如图7所示。其中，单相接地故障时过渡电阻为100Ω，两相接地故障时过渡电阻为50Ω。可以看出，本方案不受故障位置的影响，不论在线路上发生何种类型故障，均能够较准确地计算故障距离。其中，支路B1T发生故障时，最大误差出现在故障点f1距母线B1为100 km处发生A相接地情况下，其值为2.033 8%；支路B2T发生故障时，最大误差出现在母线B2出口处发生AC接地情况下，其值为1.923 4%；支路B3T发生故障时，最大误差出现在母线B3出口处发生AC接地情况下，其值为2.280 7%。

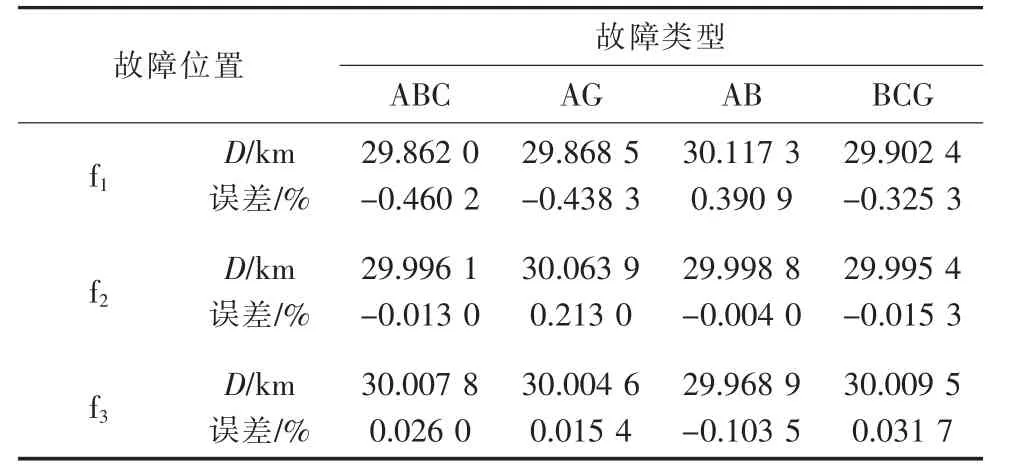
表1 不同类型故障的仿真结果

图7 在不同位置发生故障时测距误差

2.3 过渡电阻

当故障点 f1， f2， f3分别距母线 B1， B2， B3不同位置经不同过渡电阻发生单相接地故障时，故障测距仿真误差如图8所示。

图8 经不同过渡电阻发生故障时测距误差

可以看出，不论在线路上何处发生故障，本方案故障测距结果均不受过渡电阻的影响。其中，支路B1T发生故障时，最大误差出现在故障点f1距母线B1为90 km处经300Ω过渡电阻发生故障情况下，其值为-2.621 4%；支路B2T发生故障时，最大误差出现在故障点f2距母线B2为40 km处经300Ω过渡电阻发生故障情况下，其值为1.554 6%；支路B3T故障时，最大误差出现在故障点f3距母线B3为50 km处经300Ω过渡电阻发生故障情况下，其值为2.193 7%。

2.4 负荷电流

系统电压的相角能够反映线路负荷状态，负荷电流始终由电压超前侧流向滞后侧，且相角差越大，线路负荷越重[17]。在不同负荷状态下，故障点 f1， f2， f3分别距母线 B1， B2， B3为 30 km 处发生不同类型故障时，故障测距仿真结果如表2所示。其中，方式1中S1系统参数为U=500∠-10°kV，S2系统参数为U=500∠20°kV，S3系统参数为U=500∠5°kV； 方式 2 中 S1系统参数为 U=500∠5°kV， S2系统参数为U=500∠-10°kV，S3系统参数为U=500∠15°kV。

表2 不同负荷状态的仿真结果

可以看出，本方案不受负荷电流的影响，不论发生何种类型故障，均能够正确计算故障位置，且精度高。在2种不同运行方式下，最大误差均出现在故障点f1发生单相接地故障情况下，其值分别为-0.945 9%与-0.734 7%。

3 结语

通过推导T型输电网络的故障稳态等值网络，利用任意两端母线保护安装处的故障稳态电流，建立以故障距离为未知量的方程。在此基础上，提出了适用于T型输电线路的故障测距新方案。仿真结果表明，该方案不受故障类型、故障位置、过渡电阻和负荷电流等影响，在线路发生故障后能够实现快速、准确地故障测距。

需指出的是，随着新能源大规模并网，多分支输电线路在电力系统中不断涌现，下一步研究重点是适用于多点T接输电线路的故障测距方案。