一类可化为爪型的高阶行列式计算方法

武慧虹 钱淑渠

(1、2.安顺学院数理学院，贵州 安顺561000)

行列式在很多科学和工程问题中具有广泛的应用，如线性系统的求解[1]，雅克比行列式计算及工程电路设计的符号分析[2]。低阶行列式的计算有通用的标准计算方法，高阶行列式的标准计算方法只能根据行列式的定义将其按行或列展开并分解为多个低阶的行列式，再逐步降维交替操作获得最终结果[3]，该方法虽然仅涉及简单的“加、减、乘”运算，但随着行列式阶数的增大，其计算量呈阶数的阶乘级上升。此外，借助行列式的基本性质及矩阵的初等变换，将高阶行列式化为上(下)三角形行列式也是一种规律性较强的高阶行列式的计算方法[4]，但该方法需要初等变换来避免零元素作为主元出现的情况，故存在一定的局限。实际上，对于某些特殊类型的高阶行列式，采用上述一般性方法计算其运算过程极其复杂且易于产生计算错误，但若研究行列式本身的特征，妙用某些技巧将会产生事半功倍的效果。为此，文章针对一类具有一定特征的高阶行列式，研究爪型行列式在其计算中的妙用，以提高数学/非数学专业学生学习这类高阶行列式的计算效率，增加他们学习代数学的兴趣，对高阶行列计算的教学提供一定的实用价值。

1 爪型行列式定义及计算方法

1.1 定义：形如

的行列式称为爪型行列式[5,6]，其中bj≠0,j=1,2,…,n。

爪型行列式的基本特征是：

(1)两条边线上的元素不全为零，对角线位置b1,b2,…,bn均为非零；

(2)除(1)规定外，行列式其余位置元素均为零。

1.2 爪型行列式的计算方法

爪型行列式由于具有类似如手爪，其计算方法具有一定的规律和技巧，主要是利用对角线上的元素消去“横线”或“竖线”上的非零元素，将原行列式化为三角形行列式再进行计算，具体如下：

计算机技能培训平台的设计研究以旧州镇农村劳动力应用为例” 设有如下爪型行列式，则根据行列式的性质作如下计算：

(1)

(2)

上述计算过程采用了分别以第j(j=2,3,…,n+1)列乘以常数-ej-1/bj-1加到第1列，将第1列e1,e2,…,en位置消为零，则原行列式等价变换为上三角行列式，从而易于计算等价行列式的值。当然也可以采用分别以第i(i=2,3,…,n)行乘以常数-ai-1/bi-1加到第1行而计算。

注：其他类型的爪型行列式计算请读者自己思考，这里不再赘述。

2 爪型行列式的妙用

爪型行列式妙用于高阶行列式的计算，可为基础差的数学/非数学专业学生提供极易掌握某些特殊高阶行列式的计算方法。本部分通过具体实例研究爪型行列式如何妙用于高阶行列式的计算。一般而言，需要考察待求行列式的特征，若待求行列式除对角线元素外，其余各列(行)元素均分别相同，则该行列式可运用行列式的性质等价变换为爪型行列式，从而借助爪型行列式的计算公式极易获得结果，下面以例2.1、2.2和2.3给予实例介绍。

例2.1：计算阶行列式

分析：高阶行列式除了对角线元为外，各列其余元素均为，根据前面所述，可等价变换为爪型行列式。以下给出两种等价变换解法：

解法一：直接化为爪型

因为

(3)

观察式(3)易知其为爪型行列式。与式(1)对比可知d=x,aj=a,bj=x-a,ej=a-x，代入公式(2)可得：

解法二：加边法化为爪型

因为

(4)

观察式(4)易知其为爪型行列式，与式(1)对比可知d=1，aj=a,bj=x-a,ej=-1代入公式(2)可得：

评注：由上述两种解法易知，满足可化为爪型行列式的高价行列式，经ri+kr1变换后，原行列式即可变为爪型行列式，从而利用爪型行列式公式直接得出结果。

例2.2：计算n阶行列式

解析：由高阶行列式Dn的各列特征，易知其可采用直接法化为爪型行列式。

因为

(5)

观察式(5)可知其为爪型行列式。与式(1)对比可知d=a+x,aj=a,bj=x,ej=-x，代入公式(2)可得

评注：本题如同例1也可采用“加边法”将原行列式化为爪型行列式，此题的另一种变形形式为：

读者可按本例易于求解得

例2.3：计算n阶行列式

解析：同理，由于高阶行列式Dn中除对角线元素外，各列其余元素都分别相同，考虑添加一行一列，将相同的元素化为0，使计算简化。

因为

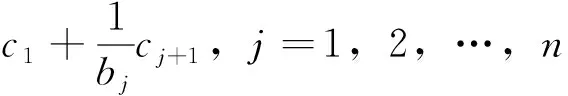
评注：上述计算方法采用了“加边法”将原行列式化为爪型行列式，实际上也可直接将其变换为爪型行列式，请读者自己练习。

3 结论

文章首先给出了爪型行列式的定义及其计算，然后针对一类具有一定特征的高阶行列式，通过具体实例介绍了采用“直接法”和“加边法”将其化为爪型行列式，最后采用爪型行列式的计算公式直接获得高阶行列式的值。该方法解决了数学/非数学专业学生求解这类高阶行列式计算困难的问题，为本部分的教学和学习提供了一种高效快速的计算方法。