基于电负性均衡理论快速计算多肽分子中原子电荷的新方法

欧阳永中，花书贵，邓金连

1佛山科学技术学院 环境与化学工程学院，广东 佛山 528000

2江苏第二师范学院生命科学与化学化工学院，江苏省生物功能分子重点建设实验室，南京 210013

1 Introduction

The concept of atomic charge is fundamental to chemistry as it gives powerful insights towards the understanding and predicting of chemical reactivity and physical properties, such as dipole moments, interpret solvation properties, hydrogen bonding, molecular reactivity1, etc. Electrostatic interactions,derived from atomic charges, have played a crucial role in molecular mechanics and dynamics simulations of large biological molecules2and understanding many complex processes, such as transitions between stable protein conformers3,protein folding4, ligand docking5, and so on. Unfortunately,there is no clear definition of the concept of atomic charge until now. As such, various definitions or algorithms to estimate the values of atomic charges have been devised. The most commonly used approaches are the ab initio molecular orbitalbased methods such as Mulliken population analysis (MPA)6,Lӧwdin population analysis7, and natural population analyses(NPA)8, which define atomic charges by assigning the electrons to the atom where the orbital is centered. An alternative approach for obtaining atomic charges is to make use of the charge distribution to obtain atomic charges, termed Hirshfeld-I scheme9.Instead, charges can also be derived by fitting the electrostatic potential (CHELPG)10to point charges or making use of the atomic polar tensors (GAPT)11.

A theoretically sound to the atomic charge definition is the Bader’s Quantum Theory of Atoms-In-Molecules (QTAIM),which partitions a molecular structure into submolecular regions by the zero-flux surfaces of gradient electron density Δρ(r) and derives atomic populations by integral of the electron density within the atomic basins12–14. Instead of determining the charge of an atom by counting the number of electrons in the orbital centered on the atom, it counts the electrons in a region of real physical space of the atomic basins. Thus, the well-defined atomic basins which obey the virial theorem have strong physical significance. Many molecular properties such as Atoms-In-Molecules (AIM) charges are based on the welldefined atomic segments of the electronic charge density and can be derived from an experiment (via X-ray diffraction experiments)15–17. Compared to other population analysis, the QTAIM method rests on the firmest theoretical grounds and shows a significant meaning in experiments18. Although these quantum chemical calculations have successfully been applied to describe the atomic charge distributions in small molecular systems, they are extremely time demanding for biomolecules.Particularly for AIM charges derived process, much greater computational cost is needed when performing the necessary three-dimensional integration within the atomic basin, as comparison to other atomic charge schemes (such as MPA,NPA, etc.). Thus, an alternative approach for calculation of atomic charges accurately and economically is desirable.

Most empirical approaches that only require less computational effort have been developed for fast computation of atomic partial charges in large molecules. These approaches are mainly based on the principle of the electronegativity equalization formulated by Sanderson19, such as the partial equalization of orbital electronegativity (PEOE)20, the charge equilibrium approach (QEq)21, the electronic populationderived atomic charges (EPAC) method22, split-charge equilibration (SQE)23, etc. The electronegativity equalization method (EEM)24developed by Mortier et al., is a typical formalism to implement this principle. Later, Bultinck et al. have parameterized and validated the EEM method mainly for small organic molecules and some drug-like compounds, using different Atomic Charge Schemes25,26. To include the bond nature, the atom-bond electronegativity equalization method(ABEEM)27,28, developed by Yang et al., has been successfully applied to predict the atomic charge distribution for large organic molecules in aqueous solution, even metallobiomolecules29.Meanwhile, a modified EEM method, which considers the effect of atom connectivity and hybridization, has been devised to improve the accuracy of EEM method by Ouyang et al.30.Recently, the EEM model has been parameterized for proteins using different population analysis (e.g., Mulliken, natural,Hirshfeld, Hirshfeld-I), without involving any chemical environments31,32.

However, atomic charge distributions in a molecule are both connectivity27,30and geometry-dependent33–35. This means that atoms of a given type with the same hybridized states and connectivity but in different fragments or functional groups should be assigned to different parameters in the EEM calibration, because that they have different local molecular environments resulting from the surrounding atoms to which are indirectly connected (e.g., weak bond interactions from hydrogen bonds). Actually, the effect of the local chemical environments in fragments or groups on the atomic charge distributions in a molecule has been verified by the remarkable transferability of atomic charges of the main chain fragments or functional groups common to the amino acids and polypeptides36–43, and hence can not be neglected in the EEM calibration, but none of these previous studies mentioned above has considered the effect of local molecular environments in the EEM calibrations.

One most important aspect of the QTAIM theory is the high degree transferability of submolecular properties (e.g., atomic charges and volumes). This means that very reproducible atomic properties for the contributing atoms can be derived if the chemical environment is comparable. For macromolecules such as polypeptide and proteins, one can use its constituted fragments or functional groups as building blocks for the additive generation of the electronic densities of macromolecules. In the present study, a novel efficient approach,based on the Bader’s concept of high degree fragment transferability of atomic charges14,39,40,43, has been proposed for parameterization of atomic-charge parameters of EEM for polypeptides or proteins. Not only the factors of connectivity and hybridized states, but also the effect of local chemical environments in fragments or groups has been taken into account in the EEM parameterization. The main peptide group (NH―HαCα―C＝O) of polypeptide in the backbone was used as the building blocks to model EEM parameters for reproducing atomic charges in polypeptides. A training set of 20 terminally blocked occurring amino acids (Ac-X-NHMe, X = any neutral residue) that recreate the immediate local environment of the main chain fragments or functional groups of polypeptides were chosen for the calibration of AIM charges using the Differential Evolution algorithm. As a result, the most time-consuming derived AIM charges for polypeptides or proteins can be rapidly and accurately reproduced using the EEM parameters calibrated in this work, providing a new scheme for parameterization of EEM method for large systems which possess highly repeated segments such as polypeptides or polynucleotides.

2 Methods

2.1 Electronegativity equalization method

The electronegativity equalization principle proposed by Sanderson19states that when two or more atoms combine to form a molecule, effective electronegativity (χi) of every atom is equal to the molecular electronegativity χeq:

The effective electronegativity of the ith atom in the molecule can be given by Eq. (2):

where N is the number of atoms in the molecule, qiand qjare the net charges distributed on the atoms i and j, respectively, Rijrepresents the interatomic distance between atoms i and j. The χ*i andwhich are the effective atomic electronegativity and hardness of ith atom in the molecule, respectively, are defined by Eq. (3).

For an arbitrary molecule with N number atoms, one has(N + 1) unknown quantities (N-atomic charges of qiand one value of χeq), When Eq. (1) is applied to each atom, it can simultaneously yield N linear equations. These equations along with Eq. (4) can be combined into N + 1 linear equations, which can be expressed in matrix form as:

It can be seen from Eq. (5) that once the parametersandare given, the atomic charges could be calculated at high speed using the above matrix algebra.

2.2 Selecting training and test sets

In the context of molecular modeling, the higher similarity degree of the training sets to the model systems is, the closer the simulated results is to the reality44. One most important aspect of the QTAIM theory is the high degree transferability of submolecular properties (e.g., atomic charges and volumes),meaning that for macromolecules such as polypeptide and proteins, one can use its constituted fragments or functional groups as building blocks for the additive generation of the electronic densities of macromolecules36–43.

As shown in Fig. 1, each structure of polypeptides can be divided into many pieces of fragments, which consist of a single residue each. Thus, a large number of terminally blocked amino acids (Ac-X-NHMe, X = any neutral residue) which furthest reflect the local chemical environments within the polypeptides were chosen as a training set for modeling EEM parameters for polypeptides in this study (see Fig. 2). Because huge computational resource are demanding for deriving AIM charges by quantum mechanical calculations, only the representative structure of Ac-X-NHMe for each amino acid residue were considered. As a result, a training set of dipeptides of 20 naturally occurring amino acids (Ac-X-NHMe, X = any neutral residue) containing C, N, O, H, and S elements are calibrated in the EEM parametered process.

The initial conformations for each amino acid residue were taken from the local minima for Ac-X-NHMe (X = 20 any neutral residue) optimized by the ECEPP/2 and ECEPP/2 force fields45, which has the largest boltzman probability of all minimum-energy conformations. Further geometry optimizations were carried out at the B3LYP/6-31G+(d,p) level of density functional theory (DFT) theory for those initial conformations, and the lowest energy structure for each residue was finally selected as training set. For two test tetrapeptides of Ac-GASA-NHMe and Ac-YGFM-NHMe, their initial representative conformations both were directly taken from the peptide Atlas conference database (http://www.peptideatlas.org)published by NIST, followed by further geometry optimization using the B3LYP/6-31+G(d,p) method.

Fig. 1 The terminally blocked form of tetrapeptides of CH3CO-Gly-Ala-Ser-Ala-NHCH3 (Ac-GASA- NHMe).

Fig. 2 The terminally blocked form of dipeptides of the naturally occurring amino acid Ac-X-NHCH3 (X = 20 any neutral amino acid residues).

2.3 Defining atom types

The empirical parameters needed to be calibrated in the EEM model are associated with free atoms (andand their corrections (Δχiand Δηi). The corrections to the free-atom electronegativity are actually invoked by the change in size and shape of the atom in the molecule, as well as the chemical environments from the surrounding molecules24. In previous EEM calibrations24–32, atom types are usually defined according to the atom type, bond type, and hybridized states, as well as atoms that bonded to, and hence assigning different set of parameters for each atom type. However, atomic charge distributions in a molecule are both connectivity27,30and geometry-dependent33–35. Actually, the effect of the local chemical environments in fragments or groups on the atomic charge distributions has been verified by the remarkable transferability of atomic charges of the main chain fragments or functional groups common to the amino acids and polypeptides36–43, and hence can not be neglected in the EEM calibration. This means that atoms with the same valence states and connectivity but in different fragments or groups actually carry different charges, and thus should assign different parameters (as shown in Fig. 3). That is, atom type recognitions and definition should depend on not only the atom type,hybridized states and all atoms to which it directly bonded, but also the molecular environments from the surrounding atoms to which are indirectly connected.

Fig. 3 An example of threonine is to show that atoms with the same connectivity and hybridized states but in different local chemical environments have different atomic charges from quantum mechanical calculations (in electron units).Geometry optimization and wave functions calculations were carried out using the RB3LYP/6-31+G(d,p) methods. The atomic population N(Ω) is obtained by the integration of the electron density over the basin of the atom. The atomic charge is the sum of the nuclear and electronic charges, q(Ω) = Z(Ω) - N(Ω).

Table 1 Optimized Values of χ＊ and η＊ for each atom type with including the effect of the local chemical environments in fragments or functional groups a.

To consider the effect of chemical environments in a local region, one should make sure which submolecular fragments or functional groups each atom belongs to. The main peptide group(NH―HαCα―C＝O) and carboxyl group (COOH), which is a key component of polypeptide in the backbone and side chain,respectively, were both used as two building blocks to model EEM parameters for reproducing atomic charges in polypeptides.Each atom in the peptide group (NH―HαCα―C＝O) and carboxyl group (COOH) is considered as an atom type, leading to a total of 36 sets of effective electronegativity and hardness parameters of atom types involved C, H, O, N, and S (as shown in Table 1). Except the Gly residue, the Cβatom directly connected to the Cα carbon can also regarded as a part of peptide group and should be distinguished from other carbons, since great deviations of AIM charges from other carbon types was found for Cβ atom. Only the S atom still keeps one atom type in the calibration. However, given the choice of side-chains in the peptides used for benchmarking there are several atom types(notably non-amide N and COOH) that are not tested against the model presented in this study.

For a given atom type, with a set of parametersand,contains not only the atom symbol, valence states, and connectivity but also the information about its local environments in different functional groups. All these information are extracted automatically from the .mol2 files using a program developed by our group, and the .mol2 files are convert from the .out files produced by the Gaussian 03.

2.4 Quantum mechanical calculations

All chosen training sets and two test molecules (Ac-GASANHMe and Ac-YGFM-NHMe), obtained from the force fields mentioned above, were further optimized at the B3LYP/6-31+G(d,p) level of DFT theory using the Gaussian 03 program46.The ab initio AIM charges calculated at the same level using the AIM2000 program were denoted as DFT-AIM, and the AIM charges calculated from EEM method will be expressed as EEMAIM. This basis set contains the diffuse functions required to describe weak hydrogen bonding interactions. It should be noted that the wave funcation files (.wfn) used for calculating AIM charges by the AIM 2000 program47were firstly generated using the Gaussian 03 program.

2.5 Calibration of atomic-charge parameters

The effective electronegativity and hardness for AIM charges containing C, H, O, N, and F elements without including any chemical environments have been calibrated in simplex method and genetic algorithm by Bultink et al.26. The new scheme proposed in this study for calibration of EEM method differs from the original EEM26method in three ways. First, not only the factors of connectivity and hybridization states, but also the local chemical environments in different fragments or functional groups which influence the atomic charges distribution are considered in this scheme. Second, instead of adjusting the effective electronegativity of H to 1.0 eV in the optimization, no restrictions were imposed on any of calibrated parameters.Finally, the differential evolution (DE) algorithm employed for optimization in the present study48can produce better results than those from the genetic algorithm used in the original EEM method26.

Instead of using the same parameters for the same element,there are 6 and 4 different sets of effective electronegativity and hardness values for the peptide group (NH―HαCα―C＝O) and carboxyl group (COOH), respectively, and only the sulfur remains the one atom type, leading to a set of 36 parameters in the optimization (Table 1). To reasonably determine the specific sets of 36 parameters, the 36 parameters are firstly assigned randomly, and then are applied to calculate EEM charges for all atomic types by Eq. (5). Each set of parameters is evaluated using the fitness function of Eq. (6) in comparison with corresponding DFT charges, and is optimized by the DE algorithm.

where i refers to a specific atom type for C, H, O, N, and S elements with different chemical environments, j to a molecule from the training sets, and k to a certain atom type i in molecule j. M is the number of molecules, and Njiis the number of a specific atom type i in molecule j. L is the total number of atom types (L = 18 in this case), and the total number of a specific atom type i over all molecules is denoted Ni.

3 Results and discussion

The calibration of AIM charges parameters in the EEM has proved to be a highly cumbersome task25,26,30. In addition to the sensitivity of the fitness function for the parameters, the quality of the calibrated parameters has proved to be dependent on not only the factors of connectivity and hybridized states, but also the ability of the optimization method30. In this study, the effect of chemical environments in a local region is found to be another most import factor which should be taken into account for deriving atomic AIM charge parameters. This means that atoms with the same valence states and connectivity but in different fragments or groups with different chemical environments should have different parameters. Besides, the extremely computational resource required to quantum mechanically deriving AIM charges of a large set of 20 dipeptides training molecules and two test tetrapeptides (Ac-YGFM-NHCH3and Ac-GASA-NHCH3), makes the calibrated parameters much more useful in the fast calculation of AIM charges.

3.1 The effect of local chemical environments

Fig. 3 gives the AIM charge distributions in the threonine molecule, of which geometry optimization and quantum mechanical calculation of AIM charges were performed using the B3LYP/6-31+G(d,p) method. It is evident that the connectivity and hybridized states are still the two major factors to affect the atomic AIM charge distributions, which are in good agreement with previous studies for calibrating Mulliken and NPA charges25,26,30. The same hydrogen element attached to different atoms has different atomic charges, and large differences of AIM charges were found for the hydrogen atoms that bonded to C, O and N atoms, respectively. Similar instances also occur in all 20 training sets of molecules. This is mainly attributed to the large discrepancies of electronegativity between hydrogen and its connected atoms, leading to the result that a larger number of electrons around the atom with relatively lower electronegativity have been attracted by its connected atom, and hence reducing the value of atomic charges.

However, atomic charges in a molecule are geometrydependent33–35. From the Fig. 3, it can be found that the atomic charge for oxygen atom in the hydroxyl group (q = -1.119e) is different from that in the carboxyl group (q = -1.160e), although they have the same connectivity and hybridized states. The similar conditions also occur for the hydrogen element that AIM charges for the hydrogen atom in the hydroxyl group (q =0.572e) has obvious deviations from that in the carboxyl group(q = 0.611e), because of different local chemical environments which they belong to, respectively. In fact, different molecular environments for different functional groups are resulted from the surrounding atoms to which are indirectly connected (e.g.,weak bond interactions from hydrogen bonds).

As already mentioned, one most aspect of the Bader’s theory is the transferability of submolecular properties14,39–43. To further examine the degree of transferability of atomic charges in the peptide bond region, the atomic charges for the 20 dipeptides of terminally blocked amino acids (Ac-X-NHCH3, X = any amino acid residue) and pentapeptides of Boc-Gln-D-Iva-Hyp-Ala-Phol(Boc, butoxycarbonyl； Gln, glutamine； Iva, isovaline； Hyp,hydroxyproline； Ala, ethylalanine； Phol, phenylalaninol) are calculated and summarized in Fig. 4. The average AIM charges agree well within the given atom types by 0.01e–0.04e, which is a surprisingly small spread. The Hα atoms carry a small positive charge, the Cα atoms and hydrogens of the peptide NH group are moderately positively charged, and the C’ atoms carry a high positive charge, whereas strong negative charges more than 1e are obtained on the N and O atoms. The positive charges on the Cα,C’, Hα and H atoms total approximately +2.4e and the negative charges on N and O amount to about -2.42e, so for each peptide bond region an excess of -0.02e must be compensated by the sidechains. Very reproducible AIM charges for the atoms in peptide bonds of these amino acid residues and oligopeptides, (in Fig. 4)further verified the perfect fragment transferability of atomic charges, indicating that the effect of the local chemical environments in fragments or groups on the atomic charge distributions is obvious for these main chain fragments or functional groups common to the amino acids and polypeptides,and thus can not be neglected in the EEM calibration for polypeptides or proteins36–43.

Therefore, the main peptide group (NH―HαCα―C＝O) was used as the building blocks to model EEM parameters for reproducing atomic charges in polypeptides, based on the Bader’s concept of fragment transferability of atomic charges.Each atom in the peptide group (NH―HαCα―C＝O) is distinguished from that in the side chain or other fragments and should be regarded as an individual atom type in the EEM calibration, even though they may have the same valence states and connectivity. This means that atoms of a given atom type in a molecule with the same connectivity and hybridized states, but in different chemical submolecular fragments or groups actually carries different charges and hence should have different parameters. This is because that the molecular environments for a given atom type in a molecule are influenced not only by the atoms to which it bonded directly, but also by the atoms from the surrounding atoms to which it can not be directly connected.Besides, the carboxyl group (COOH) is the major functional group in the side chain of polypeptides, each atom of which should also be assigned to different parameters from other atoms due to the different chemical environments in the COOH from other groups. Thus, the final atom type definitions used for polypeptides modeling are shown in Table 1.

Fig. 4 Average calculated atomic AIM charges (e) of the atoms in the peptide bond region.A refers to twenty dipeptides of terminally blocked amino acids(CH3CO―NH―CH(R)―C=O―NHCH3)； B refers to the pentapeptide Boc-Gln-D-Iva-Hyp-Ala-Phol (Boc, butoxycarbonyl； Gln, glutamine； Iva, isovaline；Hyp, hydroxyproline； Ala, ethylalanine； Phol, phenylalaninol) 36； av is the average over all entries. n is the number of contributing entries. The estimatedstandard deviation of the mean is given in parentheses.

3.2 Influence of optimized method

Although the quality of the calibrated parameters is affected to a great extent by the chemical environments included in the training sets, the process for the choice of optimized method suitable for the objective function is also one of the most crucial steps in the calibration30. This is because that the ability of the optimized method directly determines the quality of the optimized parameters, especially when involving large amounts of variables. Generally, an efficient optimization approach should fulfill the following three requirements. First, the method can locate the true global minimum, regardless of the initial system parameter values given； Second, convergence should be fast； Finally, the program should has a minimum of controllable parameters so that it will be easy to use. The Differential evolution (DE) algorithm48，which has proved to be a powerful approach for minimizing nonlinear and non-differentiable continual space functions and has shown to be superior to several other optimized methods, has been applied to the this study.

To test whether it is suitable for the calibration of AIM charges parameters for the objective function, Fig. 5 shows the comparison of the convergence efficiency of three commonly used optimized algorithms, including Accelerated Random Search algorithms (ARS)49, Particle Swarm Optimization algorithms (PSO)50and Differential Evolution algorithms (DE)for the objective function Eq. (6), respectively. It is clear that DE algorithm converges much faster, and after 10000 iterations, the achieved minimum value is much smaller compared to those of PSO and ARS algorithms (the minimum values for PSO, ARS,and DE are 0.331, 0.051, and 0.0184, respectively), although the global minimum cannot be confirmed for the minimum objective function value obtained by DE algorithms. This may be mainly due to the high sensitivity of the fitness function with respect to the calibrated parameters and it is more likely to end up in local minima. However, what can be assured is that the global minimum value is remarkably easy to obtain for DE algorithms.At least for the objection function (6) in this study the DE algorithm is regarded as the best choice compared to other algorithms.

Fig. 5 Comparison of the efficiency of convergence for different optimization algorithms.ARS, PSO, and DE represent Accelerated Random Search, Particle Swarm Optimization, and Differential Evolution algorithms, respectively.

3.3 Quality of the EEM-AIM charges

The quality of the AIM charges obtained from the EEM method described in this work is evaluated by comparison with the results from quantum chemical calculations. To test whether and how much the accuracy of EEM would be gained from including the effect of local molecular environments in a fragment or functional group, the performances of the original EEM without involving any chemical environments25,26and with only including the connectivity and hybridization states30for reproducing AIM charges were used for comparisons. Fig. 6 shows the comparison of AIM charges, obtained from three different EEM methods, with those calculated at the B3LYP/6-31+G(d,p) level for all the atoms in the training sets. Also included are the root mean square error (RMSE) and average absolution deviation (DEV) of correlation results for the calibrated results with respect to different types of EEM method.To avoid the all possible interference, atomic-charge parameters of the original and modified EEM method, with a total of 5 (as shown in Table S1) and 11 atom types (as shown in Table S2),respectively, are recalibrated and optimized using the same optimized method and training sets as that of the EEM method proposed in this work.

It is clear that the EEM-AIM charges obtained using the EEM method developed in this work are in good agreement with the DFT-AIM charges, better than those of modified EEM charges30and much better than those from original EEM method26for these training molecules. The square of correlation coefficient R2of EEM-AIM charges with DFT-AIM charges increases quite a lot from 0.9832 to 0.9974, and the data of root mean square error(RMSE) shows a steep drop, decreasing from 0.0872 to 0.0351 after by considering the effect of local chemical environments in a region in the EEM parameterization. This can also be reflected by the changes of the atomic charge distributions shown in Fig.6. A relatively wider spread of points of atomic charges in the plot, together with an outlier, can be found in Fig. 6a. When considering the factors of connectivity and hybridized states in the modified EEM, the range of the atomic charges points becomes lower and the outlier disappear (Fig. 6b). Particularly when including the effect of chemical environments in the main peptide fragments, five regions exhibiting a relatively high density of points can be observed. One region close to the x-axis with high negative charges, are mainly associated with nitrogen and oxygen atoms in the peptide groups, whereas the region with strong positive charges approximately more than 1.4e correspond to the C’ atoms in the peptides of C＝O group. This is in good agreement with the very reproducible AIM charges for the atoms in peptide bonds as shown in Fig. 4. This illustrates again that in order to yield quantitatively reliable atomic charges with the principle of electronegativity equalization, not only the factors of connectivity and hybridized states, but also the effect of chemical environments in a local region should be taken into account.

From the discussed above, making a distinction between the atoms in different fragments or functional groups, would further improve the fit in the training set, although it will require much more effort to minimize the fitness function due to the increase of the dimensionality in the calibration.

Fig. 6 Comparison of AIM charges, obtained from original (a) and modified EEM methods (b), and the EEM method presented in this study (c),with the results calculated at the B3LYP/6-31+G(d,p) level for all the atoms in the training sets, respectively.

Fig. 7 The frame structures of a set of test molecules: A = Ac-GASANHCH3 (C14H25N5O6) B = Ac-YGFM-NHCH3 (C28H37N5O6S).

3.4 Applicability of the EEM described in this work

In the section above, the EEM charges obtained from the current approach show better agreement with the DFT charges than those of original26and modified EEM charges30for the molecules contained in the calibration set. To further assess the applicability of the EEM method presented in this study, two terminally blocked tetrapeptides, Ac-Gly-Ala-Ser-Ala-NHMe(Ac-GASA-NHMe) and Ac-Tyr-Gly-Phe- Met-NHMe (Ac-YGFM-NHMe), that are not included the calibration set were used for test molecules. The framework structures of two test tetrapeptides as shown in Fig. 7 are directly taken from the peptide Atlas conference database (http://www.peptideatlas.org)published by NIST.

Plots A3 and B3 in Fig. 8 show the correlations between the AIM charges obtained from the EEM method proposed in this work and B3LYP/6-31+G(d,p) calculations for a set of two test molecules, respectively. For comparison, the AIM charges,calculated from original EEM and modified EEM methods, are also compared with the DFT-AIM charges at the same level as shown in plots A1 and B1, and A2 and B2, respectively. The corresponding calibrated results, i.e., the correlation coefficients R, the average and maximum absolute deviations, are listed in Table 2.

Table 2 Comparison of AIM charges, obtained from different types of EEM methods, with the results calculated at the B3LYP/6-31+G(d,p) level for the two test molecules (Ac-X-NHMe, X = GASA and YGFM) a.

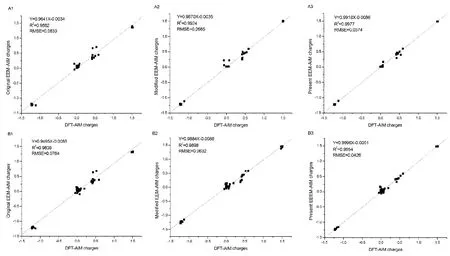
Fig. 8 Comparison of AIM charges，derived from original (A1 and B1) and modified EEM methods (A2 and B2), and the EEM method developed in this study (A3 and C3), with those calculated at B3LYP/6-31G+(d,p) level for the two test molecules, respectively.A1, A2, and A3 denote the predicted results for the test molecule of Ac-GASA-NHMe, while the B1, B2, and B3 is the predicted results for the test molecule of Ac-YGFM-NHMe.

It is apparent that the quality of fitness between present EEMAIM charges and DFT-AIM charges improves significantly compared to those of the original26and modified EEM-AIM charges30for two test molecules (as shown in Fig. 8). The square of linear correlation coefficients R2of two test tetrapeptides obtained by the EEM method presented in this work are greatly higher than those from the corresponding original and modified EEM methods. The value of root mean square error (RMSE)gradually decreases from 0.833 to 0.0374 (plots A1 to A3), and 0.0764 to 0.0426 (plots B1 to B3), respectively. In comparison with the original EEM method26, both of the average and maximum absolution deviations for the EEM charges decrease largely for the present EEM method (Table 2), although the calibration set used does not hold any of these two chosen polypeptides, taking Ac-YGFM-NHMe as an example, the average absolution deviations between the predicted EEM-AIM charges and DFT-AIM charges decreases from 0.0622 eV to 0.0231 eV, and the maximum value also drops to 0.0891 eV from 0.2399 eV when considering the local chemical environments in peptides fragments. It is should be noted that the parameters of the original and modified EEM methods are recalibrated under the same condition (i.e., the same training set, optimized method) as that of the present study.

The good performance of present EEM method for these two polypeptides further demonstrates that the local molecular environments in fragments or functional groups must be considered in the validity of EEM parameters, especially important for the lager systems which possess highly repeated fragments such as polypeptides, although some uncertainty may be brought for obtaining accurate EEM parameters through fitness function with the increase of variables. Atomic charges are very useful indicators. Fast calculation of accurate AIM charges using the EEM method developed in this work for polypeptides could be especially useful in the prediction of protein-protein, protein-DNA, and drug-receptor recognition and interactions.

4 Conclusions

A novel efficient approach, based on the Bader’s concept of high degree fragment transferability of atomic charges, has been presented to parameterization of atomic-charge parameters of EEM for polypeptides or proteins. Not only the factors of connectivity and hybridized states, but also the effect of local chemical environments in fragments or groups has been taken into account in the EEM parameterization. The AIM charges of large molecules can now be reconstructed rapidly using the transferable atomic-charge parameters of fragments through EEM method. The main peptide group (NH―HαCα―C＝O) of polypeptide in the backbone was used as the building blocks to model EEM parameters for reproducing atomic charges in polypeptides.

As comparison to the previous studies, a greater improvement of EEM model has been made after by introducing the Bader’s fragment atomic charge transfer model into the EEM calibration.This illustrates that in order to yield quantitatively reliable atomic charges with EEM method, not only the factors of connectivity and hybridized states, but also the effect of chemical environments in a local region should be taken into account. As a result, the most time-consuming derived AIM charges can be rapidly and accurately reproduced using the EEM parameters of submolecular fragments calibrated in this work,providing a new scheme for calibration and parameterization of EEM for larger systems which possess highly repeated segments such as polypeptides or polynucleotides.

Among all types of atomic charges, only the AIM charges show a significant meaning in experiments and can be obtained through the X-ray diffraction experiments15–17,37,38. Thus, rapid reproducing accurate AIM charge for large system seems to be more meaningfully, especially in the prediction of proteinprotein, protein-DNA, and drug-receptor recognition and interactions.

Supporting Information:Optimized Values of χ* and η* of C, H, O, N and S elements without including any chemical environments and with only considering the factors of connectivity and hybridized states for a set of 20 training molecules have been included. Quantum mechanically calculated atomic AIM charges for the atoms of the main peptide residues(NH―HαCα―C＝O) within dipeptides Ac-X-NH-CH3(X =any neutral residue) using B3LYP/6-31+G(d,p) method and for the number of 20 termally blocked amide acids Ac-X-NHMe(X = any neutral naturally occurring amino acid residue), as well as for the two test tetrapeptides of Ac-GASA-NHMe and Ac-YGPM-NHMe at the B3LYP/6-31+G(d,p) level have also been included. This information is available free of charge via the internet at http://www.whxb.pku.edu.cn.