电极介质覆盖SF6间隙纳秒脉冲电压放电特性研究

郑殿春 沈湘东 郑秋平 陈春天 赵大伟

摘 要：本文引入流體力学理论的对流-扩散机制，建立以自洽流体力学模型为基础的SF6气体电极介质覆盖下的纳秒脉冲电压下的放电数学模型。采用MacCormack二阶精度反耗散的稳定格式，既顾了计算精度、计算量和收敛速度的要求，又克服放电过程间隙参量奇异性对计算结果的影响。同时计算分析了0.4 MPa，纳秒脉冲电压上升沿20 ns条件下，幅值分别为10、14、19和25 kV，以及幅值15和25 kV条件下的20、30和40 ns下的SF6气体电极介质覆盖下的纳秒脉冲放电特性，以及放电过程带电粒子的运动行为与间隙电场影响机制， 获得了脉冲电压幅值和上升沿对其放电过程的位移电流、传导电流以及总电流之间制约关系。研究结果对拓宽SF6应用领域具有参考价值。

关键词：SF6;纳秒脉冲电压;电极介质覆盖;MacCormack格式;位移电流;传导电流

DOI：10.15938/j.emc.2019.11.011

中图分类号：TM 351

文献标志码：A

文章编号：1007-449X（2019）11-0084-08

收稿日期： 2017-03-21

基金项目：国家自然科学基金（51077032）

作者简介：郑殿春（1956—），男，博士，教授，研究方向为电介质失效诊断、极端条件下气/液体放电现象;

沈湘东（1989—），男，硕士，助理工程师，研究方向为极端条件下气体放电现象与应用;

郑秋平（1989—），女，硕士，工程师，研究方向为工业通信及其标准化管理;

陈春天（1964—），男，博士，教授，研究方向为材料物理理论与研究;

赵大伟（1965—），男，硕士，副教授，研究方向为电介质失效诊断、极端条件下气/液体放电现象。

通信作者：赵大伟

SF6 discharge behaviors of electrodecovered with dielectric under nanosecond impulse voltages

ZHENG Dianchun1， SHEN Xiangdong2， ZHENG Qiuping3， CHEN Chuntian1， ZHAO Dawei1

（1.Key Laboratory of Engineering Dielectrics and Its Application， Ministry of Education，Harbin University of Science and Technology，Harbin 150080， China;2.State Grid Tonglu Power Supply Company， Tonglu County 311501，China;3.Instrumentation Technology & Economy Institute， Beijing 100055， China）

Abstract：

The convectiondiffusion mechanism of fluid mechanics theory was introduced to establish the mathematical model of discharge under nanosecond impulse voltage of SF6 gas electrodecovered by dielectric based on selfconsistent fluid mechanics model. The stable form of secondorder precision inverse dissipation of MacCormack was used. Calculation amount and convergence speed were taken into consideration， and the influence of gap parameter singularity on the calculation results was overcome. Through calculation and analysis of 0.4 MPa， nanosecond impulse voltage rise along under the condition of 20 nanoseconds， amplitude is 10， 14， 19 and 25 kV  respectively， as well as amplitude under the condition of 15 and 25 kV under 20， 30 and 40 ns of SF6 gas electrode. Nanosecond pulse discharge properties of media coverage， and the dynamics of electrically charged particles in the discharge process electric field impact mechanism were illustrated. Pulse voltage amplitude， rising along the discharge process of displacement current and conduction current and the constraint relationship between the total current were obtained. The research results have reference value to broaden the application field of SF6.

Keywords：SF6; nanosecond impulse voltage; electrodecovered with dielectric; MacCormack format; displacement current; conduction current

0 引 言

纳秒脉冲电压气体放电现象的研究源于脉冲功率技术的发展。SF6作为一种电负性极强的气体电介质，具有优良的电绝缘和灭弧特性，被广泛应用于高电压、超高压电气设备领域。在高电压等级下，由VFTO（特快速暂态过电压）引起的GIS（封闭式组合电器）绝缘故障率已超过其在雷电冲击下的故障率，因此SF6在纳秒脉冲条件下的绝缘特性引起学者的极大重视[1]。

国外对纳秒脉冲下SF6的放电特性研究起步较早，在1991年Morrow R采用一维流体模型模拟了SF6在均匀电场中电流密度以及电子密度的变化规律，但在其模型中未考虑光致电离效应[2]。张乔根等对VFTO作用下SF6气体间隙击穿特性进行一系列研究，认为其放电特性与放电过程中空间电荷行为的差异有关，但对电荷分布及其运动等微观变化规律有待进一步深入研究[3-5]。冉慧娟、邵涛等对纳秒脉冲电源重复频率对SF6放电特性的影响进行研究，得到了重频耐受时间、施加脉冲个数与重复频数的关系[6-7]。以上研究都是在电极-SF6-电极结构下对SF6放电特性进行的研究。目前对电极介质覆盖条件下，SF6气体间隙纳秒脉冲放电特性研究相对较少，有待进一步深入探索和研究。

本文采用一维自洽流体力学模型，引入流体力学理论的对流—扩散机制，建立了SF6气体电极介质覆盖的纳秒脉冲放电模型，研究分析了纳秒脉冲下SF6电极介质覆盖放电特性，以及放电过程带电粒子的运动行为与间隙电场影响机制。本文的研究不但可以加深极端条件下SF6放电现象的认识理解，而且也为拓宽其应用领域提供技术参考。

1 模型及分析方法

Wu和Kunhardt等人的研究证明了运用流体力学模型描述气体放电现象的有效性[8]。因此本文在流体模型的基础上，引入对流-扩散机制 [9]，建立电极介质覆盖SF6物理模型如图1所示。

ne（x，t）t+je（x，t）x=Se（x，t），（1）

ni（x，t）t+ji（x，t）x=Si（x，t），（2）

nn（x，t）t+jn（x，t）x=Sn（x，t）。（3）

其中：n表示粒子密度;j表示带电粒子流通量;S表示源项;下标中的e、i、n分别表示电子、正离子和负离子，本文考虑了电子的碰撞、附着、复合，正负离子的复合以及光电离效应，则源项可表示为

Se（x，t）=（αe（x，t）-ηe（x，t）+

ge（x，t））μe（x，t）Eg（x，t）ne（x，t）-

βei（x，t）ne（x，t）ni（x，t），（4）

Si（x，t）=（αe（x，t）+

ge（x，t））μe（x，t）Eg（x，t）ne（x，t）-

βei（x，t）ne（x，t）ni（x，t）-

βni（x，t）nn（x，t）ni（x，t），（5）

Sn（x，t）=ηe（x，t）μe（x，t）Eg（x，t）ne（x，t）-

βni（x，t）nn（x，t）ni（x，t）。（6）

其中：α、β、η、g分別为碰撞电离系数、复合系数、附着系数以及光致电离系数。各带电粒子流密度的通量分别表示为

je（x，t）=-μe（x，t）ne（x，t）E（x，t）-

De（x，t）ne（x，t）x，（7）

ji（x，t）=μi（x，t）ni（x，t）E（x，t）-

Di（x，t）ni（x，t）x，（8）

jn（x，t）=-μn（x，t）nn（x，t）E（x，t）-

Dn（x，t）nn（x，t）x。（9）

其中：μ、D分别表示粒子的迁移率和扩散率;E为间隙的电场强度。

方程式（1）、式（2）和式（3）耦合间隙电场Possion方程构成了电极介质覆盖SF6物理模型图1的数学模型方程组。解析此方程组可以获得放电过程的粒子动力学行为、间隙电场以及外部激励特性之间制约机制。为此，根据气体放电理论，做如下假设：①在初始时刻各带电粒子均均匀分布于气体间隙上，即ne0=ni0=nn0=n0;②介质覆盖层的电导率为0，即当各带电粒子在运动到介质覆盖层后都在电极介质覆盖层上积累，即n（x1，t）=∫t0j（x1，t′）dt′，n（x2，t）=∫t0j（x2，t′）dt′，x1，x2分别表示左侧、右侧介质覆盖层位置。由于间隙电场的自洽性，所以用电流平衡方程（10）代替泊松方程来求解间隙的电场：

ε（x）E（x，t）t+jc（x，t）=jT（t）。（10）

其中：jc表示传导电流密度;jc（x，t）=e（ji-je-jn）;jT表示总电流密度，

jT（t）=ε0U（t）+1εg∫x2x1jc（x，t）dx/2d1εr+dgεg。（11）

由气体放电理论可知，气体放电过程中电子和离子密度在同一时刻在放电空间的不同位置可能相差几个数量级，同一位置在不同时刻的数值也可能相差几个数量级，导致了相应的电流密度和电场量变化的奇异性，对求解方法提出更高的要求[10]。本文采用MacCormack差分格式对上述方程组进行离散求解，此格式不但具有二阶精度，而且是一种反耗散的稳定格式，能在保证稳定性的前提下，兼顾了计算精度、计算量和收敛速度的要求[11-12]。

2 脉冲电压参数对放电特性的影响

间隙充满理想状态的SF6气体，其电子和离子输运参数、碰撞电离参数及光致电离参数均取自于文献[13]，假设初始电子和离子的密度相等，ne=ni=nn=n0=1×107 cm-3，并均匀分布在气体间隙上[14]。两侧电极介质覆盖层厚度均为1 mm，相对介电常数为4.2，气隙间距为2 mm。

2.1 纳秒脉冲电压幅值对放电特性的影响

高压电气设备使用SF6的压强通常0.4～0.6 MPa之间，除断路器的灭弧室外的大部分场合是0.4 MPa压强。因此，选择上升沿为20 ns、脉宽为35.3 ns的纳秒脉冲电压，通过改变其幅值研究0.4 MPa下SF6电极覆盖放电特性。

纳秒脉冲电压作用下，SF6气体间隙中的总电流由位移电流和传导电流密度组成，位移电流可由公式jd=ε0εrdE/dt计算获得。外施电压幅值为10 kV时，间隙总电流密度、位移电流密度和传导电流密度随时间的变化规律如图2所示。

从图中可以看出间隙总电流密度和位移电流密度的波形相似，这是因为此时纳秒脉冲电压幅值较低，SF6的电离度很小，此时传导电流密度的最大值仅为1.6×10-5 A/cm2，很微弱。

当纳秒脉冲电压幅值上升至14 kV时，间隙总电流密度、传导电流密度和介质覆盖层电荷密度随时间的变化规律如图3所示。

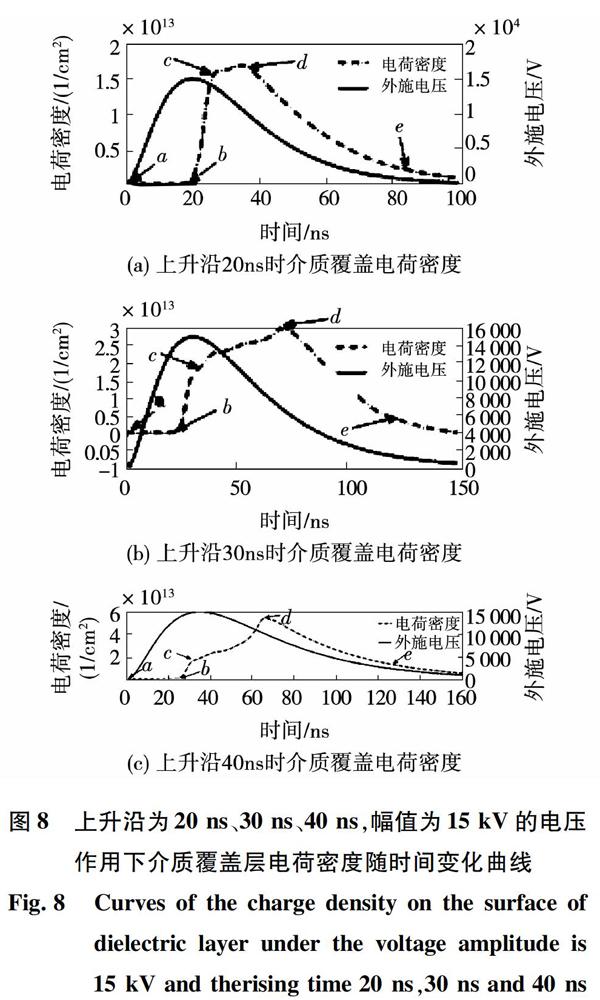
图3（b）中可以看到间隙传导电流密度在0～20 ns约为0，而在20～33 ns时间内迅速增加，这是因为在0～20 ns之间外电场强度较小，电子从外电场中获得的能量不足以通过碰撞电离产生大量的电子，但是电子将这部分能量通过碰撞传递给气体分子，使得气体分子处于激发态[15];在20 ns时气体中已经存在大量气体分子处于激发态，并且电子经电场加速也具有足够的能量，在20～33 ns之间和激发态的气体分子碰撞而发生雪崩效应，电子数量急剧上升，传导电流密度随之迅速上升。由于在脉冲上升沿积累的激发态分子在20～33 ns之间激发电离而密度迅速降低不能继续通过激发效应产生大量电子，另一方面由于介质覆盖层积聚电荷产生一个与外电场方向相反的反向电场，外电压也已经降低到10 kV左右，使得气体电离度下降，因此在33 ns后传导电流密度迅速降低。图3（c）表示左侧介质覆盖层电荷密度随时间变化规律。图中可以看出在29 ns，介质层上的电荷密度最大值1.45×1013 cm-3并在29～37 ns时间内基本保持在最大值附近，37 ns后隨着传导电流密度降低而迅速减小。

当纳秒脉冲电压幅值为19 kV时，间隙总电流密度、传导电流密度和左侧介质覆盖层电荷密度随时间的变化规律如图4所示。

看到间隙电压波形在30 ns以后和外施电压波形存在明显差异。而间隙总电流密度在约28 ns时出现一次小的幅值为0.65 A/cm2放电，在39 ns又出现了一次较大的幅值为1.85 A/cm2放电。图4（b）表示脉冲电压幅值为19kV时传导电流随时间变化规律，在23 ns后间隙总电流密度与传导电流密度值基本想等。在28 ns时传导电流有小幅下降，由于外施电压幅值持续增加而有效电离系数（α-=α-η）也迅速增大，气体的电离度增加，在39 ns时传导电流达到最大覆盖值1.85 A/cm2。图4（c）中可以清晰地看到覆盖介质层上电荷密度在18～22.5 ns出现第一次迅速增加，而22.5～36.5 ns之间的增长速度则明显变慢，在36.5～42 ns之间又出现第二次迅速增长的情况。

纳秒脉冲电压幅值为24 kV时，间隙总电流密度和间隙电压、传导电流密度、左侧介质覆盖层上电荷密度随时间的变化规律如图5所示。此时，间隙电压波形畸变、介质覆盖层上电荷密度剧增，并且在28ns时发生了强烈放电，其传导电流密度最大值达到10.5 A/cm2。

图6表示脉冲电压幅值为25 kV时气体间隙的电场强度变化规律，可以看到在0～24 ns之间气体间隙上电场随着外施电压变化而变化并且在气隙间均匀分布，而在20～40 ns之间电场分布极不均匀，主要集中在阳极侧介质覆盖层附近，其最大值可达4.2×105 V/cm。

2.2 纳秒脉冲电压上升沿对放电特性的影响

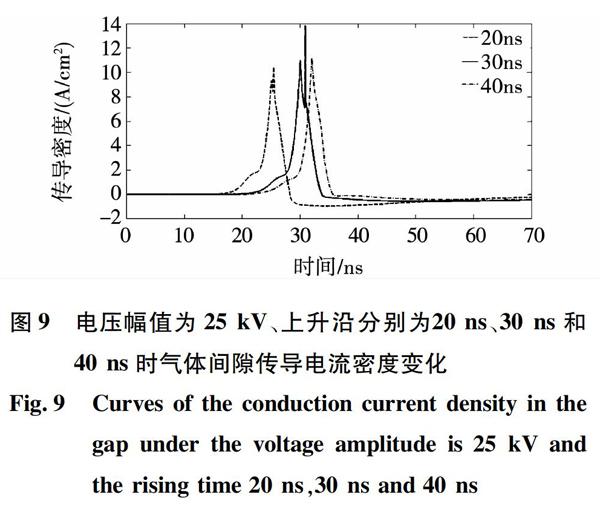
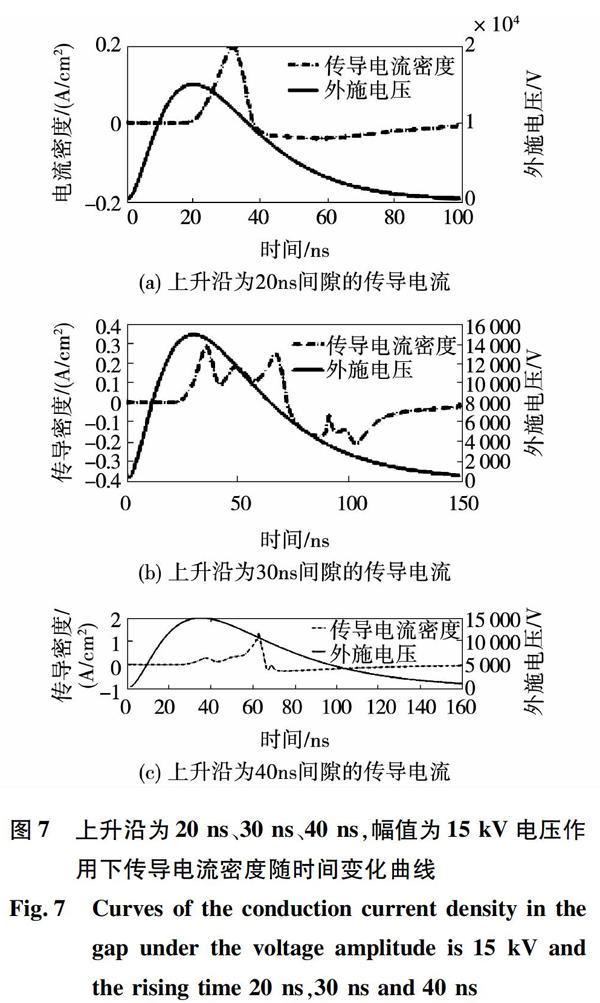
保持图1放电结构不变，施加纳秒脉冲电压幅值为15 kV和25 kV，其上升沿分别为20 ns、30 ns、40 ns，脉宽分别为35.3 ns、55.7 ns和67.2 ns的情况下，分析电极介质覆盖SF6放电特性。

图7表示在上升沿为20 ns、30 ns、40 ns，幅值为15 kV纳秒脉冲电压作用下传导电流密度随时间的变化。图7（a）表明，由于外施脉冲电压上升沿为20 ns，持续时间较短，电源注入放电间隙的能量也较少，导致气体电离程度较小，产生带电粒子也有限，因此传导电流密度较小，最大值为0.2 A/cm2。图7（b）中由于纳秒脉冲电压上升沿为30 ns，导致气体电离程度加强，可产生的带电粒子数量增多，因此传导电流密度增大为0.29 A/cm2。图7（c）所示脉冲电压上升沿为40 ns，由于外施脉冲电压持续时间长，向气体间隙注入了足够的能量，产生更多的带电粒子，故传导电流密度达到1.43 A/cm2。

4 結 论

本文采用一维自洽流体力学模型，引入流体对流-扩散机制，建立了SF6气体电极介质覆盖的纳秒脉冲放电模型，理论分析了纳秒脉冲下SF6电极介质覆盖放电特性，得到以下结论：

1）外施纳秒脉冲电压的上升沿保持20 ns不变，改变脉冲电压幅值，在5 ns左右都会出现一个脉冲电流，认为是由外施电压变化引起的位移电流。随着外施纳秒脉冲电压的幅值从10 kV上升到25 kV，传导电流密度最大值从1.6×10-5 A/cm2上升为10.5 A/cm2，并且传导电流最大值发生时间从60 ns提前到28 ns。纳秒脉冲电压幅值为19 kV时在28 ns和38 ns分别出现一个脉冲电流。随外施电压幅值从14 kV上升到25 kV，阳极侧介质覆盖层上积累的电荷密度最大值从1.46×1013 cm-3上升到1.18×1014 cm-3。

2）在外施电压幅值为15 kV，上升沿分别为20 ns、30 ns、40 ns时，传导电流密度最大值分别为0.19 A/cm2、0.30 A/cm2、1.43 A/cm2，同时介质层上积累的电荷密度从1.69×1013 cm-2增加到5.58×1013 cm-2。

3）在外施电压幅值为25 kV、上升沿分别为20 ns、30 ns、40 ns时，其传导电流密度最大值分别出现在28 ns、32 ns和35 ns，并且上升沿为30 ns时传导电流密度最大，约为1.32×1014 cm-2;不同上升沿，电场强度最大值都出现在左侧介质覆盖层附近，并且最大值发生的时间和传导电流密度最大值的时间几乎同步。

参 考 文 献：

[1] ZHENG D， ZHANG Z， ZHU S， et al. Numerical analysis of very fast transient overvoltage in GIS[C]//Electric Power EquipmentSwitching Technology （ICEPEST）， 2011 1st International Conference on. IEEE， 2011： 35-38.

[2] MORROW R. Theory of positive corona in SF6 due to a voltage impulse[J]. IEEE Transactions on Plasma Science， 1991， 19（2）： 86-94.

[3] 张连星，大气压下短气隙放电过程分析[D]，哈尔滨理工大学，2011.5.

[4] 杨仁旭 纳秒脉冲电极覆盖短气隙放电现象研究[D].哈尔滨理工大学，2014.04.

[5] 张璐， 张乔根， 刘石， 等. 特快速瞬态过电压和雷电冲击作用下特高压GIS绝缘特性[J].高电压技术， 2012， 38（2）： 335-341.

ZHANG Lu， ZHANG Qiaogen， LIU Shi，et al. Insulation characteristics of UHV GIS under VFTO and lightning impulse[J]. High Voltage Engineer，2012， 38（2）：335-341.

[6] 冉慧娟， 王珏， 王涛， 等. 纳秒脉冲下 SF6 气体放电特性[J]. 高电压技术， 2011， 37（6）：1690-1696.

RAN Huijuan， WANG Yu， Wang Tao， et al. Comparison of the characteristic in nanosecondpulsed dielectric barrierdischarge using different dielectric materials[J]. High Voltage Engineer， 2011， 37（6）：1690-1696.

[7] 邵涛，袁伟群，孙广生，等. 常压下重频纳秒脉冲气体放电试验研究[J]. 中国电机工程学报，2005， 25（8）： 161-166.

SHAO Tao， YUAN Weiqun， SUN Guangsheng， et al. Experimental study of repetitively nanosecondpulse breakdown in atmospheric air[J]. Proceedings of the CSEE， 2005， 25（8）： 161-166.

[8] WU C， KUNHARDT E E. Formation and propagation of streamers in N 2 and N 2-SF 6 mixtures[J]. Physical Review A， 1988， 37（11）： 4396.

[9] ZHENG D， ZHU S， ZHANG Z， et al. Dynamic behaviors of the streamer development and propagation in SF 6[C]//Electric Power EquipmentSwitching Technology （ICEPEST）， 2011 1st International Conference on. IEEE， 2011： 509-512.

[10] 郑殿春， 夏云双， 朱士华， 等. 均匀电场 SF_6 短气隙放电过程动态模拟[J]. 计算物理， 2012， 29（6）： 867-875.

ZHENG Dianchun， XIA Yunshuang， ZHU Shihua， et al. Dynamics simulation of SF6 discharge in a short gap under uniform electric field[J].Chinese Journal of Computational Physics，2012，29（6）：867-875.

[11] 吴江航， 韩庆书. 计算流体力学的理论， 方法及应用[M]. 科學出版社， 1988.

[12] ANDERSON JR J D. Fundamentals of aerodynamics[M]. Tata McGrawHill Education， 2010.

[13] Morrow R. A survey of the electron and ion transport properties of SF6[J]. IEEE Transactions on Plasma Science， 1986， 3（14）： 234-239.

[14] 王艳辉. 均匀大气压介质阻挡放电特性及模式研究 [D]. 大连： 大连理工大学学位论文， 2006.

[15] 王倩，空气及SF6放电过程的光学特性[D]， 哈尔滨：哈尔滨理工大学，2014.05.

（编辑：刘素菊）