低温余热磁悬浮发电机转子轴系振动机理研究

纪历

摘 要：采用磁悬浮高速直驱发电设备能够显著地提高低温余热发电系统的效率。以磁悬浮高速永磁发电机为对象，研究磁悬浮转子受到的电磁不平衡拉力及其轴系的径向振动情况。文中综合考虑磁悬浮转子静、动态偏心，结合麦克斯韦应力法与等效磁路法推导了电机不平衡拉力的解析模型，并结合转子质量不平衡激励以及磁悬浮轴承的控制反力研究了转子的振动情况。文中通过计算、仿真及试验对影响不平衡拉力的主要因素进行了详细分析，得到了其与偏心量幅度、发电机转矩角以及转子磁动势与偏心角度的初始相差等多个因素的关系，所得研究结论为抑制磁悬浮发电机转子振动提供了理论依据。

关键词：余热发电;磁悬浮转子;不平衡拉力;轉子偏心;永磁电机

DOI：10.15938/j.emc.2019.11.009

中图分类号：TM 355

文献标志码：A

文章编号：1007-449X（2019）11-0067-09

收稿日期： 2017-11-29

基金项目：江苏省自然科学基金（BK20190491）;中央高校基本科研业务费项目（2018B57414）

作者简介：纪 历（1984—），男，博士，研究方向为电力电子与电力传动。

通信作者：纪 历

Vibration mechanism analysis of magnetic levitation rotor system for low temperature waste heat power generation

JI Li

（College of Energy and Electrical Engineering，HOHAI University， Nanjing 210098， China）

Abstract：

By using high speed maglev generator， the efficiency of low temperature waste heat generation system were improved significantly. The unbalanced magnetic pull （UMP） in the maglev generator caused by dynamic and static eccentricity was calculated theoretically， and the analytical expression of the UMP was obtained based on Maxwell stress tensor method. Then， the vibration of a maglev rotor system under the action of the UMP and the mass unbalance force was analyzed by the numerical method. Lastly， the effects of different eccentricities， torque angles and loads on the rotor vibration were discussed in detail.The conclusions for the maglev rigid rotor system are useful for the future research.

Keywords：low temperature waste heat power generation; magnetic levitation rotor; unbalanced magnetic pull; rotor eccentricity; permanent magnet synchronous machines

0 引 言

现有低温余热发电设备通常采用“透平机—减速箱—发电机”的形式，由传动、支撑系统造成的损耗高达整机功率的10%，以至设备普遍存在发电效率低、成本高、体积大等不足，经济性不高，未能形成规模。借鉴磁悬浮航空发动机相关技术，开发磁悬浮高速透平发电机设备，无需机械轴承、变速箱及其附属的润滑和供油系统，相对于现有设备能够提高效率10%～15%。这对于发展我国高端制造业以及提倡低碳环保的国家政策都具有重要意义[1-4]。

然而磁悬浮轴承刚度远低于一般机械轴承[5]，在转子高速旋转时存在较大的动态偏心量从而引发电机不平衡拉力，而该不平衡拉力与转子质量不平衡力以及磁悬浮轴承的控制力共同作用将导致发电机转子发生复杂的振动情况，如果不加以处理可能导致整个磁悬浮系统失稳崩溃。因此，有必要研究磁悬浮发电机转子的振动机理。

现有研究对于偏心情况下转子振动特性的分析偏重于常规电机。如文献[6]研究了静、动态偏心对电机磁感应强度、输出转矩、损耗方面的影响，得到了许多有价值的结论。文献[7]根据有限元分析的结果应用RBF神经网络方法建立了径向不平衡力模型。文献[8]考虑了静止偏心与振动偏心同时存在的情况，建立了永磁转子的动力学模型。文献[9]基于有限元软件计算了大型永磁电机转子的不平衡响应并对电机的振动特性进行了分析。文献[10]应用正则摄动理论建立了永磁转子偏心气隙磁场的解析模型，并计算了空载情况下的不平衡拉力。但是对于磁悬浮电机，这方面的研究较少，文献[11]研究了磁悬浮刚性转子系统的振动机理，并建立了其动力学模型，但是文中没有考虑到电机不平衡拉力的影响。文献[12]通过有限元软件研究了不平衡拉力对转子振动以及磁悬浮轴承刚度的影响，得到了许多有价值的结论，但是文中结论是基于特定机型的有限元的分析，没有得到力矩的解析模型。文献[13-14]考虑磁路饱和建立了无轴承开关磁阻电机径向电磁力模型，但没有考虑不同偏心情况对不平衡拉力以及转子振动的影响。文献[15]根据虚位移法建立了无轴承永磁电机的径向力模型，但是推导过程中忽略了转子动态偏心的影响。

综上所示，现有文献对于磁悬浮电机转子轴系振动特性的研究并不完善。本文以磁悬浮高速永磁发电机为对象，综合考虑磁悬浮转子静、动态偏心情况，结合麦克斯韦应力法与等效磁路法推导了电机不平衡拉力的解析模型，并结合转子质量不平衡激励以及磁悬浮轴承的控制反力研究转子的力矩耦合与振动情况，所得研究结论可以为抑制磁悬浮发电机转子振动提供理论依据。

1 永磁电机不平衡拉力的数学模型

由于加工和装配的误差导致磁悬浮轴承定子的中心、磁悬浮位移传感器的测量中心、磁悬浮保护轴承[16]中心以及电机定子中心不在一条直线上，而根据磁悬浮轴承的工作原理，静态时转子将悬浮于保护轴承的中心，这导致电机定、转子之间存在初始的静态偏心。同时由于磁悬浮轴承的支承刚度相对较小，当转子高速转动时会绕其几何对称轴与惯性主轴之间的一条轴线旋转，产生动态偏心。此时，转子质心截面的示意如图1所示。

图中O为电机定子的中心，O1为磁悬浮保护轴承的中心，O′1为转子的几何中心;δ0是名义气隙长度;d0和γ0为只考虑静态偏心时的初始偏心量和偏心角度;d和γ为考虑动态偏心后的实际转子偏心量和偏心角度;x和y为转子几何中心相对于磁悬浮中心水平和竖直方向的偏移量。（文中假定x方向与定子A轴方向相同）

由于转子半径远大于转子中心偏移量，则任意角度θ处的气隙长度可近似表达为：

δ（θ）≈δ0-dcos（θ-γ）。（1）

式中的偏心量和偏心角度均可表示为x和y的函数形式。

d=（d0cosγ0+x）2+（d0sinγ0+y）2，（2）

tanγ=d0sinγ0+yd0cosγ0+x。（3）

根据文献[17]，电机任意气隙处的磁导率可以被处理为一个傅里叶级数的形式：

Λ（θ）=μ0dSδ（θ）=μ0dSδ0[1-εcos（θ-γ）]=

dS∑∞n=0Λncosn（θ-γ）。（4）

式中：dS为单位角度θ所对应的磁极面积;ε是相对偏心量，ε=d/δ0。系数Λn如式（5）所示：

Λn=μ0δ01-ε2，n=0，

2μ0δ01-ε21-1-ε2εn。n>0。（5）

根據永磁电机的运行原理，在负载情况下，电机内部的磁动势包括永磁体等效磁动势Fj与电枢磁动势Fs两部分，两个磁动势在稳态时保持同步，且在不同的控制策略下呈现不同的相位差。则气隙中的合成磁动势可以表示为：

F（θ）=Fj（θ）+Fs（θ）=

Fj0cos（α-pθ）+Fs0cos（α-pθ-λ）。（6）

式中：p为磁极对数;Fj0与Fs0分别表示定、转子磁动势的基波幅值;α为任意时刻转子d轴与定子A轴的相对电角度，其频率等于发出电能的频率ωe=pωr;λ为定、转子磁动势的夹角（转矩角），其与电机的控制策略有关。

忽略铁磁材料的磁势，根据等效磁路法，得到任意角度θ处气隙的磁感应强度的表达式为

B（θ）=Λ（θ）F（θ）S=

F（θ）∑∞n=0Λncosn（θ-γ）。（7）

根据麦克斯韦应力法的基本公式，忽略气隙磁导级数中的高次项，在计算中只保留前4项，则在一对极的情况下，转子在x和y方向上受到的电磁不平衡拉力如式（8）所示，式中μ0为真空磁导率，kn为不平衡拉力系数，见式（9）。

fump_x=LRπ8μ0[k1cosγ+k2cos（γ+λ）+

k3cos（γ-λ）+k4cos（2α-γ）+

k5cos（3γ-2α）+k6cos（2α-γ-λ）+

k7cos（2α-γ-2λ）+

k8cos（3γ-2α+2λ）+

k9cos（3γ-2α+λ）]，

fump_y=LRπ8λ0[k1sinγ+k2sin（γ+λ）+

k3sin（γ-λ）+k4sin（2α-γ）+

k5sin（3γ-2α）+k6sin（2α-γ-λ）+

k7sin（2α-γ-2λ）+

k8sin（3γ-2α+2λ）+

k9sin（3γ-2α+λ）]。（8）

k1=4F2j0Λ0Λ1+2F2j0Λ1Λ2+2F2j0Λ2Λ3+4F2s0Λ0Λ1+2F2s0Λ1Λ2+2F2s0Λ2Λ3，

k2=4Fj0Fs0Λ0Λ1+2Fj0Fs0Λ1Λ2+2Fj0Fs0Λ2Λ3，

k3=4Fj0Fs0Λ0Λ1+2Fj0Fs0Λ1Λ2+2Fj0Fs0Λ2Λ3，

k4=2F2j0Λ0Λ1+F2j0Λ1Λ2+F2j0Λ2Λ3，

k5=2F2j0Λ0Λ3+F2j0Λ1Λ2，

k6=4Fj0Fs0Λ0Λ1+2Fj0Fs0Λ1Λ2+2Fj0Fs0Λ2Λ3，

k7=2F2s0Λ0Λ1+F2s0Λ1Λ2+F2s0Λ2Λ3，

k8=2F2s0Λ0Λ3+F2s0Λ1Λ2，

k9=4Fj0Fs0Λ0Λ3+2Fj0Fs0Λ1Λ2。（9）

从上式可以看出，负载情况下转子受到的不平衡拉力非常复杂。常规电机中静态偏心量占主导地位，因此若忽略动态偏心量（即d和γ为定值），此时不平衡拉力包含3个方向固定的力矢量;3个两倍频正序分量以及3个两倍频负序分量。然而磁悬浮转子运行时存在较大动态偏心，转子的偏心角度并不固定，而是与转速同频的旋转，因此设α=ωrt;γ=ωrt+φ，这里假定初始时刻转子d轴与定子A轴重合，而φ表示定子A轴与偏心位置的初始相位差。将其带入式（8）不难看出稳态时磁悬浮转子受到的不平衡力中所有9项均为与转速同频的正序分量，因此总的不平衡拉力呈现出与转速同频且同向的旋转力矢量，但其幅值与相位并不确定，取决于偏心量、转矩角（取决于负载情况以及电机控制策略）、磁动势与偏心角度的初始相差等多个因素。

由于式（8）过于复杂难以求解，有必要对其进行简化，为保证结论具有普遍性，对式中的各个分量进行定性的分析。在不同的偏心率与负载率的情况下分析各个分力的大小，得到的曲线如图2所示。

不难看出在整个负载范围以及10%偏心率以内系数k5、k8、k9的幅值极其微小，因此在分析振动情况时式（8）中的第5、8、9项可以忽略不计。而式（8）中第2、3两项系数相同，且相位关于γ对称，可以与第1项一起合成为一个与偏心方向同向的力矢量;第4、6、7三项均与未知角度φ相关，因此可以将其合成看作一个与偏心方向不同向的同频分量，且该分量的相位随负载以及偏心情况的改变而改变。

2 考虑不平衡拉力的磁悬浮转子动力学建模

图3给出磁悬浮发电机转子轴系的结构简图。其由磁悬浮转子、发电机定子、磁悬浮轴承、位移传感器以及保护轴承等部分组成。图中，A、B为径向磁悬浮轴承的支承位置，xA、xB分别为对应x方向径向磁悬浮轴承处的位移，OC为转子形心。空间坐标系及其正方向如图中箭头所示。

1—透平机叶轮;2—径向磁悬浮轴承A;3—发电机定子;4—磁悬浮转子;5—径向磁悬浮轴承B;6—径向位移传感器;7—保护轴承。

可以看出，正常工作时，磁悬浮转子在径向上受到质量不平衡力、电机不平衡拉力以及磁悬浮轴承控制力的共同作用。首先，磁悬浮轴承的控制力fmb在工作点附近可以看做是关于位移和控制电流的线性函数[4]：

fmb=kdd+kii。（10）

式中d为转子在某方向的偏心位移;i为磁悬浮轴承的控制电流;kd表示该磁悬浮轴承的位移刚度;ki为电流刚度。控制电流i则由磁悬浮控制系统根据偏心位置大小以及特定的控制策略计算，考虑磁悬浮控制一般采用PID控制策略，i的表达式如下：

i=（-d）GPIDGA。（11）

式中GA為磁悬浮系统功率放大器的传递函数，若功放的带宽足够大可以看做是一个比例环节。

电机不平衡拉力fump如式（8）所示。而质量不平衡力fubm在x轴、y轴上分量可以表示为

fubm_x=m（ep-Δd）ω2rcos（ωrt+φ），

fubm_y=m（ep-Δd）ω2rsin（ωrt+φ）。（12）

式中，ep为转子偏心距（质心到形心的距离），Δd=x2+y2为形心到旋转中心的距离，即动态偏心量，φ为质量不平衡力的相位。

根据式7～式10以及转子动力学的基本原理，可以建立径向磁悬浮刚性转子系统的动力学模型：

Mx··+Gx·=Kdx+Kii-Efub。（13）

式中，x=[xA，xB，yA，yB]T为磁悬浮转子在A、B轴承处相对于平衡位置的位移量;i为磁悬浮轴承的控制电流矩阵;fub表示不平衡激励，主要包括质量不平衡力fubm与电磁不平衡拉力fump;M为广义质量矩阵;G为陀螺矩阵;Kd为磁悬浮位移刚度矩阵;Ki为磁悬浮电流刚度矩阵;E为不平衡激励响应系数矩阵。

3 结果分析

3.1 电机不平衡拉力的计算结果分析

文中以一台100 kW的磁悬浮高速永磁发电机为对象对磁悬浮转子受到不平衡拉力及其振动情况进行研究，该发电机的主要设计参数见表1。

首先，根据计算的结果分析空载时磁悬浮电机不平衡电磁拉力的情况，如图4所示。图4（a）、图4（b）为忽略静态偏心，动态偏心幅值为0.1 mm时转子的受力情况，其中4条曲线分别表示了在4种不同的初始动偏心角度下转子x在方向受到的不平衡拉力，曲线1～4对应初始动偏心角φ=0°、30°、60°、90°的情况，此时不平衡拉力的幅值分别为：60.0 N、54.7 N、35.2 N、20.3 N。可以看出空载情况下，转子受到的不平衡拉力不仅取决于偏心量，同时与偏心位移与转子磁动势位置的夹角有一定的关系，在相同的动偏心量情况下，若转子磁动势位置与偏心位置相同（φ=0°），则转子受到的不平衡拉力最大，且该拉力的相位与转子的动不平衡相位相同。若转子磁动势的相位与偏心相位不同则不平衡拉力的幅值减小，且相位发生偏移，当转子磁动势方向与偏心方向垂直时（φ=90°），不平衡拉力的幅值最小。将x、y方向的不平衡拉力合成为矢量形式，如图4（b），可以看出，在只有动态偏心的情况下不平衡拉力矢量轨迹为圆形，x、y方向受到的不平衡拉力幅值始终相同，转子磁场方向与偏心方向的相差只影响不平衡力的幅值和相位，而不会使合力的轨迹发生畸变。

图4（c）、图4（d）为同时考虑静态偏心（幅值0.02 mm）与动态偏心（幅值0.1 mm）时转子受不平衡拉力的情况，图中曲线1～3分别对应静偏心角度γ0=0°、45°、90°时的情况，为验证静偏心的影响，此时设置初始动偏心角φ=0°。可以看出随γ0改变，拉力的幅值变化并不大，但是其波形出现了直流分量，如图4（c）对应x方向的受力情况，曲线1～3的均值分别为6.25 N、4.5 N、3×10-15 N，可见静偏心量位于全部位于x方向时，Fx偏移量最大，而当静态偏心完全位于y方向时，x方向不受影响，正负半周对称。而y方向的情况则与之相反。可以得出结论，静态偏心将会使转子受到的不平衡拉力产生偏移，偏移的方向与静偏心的方向相同。

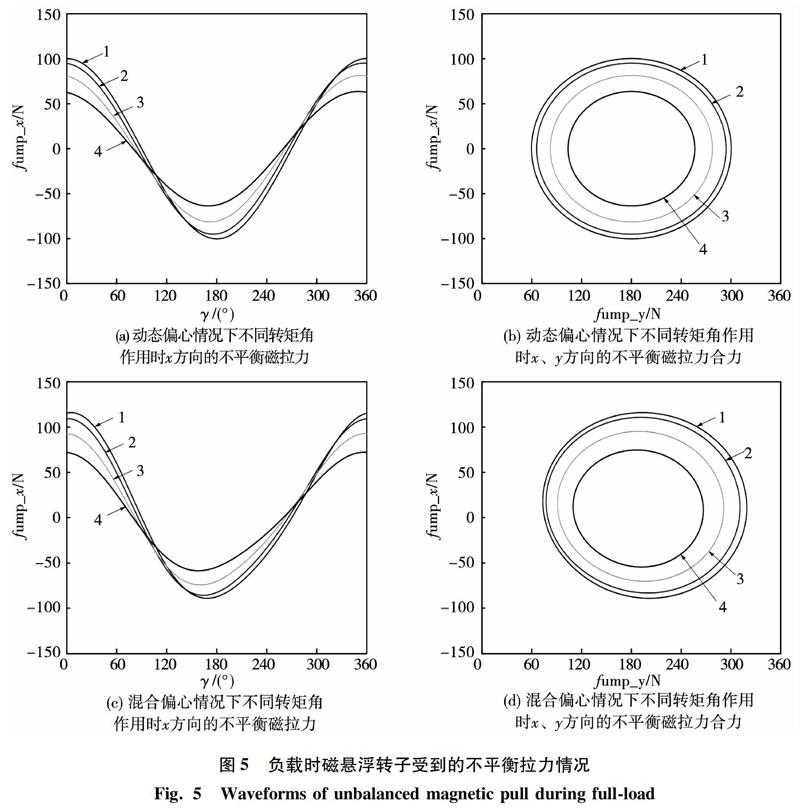
负载时磁悬浮转子的受力情況如图5所示。图5（a）、图5（b）为只考虑动态偏心（0.1 mm），且初始相差角φ=0°时转子受到不平衡拉力的情况。考虑到不同的电机控制策略的影响，最终反映在定、转子转矩角不同。文中计算了4种情况，对应图5（a）中曲线1～4表示定转子转矩角λ为0°、30°、60°、90°时转子x方向受到的不平衡拉力，其幅值分别为100.3 N、95.1 N、81.4 N、63.6 N。可以看出虽然4中情况下定转子磁动势的幅值相同，但是转矩角的差异同时影响了不平衡拉力的幅值和相位。当转矩角为零时，转子受到的不平衡拉力幅值最大，而随着转矩角的增大，转子受到的不平衡力逐渐减小，且相位也随之发生变化，当转矩角为90°时，转子受到的不平衡拉力最小。

图5（c）、图5（d）为同时考虑静态偏心（幅值0.02 mm，静偏心角度γ0=45°）与动态偏心（幅值0.1 mm）时不平衡拉力的情况。图中曲线1～4的定义与图5（a）、图5（b）中相同。可以看出，首先，与空载时相同，转子受到的不平衡拉力沿x、y轴的正方向发生了偏移，且其幅值的变化情况与图5（a）、图5（b）相同，转矩角为零时拉力最大，为90°时拉力最小。

通过空载与负载两种情况下对不平衡拉力的分析可以得到以下的结论：①初始相差φ对不平衡拉力有较大影响，当φ=0°时，转子受到的不平衡拉力最大，而φ=90°时，不平衡拉力的幅值最小;②较小的静态偏心对不平衡拉力幅值的影响不大，但会使得其出现直流分量，且该直流分量的大小与静态偏心量幅值成正比，方向与静态偏心方向相同;③转矩角λ对不平衡拉力具有较大影响，在其他条件相同的情况下，λ=0°时，转子受到的不平衡拉力幅值最大，λ=90°时，转子受到的不平衡拉力最小。

3.2 磁悬浮转子振动情况分析

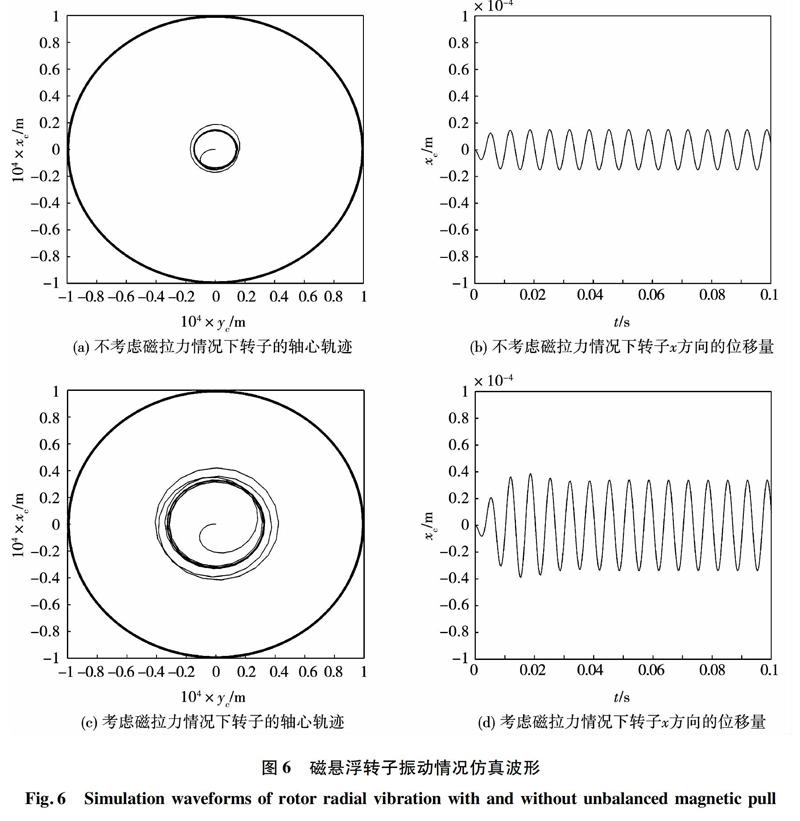
文中第2节推导出考虑不平衡激励的磁悬浮转子动力学建模如式（11）所示，其满足阻尼系统在简谐力作用下的受迫振动形式。以表1中的所述磁悬浮发电机为对象，设定转速9 000 r/min、转子偏心距ep=10 μm，求解式（11），模拟转子实际的振动情况，得到的仿真结果如图6所示。

图6（a）、图6（b）为只考虑质量不平衡力时转子的轴心轨迹以及转子在x方向的振动波形。图6（a）中外圈表示转子极限的振动范围（0.1 mm），超过这一数值则转子将会与保护轴承产生碰撞。从图中可以看出，在当前转速下，若只有质量不平衡力作用，则转子振动幅值较小，稳定后只有15 μm。图6（c）、图6（d）为质量不平衡力与电磁不平衡拉力共同作用时转子的轴心轨迹以及转子在x方向的振动波形。可以看出计及不平衡拉力后，转子振动的幅值明显增加，稳定后达到了34 μm，比只考虑质量不平衡力时增大了一倍有余。可见，电磁不平衡拉力对磁悬浮转子振动的影响不容忽视。

4 試验验证

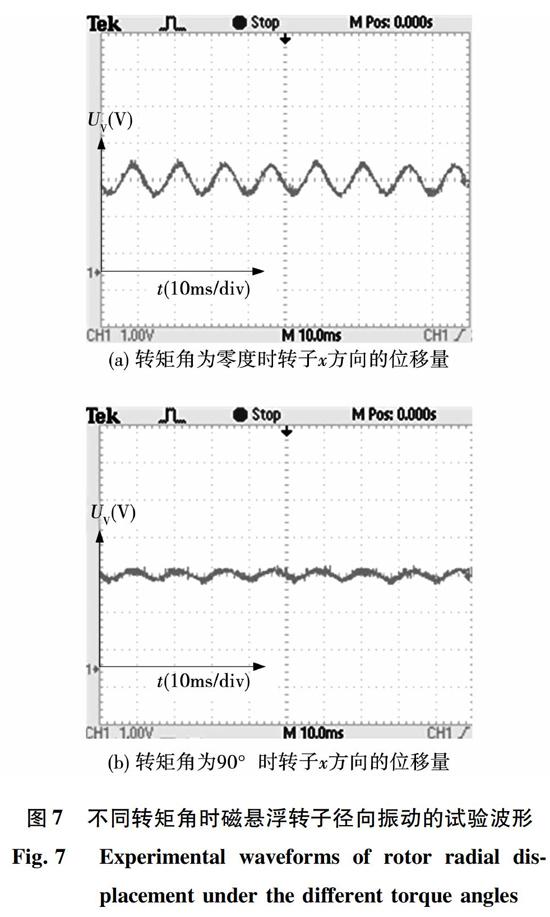
为验证结论的正确性，文中以一台100 kW的磁悬浮永磁发电机为对象进行了试验研究，其主要参数如表1所示。由于不平衡拉力难以测试，试验主要考察电机在不同转矩角时不平衡力对转子悬浮性能的影响。试验中使用变频器将电机拖动到4 800 r/min的转速，此时通过矢量控制算法调整电机的转矩角λ并观测转子的振动情况，如图7所示。

图7为磁悬浮转子径向振动的波形，图7（a）中电机的转矩角接近零度，电枢电流大量作用于转子d轴，此时径向位移传感器检测到的振动信号频率为80 Hz、峰峰值为1.04 V，对应传感器的测量精度20 V/mm，可知在当前转速下，转子在受到质量不平衡力和不平衡拉力的共同作用下产生了与转速同频的受迫振动，振动的幅值为26 μm。在相同的转速和同样的磁悬浮控制参数下，调整变频器矢量控制算法，将转矩角调整为90°，转子振动的波形如图7（b）所示，此时转子振动的幅值减小为12 μm，仅为图7（a）中的46.15%。考虑到两次试验的转速和磁悬浮轴承的控制参数相同，即图7（a）、图7（b）中转子受到的质量不平衡力和磁悬浮轴承的支撑特性完全相同，而转子的振动情况却发生了很大变化，证明磁悬浮转子确实受到了电磁不平衡拉力的影响，且情况与第3节中理论分析结果一致，转矩角越小，不平衡拉力的影响越大。

5 结 论

本文以磁悬浮高速永磁发电机为对象，研究了磁悬浮转子受到的电磁不平衡拉力及其轴系的径向振动情况。文中根据等效磁路法和麦克斯韦张力法推导了该不平衡拉力的解析表达式，并通过计算、仿真及试验对影响不平衡拉力的主要因素进行了详细分析。通过研究本文可以得到以下结论：

（1）在动态偏心占主导的磁悬浮电机中，永磁转子受到的不平衡电磁拉力表现为一个与转速同频且同向的旋转力矢量，其幅值与相位取决于偏心量、定转子转矩角λ以及转子磁动势与偏心角度的初始相差φ等多个因素;

（2）空载情况下，初始相差φ对不平衡拉力有较大影响。在偏心量幅值相同的前提下，若φ=0°，则转子受到的不平衡拉力最大，且该拉力的相位与转子的动不平衡位移位相同。当φ=90°，不平衡拉力的幅值最小;

（3）负载情况下，不平衡拉力受到转矩角λ的影响。在定、转子磁动势幅值相等的条件下，若λ=0°，则转子受到的不平衡拉力幅值最大。而随着λ角度增大，转子受到的不平衡拉力逐渐减小，且相位也随之发生变化，当λ=90°时，转子受到的不平衡拉力幅值最小;

（4）仿真和试验证明，电磁不平衡拉力对磁悬浮转子振动有较大影响，不容忽视，而通过调整电机控制策略能够有效的减小该不平衡拉力。

参 考 文 献：

[1] RANA S， ORRB， IQBAL A， et al. Modelling and optimization of lowtemperature waste heat thermoelectric generator system [J]. Energy Procedia， 2017，110： 196-201.

[2] CHIAROTTIU， MOROLI V， MENCHETTI F， et al. Development of a small thermoelectric generators prototype for energy harvesting from low temperature waste heat at industrial plant [J]. Journal of Nanoscience & Nanotechnology， 2017， 17（3）： 1586-1591.

[3] 王正， 崔超. 基于有机朗肯循环的低温余热发电系统设计与分析[J]. 电力与能源， 2013， 34（4）： 321-324.

WANG Zheng， CUI Chao. Design and analysis on lowtemperature waste heat power generation using organic rankine cycle [J]. Power & Energy， 2013， 34（4）： 321-324.

[4] JI L， XUL， JIN C. Research on a low power consumption sixpole heteropolar hybrid magnetic bearing [J]. IEEE Transactions on Magnetics， 2013， 49（8）： 4918-4926.

[5] GAOH， XU L. Realtime feedforward force compensation for active magnetic bearings system based on H∞ controller [J]. Chinese Journal of Mechanical Engineering， 2011， 24（1）： 58-66.

[6] 孔汉， 刘景林. 永磁伺服电机转子偏心对电机性能的影响研究[J]. 电机与控制学报. 2016， 20（1）： 52-59.

KONG Han， LIU Jinglin. Study of rotor eccentricity effect on permanent magnet servo motor performance [J]. Electric Machines and Control 2016， 20（1）： 52-59.

[7] 修杰， 王世宇. 轉子偏心时双凸极永磁开关磁阻电机径向力静态特性分析及其RBF神经网络建模[C]//第25届中国控制与决策会议. 2013， 贵阳， 中国： 5174-5179.

XIU Jie， WANG Shiyu. DSPM radial force static characteristic analysis and RBF NN modeling under rotor eccentric [C]// The 25th Chinese Control and Decision Conference （CCDC）. 2013， Guiyang， China： 5174-5179.

[8] 岳二团， 甘春标， 杨世锡. 气隙偏心下永磁电机转子系统的振动特性分析[J]. 振动与冲击， 2014， 33（8）： 29-34.

YUE Ertuan， GAN Chunbiao， YANG Shixi. Vibration characteristics analysis of a rotor for a permanent magnet motor with airgap eccentricity [J].Journal of Vibration and Shock， 2014， 33（8）： 29-34.

[9] 姜新通， 李伟凯， 陈言， 等. 低速直驱式大功率永磁同步电动机振动特性研究[J]. 电机与控制学报. 2017，21（7）： 73-77.

JIANG Xintong， LI Weikai， CHEN Yan，et al. Vibration characteristics research for the low speed direct drive high power PMSM [J]. Electric Machines and Control， 2017，21（7）： 73-77.

[10] 李琛， 章跃进， 周晓燕，等. 定子开槽表贴式永磁电机转子偏心空载气隙磁场全局解析法[J]. 电机与控制学报. 2014， 18（10）： 27-35.

LI Chen， ZHANG Yuejin， ZHOU Xiaoyan， et al.Exact analytical solution of opencircuit airgap magnetic field for slotted surfacemounted permanentmagnet motors with rotor eccentricity [J].Electric Machines and Control， 2014， 18（10）： 27-35.

[11] 房建成， 张会娟， 刘虎. 磁悬浮刚性转子系统振动机理分析与动力学建模[J]. 控制理论与应用. 2014， 31（12）： 1707-1713.

FANG Jiancheng， ZHANG Huijuan， LIU Hu. Vibration mechanism analysis and dynamic model development of magnetically suspended rigid rotor system [J]. Control Theory & Applications. 2014， 31（12）： 1707-1713.

[12] HAN B， ZHENG S， LIU X. Unbalanced magnetic pull effect on stiffness models of active magnetic bearing due to rotor eccentricity in brushless DC motor using finite element method [J]. Mathematical Problems in Engineering. 2013： 1-10.

[13] 楊艳， 邓智泉， 曹鑫， 等. 无轴承开关磁阻电机径向电磁力模型[J]. 电机与控制学报， 2009， 13（3）： 377-382.

YANG Yan， DENG Zhiquan， CAO Xin，et al. Magnetic radial force model of bearingless switched reluctance motor [J]. Electric Machines and Control 2009， 13（3）： 376-382.

[14] 曹鑫， 邓智泉， 杨钢， 等. 无轴承开关磁阻电机麦克斯韦应力法数学模型[J]. 中国电机工程学报. 2009， 29（3）： 78-83.

CAO Xin， DENG Zhiquan， YANG Gang，et al. Mathematical model of bearingless switched reluctance motors based on maxwell stress tensor method [J]. Proceedings of the CSEE. 2009， 29（3）： 78-83.

[15] 孙晓东， 陈龙， 杨泽斌， 等. 考虑偏心及绕组耦合的无轴承永磁同步电机建模[J]. 电工技术学报， 2013，28（3）： 63-70.

SUN Xiaodong， CHEN Long， YANG Zebin， et al. Modeling of a bearingless permanent magnet synchronous motor considering rotor eccentricity and coupling relationship of windings[J]. Transactions of China Electrotechnical Society， 2013，28（3）： 63-70.

[16] ZHU Y， JIN C， XU L. Dynamic response of rotor drops onto doubledecker catcher bearing [J]， Chinese Journal of Mechanical Engineering. 2013， 26 （1）： 104-113.

[17] GUOD， CHU F， CHEN D. The unbalanced magnetic pull and its effects on vibration in a threephase generator with eccentric rotor [J].Journal of Sound and Vibration， 2002， 254（2）： 297-312.

（编辑：刘素菊）