应用四层BP神经网络的棉纱成纱质量预测

查刘根， 谢春萍

(生态纺织教育部重点实验室(江南大学)， 江苏 无锡 214122)

纺纱工艺是纺织生产加工过程中一道十分关键的工序，纱线品质的高低不仅影响着后道加工工序的效率，也直接决定了最终织物产品的质量。另外，纺纱过程中涉及的参数种类众多，客户对纱线品质的要求不同，需要经常对工艺参数进行大量调整，而且从原棉到纱线，中间经过了很长的加工流程[1-2]。然而，目前对于国内大多数纺织企业来说，依据纱线品质指标确定配棉方案和调整加工工艺参数时所采用的手段依然是凭借着历史生产经验，而且还需通过进一步的大量试纺来调节和确定最后生产方案，浪费了大量时间和原材料，影响了企业整个生产加工进程。对于我国大多数纺织企业来说，迫切需要找到一种能够代替历史经验的高效智能化的纱线质量预测方法来优化其纺纱工艺，从而提高生产效率和竞争力，合理优化纺纱加工工序，科学地设定生产工艺参数和选择最经济的配棉方案，同时要达到客户及后道工序对纱线品质的要求。

因其突出的优点BP神经网络用途十分广泛。其结构简单，具有很强的自适应学习能力，很好的容错性，近十几年来被广泛应用于数据预测等问题上[3-5]。在进行质量预测问题的建模时，设计者构造的一般都是单隐层的三层神经网络，因为万能逼近定理证明三层网络模型就可完成任意m维和n维之间的映射。

理论上说，隐含层层数的增加会使网络结构更加复杂化，从而拉长网络误差反向传播的路径，同时还会降低训练的效率，但是，考虑到纱线质量预测模型是一个小样本预测模型，且输入和输出单元数较少，所以，本文在进行棉纱断裂强力和条干CV值的预测时，提出双隐层的四层BP神经网络结构，来进行2种模型的训练和仿真实验，并与单隐层的三层BP神经网络进行对比分析。

1 BP神经网络算法与设计

实际上，标准的BP神经网络模型结构十分简单，一共包含3个组成部分，最前面的是输入参数的输入层，中间是可具有1个或者多个隐含层的中间层，最后面是网络的输出层，提供最后运算结果。BP神经网络的训练过程可拆分为2步：第1步是外界输入信息由输入层到输出层的正向传播；第2步是网络处理后的误差信号沿着原来的路径反向传播。网络在传递误差的同时，会进行部分参数的修正，也就是各层之间的连接权值以及隐含层和输出层的阈值大小都会随着反传误差的传递不断地发生变化，当权值和阈值调整到某个适当值时，训练误差将会满足设计者的要求，此时网路训练终止[6]。图1示出一个最基本的BP神经网络模型。

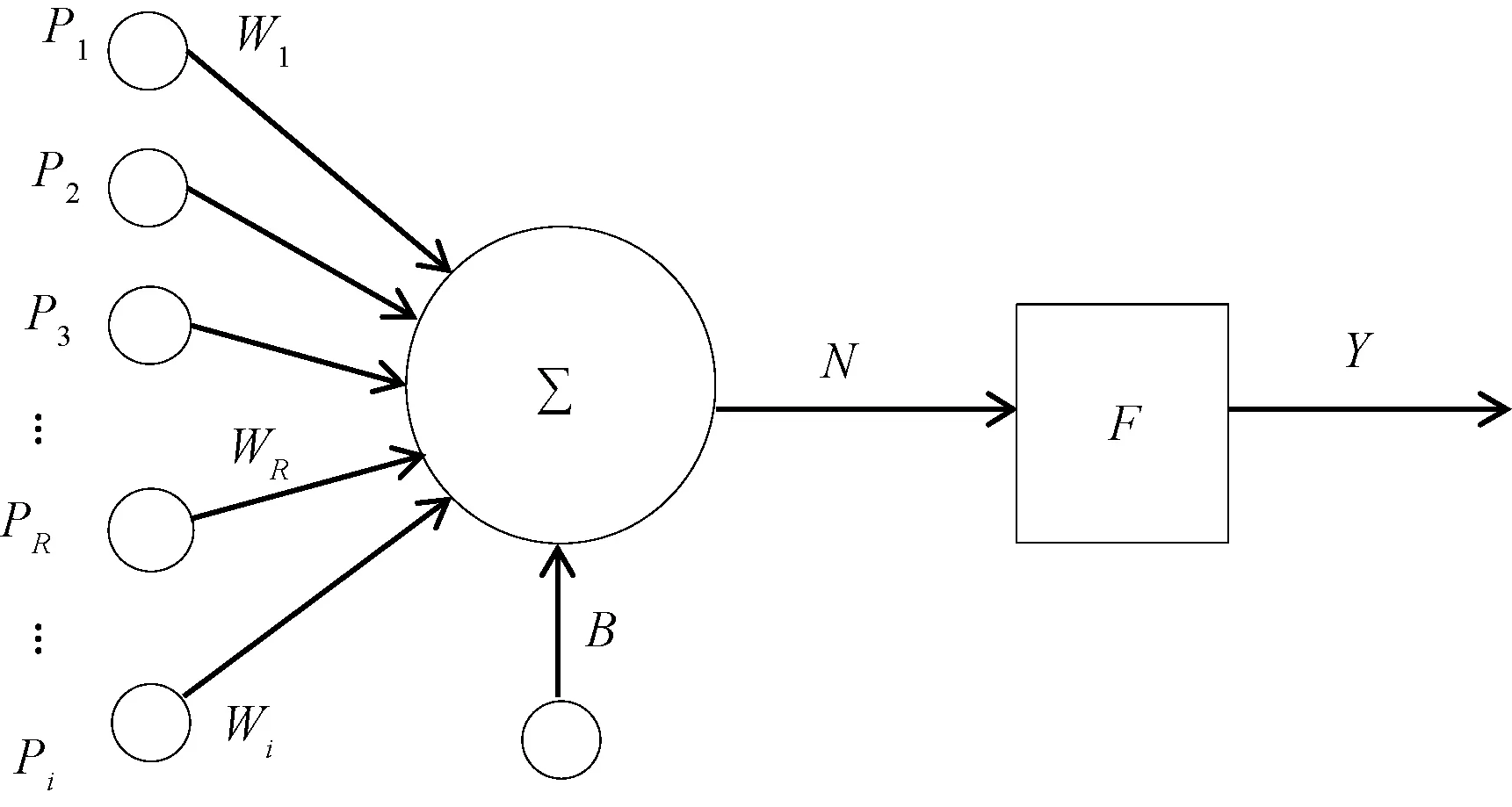
图1 基本的BP神经网络模型Fig.1 Basic BP neural network model

图中PR为该模型输入层的第R个神经元，权值WR负责连接前后2层网络中的神经元，i为输入层神经元的个数，N为所有神经元输出的累积，B为网络的阈值，传递函数F定义了网络的输入层向输出层的转换方式，Y为网络最后的输出，可以用下式表示：

Y=F(∑WR∑PR+B)

运用神经网络对纱线的成纱质量进行预测时，还有一个问题需要注意，由于神经网络输入层的输入变量单位不同，加上各神经元的数据还会相差若干个数量级，如果直接对原始数据进行神经网络训练很容易出现信息丢失和计算不稳定的情况，因此，在进行神经网络预测前，有必要对收集来的原始数据进行标度，进行统一的标准化处理，从而使最后数据的精度达到预先设定的要求，并在一定程度上提高神经网络的训练效率[7-8]。本文在构建神经网络前用logo函数对原始数据进行归一化处理。

本文数据来自山东某纺织厂的原棉物理指标及细纱质量指标，棉纱均在相同的生产条件(成纱的工艺配置和温湿度)下纺制。首先构建2个预测模型——纱线断裂强力模型和条干CV值模型(2个模型除输出参数不同外，输入参数和网络的结构均保持一致)，然后用MatLab分别构造1个单隐层的三层BP神经网络和1个双隐层的四层BP神经网络，通过同步训练和仿真，完成2个模型的预测实验，并通过实验结果比较这2种网络结构性能的优劣。

本文筛选出50组数据作为2种不同网络的训练样本，10组数据作为仿真时的检验样本。表1示出本文使用的部分数据。

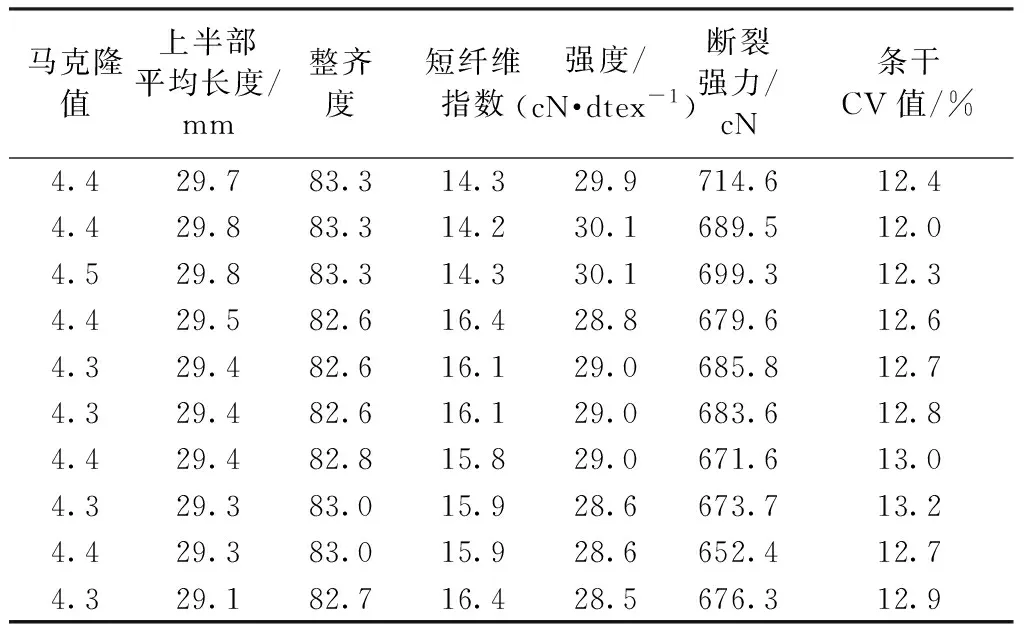
表1 部分原始数据Tab.1 Partial raw data

1.1 三层BP神经网络的设计

本文在进行棉纱断裂强力和条干CV值预测实验过程中，2种模型下的三层BP神经网络均采用如图2所示的神经网络结构。输入层有5个神经元，和1个网络输出单元，网络隐含层的神经元的个数S可由经验公式[9]给出。

式中s为输出层神经元个数。通过上式最后可运算求得隐含层的神经元个数S为4个，所以最后网络的结构为5-4-1。

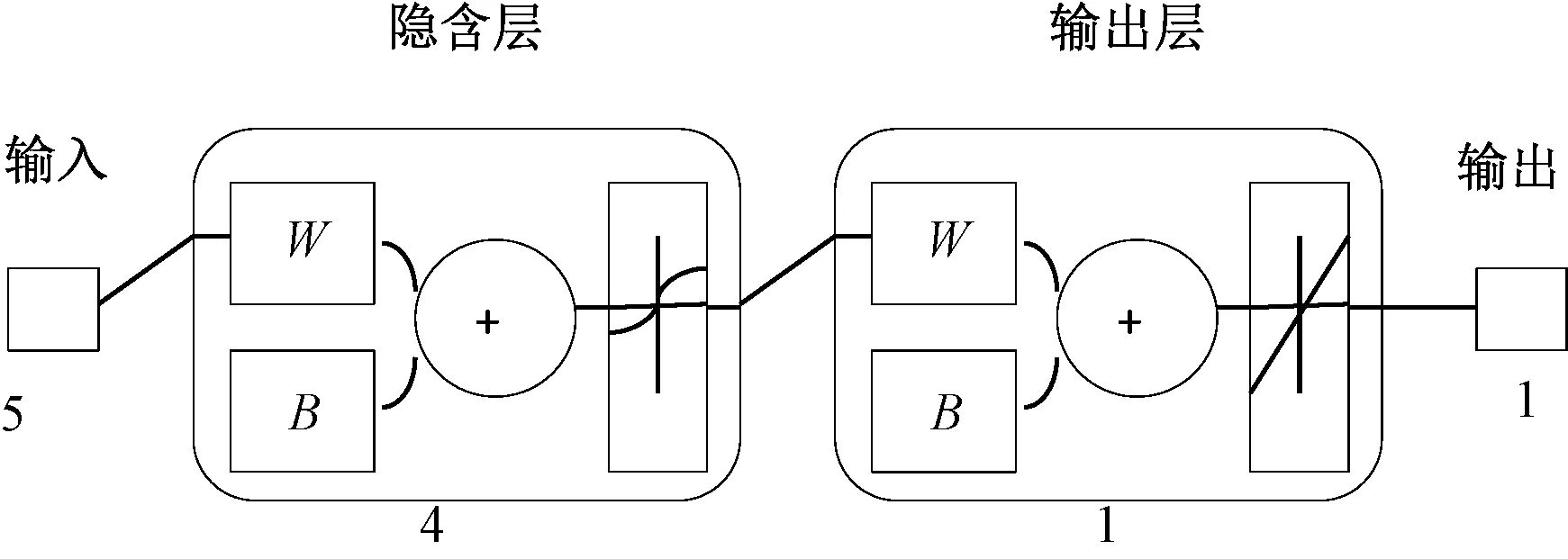
注：W为网络中的各神经元权值矩阵；B为网络的阈值。图2 三层网络结构Fig.2 Three layer network structure

1.2 四层BP神经网络的算法与设计

1.2.1四层神经网络的算法步骤

首先设定相关参数如下：P为总体样本数；i为输入层神经元数；n为第1个隐含层的神经元数；m为第2个隐含层的神经元数；s为输出层神经元数；x为网络的输入参数，x1为第1个隐含层的输出；x2为第2个隐含层的输出；y为输出层的输出；d为网络的期望输出；wi为输入层和第1个隐含层的连接权值；wn为第1个隐含层和第2个隐含层的连接权值；wm为第2个隐含层和输出层的连接权值；θ1为第1个隐含层的阈值；θ2为第2个隐含层的阈值；θ3为输出层的阈值；E为网络的误差。具体算法步骤如下。

1) 初始化权值wi、wn、wm。

2) 逐个输入P个样本。

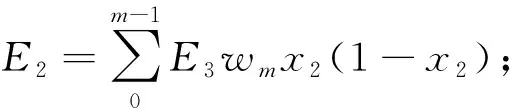
5) 学习训练完所有样本后依照权值修正公式进行各层权值的修正。

6) 输入新的权值重新进行各层输出和反传误差的计算，直到满足设定的精度目标值或达到预定的最大学习步数即终止学习。

1.2.2四层神经网络的设计

万能逼近定理虽然已经证明任意的m维到n维的映射只需要三层网络就可以完成，但是针对具体的不同的模型，就不能确定三层神经网络就是最合理有效的网络结构了。虽然层数的增加会使网络的结构变得冗杂，但是其减小误差的能力也会随之提升，因此可提高网络运算的精度，甚至在解决诸如预测纱线强力此类的输入和输出单元数较少的简单问题中，只要找到合理的隐含层单元数和恰当的训练函数，就可以提高训练效率。

为此，本文将设计含有2个隐含层的四层BP神经网络来构建棉纱的断裂强力和条干CV值的预测模型。依据选择隐含层神经元个数的经验公式[10]，在经过多次的的学习训练和对比分析，得到较为合理高效的四层神经网络的结构，其拓扑结构如图3所示。第1个隐含层由3个神经元组成，第2个隐含层包含2个神经元，最后的网络结构为5-3-2-1。

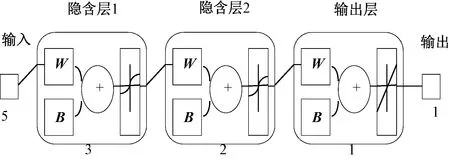
图3 四层网络结构Fig.3 Four-layer network structure

2 训练与仿真

2.1 纱线断裂强力模型

在设定好三层神经网络和四层神经网络的参数和结构之后，接下来将进行纱线断裂强力预测模型的训练和仿真实验。

2.1.1三层网络

本文采用MatLab提供的神经网络工具箱来进行棉纱断裂强力模型和后面的条干CV值模型的学习和训练。相关参数确定如下。

第1层的传递函数：tansig函数;第2层传递函数：purelin函数;学习函数：traigdm函数;三层网络的训练步数设定为10 000，训练目标设定为0.001，2次显示之间的训练步数为50。

训练得到的误差变化曲线如图4所示。

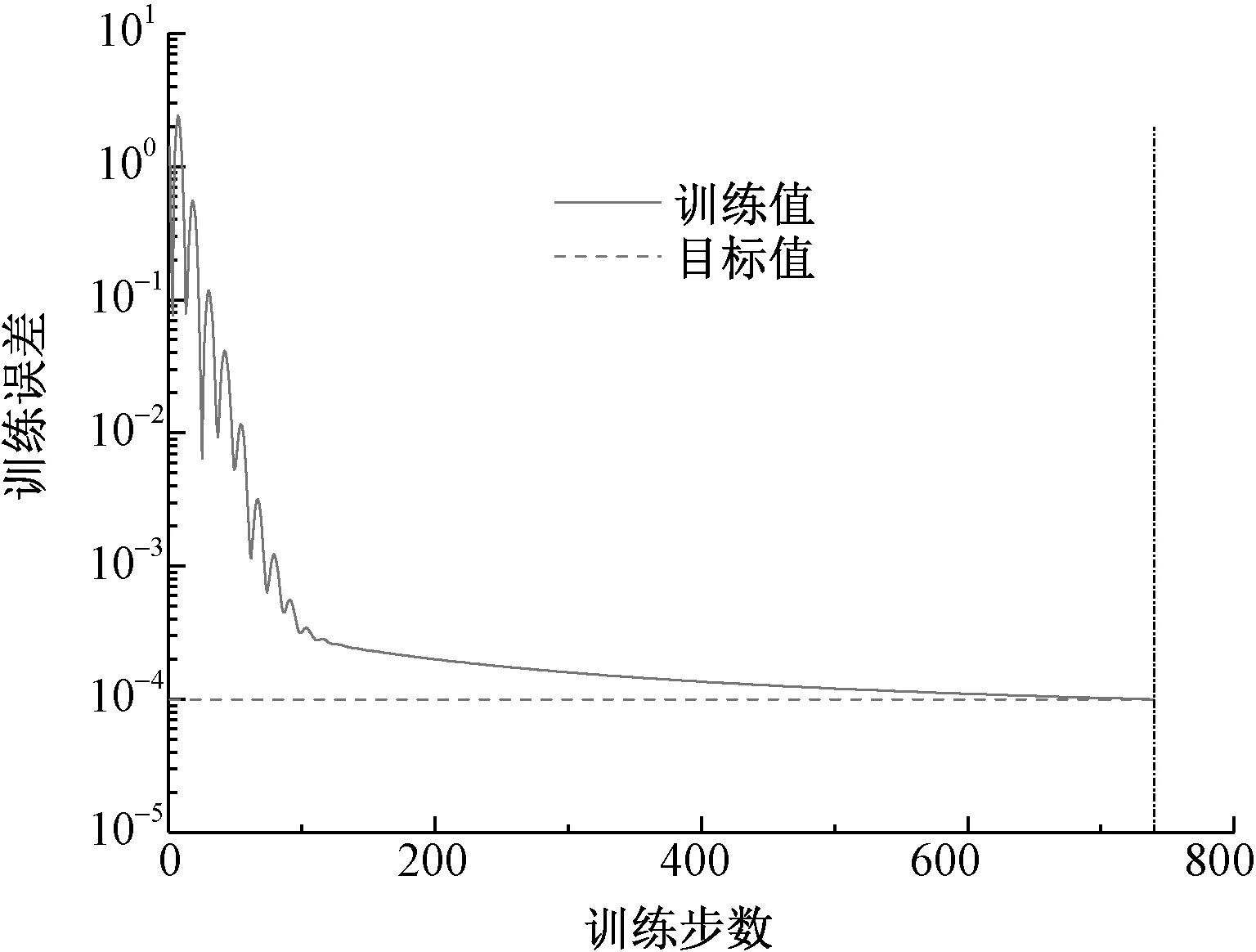
图4 纱线断裂强力模型三层网络误差曲线Fig.4 Three-layer network error curve of yarn breaking strength model

从图4可看出，该模型下三层网络的训练步数为740步，也就是网络的误差在此处达到目标值。

2.1.2四层网络

在同一个预测模型下，为保证实验结果的可比性，四层BP神经网络的相关参数与三层BP神经网络的参数设定保持一致。通过训练得到该神经网络的误差变化曲线，如图5所示。四层BP神经网络纱线断裂强力模型训练误差在第533步达到设定值。

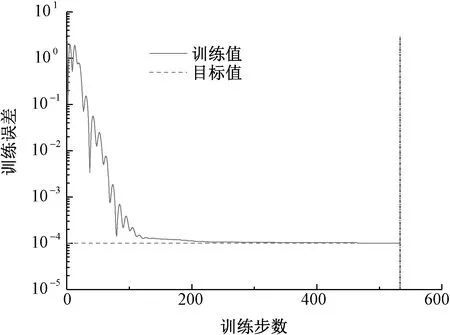
图5 纱线断裂强力模型四层网络误差曲线Fig.5 Four-layer network error curve of yarn breaking strength model

2.2 条干CV值模型

条干CV值预测模型的训练和仿真同样是在设定好单隐层的三层BP神经网络和双隐层的四层BP神经网络的参数和结构之后进行的，考虑到本文实验比较分析的是隐含层的层数对网络性能的影响，所以在条干CV值模型下网络的输入参数可以与纱线断裂强力模型所使用的数据相同，只是此时网络的输出参数由纱线断裂强力值改变为棉纱的条干CV值。

2.2.1三层网络

通过三层BP神经网络对该条干CV值模型进行仿真实验，得到的误差变化曲线如图6所示。可看出，该模型下的三层神经网络需要经过929步才能达到目标值。

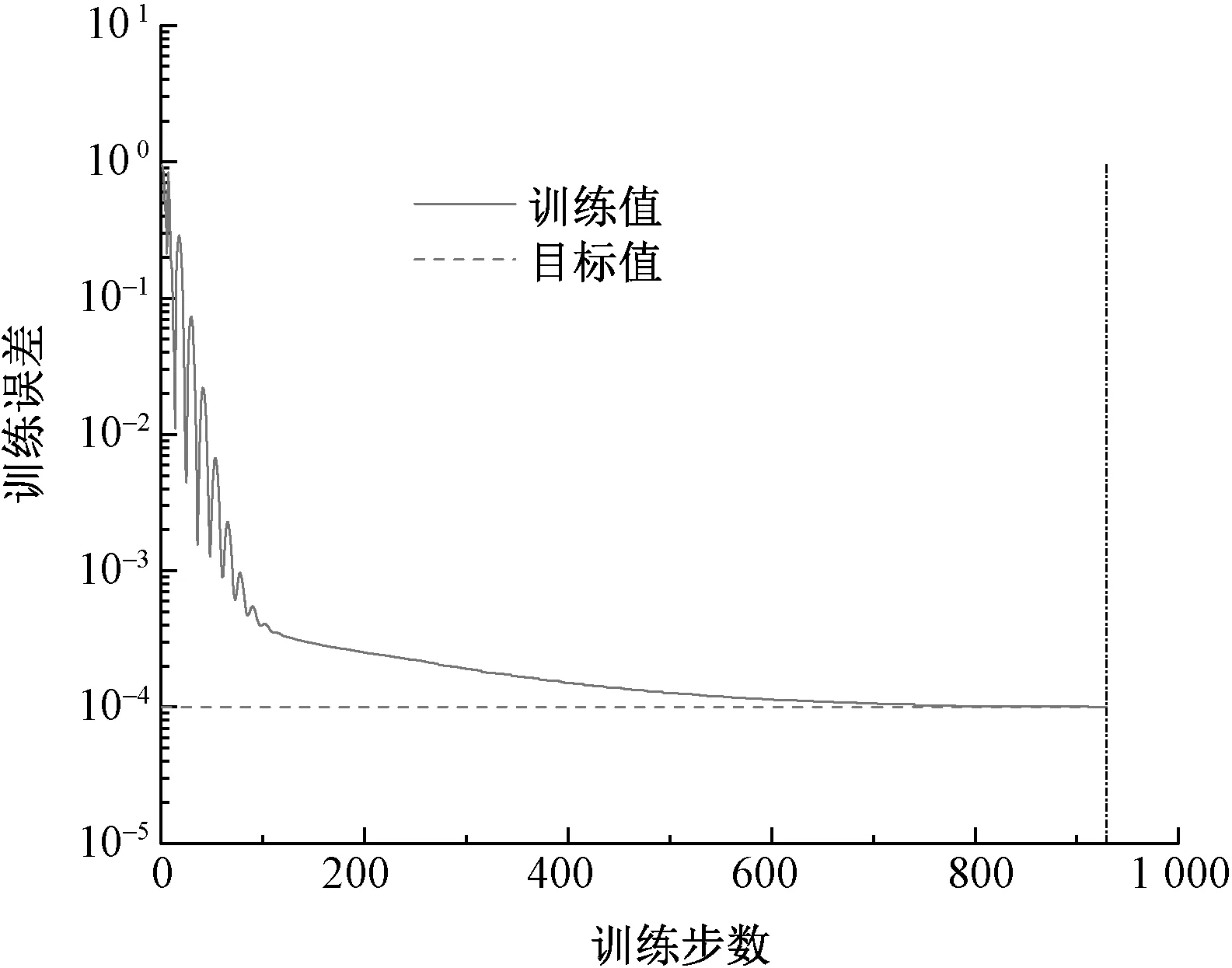
图6 条干模型三层网络误差曲线Fig.6 Three-layer network error curve of yarn levelness

2.2.2四层网络

通过四层BP神经网络对该条干CV值模型进行仿真实验，得到误差变化曲线如图7所示。可看出，网络误差在训练的第604步达到目标值。

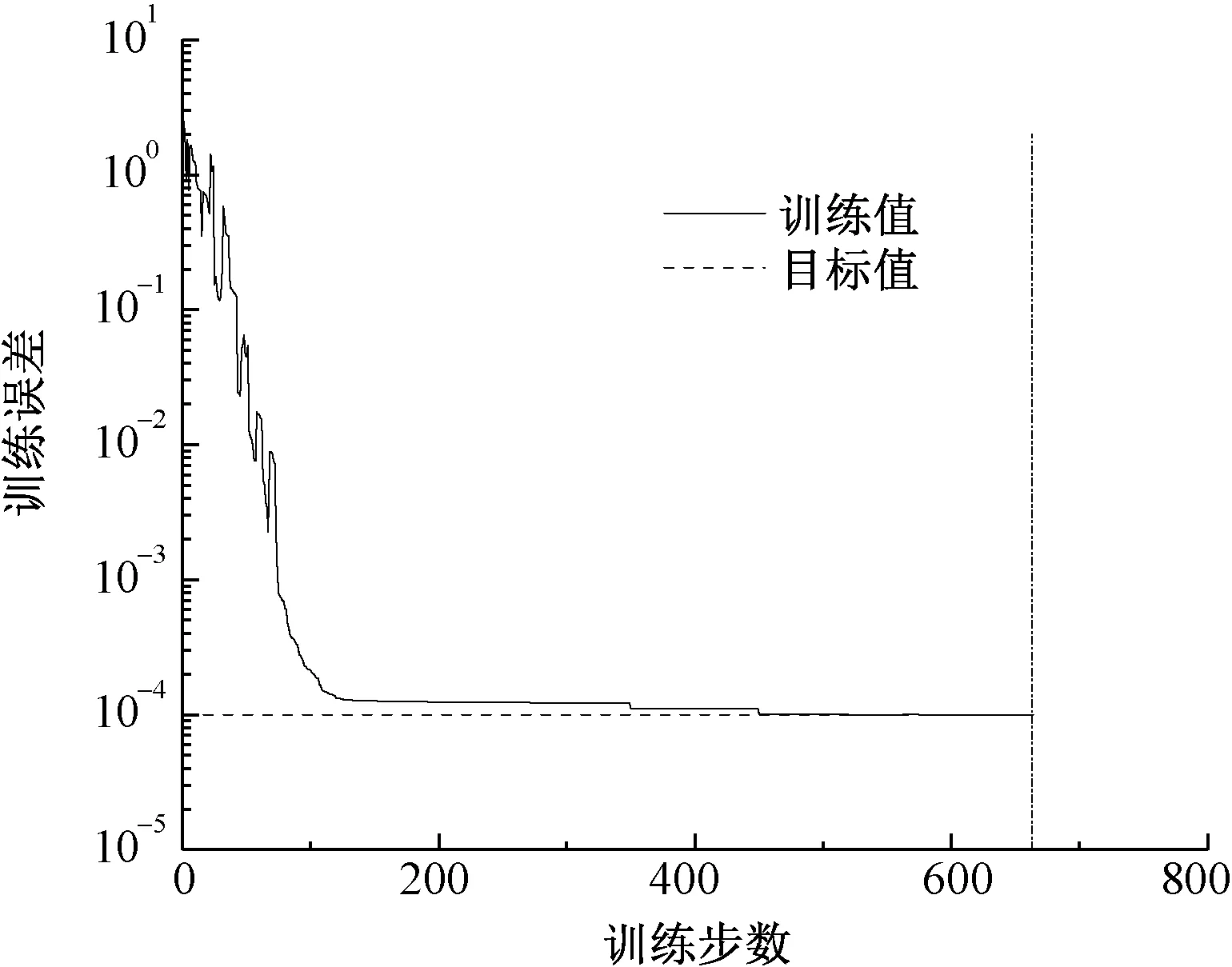
图7 条干模型四层网络误差曲线Fig.7 Four-layer network error curve of yarn levelness

2.3 仿真结果

通过三层BP神经网络和四层BP神经网络对棉纱断裂强力模型和条干CV值模型的预测和仿真，在设定好相同的误差精度目标后，得到各自的最大训练步数和最后的相对平均误差，其仿真结果如表2所示。显然，相比于三层BP神经网络，四层神经网络在效率和误差减小方面都有所提高。

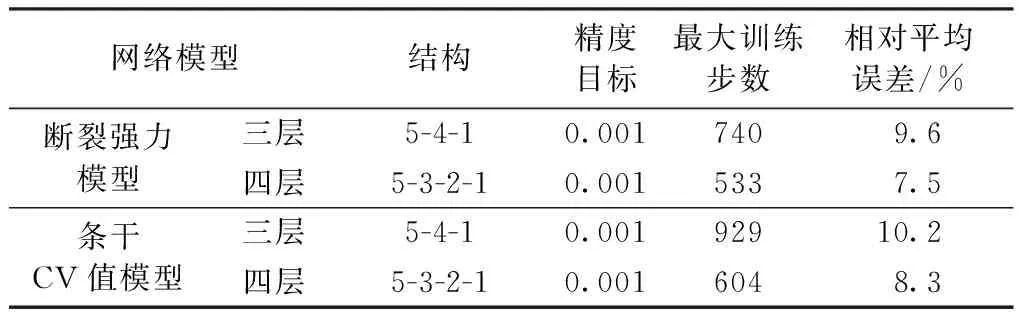
表2 仿真结果Tab.2 Simulation results

通常，在运用神经网络来进行质量预测模型的训练和仿真时，真实的实测数据和神经网络的预测值之间的接近程度会使用拟合度来进行标度。根据2组模型的仿真结果，利用MatLab工具箱对最终的数据进行相关性分析，结果如图8所示。

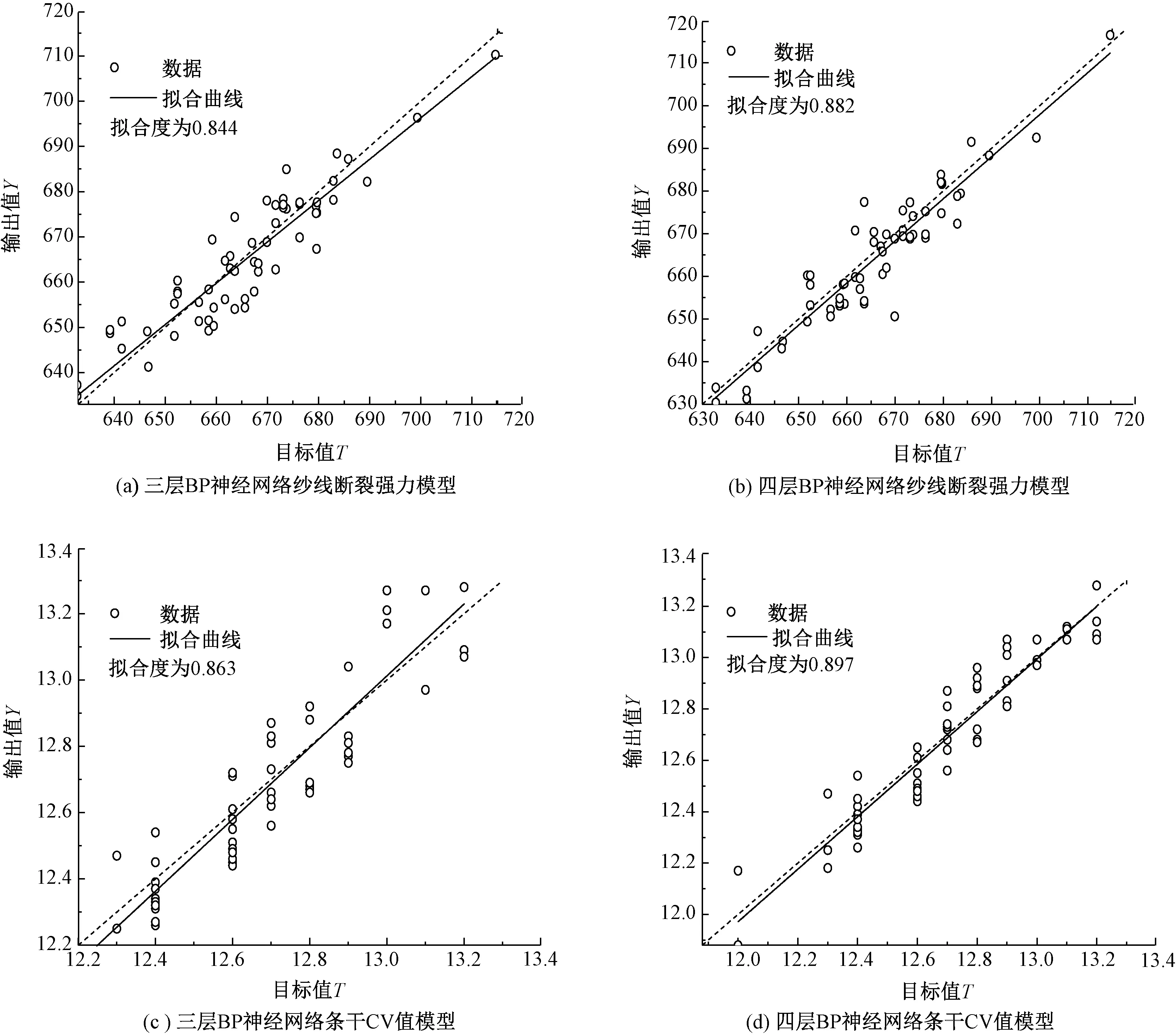
图8 相关性分析图Fig.8 Correlation analysis. (a) Three-layer BP neural network yarn breaking strength model; (b) Four-layer BP neural network yarn breaking strength model; (c) Three-layer BP neural network yarn levelness CV value model;(d) Four-layer BP neural network yarn levelness CV Value model

从图8可看出，三层BP神经网络纱线断裂强力模型的拟合度为0.844，四层BP神经网络纱线断裂强力模型的拟合度为0.882；三层BP神经网络条干CV值模型的拟合度为0.863，四层BP神经网络条干CV值模型的拟合度为0.897。以上分析说明，具有双隐层的四层BP神经网络相比于三层的BP神经网络，其预测值与实测值的一致性更高。

3 结 论

本文通过设计具有2个隐含层的四层BP神经网络对棉纱的断裂强力和条干CV值进行预测，并与三层网络的仿真结果进行比较，得到如下结论：虽然层数的增加使得神经元总数增加，网络的结构变得更加复杂，但四层网络的训练步数反而比三层网络的少，而且平均相对误差也要小，网络也更加稳定。说明将四层BP神经网络用于纱线质量预测是合理可行的，可在实际的生产活动中具有指导意义。

FZXB