面向控制的汽油直喷发动机轨压系统建模
刘文宪 滕 勤 张 华
(1-合肥工业大学汽车与交通工程学院 安徽 合肥 230009 2-安徽公安职业学院信息网络安全监察系)
引言
与进气道燃油喷射(PFI)相比,汽油直喷(GDI)不存在进气道湿壁效应,避免了进入气缸的燃油滞后和冷起动过量供油,发动机不仅冷起动快及相应的排放降低,而且瞬态响应好、瞬态空燃比控制精度高。此外,较高的喷油压力有利于燃油雾化,混合气质量得以改善。研究表明,汽油喷雾油滴的蒸发冷却作用,使充量系数和热效率提高且爆燃倾向降低[1-2]。但是,这引入了一个附加的轨压控制回路,使控制难度增大。而且,GDI发动机的轨压系统是一个具有强扰动的复杂非线性动态系统,共轨压力的波动将导致喷油器的喷油特性变化,使实际喷油量与期望喷油量出现偏差,燃烧室内的混合气特性也随之改变[3-4]。因此,轨压控制的稳定性是燃油量精确控制的根本保障。
由于高压油泵与发动机存在最佳的匹配关系,如果采用功率较大的高压油泵,虽然低速时能够产生较高的喷油压力,但会造成高速时能耗过大,故而最大泵油量通常按照最大燃油需求量来设计。由于油泵转速和泵油量随发动机转速而增大,且泵油效率也随转速而改变。因此,为了既保证起动时的轨压快速建立和低速时的燃油雾化性能,又要使轨压波动尽量小并在供油量需求最大时仍能足够快地改变喷射压力,且避免高速时过高的轨压导致燃油系统高压部件损坏和喷油量难于控制的问题,轨压控制变得极为重要。
轨压控制软件设计通常采用基于模型的方法,其优势在于:借助于闭环离线仿真,可以对策略与算法进行早期验证,而且可以通过直接代码生成,大大缩短软件编程时间和开发周期,构建一个面向控制的GDI发动机轨压系统模型则是其中的一个重要环节。
目前,面向控制的GDI发动机轨压系统的建模大多用于控制器设计与仿真,最常见方法是用商用仿真分析软件,如GT-SUITE、Modelica、AMESim等,选择封装好的模块并进行连接,设定相关的参数后自动生成模型[5-7]。这类模型精度较高,但不便于生成微控制器的控制代码。也可以基于流体动力学原理,通过一组微分方程和非线性静态方程来建立物理模型[8]。为了简化模型,可以根据轨压的阶跃响应特性,将系统描述成一阶线性系统与扰动的组合,只考虑控制输入与轨压变化率的关系,而其它非线性影响因素均作为扰动,这需要设计主动抗扰控制器来抑制强烈的扰动[9]。当忽略系统的动态特性时,常常采用回归分析方法,利用稳态实验数据拟合一组多项式静态模型来计算平均轨压[10-11]。
本文按照GDI发动机高压燃油系统物理结构和各部件的连接关系,基于燃油流量连续性方程和压力微分方程建立轨压系统动态数学模型,并利用MATLAB/SIMULINK搭建面向控制的轨压预测模型。分别利用发动机转矩和转速突变时的轨压阶跃响应数据对模型进行检验,评判模型的精度、跟随性和稳定性。
1 汽油直喷发动机轨压系统
1.1 轨压调节原理
GDI发动机燃油系统如图1所示,由电动燃油泵、高压油泵、高压电磁阀、高低压油管、共轨管和喷油器等组成。高压油泵由发动机凸轮轴上油泵凸轮通过挺柱驱动,泵油量取决于凸轮升程,由一个电磁溢流阀调节。当电磁阀断电时,燃油溢流回到低压油路;当电磁阀通电时,溢流回路关闭。油泵内部柱塞的运动使燃油压力升高,当油压大于导轨内压力时,燃油通过油泵出油口和高压油管进入高压燃油导轨。当导轨内部压力大于设定的最大压力时,燃油通过油泵内的限压阀流回油泵。ECU通过控制电磁阀的闭合时间,改变压油始点和压油行程来调节高压油泵输出油量和压力。
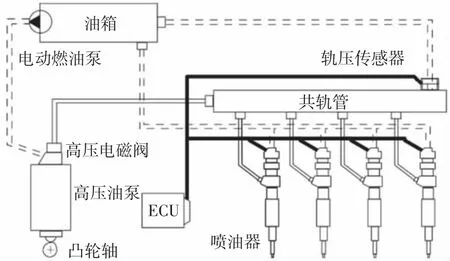
图1 GDI发动机燃油系统
1.2 轨压控制的基本结构
GDI发动机的轨压控制结构如图2所示,采用前馈+反馈的控制方式,控制输出是对应于泵油持续角度的电磁阀闭合持续时间。目标轨压由发动机转速和转矩需求确定,包括不同运行模式的map选择、范围与梯度限制,其中,需求转矩由转矩模型计算。前馈控制器用于提高控制的响应性,包括静态补偿和动态补偿两部分,前者的使能条件由发动机转速、目标喷油量、目标轨压、发动机启动结束后的时间和燃油温度来判定,控制增益根据目标轨压、目标喷油量和发动机转速确定;后者的使能条件是发动机启动结束后的时间,根据发动机转速与前后两次目标轨压变化量确定控制增益。反馈控制器采用PI算法,用来消除稳态偏差和扰动影响并防止超调,参数由轨压偏差、发动机转速和油温确定。基于轨压预测值轨压处理模块对测量轨压进行校验,防止轨压误判和消除振荡。轨压模型根据发动机转速、目标喷油量、泵油持续时间来计算轨压,其作用是:
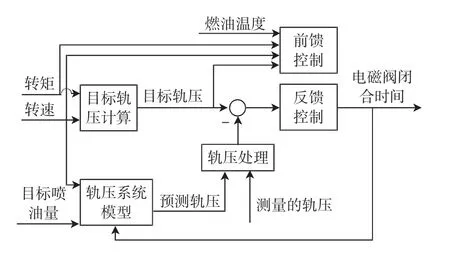
图2 轨压控制系统基本结构
1)提供闭环控制器所需的反馈信号或用其预测值对传感器测量的轨压进行校验;
2)当轨压传感器出现故障时,可以利用模型估计值进行故障模式下的安全保护控制;
3)作为虚拟被控系统,用于轨压控制策略和控制器的设计与仿真验证。
2 轨压系统数学建模
假设共轨系统各部分是刚性的,不发生形变。虽然燃油温度会引起燃油密度变化,进而引起燃油压力变化,但油温变化是一个缓变过程,所带来的是静态误差,对系统动态影响很小,且前馈控制器已经对油温变化进行相应的补偿,因此,建模过程中忽略了油温对油压的影响。根据质量守恒定律和流入、流出共轨系统的燃油相平衡的原则,得到图3所示的燃油流动图。
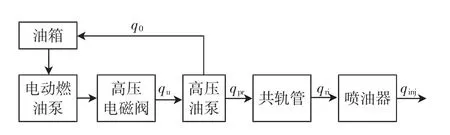
图3 轨压系统燃油流动图
2.1 高压油泵模型
高压油泵压油过程中,高压腔容积和压力随着柱塞行程而变化,导致燃油密度变化,考虑燃油的可压缩性,引入体积弹性模量。高压油泵输出油压与泵腔内容积变化量、流入与流出高压油泵的流量以及燃油泄漏量有关,其压力方程如(1)式所示[12]。

式中:Kf(pp)为高压泵内燃油体积弹性模量,MPa;pp为柱塞腔内压力,MPa;Vp(θ)为柱塞腔容积,m3;Ap为柱塞截面积,m2;hp为柱塞行程,m;ωrpm是凸轮轴转速,rad/s;qu和qpr分别是流入和流出高压油泵的燃油流量,m3/s;q0是燃油泄漏流量,m3/s。
流入高压油泵的燃油流量由低压燃油压力和泵腔内的压力决定,而油泵输出的燃油流量由泵腔内压力和共轨管内压力确定,对应的流量方程如(2)、(3)式所示。

式中:sgn是符号函数,确定燃油流动方向;U是开关函数,电磁阀开启时为1,关闭时为0;pd和pr分别是低压燃油和共轨管内压力,MPa;cpu和cpr分别是高压油泵入口和出口处的流量系数,无量纲;Apu和Apr分别是高压油泵入口和出口的有效截面积,m2。
2.2 共轨管模型
共轨管内压力由流入和流出的燃油量决定,其变化率为[13]:
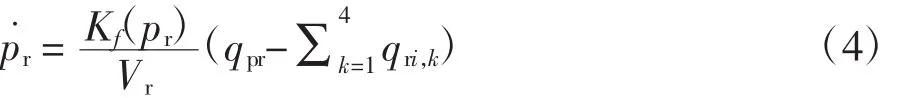
式中:Kf(pr)为共轨管内燃油体积弹性模量,MPa;qri,k为流入各个喷油器的燃油量(k代表喷油器编号),m3/s;Vr为共轨管容积,m3。
2.3 喷油器模型
喷油压力可以根据流入喷油器的流量、喷油量得到,流入喷油器的燃油流量可以根据共轨管压力和喷油器腔内压力计算,喷油量则根据喷油器腔内压力和缸内压力计算,如(5)~(7)式所示[14]。
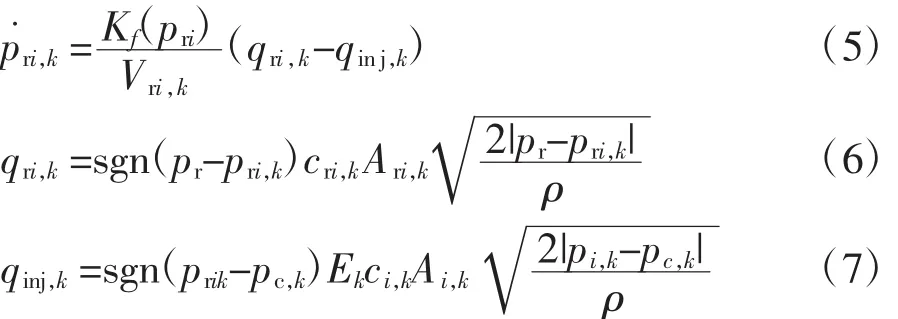
式中:Kf(pri)是喷油器内燃油体积弹性模量,MPa;Vri,k是喷油器腔内容积,m3;qinj,k是喷油流量,m3/s;pc,k是气缸压力,MPa;cri,k是喷油器入口流量系数,无量纲,Ari,k是喷油器有效进油面积,m2;ci,k是喷油嘴流量系数,无量纲,Ai,k是喷油嘴有效截面积,m2;Ek是喷油脉宽。
3 模型实现
为了简化起见,忽略燃油泄漏量,根据(1)~(3)式建立的高压油泵Simulink模型如图4所示,模型输入为发动机转速、电磁阀开关信号、共轨管压力,模型输出为高压油泵腔内压力和出口流量。由于低压燃油压力较为稳定,对轨压变化影响较小,故将其设为定值0.5 MPa。
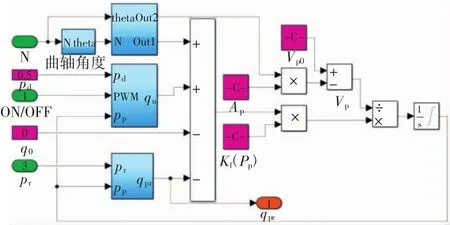
图4 高压油泵Simulink模型
根据(4)式建立的共轨管Simulink模型如图5所示,输入量为流入和流出共轨管的燃油流量,输出量为共轨管压力。
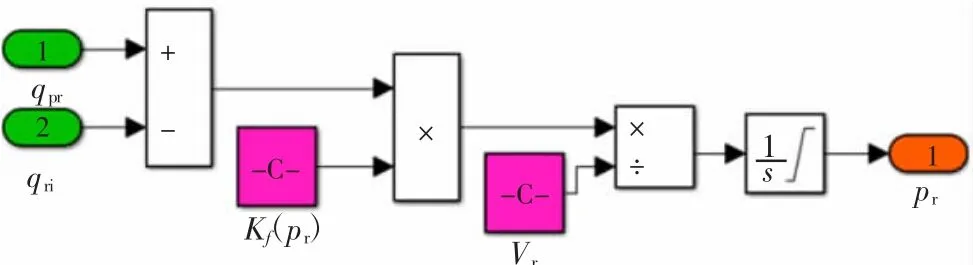
图5 共轨管Simulink模型
根据(5)~(7)式建立的喷油器 Simulink 模型如图6所示。模型的输入为共轨压力、气缸压力、转速和目标循环喷油量。通过转速确定循环时间,固定喷油正时,利用相应转速下的目标循环喷油量确定喷油脉宽。输出量为流入喷油器流量(提供给共轨管模型)和喷油器腔内压力。其中,气缸压力由发动机转速查取示功图MAP确定。

图6 喷油器Simulink模型
将以上子模型封装在一起,得到轨压系统Simulink模型如图7所示,输入为发动机转速、目标循环喷油量和泵油持续时间,输出为估计的轨压,模型的部分物理参数如表1所示。

图7 轨压系统模型

表1 轨压模型的部分参数mm
4 模型检验
4.1 试验装置与试验方法
为了获取验证模型所需的数据,在配置有冷却水恒温系统(AVL 553)和燃油恒温系统(AVL 753C)的AVL电力测功机(APA 202)试验台上,对一台1.5L GDI发动机试验,发动机主要参数如表2所示。分别使测功机工作在恒转速和恒转矩控制模式下,突变载荷和突变油门踏板位置,产生目标轨压的阶跃变化,通过总线接口模块ETAS ES590和INCA软件读取ECU中的控制与测量参数。
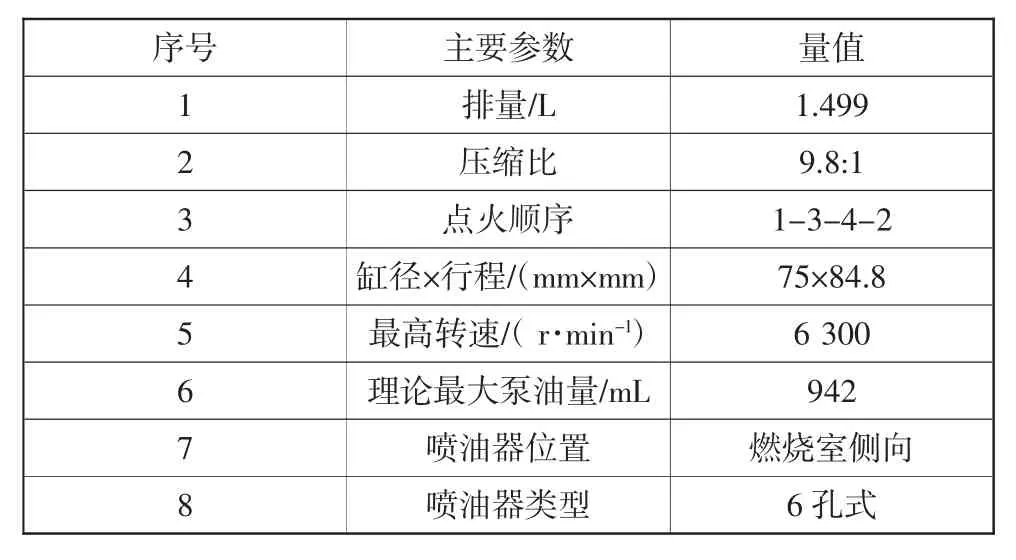
表2 试验发动机主要参数
4.2 负载突变试验
在发动机转速为2 000 r/min和转矩为11.8 N·m的稳定工况下,突然加大载荷,等待发动机稳定运行一段时间后,再突然减小载荷,发动机负载突变时的转速和转矩变化如图8所示。
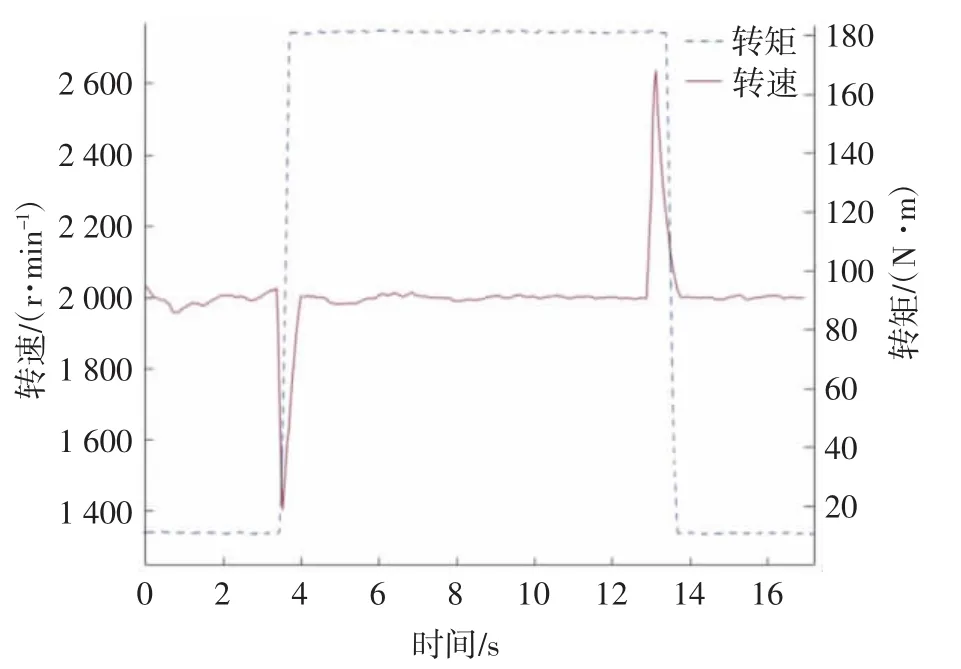
图8 负载突变时的发动机转速与转矩曲线
载荷突变时,发动机转速分别下冲到1 400 r/min和上冲到2 600 r/min,由于测功机控制系统快速调节油门,使ECU迅速将喷油量分别从5.2 mg/hub增加到39.8 mg/hub和从39.8 mg/hub减少到5.2 mg/hub以适应负载的变化,对应的发动机转矩迅速分别从11.8 N·m增至180.2 N·m和从180.2 N·m减至11.6 N·m,使转速恢复到初始状态。喷油量突变使得轨压从4.8 MPa到15.6 MPa和从15.6 MPa到4.9 MPa阶跃变化,如图9所示。

图9 发动机负载突变时的轨压阶跃响应
4.3 转速突变试验
在发动机转速为1 500 r/min和转矩为72.3 N·m的稳定工况下,突然开大油门,发动机转速快速提升到5 000 r/min;等发动机运行稳定后,再突然减小油门,发动机转速快速回到初始转速。对应的发动机的转速和转矩变化如图10所示。
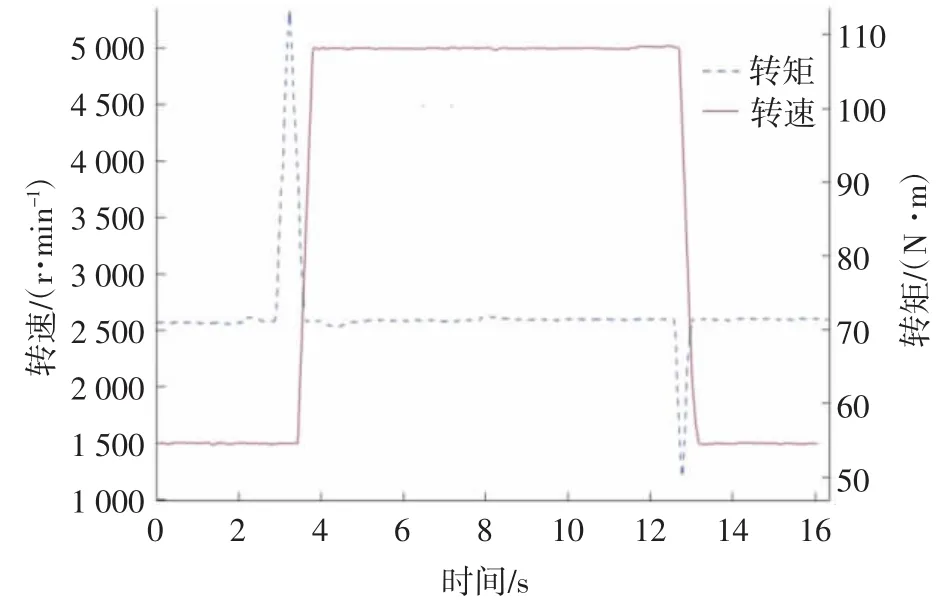
图10 转速突变时的发动机转速与转矩曲线
突然加速时,发动机转矩出现112.9 N·m的上冲峰值,这种过冲现象是由驾驶员转矩需求MAP中标定的调速特性和喷油量先升后降调节过程决定的,ECU先将喷油量从15.3 mg/hub快速增加到26 mg/hub,以保证发动机的加速性能;随着油门踏板开度的稳定和转速的上升,喷油量减少至18.5 mg/hub以防止飞车,使转矩稳定在72.5 N·m。突然减速时,减速断油使转矩出现50.1 N·m的下冲峰值,由于达到复供转速后恢复喷油,使转矩回升到72.3 N·m,此时喷油量为15.2 mg/hub。油门位置的突变分别形成轨压从7.6 MPa到12.8 MPa和从12.8 MPa到7.6 MPa的阶跃变化,如图11所示。
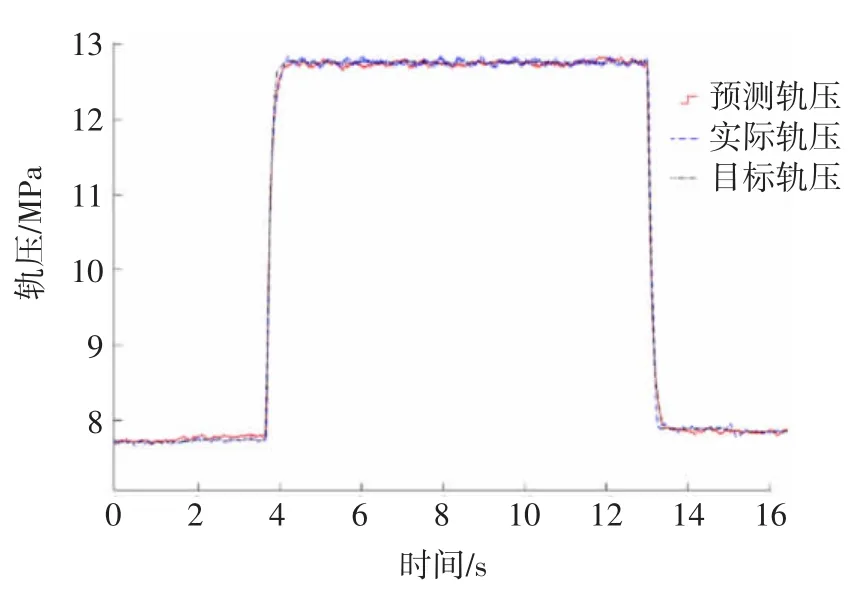
图11 发动机转速突变时的轨压阶跃响应
4.4 模型检验
4.4.1 模型精度按照(8)式计算模型拟合度R
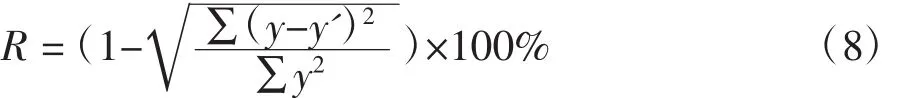
式中:y为测量的轨压,y'为计算的轨压。
负载突变时,轨压正、负阶跃响应的模型拟合度分别为98.46%和98.32%;转速突变时,轨压正、负阶跃响应的模型拟合度分别为99.15%和98.93%,表明模型具有很高的精度。建模过程中,将低压燃油压力、喷射正时都设定为定值并忽略高压油泵泄露量和油温的影响,未对模型精度带来显著影响。
4.4.2 响应性
响应性体现了模型对实测数据的跟随性能,利用上升时间来评价,定义为阶跃响应曲线上从稳态值的5%到95%所经历的时间。图9中的轨压正、负阶跃变化时,模型估计值的上升时间分别是0.61 s和0.58s,实测轨压的上升时间分别是0.57s和0.54s,均相差40 ms。图11中的轨压正、负阶跃变化时,模型估计值的上升时间分别是0.47 s和0.48 s,实测轨压的上升时间分别是0.46 s和0.45 s,分别相差10 ms和40 ms。
4.4.3 稳定性
模型的稳定性用从一个稳态进入另一个稳态后模型计算值与测量值的最大相对误差来衡量,在图9中负载突变时轨压正、负阶跃响应后的稳定阶段,模型计算值与测量值的偏差小于±0.42MPa和±0.12MPa,对应的最大相对误差分别为2.7%和2.5%。在图11中转速突变时轨压正、负阶跃响应后的稳定阶段,模型计算值与测量值的偏差小于±0.31MPa和±0.17MPa,对应的最大相对误差分别为2.3%和2.1%。
5 结论
针对GDI发动机高压燃油系统,基于燃油流量连续性方程和压力微分方程,建立了面向控制的轨压系统模型,并利用发动机台架上实测的轨压阶跃响应数据对模型进行了检验。
模型检验结果表明,无论是转速突变还是负载突变,轨压正、负阶跃响应时的模型拟合度均高于98%,模型预测值与实测值的上升时间之差均小于40 ms,不同阶跃响应稳态阶段模型计算值与实测值的偏差和最大相对误差分别小于±0.42 MPa和2.7%。表明模型具有良好的精度、动态跟踪性能和准确性。
在基于模型的控制中,所建模型不仅可用于轨压估计与预测、实时轨压的校验和诊断,而且可用于轨压控制策略和控制器设计时的在环仿真与验证。

