下尾风险与预期收益率的灾难敏感性——基于混合Copula模型的实证分析

熊海芳

(东北财经大学 金融学院，辽宁 大连 116025)

一、引言和文献综述

在投资活动中，相对于资产价格上涨，投资者更关注资产价格的下跌。在股市极端下跌时，投资者的这种偏好会更强。价格下跌主要是指收益小于零的情况，而极端下跌则是指罕见的灾难性崩溃。根据统计分布，价格下跌度量的是下行风险(downside risk)，极端下跌度量的则是下尾风险(left tail risk)。与下行风险关注市场下行时个股的风险不同，下尾风险则往往与股市极端下跌时个股的灾难敏感性有关，强调的是极端尾部事件[1]。那么，如何衡量个股在市场极端下跌时的风险敏感性？基于下尾风险的敏感性在个股预期收益中是否得到合理的风险溢价？本文将针对这些问题对中国的A股展开研究，这对于避免市场崩溃时的灾难风险有重要意义。

由于下尾风险关注的是发生频率较低的极端风险事件，可用的有效样本较少，如何对下尾风险进行估计就成了一个值得探讨的问题。相关研究对下尾风险的估计可分为截面数据角度和时间序列角度。以截面数据估计下尾风险的研究相对较少，Kelly和Jiang基于每一时期股票的横截面收益率采用幂律方法提取个股尾部风险的共同因子作为市场极端风险，个股的下尾风险则由其收益率对共同极端风险因子回归得到的系数来度量[2]。其他大多研究是基于个股与市场收益率时间序列对下尾风险进行估计，这种方法又可以分为两类：一是基于条件极值理论构造尾部贝塔；二是基于个股与市场收益率联合分布刻画个股与市场尾部相依结构进而估计下尾风险。Post和Versijp将尾部贝塔定义为当市场日收益率低于-10%时个股的市场贝塔[3]，Van和Zhou基于极值理论和条件VaR构造出个股的尾部贝塔[4]。基于条件回归、极值理论所得的尾部贝塔实质上为条件市场贝塔，这类估计方法最大的问题是只利用了满足某个条件的一小部分观测值，尾部贝塔的估计易受噪声值的影响，表现不稳健。Chabi-Yo等采用混合Copula模型描述个股与市场收益率的动态相依结构，通过对混合Copula模型进行估计从而计算出下尾系数，以下尾系数作为个股的灾难敏感性[1]。相对于极值VaR和条件回归法，Copula方法的优势在于它基于个股与市场收益率的联合分布，利用某段时间内个股与市场收益率的全部数据，保证收益率样本充足，同时可以滚动窗口估计，实现动态尾部风险估计，避免估计的尾部极值受到样本区间的严重影响。鉴于此，本文采用Copula方法对个股与市场收益率间的相依结构进行刻画，以估计出的下尾系数衡量个股的灾难敏感性。

对于个股下尾风险与预期收益率的关系，一些研究发现较高下尾贝塔的股票获得了较高的风险溢价，证实下尾贝塔是与下行贝塔不同的风险因子[1][2][5]。Weigert在全球40个国家中证实极端下尾风险在截面资产定价中有显著的作用[6]。这些研究证实了尾部风险对预期收益率的影响，并强调了尾部风险与下行风险的差异，但是他们采用了不同的尾部风险度量方法，有的仅考虑了下尾没有考虑上尾可能的影响。本文将在二元混合Copula模型衡量下尾风险的基础上进一步研究个股预期收益率的灾难敏感性，采用混合Copula的原因在于不同的Copula函数刻画不同的上尾或者下尾，采用混合Copula可以同时得到上尾和下尾风险敏感性，这样有助于控制上尾对下尾的影响。

国内对于尾部风险的讨论主要集中个股尾部和市场之间尾部关联的衡量问题上。但是，这些研究并没有从横截面上分析个股收益率对市场极端尾部的敏感性[7][8][9]。国内有关个股的灾难敏感性的研究较少且对下尾风险与收益率关系存在分歧：陈国进等和胡志军都借鉴Kelly和Jiang的研究方法，基于极值理论和尾部幂指数分布统计量对下尾风险进行衡量，发现股票的下尾风险因子载荷越大其超额收益率越高[10][11]，然而陈坚则发现基于极值理论构建的VaR在股票市场组合收益率回归中系数为负，基于Copula方法的VaR的预测效果并不十分显著[12]。

与国内现有研究相比，本文的创新处可能有以下几个方面：第一，从个股层面出发，采用二元混合Copula模型对个股与市场收益率的动态相依结构进行刻画，以计算出的下尾系数衡量个股下尾风险。现有研究或者围绕下尾风险的度量，或者刻画不同市场的尾部相依性，但较少从截面预期收益的敏感性角度研究个股与市场收益率间的下尾相依结构。第二，本文不仅考虑协偏度、协峰度等高阶矩以及下行风险的影响，区分高阶矩风险和下行风险与下尾风险的差异，还考虑下尾风险与上尾风险间的相互影响，控制上尾风险的作用。第三，本文设定了7个收益率观测期，预期收益率的检验范围由短期的1个月覆盖至长期的36个月。 这主要是考虑到下尾风险受到样本区间的影响具有时变性，在市场极端下跌时表现更明显，而罕见灾难性的影响通常会持续一段时间。

二、研究设计

(一)灾难敏感性的估计：尾部系数

(1)

参考Chabi-Yo等，下尾系数、上尾系数则由式(2)计算所得[1]：

(2)

1.二元阿基米德Copula函数

阿基米德Copula在刻画金融资产间非线性、非对称相关结构方面具有较好的效果[13](P28-30)，因此本文选择常见的二元阿基米德Copula函数刻画个股与市场的动态相依结构。二元阿基米德Copula分布函数的具体表达式如式(3)所示：

C(u,v)=φ-1(φ(u)+φ(v))

(3)

式(3)中，函数φ(·)称为二元阿基米德Copula函数的生成元，选择不同的生成元函数可以得到不同的阿基米德Copula函数。本文主要考虑Gumbel Copula、Clayton Copula及Frank Copula等三种常用的阿基米德Copula函数函数。Gumbel Copula函数具有非对称性，它对变量在分布上尾部的变化较敏感。Clayton Copula函数也可以用来描述变量间的非对称关系，但是Clayton Copula对变量的下尾变化较为敏感。Frank Copula函数的上尾、下尾相关系数均为零。为了更灵活的描述个股与市场收益率间的复杂相依结构，本文基于上述3类阿基米德Copula函数构建二元混合Copula模型，如式(4)所示：

C(u,v;Θ)=w1CG(u,v;θ1)+w2CCl(u,v;θ2)+(1-w1-w2)CF(u,v;θ3)

(4)

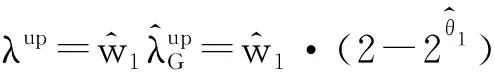
2.边缘分布的估计

(5)

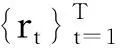
(6)

(二)相关控制变量

1.市场贝塔与非对称贝塔。个股的市场贝塔是根据过去1年个股减去无风险利率后的日超额收益率对市场日超额收益率进行回归后得到的。为了区分下行风险、上行风险两个非对称风险对尾部风险的影响，本文参照Ang等将下行贝塔定义为当市场日收益率小于其平均值时个股收益率对市场收益率回归的条件贝塔[16]；上行贝塔则与之相反。下行贝塔、上行贝塔的计算式分别如式(7)和式(8)所示。

(7)

(8)

式(7)和式(8)中，ri、rM分别为个股、市场扣除无风险收益率后的日超额收益率，μM为过去1年中市场日超额收益率的平均值。

2.协偏度与协峰度。协偏度计算方法如式(9)所示，协峰度计算公式如(10)所示。

(9)

(10)

ri=β0i+β1imkt+β2ismb+β3ihml+ei

(11)

式(11)中，mkt代表市场因子，smb代表规模因子，hml代表价值因子。

4.非流动性。本文以Amihud的非流动性指标ILLIQ作为个股流动性风险的代理变量[17]，ILLIQ计算方式如式(12)所示。

(12)

式(12)中，Di为个股i在过去1年内的交易天数，Pit为个股i在过去1年内第t个交易日的收盘价，DVOLit为个股i在过去1年内第t个交易日的交易金额。由于这样计算出的非流动性指标值过小，为了使得其更容易表述，本文将其扩大107倍。

(三)样本说明及数据来源

考虑到1996年12月后我国开始正式实施涨跌停板限制，本文选定样本区间为1997年1月至2018年1月，以在上海证券交易所上市、交易的股票作为研究样本，为了保证尾部系数估计的准确性，剔除年交易日不足100天的股票。由于本文尾部系数、部分控制变量的计算区间为1年，因此相关实证分析实际开始日期为1998年1月。本文以1年期定期存款利率作为无风险利率。本文样本数据全部来自国泰安金融数据库(CSMAR)。

三、实证结果分析

(一)下尾风险的时变性与市场崩溃

采用式(4)所示的混合Copula函数计算得到个股的尾部系数，基于月度数据，将所有样本股票的下尾系数进行流通市值加权平均，所得的下尾系数加权平均值即可视为该月市场的总体下尾系数。市场总体下尾系数与上证综指月收益率的走势如图1所示。

图1中，下尾系数明显具有时变特征，有3个区域的下尾系数相对较高，市场收益率在这些区间内出现了极端负值，分别将这3个区域标注为1、2、3。区域1中，下尾系数达到整个观测区间的峰值，它正好对应2008年全球金融危机时期。区域2对应的区间涵盖了2009年8月至2010年4月股市出现暴跌的月份；区域3包含了2次暴跌，一次是2015年8月股灾时期，一次是2016年1月熔断机制试行时所导致的恐慌性暴跌时期。总的来看，当市场总体下尾系数快速上行时，市场收益率倾向于出现极端负值，这说明下尾系数可以较为准确地捕捉到市场极端下尾事件，可以作为下尾风险的有效代理变量。

(二)按尾部系数分组的组合特征

表1展示了按照下尾系数、上尾系数分组后分别从风险特征、交易特征、公司特征3个角度对各子样本的描述统计。其中，“Low”表示尾部系数最低的一组，“High”表示尾部系数最高的一组，“H-L”表示最高组与最低组在某个特征上的差值。

图1 下尾系数(左轴)与市场收益率(右轴)

表1中以下尾系数分组后，从风险特征看，下尾系数与上尾系数表现出明显的负相关关系：个股的下尾系数越高，上尾系数越小。下尾系数较高的股票，其市场贝塔、下行贝塔较高，其上行贝塔则较小。协偏度、协峰度和特质波动都随着下尾系数的增大而减小。从交易特征角度来看，下尾系数与非流动性、月交易金额都不存在明显的单调关系；过去1个月收益率与下尾系数大致正相关，过去6个、12个月收益率与下尾系数呈显著负相关关系。从公司特征角度看，下尾系数越高的股票其流通市值越小，下尾系数与市盈率不存在单调关系。

表1中以上尾系数分组后，个股的上尾系数越大，其市场贝塔、上行贝塔越大；上尾系数与下行贝塔没有表现出明显的单调关系。上尾系数与协偏度表现出单调正相关关系，各组间协峰度则没有明显趋势。与下尾分组表现不同的是，以上尾系数分组后，各组的特质波动与上尾系数没有明显的单调关系。非流动性、月交易金额等交易特征与上尾系数没有明显的单调关系，过去1个月、6个月、12个月收益率与上尾系数均表现出明显的负相关关系。上尾风险高股票的流通市值较大，上尾系数与市盈率未呈现单调关系。

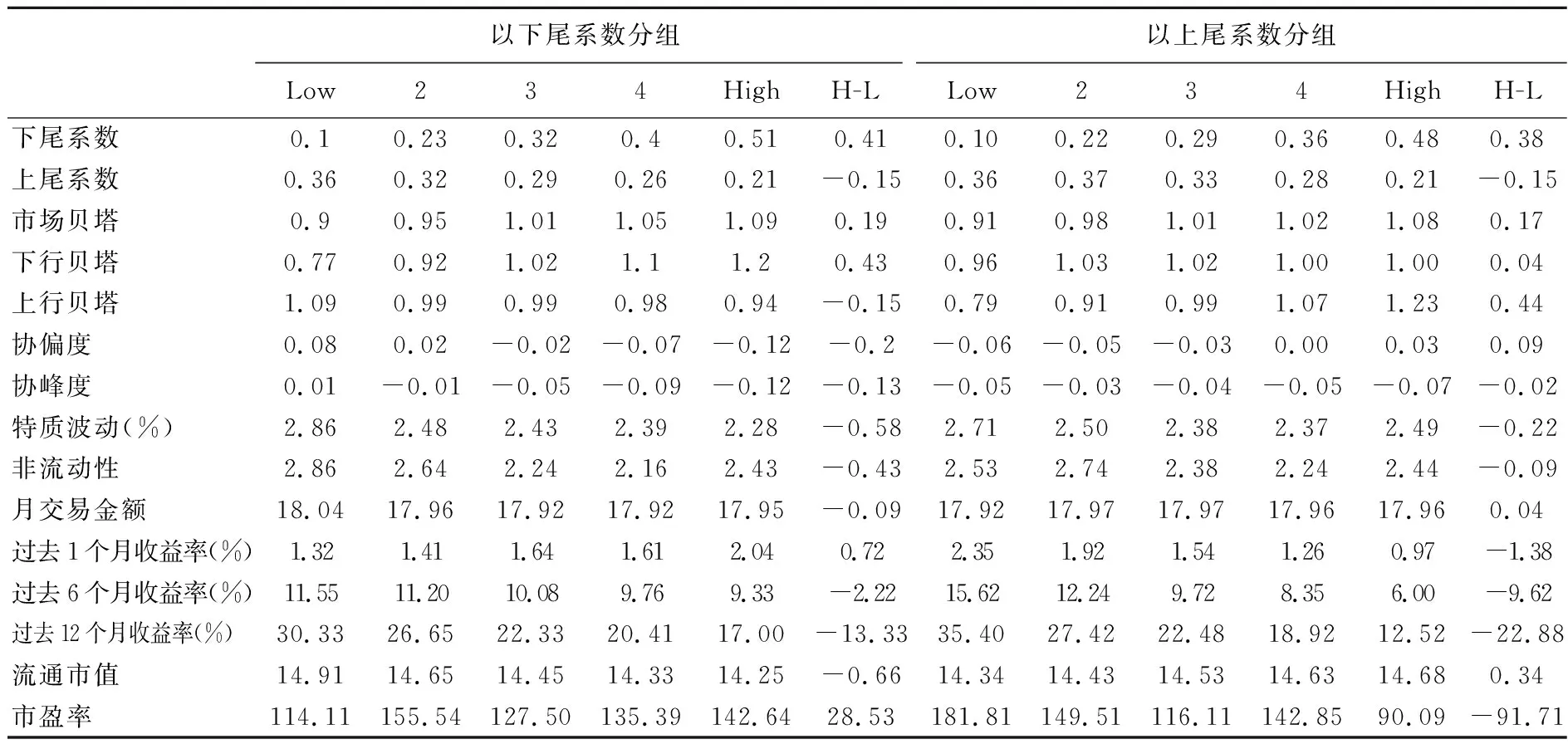
表1 描述性统计

注：公司流通市值、月交易金额均为公司实际流通市值、月交易金额取自然对数后的值。

(三)下尾系数与上尾系数的分组定价检验：组合价差法

本文采用单因子和双因子的组合价差法检验尾部系数的定价效果。在每个月，依据过去1年日收益率序列计算出个股的尾部系数，将个股按照其尾部系数进行排序分组，等分为5组。为了更加全面的展示尾部系数与预期收益率间的关系，本文设定7个收益率观测区间，持有期分别为1、3、6、12、18、24和36个月，计算各组合在给定计算区间内扣除无风险收益率后的平均月超额收益率，每月重新调整各组合。组合的构建期与持有期间隔1个月。

表2展示了以等权重方式计算组合收益率时，以下尾系数、上尾系数进行单因素分组后各子样本收益率表现。其中，“Low”表示尾部系数最低组，“High”表示尾部系数最高组，“H-L”为最高组减最低组。为了减小收益率自相关性与异方差性的影响，本文使用Newey-West调整后的t值。以流通市值加权的方式计算组合收益率时，不同预测期下各子样本收益率表现与等权重计算方式下基本一致，因此没有展示。

表2中个股以下尾系数分组后，未来1个月超额收益率与下尾系数有正相关关系，但下尾系数最高组和最低组间收益率差异不显著。将预测期拓展至3个月和6个月，收益率表现与1个月期类似。但是，随着预测期的延长，下尾系数最高组和最低组间收益率差异变得越来越显著。进一步对预期12个月、18个月、24个月和36个月的收益率进行分析，发现将观测期延长到未来1年及以上时，预期收益率与下尾系数表现出显著的正相关关系，下尾系数最高组和最低组间的收益率差异在1%的水平上显著。持有期为18个月是下尾系数多空对冲组合预期收益率走势的分水岭：在预测期为18个月以内时，随着预测区间的延长，下尾系数最高组和最低组间收益率差异不断扩大；随着收益率观测期提高至24个月、36个月，虽然下尾系数多空对冲组合收益率仍显著为正，但是其大小随着预测期间的延长逐渐衰减。

表2中个股按照其上尾系数分组时，在所有观测区间内，上尾系数最高组的收益率均低于上尾系数最低组，但两者差异不显著。与下尾系数分组类似，上尾系数多空对冲组合收益率绝对值随着观测区间的延长表现出了一定的上升趋势，并在1年半时达到最大值，随后组合收益率绝对值开始下降。各子样本收益率与上尾系数表现出不严格的单调负相关。这说明，上尾系数对股票预期收益率的解释能力比下尾系数的解释能力差。

表2 单因素分组后组合收益率 (单位：%)

注：(1)*、**、***分别表示10%、5%、 1%水平上显著；(2)括号内是经Newey-West调整后的t值。下表同。

表2中，在观测期为1年半(18个月)时，尾部系数多空对冲组合收益率绝对值达到最大，以等权重方式、流通市值加权方式计算的组合收益率差异不大，因此，本文设定观测期为1年半(18个月)，以等权重方式计算各组合收益率。尾部系数的双重分组结果如表3所示。

表3中Panel A展示了控制上尾系数后，以下尾系数分组后各子样本收益率表现。在各上尾系数组，股票预期收益率都与下尾系数表现出单调正相关关系，下尾系数最高组和最低组收益率差异均在1%的水平上显著，即控制了上尾风险后，下尾风险对预期收益率的影响比较稳健。随着上尾系数的增大，下尾系数多空对冲组合收益率随之减小，这印证了上尾系数与下尾系数的负相关关系。控制了下尾系数后，以上尾系数分组后各子样本表现如表3中Panel B所示。控制下尾风险后，上尾系数最高组与最低组间收益率差异相对于表2中上尾系数单因素分组(18个月)差异更小且不显著，预期收益率与上尾系数不再表现出负相关关系。由此可见，在控制了尾部风险相互间影响时，下尾系数与预期收益率间正相关关系保持稳健，下尾风险大的股票能够获得更高的超额收益率，而上尾系数与预期收益率不再存在相关关系，这说明下尾风险可以解释股票的横截面预期收益率，而上尾风险则对股票收益率影响不大。

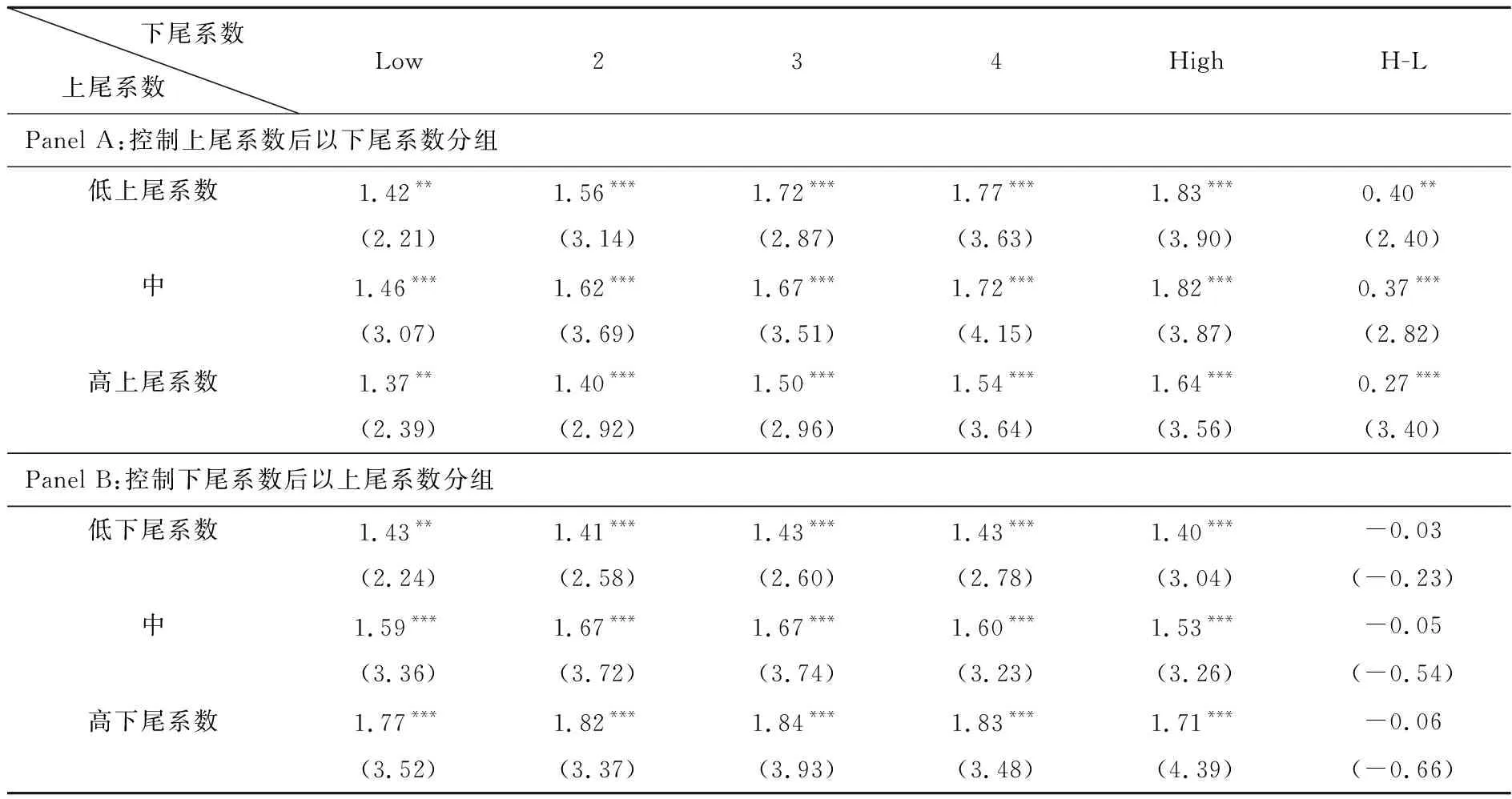
表3 下尾与上尾系数双重分组的各子样本收益率 (单位：%)

(四)下尾系数与特征因素的双重分组检验

1.下尾系数与风险特征。Ang等发现高下行贝塔能获得更高风险回报[16]，Harvey和Siddique证实系统性偏度在截面资产定价中有重要作用[18]，Fang和Lai证实协峰度能得到正确定价[19]。Ang等还发现股票的特质波动与预期收益率之间存在负相关关系[20]。鉴于此，本文加入市场贝塔、下行贝塔、协偏度、协峰度、特质波动等因子，将这些风险特征因子与下尾系数分别进行双重排序分组，从而检验在控制这些风险特征后高下尾系数股票是否仍能获得高预期收益率(表4)。

表4中Panel A展示了市场贝塔与下尾系数双重分组结果。在控制了市场贝塔后，股票预期收益率与下尾系数单调正相关关系保持不变，下尾系数最高组和最低组间收益率差异显著。下行贝塔与下尾系数双重分组后收益率结果如表4中Panel B所示。在控制了下行贝塔后，随着下尾系数的提高，各子样本预期收益率不断提高，且下尾系数最高组、最低组间差异仍在1%的水平上显著，这说明下行贝塔和下尾系数代表了个股不同的风险特征，下行风险不能解释下尾风险带来的风险溢价。表4的Panel C、Panel D和Panel E显示了高阶协矩、特质波动与下尾系数双重分组结果。与市场贝塔、下行贝塔分组结论类似，在控制了协偏度、协峰度和特质波动后，下尾系数与预期收益率仍保持了稳健的正相关关系。总体而言，下尾系数与股票预期收益率存在正相关关系，控制了市场风险、下行风险、高阶协矩风险和特质波动后，这种关系依然稳健。

表4 风险特征与下尾系数双重分组后子样本收益率 (单位：%)

2.下尾系数与动量因素。动量因素与下尾系数双重分组结果如表5所示。结果表明，在控制了过去1个月、6个月后，预期收益率随着下尾系数的提高而单调增加，多空对冲组合收益率显著大于0。控制过去12个月收益率时结果类似，在此不再赘述。

3.下尾系数与流通市值。流通市值与下尾系数双重分组实证结果如表6所示。表6中发现，在控制了流通市值后，下尾系数与预期收益率间正相关关系保持不变，高下尾系数组收益率显著高于低下尾系数组。在不同流通市值组，下尾系数多空对冲组合月平均收益率基本保持在0.22%，远小于表2中下尾系数单因素分组多空对冲组合(18个月)收益率0.43%。这证实规模因素在一定程度上干扰了下尾系数单因素分组的结果，强调了控制规模因素的重要性。

表5 动量因素与下尾系数双重分组后子样本收益率 (单位：%)

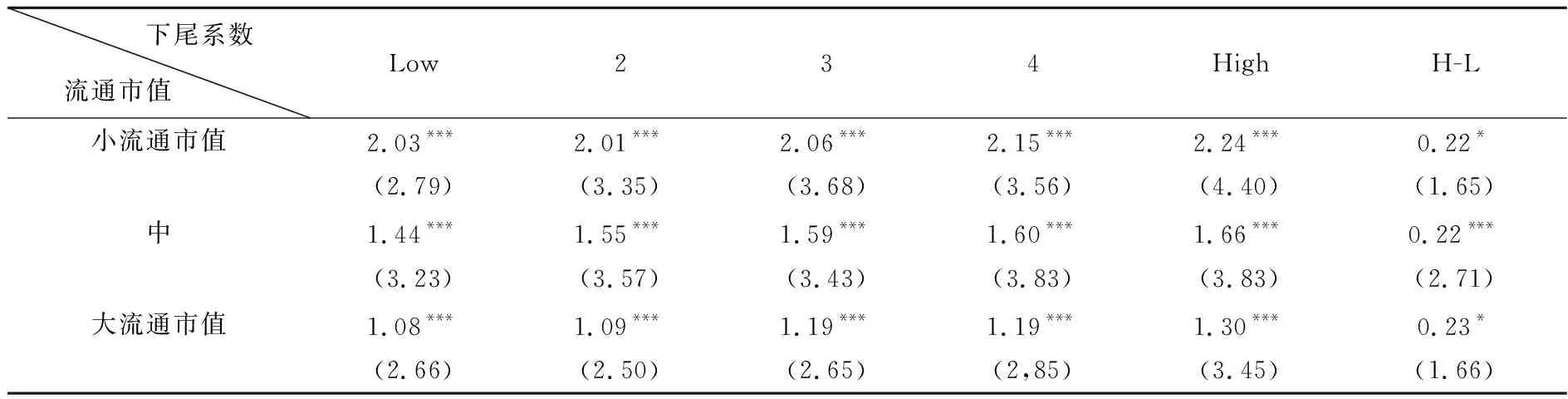
表6 流通市值与下尾系数双重分组后子样本收益率 (单位：%)

综上可知，控制风险特征、交易特征、公司特征等相关因素后，高下尾系数仍具有高预期回报率，说明下尾风险是不同于下行风险、高阶协矩等各种风险的一种非对称风险。

(五)下尾系数与预期收益率：Fama-MacBeth回归

以预期未来18个月平均超额收益率作为因变量，采用Fama-MacBeth回归将预期收益率对下尾系数进行回归，将前文讨论的风险特征、交易特征、公司特征三类共14个因素作为控制变量，逐步加入回归方程中，观察下尾系数显著性的变化。Fama-MacBeth回归结果如表7所示。

在表7的7个回归方程中，下尾系数对预期收益的参数估计值一直都显著为正，这说明下尾系数能够带来较大的预期收益率，不受到其他风险特征、交易特征和公司特征的影响，即下尾系数是与下行贝塔和高阶矩等因素不同的尾部敏感性度量。

为了从时变的角度考察下尾系数与预期收益率的关系，分别以不同的7个观测期内月平均超额收益率作为因变量，进行回归检验。由于下行贝塔与下尾系数有一定的相关性，所以选择表7中方程(6)进行回归，回归结果如表8所示。

在表8的7个收益率观测期内，下尾系数对横截面预期收益率都有显著的正向影响，随着时间推移，参数估计值不断减小，由1月期的0.0076减少至3年期(36个月)的0.0029，当观测期为36个月时，参数估计值仅在10%的水平上显著，表明这种影响呈现衰减趋势。与理论分析方向不同的是，上尾系数对个股的预期收益率产生显著为正的影响；参数估计值也随着观测期的延长表现出单调下降的特点，相对于下尾系数，其衰减速度更快；当观测期为36个月时，上尾系数对预期收益率不存在显著影响。

表7 Fama-MacBeth回归(18个月平均收益率)

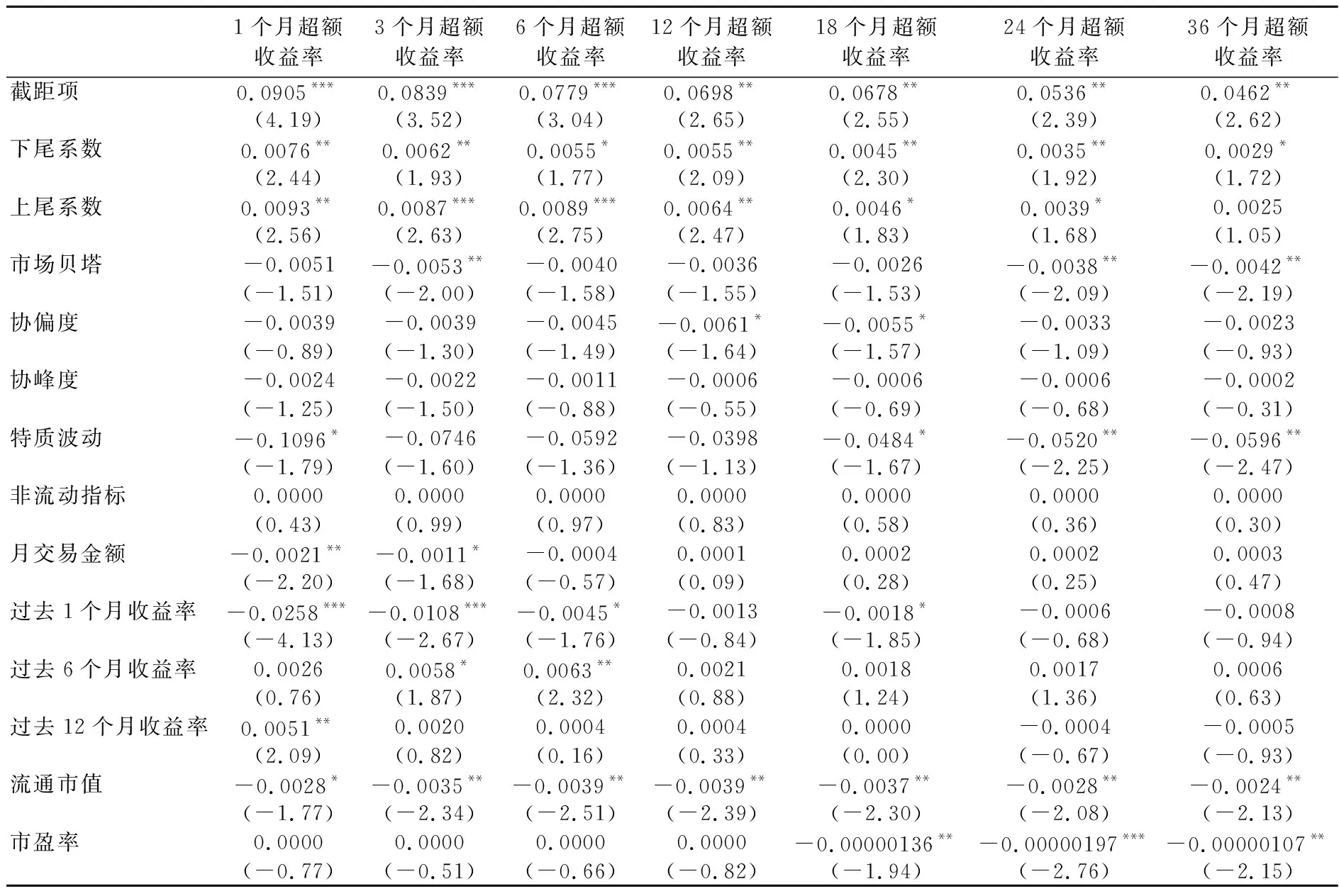
表8 不同观测期内Fama-MacBeth回归

综上，由Fama-MacBeth回归分析可知，从风险特征、交易特征、公司特征3个角度选取控制变量加入模型后，下尾系数对预期收益率具有稳健的正向影响。下尾系数对预期收益率的影响在1月期时最大，随着时间推移这种影响作用会不断减小，这说明下尾风险对个股预期收益率的冲击具有时变性，即个股的预期收益率具有时变的灾难敏感性。

四、结论与建议

本文采用二元混合Copula模型对个股的下尾风险进行估计，采用组合价差法和Fama-MacBeth回归方法分析下尾系数与个股预期收益率间的关系，检验下尾风险在个股预期收益率中是否得到合理的风险溢价，并设定7个收益率观测区间分析下尾系数对预期收益率的动态影响。实证结果发现：第一，在市场遭受极端事件冲击出现极端负收益率时，市场总体下尾系数会达到阶段性峰值，本文所估计的下尾系数能够作为下尾风险的有效衡量。第二，以下尾系数单因素分组后，高下尾系数组合的预期月收益率总是高于低下尾系数组合，下尾系数多空对冲组合收益率随着时间推移呈现倒“U”型，在观测期为18个月时达到最大。第三，在控制了上尾系数、市场风险等风险特征、历史累积收益率等交易特征及公司特征后，下尾系数与预期收益率保持稳健的正相关关系。第四，Fama-MacBeth回归结果显示，下尾系数对股票预期收益率存在显著正向影响，下尾系数参数估计值随着时间推移不断减小，对未来1个月收益率影响最大；控制下行贝塔不会影响下尾系数与预期收益率间的关系。

本文研究证实下尾系数可以较为准确地捕捉市场中的极端事件，因此，可以动态估计下尾风险，为预防市场出现崩溃灾难提供参考。尽管个股的下尾系数和上尾系数有一定的负相关关系，但是下尾风险可以一定程度解释股票的预期收益率，而上尾风险则对股票收益率影响不大，投资者更应该以下尾风险而不是上尾作为投资参考。高下尾系数的股票具有高预期回报率，所以在市场下跌之后应该选择那些对灾难敏感性大的股票。尽管结果证实下尾风险在股票预期收益率中发挥作用，下尾风险是有别于下行风险的一种非对称风险，但是这种作用随着时间推移会不断减小，因此，投资者应该注意下尾风险对个股预期收益率影响的时变性，动态管理下尾风险。