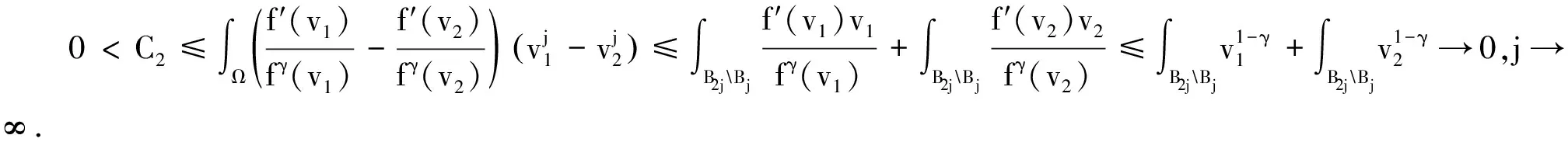一类带有奇异项的拟线性问题正解的存在性

张彩丽，梁占平

(山西大学 数学科学学院，山西 太原 030006)

考虑下面带有奇异项的拟线性方程

(1)

i∂tΨ=-ΔΨ+Ψ+η((|Ψ|2)Ψ-kΔρ(|Ψ|2)ρ′(|Ψ|2)Ψ

(2)

(3)

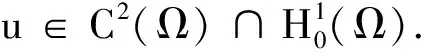
1 预备知识

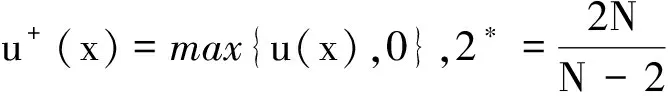
假设函数f是常微分方程初值问题

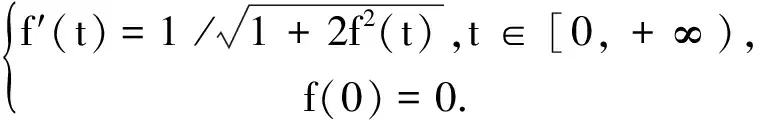
的解.令f(t)=-f(-t),t∈(-∞,0], 我们知道

引理1 函数f具有以下性质:

i)f∈C∞(R)并且是可逆的;

ii) 0≤f′(t)≤1,t∈R;

iv)f(t)/2≤tf′(t)≤f(t),t≥0;

v) |f(t)|≤|t|;

vi) (f(t))-γf′(t)关于所有的t>0是递减的.

假设v:=f-1(u), 则拟线性方程(1)的解等价于下面的半线性型方程

(4)

由于方程(1)带有奇异项u-γ, 首先考虑扰动问题

(5)

这里ε∈(0,1]. 通过利用Schauder不动点理论获得(5)的解vε, 然后通过对ε→0取极限, 得到问题(4)的解. 假设v∈L2(Ω), 由于引理(1)性质ii)知

(6)

因此可以定义映射S:L2(Ω)→L2(Ω)为

K={v(x)∈L2(Ω)|0≤v(x)≤S(0),a.e.x∈Ω}.

显然K⊂L2(Ω)是一个有界闭凸集. 假设v∈K,则

因此S(K)⊂K. 则根据Schauder不动点定理，存在vε∈K, 使得S(vε)=vε. 从而知道

(7)

又由正则性理论和极大值原理知vε>0是(5)的古典解. 另外, 有

引理2 设0<ε2<ε1≤1, 则在Ω上有vε1≤vε2.

证明令φ=vε1-vε2, 由(7)知

(8)

和

(9)

式(8)与(9)相减，有

当x∈Ω且vε1(x)-vε2(x)≤0时，有

当x∈Ω且vε1(x)-vε2(x)>0时，由f′在[0,∞)上递减知

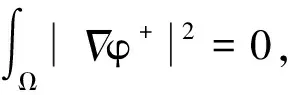
2 主要结果的证明

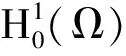
(10)

由引理2知0

在(10)两边令n→∞, 利用(10)及Lebesgue控制收敛定理知，

(11)

利用椭圆正则性理论，有v∈C2(Ω)且满足(4).

对正整数j≥1，记

(12)

由(12)左边知，存在C2>0和正整数j0,使得当j≥j0时，有

由上式，(12)及引理1 vi),iv)和v)知，当j≥j0时,

矛盾! 证毕.