一类半线性椭圆型方程组正解的存在性

郭伟香，杨燕君，张亚静

(山西大学 数学科学学院， 山西 太原 030006)

0 引言

我们研究以下半线性椭圆型方程组

(1)

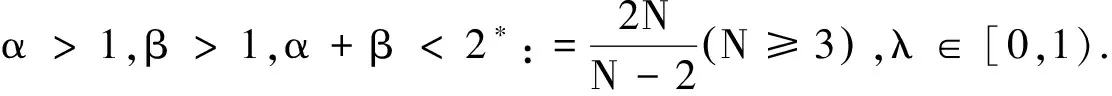
近年来，很多人研究与问题(1)相关的方程和方程组[1-3].Alves等[4]考虑了以下方程组

(2)

其中Ω∈RN(N≥3)是带有光滑边界∂Ω的有界区域,而且a,b,c∈R,α,β>1,当α+β=2*时，他们通过变分法证明了(2)正解的存在性.

Brown和Wu[5]考虑了如下有界区域上的非线性边值问题

(3)

表明在参数(λ,μ)属于R2的某个子集，f,g,h满足某些条件时,方程组(3)存在2个非负解.

张亚静[6]研究了非齐次Neumann边界问题

(4)

其中Ω∈RN(N≥5)是有界光滑区域,λ>0,μ>0为参数，α+β=2*.他证明了当f,g满足一定条件时，方程组(4)至少有2个解.

在全空间RN中Liu[7]研究了

(5)

其中α>1,β>1,α+β<2*.当a(x)，b(x)满足某些条件时，方程组(5)有无穷多个解.

在方程组(1)中当u=v，h1=h2时，为单个方程情形，Cao和Zhou[8]已经研究了

(6)

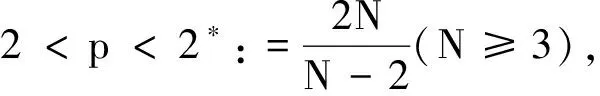
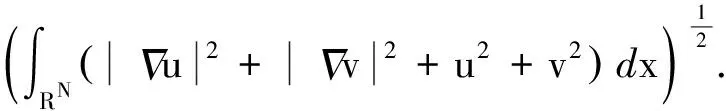
H1)

hi∈H-1(RN),hi>0,i=1,2;

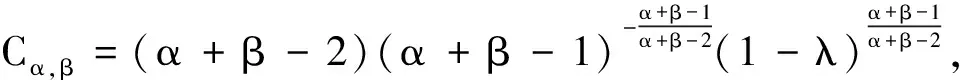
定理1 设h1,h2满足H1),H2),则问题(1)存在一个正解.

进一步考虑如下方程组:

(7)

其中F∈C1(RN)满足：

结合定理1以及上下解方法[16]证明了如下定理：

定理2 设F满足H3)，h1,h2满足H1),H2)时， 问题(7)存在一个正解.

1 Nehari流形

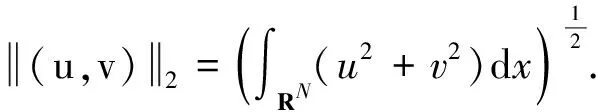
因J在H上无下界，故在Nehari流形Ν=((u,v)∈H(0,0)|〈J′(u,v),(u,v)〉=0)上考虑.

定义1Φ(u,v)=〈J′(u,v),(u,v)〉，则

则当(u,v)∈N时，Φ′(u,v),(u,v)

(8)

现在，类似Tarantello[17]将N分成如下3个部分:

Ν+={(u,v)∈Ν|〈Φ′(u,v),(u,v)〉>0}，

Ν0={(u,v)∈Ν|〈Φ′(u,v),(u,v)〉=0}，

Ν-={(u,v)∈Ν|〈Φ′(u,v),(u,v)〉<0}.

为了证明定理1和定理2，先给出以下基本结论.

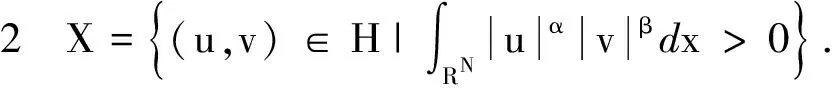
引理1 设h1,h2满足H1),H2)，则对于每一个(u,v)∈X，有

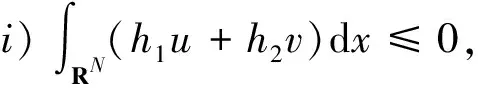
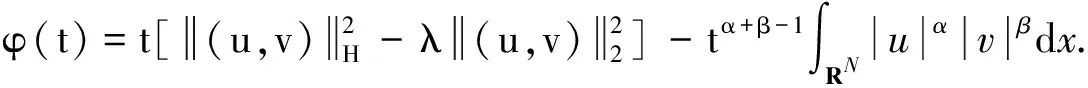
(9)

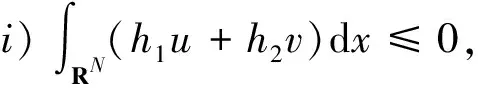
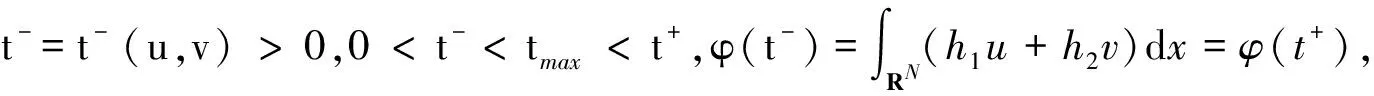
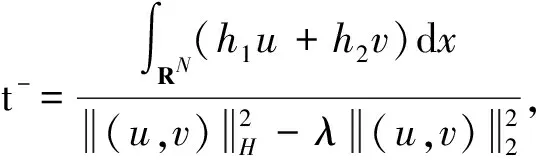
引理2 设h1,h2满足H1),H2)，有Ν0=0/.

证明用反证法.设Ν0≠0/，即存在(u,v)∈Ν0.下面分2种情况讨论：

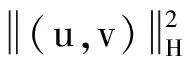
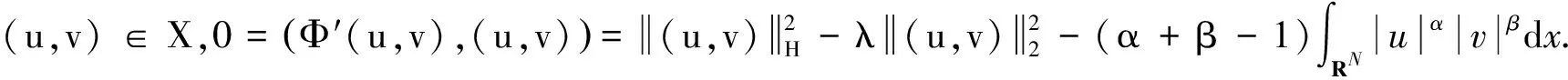
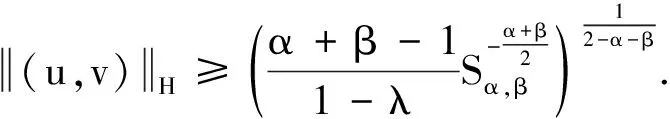
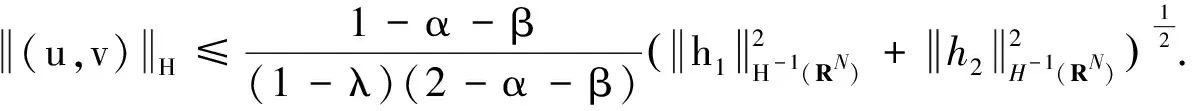
与假设H2)矛盾.综上所述，可得Ν0=0/.

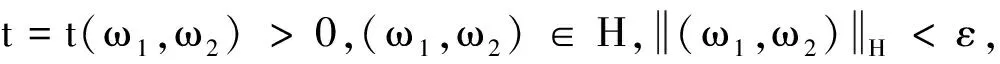
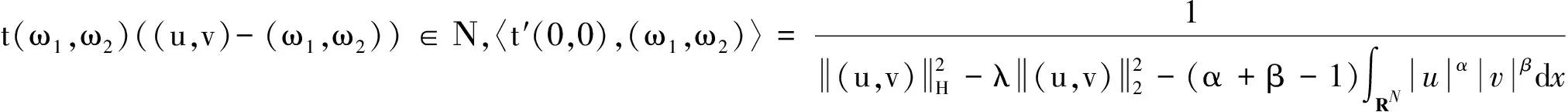
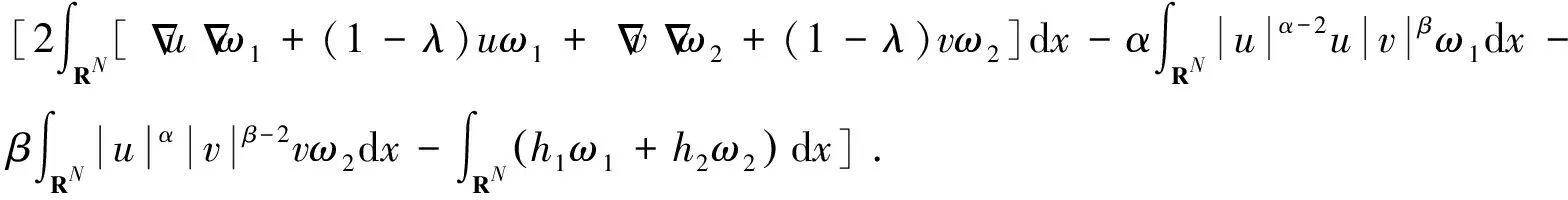
(10)

证明定义F:R×H→R，

因为F(1,(0,0))=0，Ft(1,(0,0))≠0，在点(1,(0,0))处应用隐函数定理即证.

2 定理证明

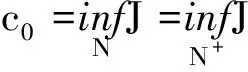
证明首先，我们证明J在N上有下界.事实上，对于(u,v)∈Ν，有

则

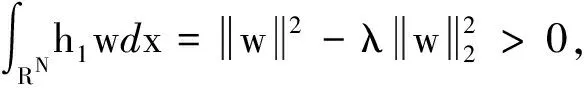
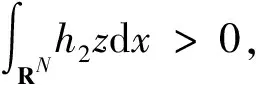
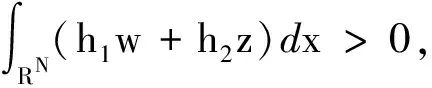
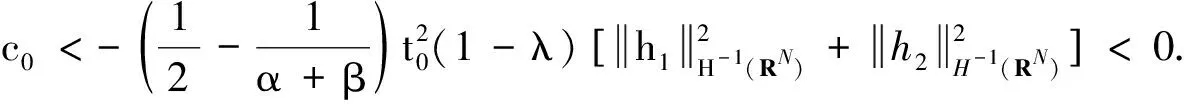
由Ekeland变分原理[19],J(u,v)在N中存在极小化序列{(un,vn)}满足

(11)

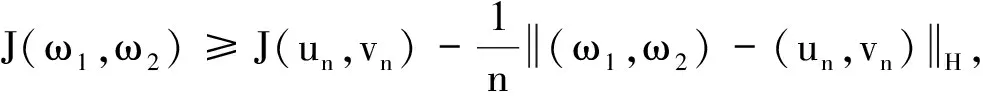
(12)

则当n充分大时,由(11)式可得

(13)

则有

(14)

因此,对n充分大时,有un≠0或vn≠0.

由(13)和(14)式,可得

(15)

(16)

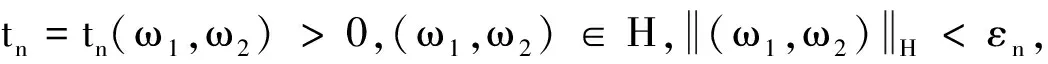
则从(12)式可得

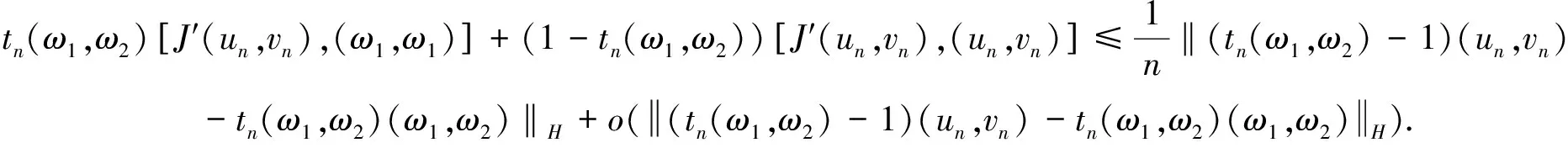
由εn的选择，以及(15)式, 可得

(17)

若证明了

(18)

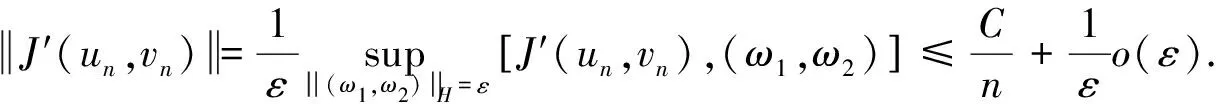
其中C>0与ε和n无关.取ε→0，则可得(16)式.

现在证明(18)式.事实上,由(10)式

由(15)式可知,要证明(18)式,只需证明对某个δ>0,对n充分大时，有

用反证法:设存在{(un,vn)}的一个子序列(仍记为{(un,vn)}),有

(19)

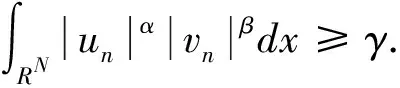
由(un,vn)∈Ν，对n充分大时,可得

(20)

由H1),H2)可知，存在ε0>0，使得对n充分大时，

这与(20)式矛盾.因此,证明了(18)式.

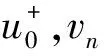
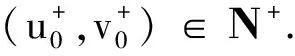
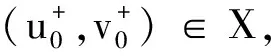
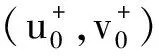
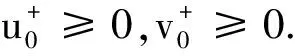
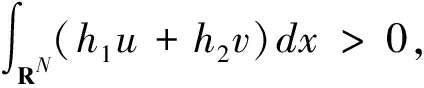
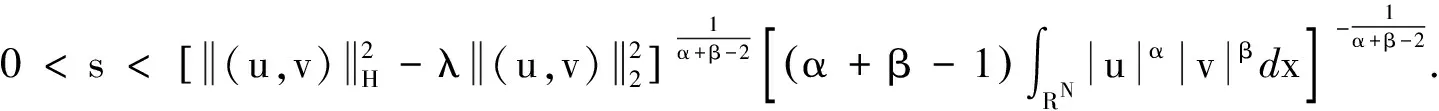
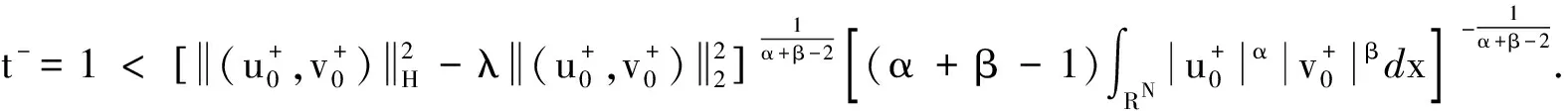
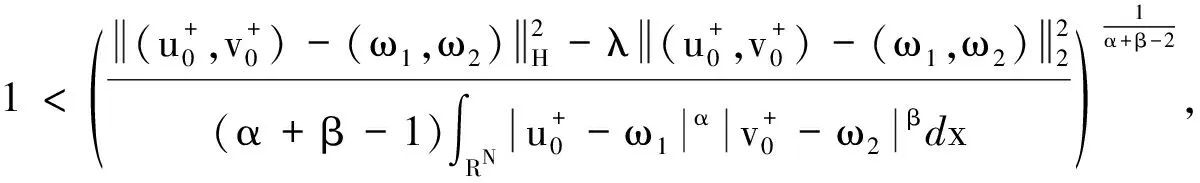
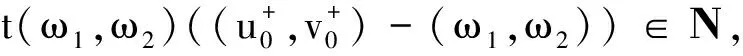
由t(ω1,ω2)的连续性,以及t(0,0)=1，可以假设

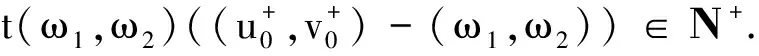
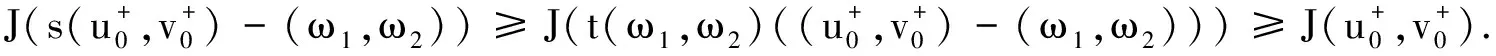
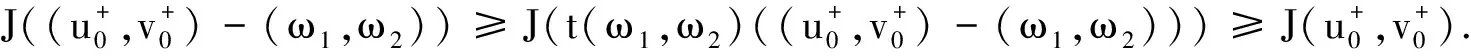
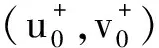
证明定理1 由命题1,立即可以得到定理1的证明.