基于区域划分的交直流混联配电网潮流计算方法

张 璐，丛鹏伟，许 彪，余顺江，李欢林

(1.电力系统及发电设备控制和仿真国家重点实验室(清华大学)，北京 海淀 100084；2.东南大学电气工程学院，江苏 南京 210096； 3.中国农业大学信息与电气工程学院，北京 海淀100083)

0 引言

随着柔性直流技术的不断成熟，基于电压源换流器(voltage source converter,VSC)的交直流混合配电网成为未来城市配电网的发展趋势。

目前，交直流混合配电网潮流计算方法主要分为统一迭代法和交替迭代法两种。统一迭代法将交流系统方程和直流系统方程联立，对交流系统变量和直流系统变量统一进行迭代求解，完整地考虑了交、直流系统间的耦合关系。统一迭代法具有良好的收敛性，但难以处理交直流系统灵活运行方式和复杂的控制策略。交替迭代法则是在迭代计算过程中将交流系统方程和直流系统方程分别进行迭代求解，易于处理复杂的控制策略，并能够利用现有交流潮流计算方法，便于实现与应用[1]。

文献[2-3]采用了统一求解思想，其中文献[2]提出了一种增广直角坐标下的交直流潮流计算方法，使得该方法可以适应于多种拓扑形式的交直流混合配电网潮流计算。文献[3]仅以交流直流系统节点电压作为最小状态变量集合，简化了求解的复杂度，但该文章的假设忽略了换流站运行损耗，计算结果不准确。此外，当面对复杂网络计算时，雅各比矩阵的形成与计算会变得十分困难。

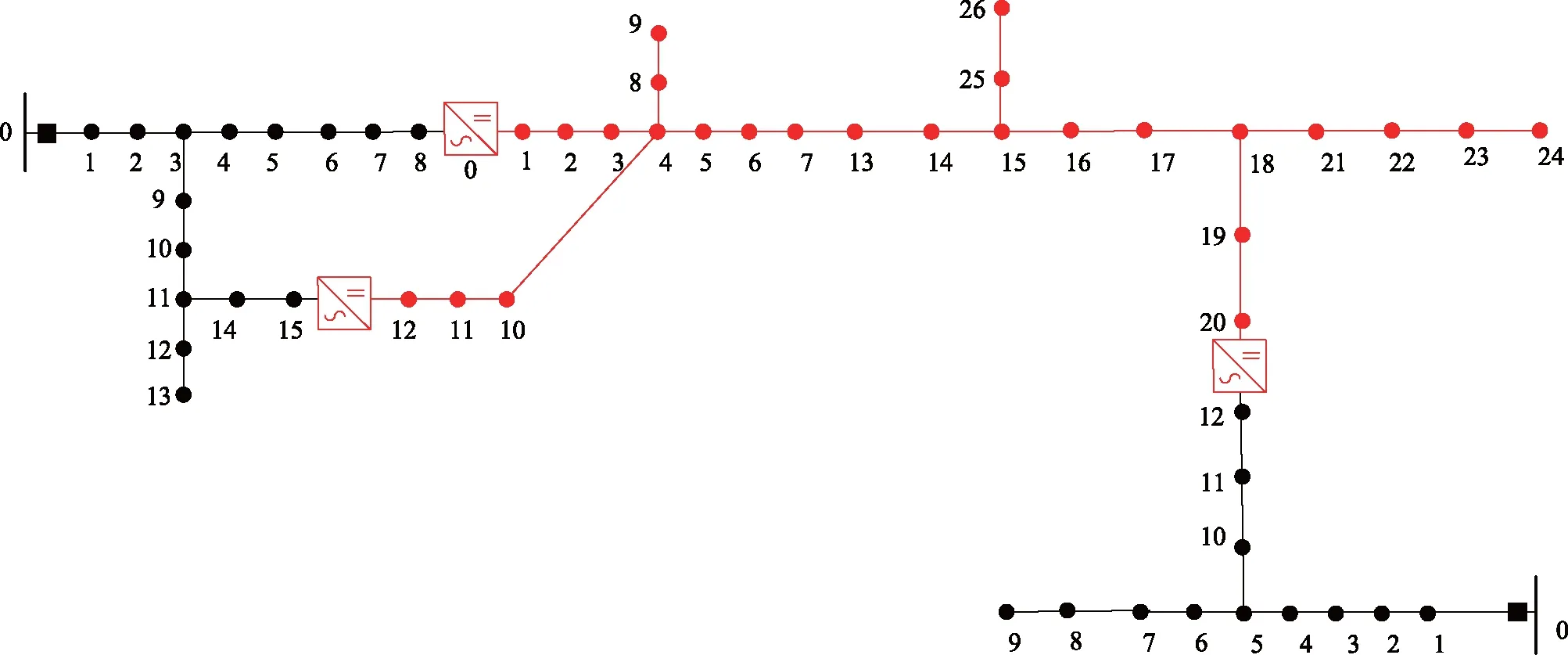
图1 交直流混合配电网Fig.1 Hybrid AC/DC distribution network

文献[4-5]采用了交替迭代思想，其中文献[4]提出了一种通用交直流网络潮流交替迭代方法，该算法根据VSC换流站的不同控制方式在交流侧和直流侧解耦等效，先进行直流电网潮流迭代，后进行交流电网潮流迭代，二者交替计算直至直流电网、换流站和交流电网全部收敛。文献[5]提出了一种可适用于含有环网的多端直流配电网潮流计算方法，通过控制直流系统有功功率，直流系统潮流只需计算一次，避免交流系统与直流系统间多次进行交替迭代；采用节点关联矩阵对网络结构进行自动搜索和自动开环处理，提出了针对环网和下垂节点的统一功率修正方法。然而，基于交替迭代思想的潮流计算方法可能无法保证算法收敛性。

本文提出了一种针对含多端直流配电网的交直流混合配电网潮流计算方法，基于PQ、VQ两种电压源换流器控制方式，首先采用定直流电压方式计算直流系统潮流，然后根据直流潮流计算结果，将所有换流器节点等效为PQ节点，计算交流系统潮流，实现了交、直流系统的解耦计算，降低了计算复杂度；同时，通过适当简化换流器运行损耗计算模型，在丧失一定计算精度的前提下，潮流计算可以避免交、直流系统间的交替迭代计算，保证算法收敛性，使运算效率得到提升。

1 交直流混合配电网基本结构

图1显示了通过直流改造形成的交直流混合配电网的基本结构。通过网络拓扑分析可将图示交直流混合配电网划分为若干个交流子系统和直流子系统，图中共有1个直流子系统和2个交流子系统，不同类型子系统之间通过换流器相连。

1.1 换流器结构

换流器能够实现直流电与交流电间的相互转换，在交直流混合配电网中是极其重要的设备。传统直流输电技术采用基于大功率晶闸管的电流源型换流器，存在潮流控制不灵活、逆变器交流侧需要无功电源支撑、容易换相失败、需配置大容量滤波与无功补偿装置的缺点，因此电流源型换流器并不适合应用在交直流混合配电网中[6]。

1.1.1 不同类型换流器对比

目前柔性直流技术主要采用VSC和模块化多电平换流器(modular multilevel converter, MMC)，根据其具体结构的不同又可以分为两电平VSC、三电平VSC、半桥MMC、全桥MMC以及双钳位型子模块。各种换流器基本结构与特性对比见表1。

综合考虑运行可靠性、控制灵活性等方面，在交直流混合配电网中应采用VSC[7]。

1.1.2 基于换流器单极对称结构接线的直流线路最大传输容量

图2所示为电压源换流器对称结构的接线方式，该种接线方式将三相线路分别用作直流正极线、直流负极线和金属回路线。

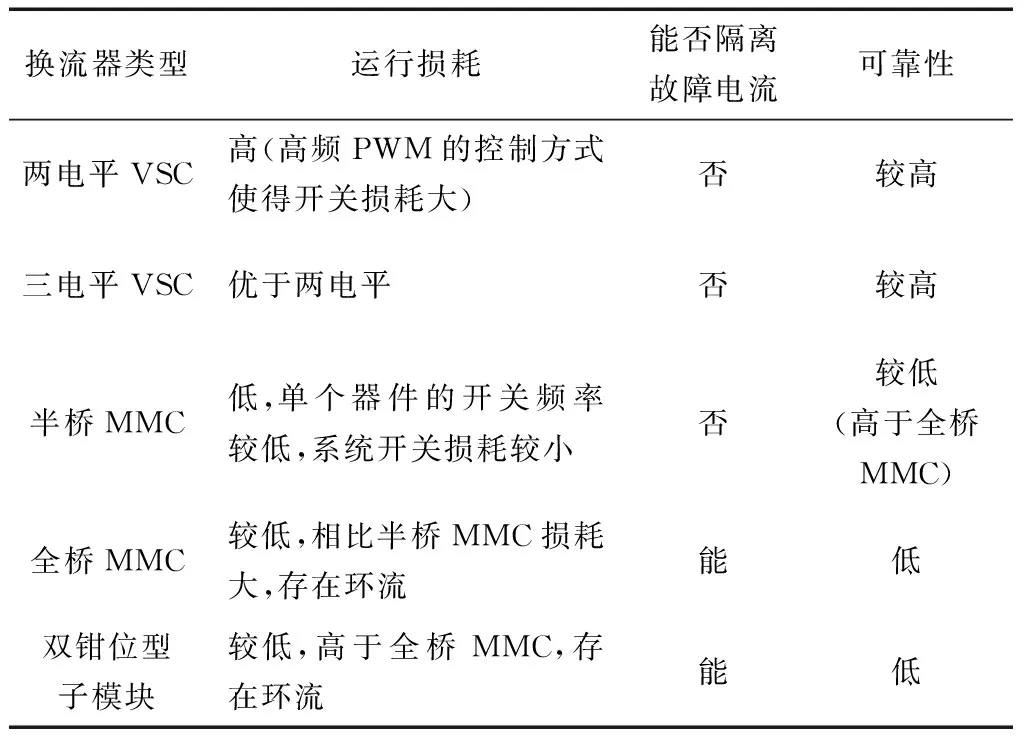
表1 换流器基本结构及特性对比Table 1 Basic structure of converter and characteristic contrast

图2 换流器对称结构接线Fig.2 Symmetrical structure of converter connection

特别的，当双回交流线路被改造为直流线路时，可以采用换流器无金属回路线的对称结构接线方式，这样就可以使两回交流线路转为三回直流线路运行，但必须要保证每一回线路的负荷分布均衡。图3所示为直流运行状态下电缆线和架空线的不含中性线对称结构。

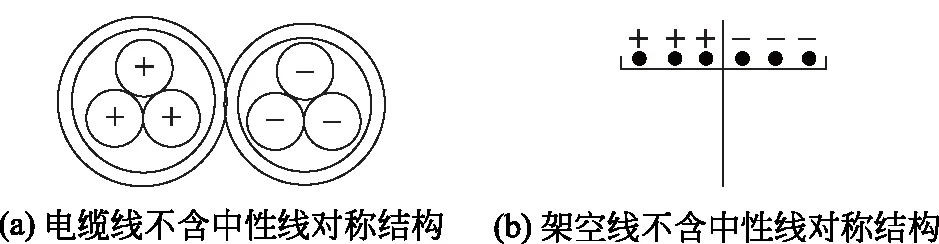
图3 电缆线和架空线的不含中性线对称结构Fig.3 Symmetrical structure of cable and overhead line without neutral line

直流改造前，双回交流线路的最大传输容量可表示为

(1)

当采用换流器无金属回路线的对称结构接线方式，将原双回交流线路改造为三回直流线路时，线路的最大传输容量可表示为

Pmax_DC=6UDCIDC

(2)

为了定量计算改造后传输容量的提升效果，定义：

(3)

通过计算可以得到，σ的值可达1.587[8]，最大传输容量提升了超过50%。

1.2 换流器控制方式

换流器可以从有功功率、无功功率、交流电压、直流电压等变量中选择其中两个变量进行控制[9]。根据控制状态量的不同，可以分类为UDC-θ控制，UDC-Q控制，UDC-UAC控制，P-Q控制等[10]。根据采用控制方式的不同，本文所讨论的交直流混合配电网包含两种类型的VSC，分别称为VSC1、VSC2。

(1) VSC1。采用V-Q控制方式，该类型对换流器直流侧电压和注入交流系统的无功功率进行控制。对于直流系统来说，换流器相当于一个恒定直流电压源；对于交流系统来说，换流器仍可以等效为一个恒功率型交流负荷[11]。

(2) VSC2。采用P-Q控制方式，该类型对换流器注入交流系统的有功和无功功率进行控制。对于交流系统和直流系统来说，换流器都相当于一个恒功率型负荷。

图4所示为不同控制方式VSC的配置结果，对于图中的多端直流子系统，其中一个VSC采用V-Q控制方式，其余VSC采用P-Q控制方式。

1.3 换流器运行损耗模型

本文在计算换流器运行损耗时采用了广义换流器损耗模型，该损耗模型是由ABB公司基于一个容量为600 MVA，电压等级为±300 kV的VSC-HVDC系统研究得到的[12]，该损耗模型可表达为：

(4)

式中：Ic为VSC交流侧流过的电流；Pc和Qc分别为VSC在交流侧交换的有功功率和无功功率；Uc为VSC交流侧电压；A为VSC-HVDC系统中VSC的空载损耗实测值；B为VSC-HVDC系统中VSC关于Ic的线性损耗系数；C为VSC-HVDC系统中VSC关于Ic的非线性损耗系数。

损耗系数A、B、C的计算公式[13]如下：

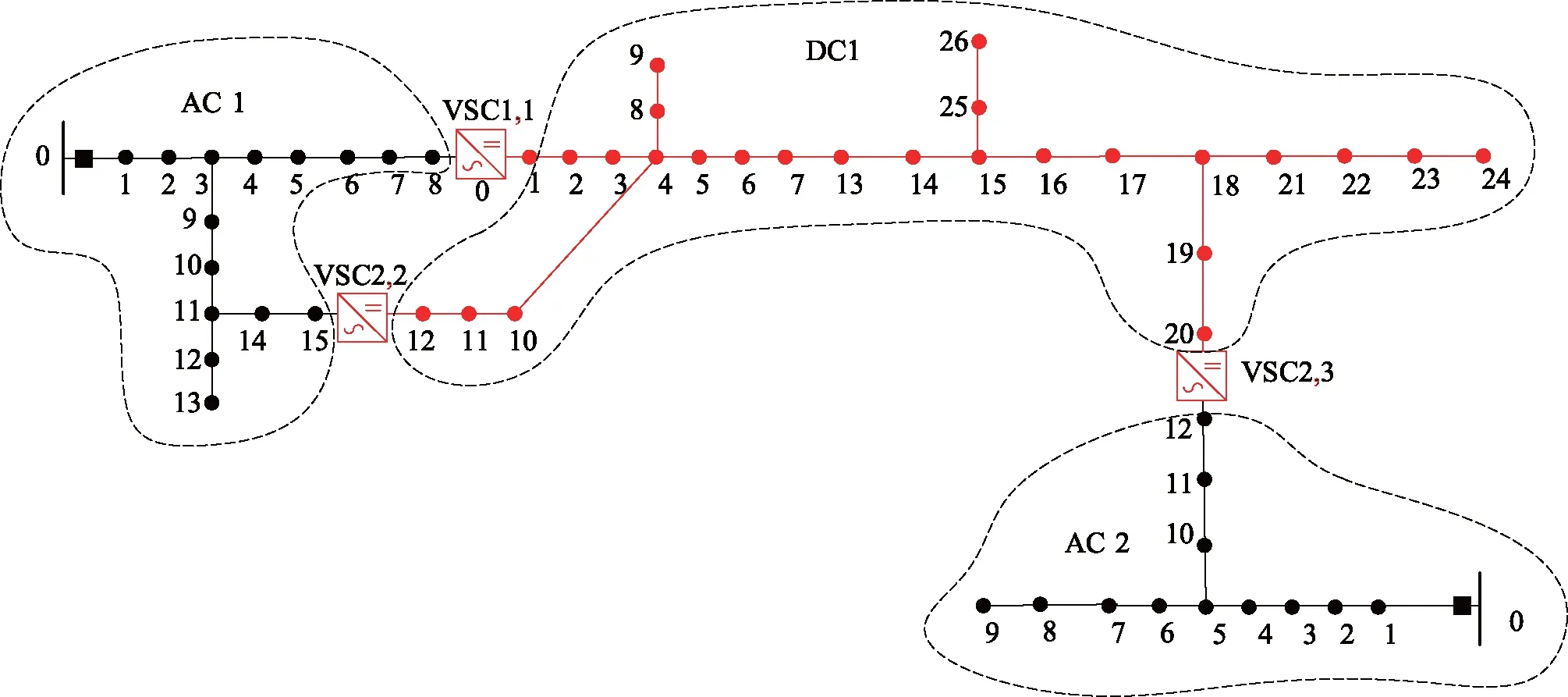
图4 两种类型VSC配置示意图Fig.4 Configurations of two types of VSCs

(5)

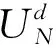
目前已有文献[13，2]将该换流器损耗模型应用于中压配电网中，综上所述在交直流混合中压配电网中VSC的运行损耗可以表示为：

其中VSC运行损耗计算采用广义换流器损耗计算模型：

(6)

2 交直流混合配电网潮流计算

在进行交直流混合配电网的潮流计算时，对于直流子系统而言，可将采用V-Q控制方式的VSC1等效为一个恒定直流电压源，将采用P-Q控制方式的VSC2等效为一个恒功率型直流负荷；对于交流子系统而言，可将采用V-Q控制方式的VSC1、采用P-Q控制方式的VSC2均等效为一个恒功率型交流负荷。通过这种方式，可以实现交直流系统的解耦，即交流潮流和直流潮流的分开求解。图5所示为交直流混合配电网潮流求解算法流程图，具体步骤如下。

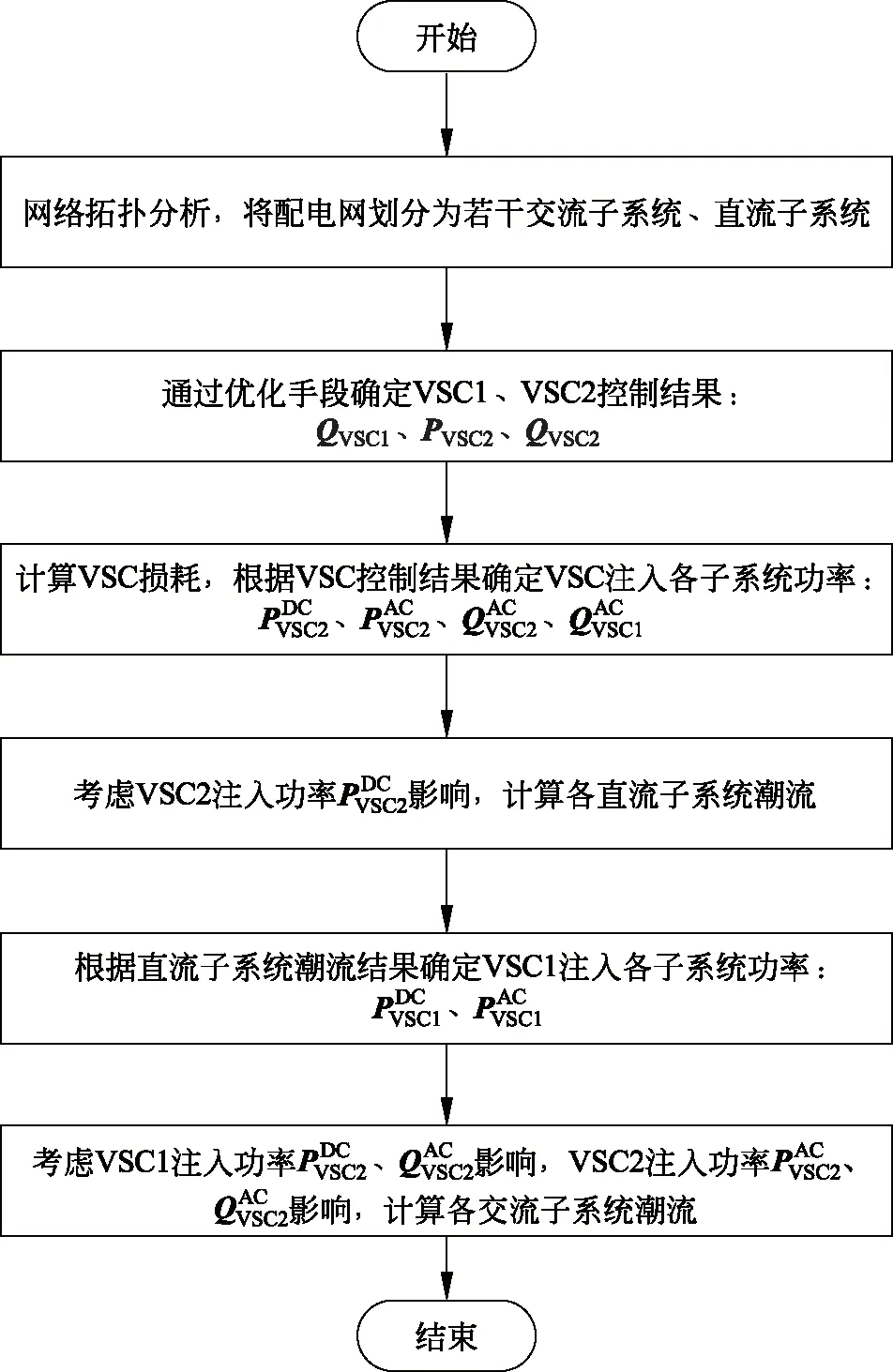
图5 交直流混合配电网潮流求解算法流程图Fig.5 Flow chart of power flow algorithm forhybrid AC/DC distribution network

(1) 网络拓扑分析，将整个配电网分为若干个交流子系统、直流子系统。

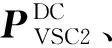
式中：PVSC2,i>0表示VSC2工作在整流状态，PVSC2,i<0表示VSC2工作在逆变状态。

(3) 对于各直流子系统，在VSC1位置处设置虚拟节点，并将其定为平衡节点(该节点电压值为直流系统额定电压值Udc)。对与VSC2紧邻的节点施加来自于VSC2的注入有功功率，则该节点的功率平衡方程可表示为

(11)

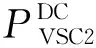
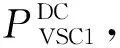
(12)

(5) 对于各交流子系统，对与VSC紧邻的节点施加来自于VSC的注入功率，则该节点的功率平衡方程可表示为：

(13)

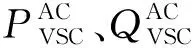
3 仿真算例

3.1 算例介绍

仿真时采用的交直流混合配电网拓扑结构见图4，该配电网共包含56个节点，1个直流子系统和2个交流子系统，总有功负荷大小为12 MW；其中，直流子系统采用三回线路，交流子系统采用两回线路[14]；直流子系统电压等级为16 kV[15]，交流子系统电压等级为10 kV；VSC1(1)控制无功功率为1 MW，VSC2(2)和VSC2(3)控制有功、无功功率均为1 MW。

3.2 仿真模型

为验证本文所提交直流混合配电网潮流计算方法的正确性，本文还采用商业化潮流求解软件DIgSILENT对56节点交直流混合配电网进行了潮流求解。

利用DIgSILENT软件进行潮流计算时，直流线路各节点负荷采用三回线路供电，交流线路各节点负荷采用两回线路供电，模型中网络拓扑与图4所示56节点交直流混合配电网拓扑完全吻合。

仿真中主要参数的配置结果如表2所示。

表2 参数设置Table 2 Parameter settings

3.3 仿真结果

分别采用本文所提方法及商业化潮流求解软件DIgSILENT对56节点交直流混合配电网进行潮流求解。两种方法的计算结果如表3—5所示。

利用平均相对误差(mean absolute percentage error, MAPE)衡量本文所提交直流混合配电网潮流计算方法的精确度。分别针对交直流混合配电网的节点电压和支路功率，计算本文所提方法与商业软件DIgSILENT计算出的潮流结果之间的平均相对误差，结果如表6所示。

结果表明，两种方法计算出的潮流结果差距很小，从而验证了本文所提交直流混合配电网潮流计算方法的正确性。

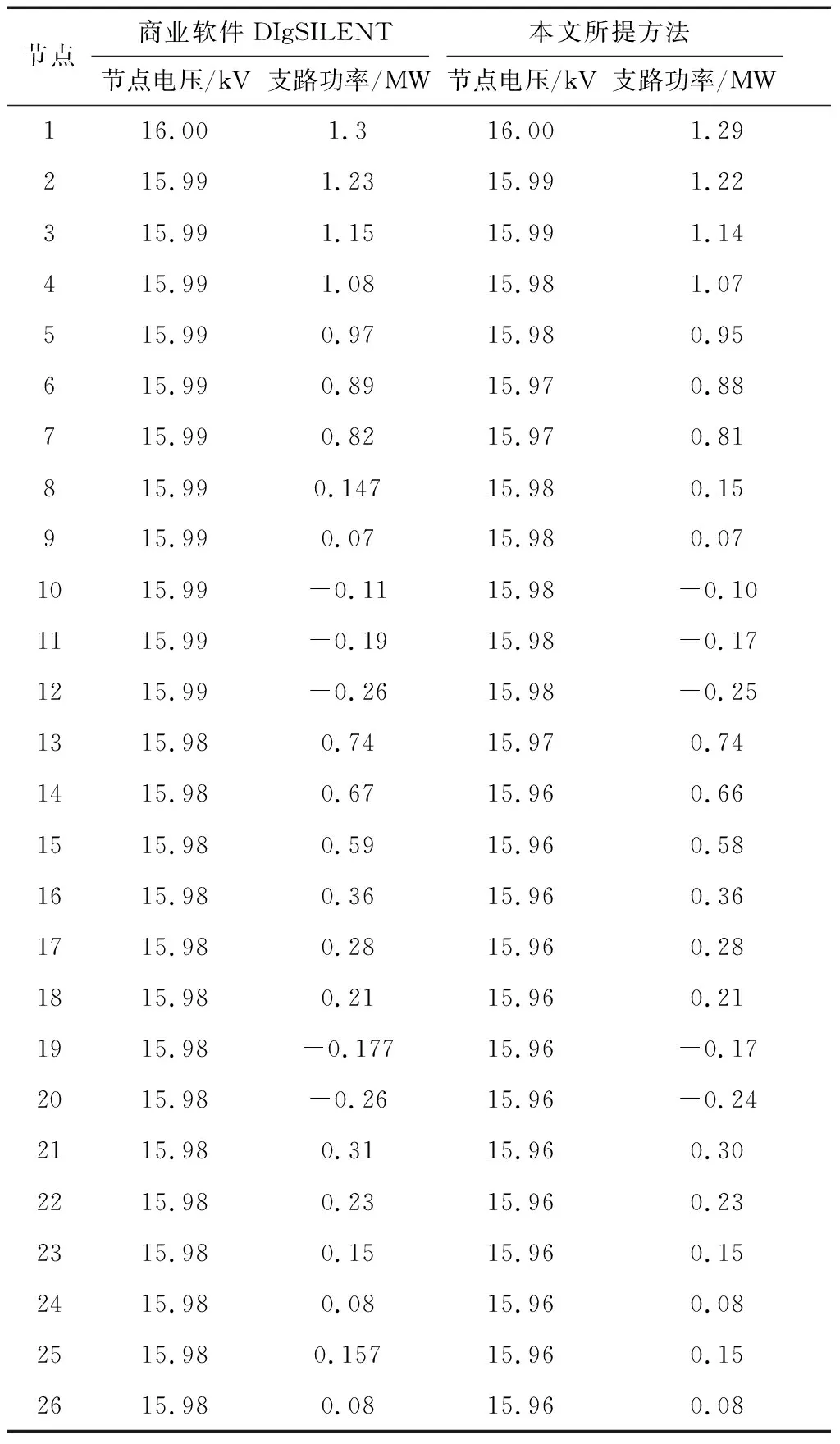
表3 56节点交直流混合配电网潮流计算结果-DC1直流子系统Table 3 Calculation results of AC/DC power flow in 56 nodes-DC1 DC subsystem

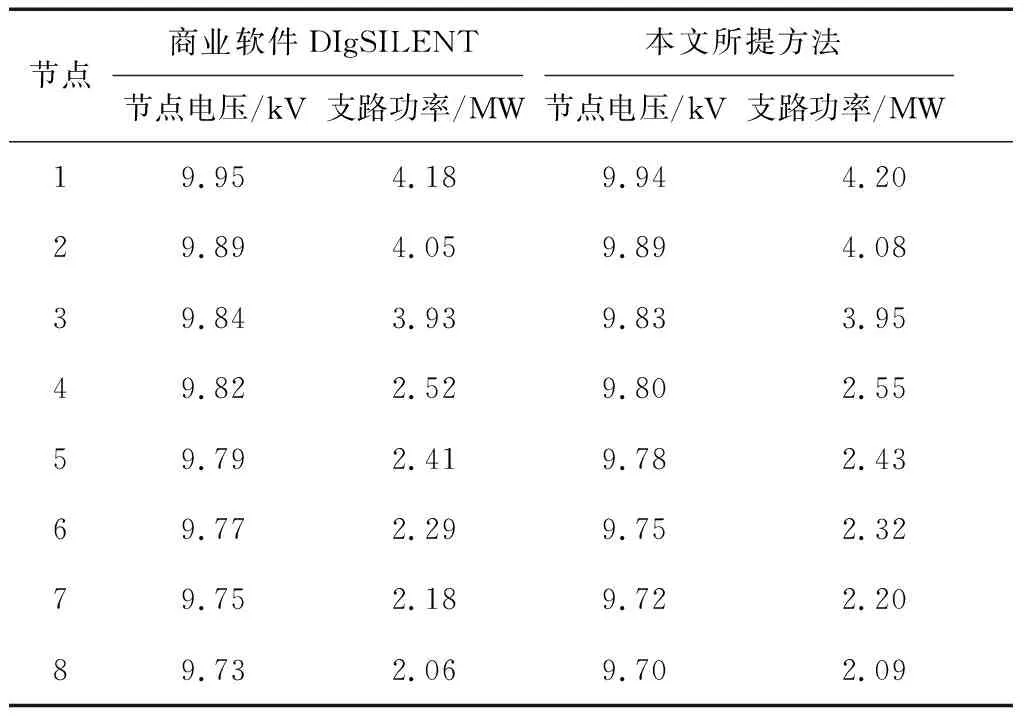
表4 56节点交直流混合配电网潮流计算结果-AC1交流子系统Table 4 Calculation results of AC/DC power flow in 56 nodes-AC1 AC subsystem

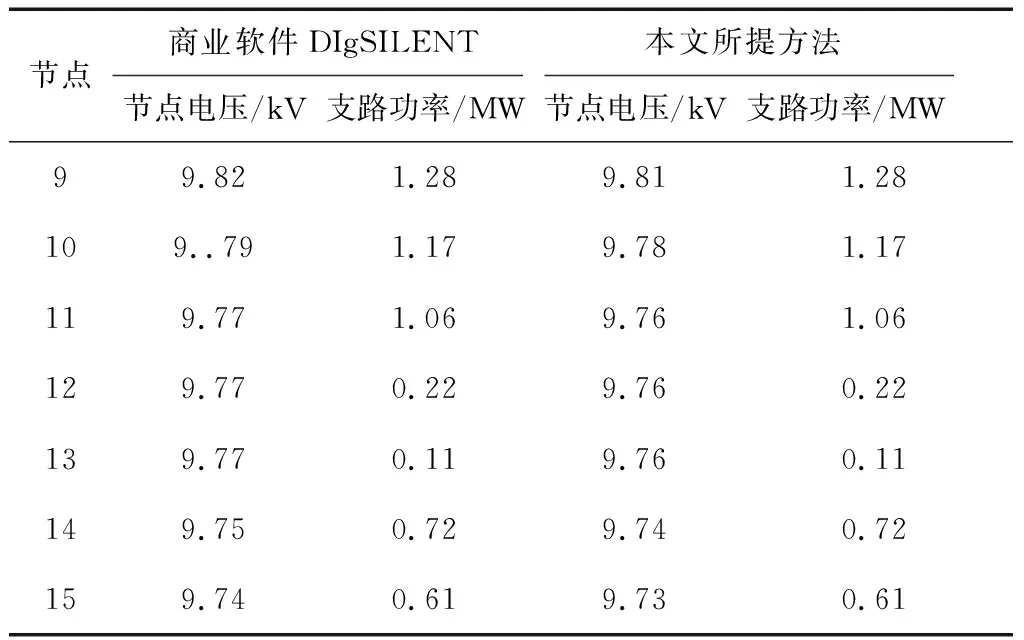
续表

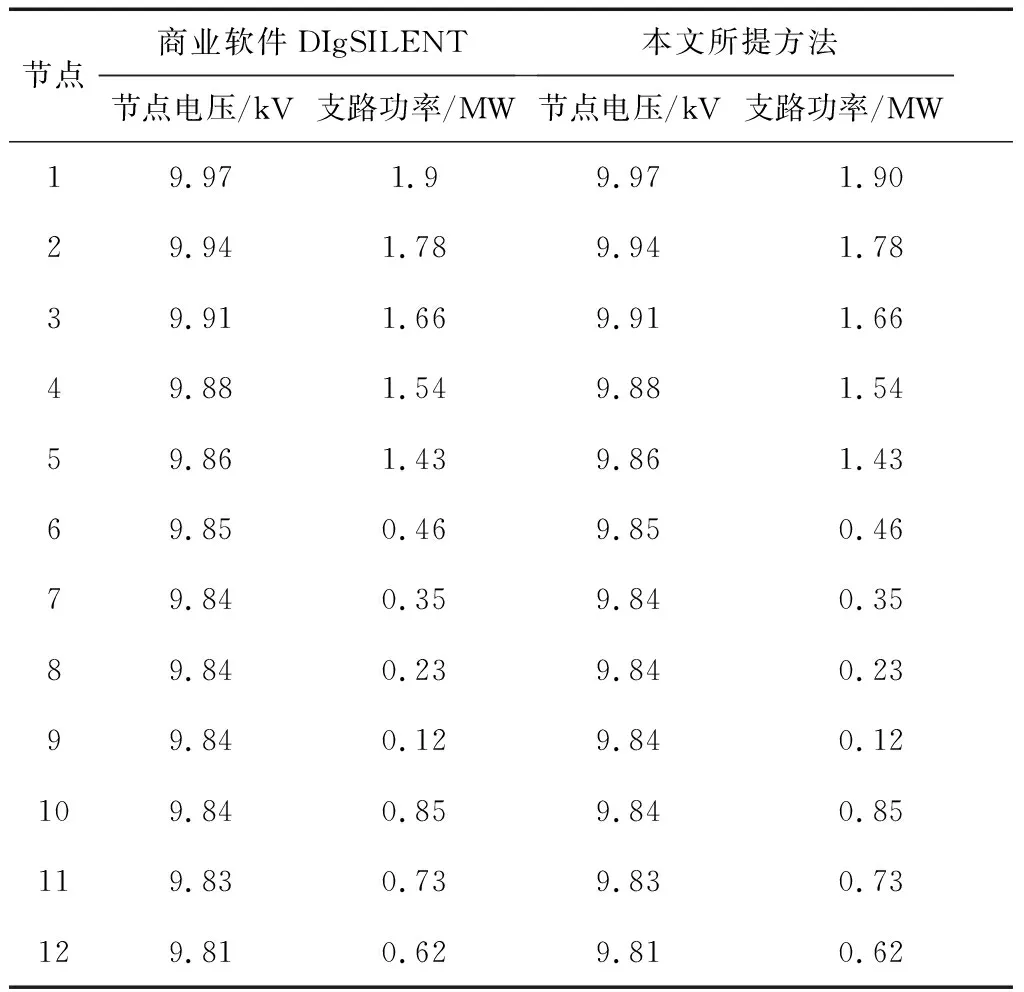
表5 56节点交直流混合配电网潮流计算结果-AC2交流子系统Table 5 Calculation results of AC/DC power flow in 56 nodes-AC2 AC subsystem

表6 潮流计算结果的平均相对误差Table 7 Average relative error of power flow calculation results

4 结论

本文研究了交直流混联配电网潮流计算方法，提出了基于区域划分的计算思路。通过对不同类型换流器进行对比分析，证明了电压源换流器在运行可靠性及控制灵活性方面具有更大优势。采用了基于VSC单极对称结构的接线方式，将双回交流线路改造为三回直流线路可使线路最大传输容量提升超过50%。

本文所提交直流潮流计算方法可适用于含多端直流的复杂交直流混合配电网，利用不同控制方式下VSC在交、直流侧的解耦等效，实现了交、直流系统解耦计算，降低了计算复杂度。

通过适当简化换流器运行损耗计算模型，在丧失一定计算精度的前提下，潮流计算可以避免交、直流系统间的交替迭代计算，保证算法收敛性，使运算效率得到提升。