基于小波分解的超短期风速混合模型组合预测

郑若楠

(中国大唐集团有限公司科技与信息化部，北京 西城 100033)

0 引言

随着化石能源的日益减少与环境污染的日益严重，各国均对可再生能源进行了大力发展。根据风电发展“十三五”规划，2020年底中国风电累计并网装机容量将达到2.1亿 kW以上，风电年发电量4 200亿 kW·h，约占总发电量的6%[1]。随着风电并网规模的快速扩大，风电的不确定性对电网调度、电力系统安全稳定运行及电能质量的影响日益彰显[2]，也对风电功率的超短期预测精度提出了更高的要求[3]。而风速与风电功率间的三次方关系，使其成为影响风电功率的最主要因素。准确的超短期风速预测，是解决风力发电并网基本问题的有效途径，有利于电力部门及时调整调度计划，减少电力系统运行成本，降低风电对电网的不利影响，提高风电的并网比例[4]。

超短期风速预测通常是指未来0～4 h的风速预测，时间分辨率不超过1 h，所得结果将直接应用于电力系统的实时调度。目前，国内外基于时间序列的超短期风速预测方法大体可分为：1)基于原始风速序列的直接预测方法。直接对实测风速序列进行建模预测，常用方法包括持续法[5]、自回归差分移动平均模型[6]、卡尔曼滤波[7]、神经网络[8-9]、支持向量机[10]、相关向量机[11]以及各模型的组合方法[12-13]等。2)基于风速分解后各频率序列的间接预测方法。风速时间序列可以看作是由不同频率分量叠加而成，故可采用分解-合成方法对其进行超短期预测[14]，即先对实测风速序列进行分解得到各频率序列，而后应用上面所提及的超短期风速直接预测的某一常用方法对各频率序列进行建模预测，再对各频率序列所得预测结果进行合成，最终得到超短期风速预测结果。目前，对风速时间序列进行分解的常用方法包括小波分解[15]、经验模态分解[16]、变分模态分解[17]等。与基于原始风速序列的直接预测方法相比，采用基于风速分解后各频率序列的间接预测方法进行超短期风速预测时，由于对各频率序列分别进行建模预测可使预测精度在一定程度上有所提高。

针对超短期风速的间接预测方法在各频率序列均采用同一模型进行预测，即单一模型组合预测方法，仅模型参数发生变化，并未从根本上考虑各频率序列间的差异性和可预测性，无法充分依据各频率序列特点进行高精度预测。针对上述问题，本文中提出一种基于小波分解的超短期风速混合模型组合预测方法，针对小波分解后所得到的各频率序列特点，选取合适的方法并建立相应的模型对其进行预测，进而提高超短期风速预测精度。

1 研究思路与基本预测模型

1.1 研究思路

风速时间序列可看作是由多种频率序列组合而成，通过小波分解可以很好地提取各频率序列的隐藏特征，但由于各频率系列的特性不同导致其可预测性存在差异，针对各频率序列特点选取合适的方法进行预测可提高预测精度。目前所采用的超短期风速预测方法中，无论是直接预测法还是间接预测法，均未从根本上考虑各频率序列间的差异。为提高超短期风速预测精度，本文中提出了一种基于小波分解算法的超短期风速混合模型组合预测方法，可依据各频率序列特点选取合适的方法模型进行预测。本文中所采用的的基本预测模型分别为自回归差分移动平均模型(autoregressive integrated moving average model, ARIMA)，反向神经网络(back propagation neural network, BPNN)与支持向量机(support vector machine，SVM)。

1.2 小波分解与重构模型

小波分解[15]是处理多频率分量组成的时间序列的一种有效手段，如风速时间序列，其实质是将原始信号f(x)从j+1尺度到j尺度的逐步分解过程，即对信号从高分辨率到低分辨率的分解过程，最终将一组含有综合信息的原始序列信号分解为J+1组具有不同特征的序列信号，包括DJ-1，DJ-2，…，D0，A0，其中0≤j≤J-1。分解过程为

式中:hk-2n与gk-2n分别为正交小波的传递系数；Aj表示近似信号，可反映该序列的整体变化趋势；Dj表示细节信号，可反映蕴含在原始序列中不同频域的随机扰动；k表示整节点标记的时移离散。

小波重构算法是小波分解算法的逆过程，对于超短期风速预测而言，若想得到最终预测结果，需要将各频率序列的预测结果进行重构。重构过程为

(3)

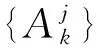
小波分解与重构的具体流程如图1所示。

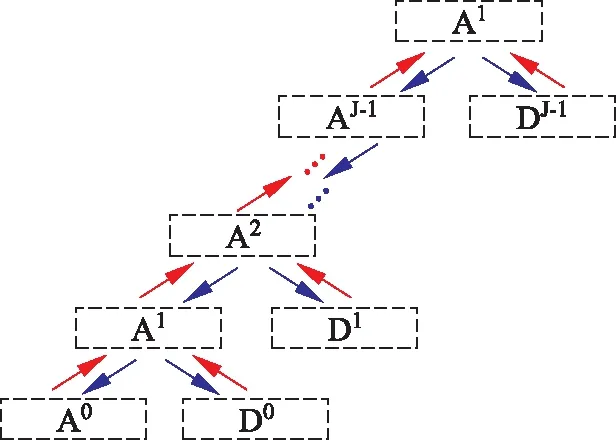
图1 小波分解与重构过程示意图Fig.1 Process of wavelet decomposition and reconstruction

1.3 基本预测模型

本部分对ARIMA、BPNN与SVM三种基本预测模型，包括的建模原理进行简单介绍，并描述了其应用于超短期风速预测时的建模过程。

1.3.1 ARIMA

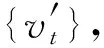
(4)

式中：p，q分别为自回归模型与移动平均模型的阶数；βi,αi分别为自回归模型与移动平均模型的各项系数；εt为随机误差项。

1.3.2 BPNN

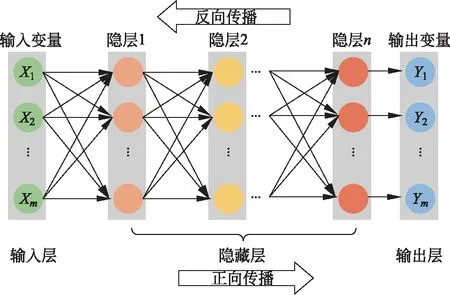
图2 BPNN拓扑结构图Fig.2 Topology of BPNN

BPNN是一种多层前馈神经网络，是目前应用最广泛的神经网络模型之一，属于有导师学习[8]，其拓扑结构如图2所示，包括输入层、隐藏层与输出层。应用BPNN进行超短期风速预测时，其网络的信号传送由两部分组成，即正向传播与反向传播。正向传播中，学习样本作为输入进入输入层，经过隐含层运算后传至输出层，每层神经元状态只影响下层神经元状态，若输出层未得到期望的输出结果，则计算误差变化值，而后进入误差反向传播，并逐层调整权值，使误差达到最小。最终以误差结果为依据，确定误差最小时的网络模型进行风速预测。

1.3.3 SVM

SVM是一种基于统计学理论的新型机器学习算法，近年来广泛应用于统计分类与回归分析中[10]。该算法不仅具有处理非线性回归问题的能力，并且在计算过程中可获得全局最优解，适用于小样本、非线性和高维的模式识别问题。将其应用于超短期风速预测时，首先需采用非线性映射函数将原始样本在低维空间中的非线性关系映射到高维空间中，使其变为线性关系再进行求解，映射后高维空间的线性回归函数为

f(x)=〈wφ(x)〉+b

(5)

式中：w为权向量；φ(x)为非线性映射函数；b为阈值。

此时可将回归问题转化为如何寻找权向量w和阈值b的最优解，如式(6)所示。

(6)

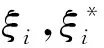
而式(6)中最小值的表达式可转换为拉格朗日函数的对偶形式，超短期风速预测模型如式(7)所示。

(7)

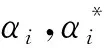
2 超短期风速混合模型组合预测方法

2.1 建模流程

风速时间序列可看做由不同频率分量叠加而成，因此可考虑将其分解，对各频率序列进行预测后再对其合成，以得到最终预测结果。传统超短期风速预测方法中，无论是直接预测法还是间接预测法，均未从根本上考虑各频率序列间的差异性，所得结果往往精确度不高。因此本文中提出了基于小波分解算法的超短期风速混合模型组合预测方法，可根据各频率序列特点选择不同方法模型分别对其进行预测，进而在一定程度上提高预测精度。所提方法建模流程如图3所示，具体过程如下。

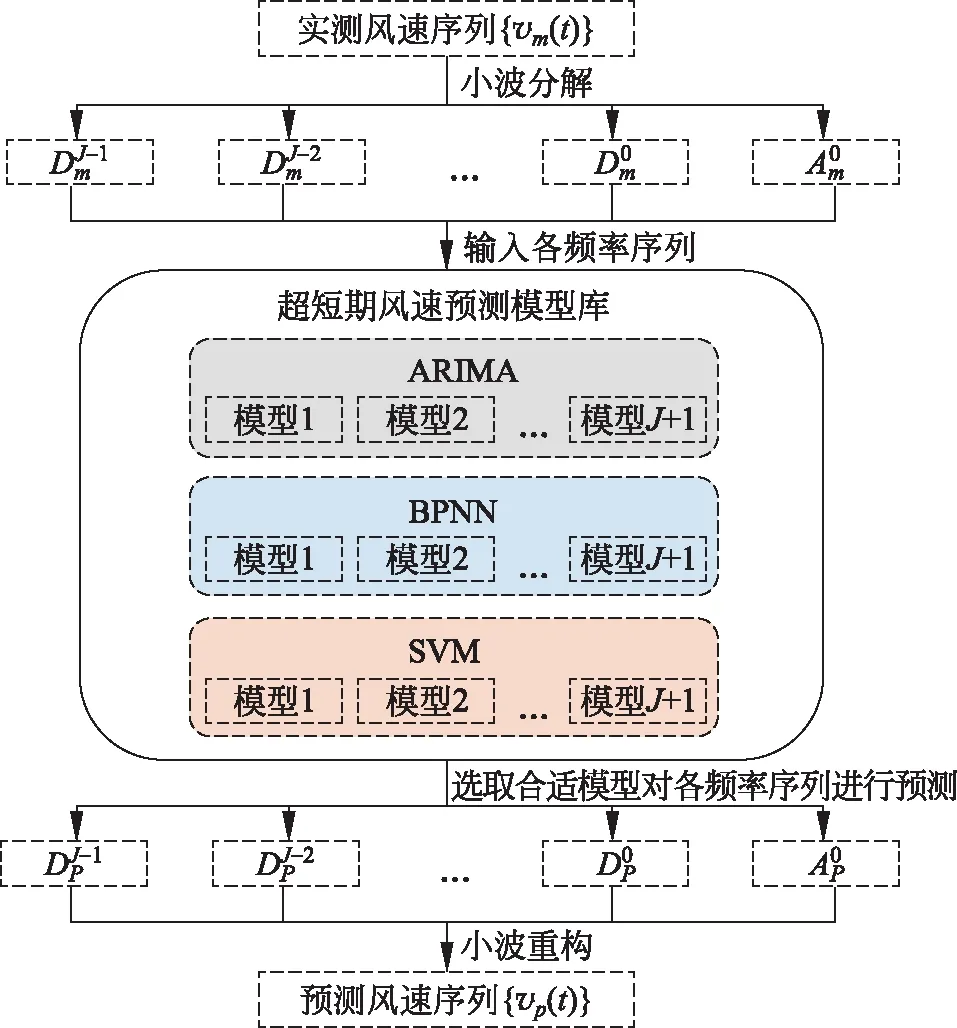
图3 超短期风速混合模型组合预测流程图Fig.3 Process of ultra-short-term wind speed combined prediction with a hybrid model

Step2: 基于ARIMA，BPNN与SVM三种方法，对各频率序列分别建立超短期预测模型库，其中包含3×(J+1)模型。

Step3: 基于相应的预测误差评价指标，对比分析各模型在各频率序列的预测结果，依据各频率序列特点分别选取合适模型进行预测。

2.2 预测误差评价指标

为评估各风速预测模型的预测精度，本文中采用均方根误差(root mean square error, RMSE)与平均绝对误差(mean absolute error, MAE)作为评价指标，单位均为m/s。其中RMSE侧重于描述模型在一段时间内的整体误差，MAE侧重于描述模型的实时偏差，计算公式分别如式(8)、式(9)所示。

式中：vm(t),vp(t)分别为t时刻的实测风速与预测风速，m/s；N为预测时长内的风速数据量。

3 实例验证

以我国北部和南部两个风电场的实际测风数据作为本文的实验数据，时间分辨率为10 min，时间长度为1年，分别记做风电场1和风电场2。为验证本文中所提方法的有效性与精确性，分别在1 h与4 h预测时间尺度下，基于ARIMA，BPNN与SVM三种模型，将所提方法与传统超短期风速预测方法，包括直接预测法与单一模型组合预测法进行对比分析。

3.1 1 h预测时长

以实际测风数据为依据，首先采用持续法与直接预测法对其进行超短期风速预测，预测结果如表1所示。从表1中可以看出，在 1h预测时长下，无论选用何种评价指标，直接应用ARIMA，BPNN与SVM三种模型进行超短期风速预测时，其预测误差均与持续法所得预测误差基本相同，甚至精度还略低于持续法。

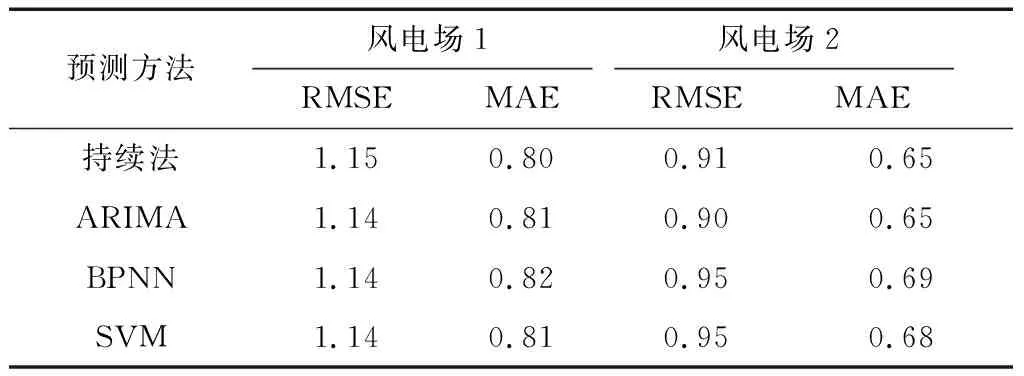
表1 持续法与直接预测法预测结果(1 h预测时长)Table 1 Results of persistence method and direct prediction methods (1 h time horizon) m/s

由于风速时间序列可看作是由多种频率序列组合而成，为提高风速预测精度，可首先对原始风速序列进行小波分解以提取其各频率序列的隐藏特征，而后对各频率序列进行建模预测，最后再将各频率序列的预测结果进行小波重构，得出最终超短期风速预测结果。如何选取合适的小波分解层数对预测精度与预测速度至关重要，分解层数过小可能会使各频率序列包含较多的干扰信号，无法准确提取其隐藏特征；分解层数过大则会导致需要建模预测的序列增多，降低预测速率。因此，在1 h预测时长下，分别以RMSE和MAE为评价指标，对各模型组合预测精度随小波分解层数的变化趋势进行分析，如图4所示。其中“ARIMA”，“BPNN”，“SVM”分别表示基于小波分解的传统预测方法的预测结果，即分别以ARIMA，BPNN和SVM作为基本模型的单一模型组合预测结果，“混合模型”表示同时以ARIMA，BPNN和SVM作为基本模型的基于小波分解的混合模型组合预测结果。

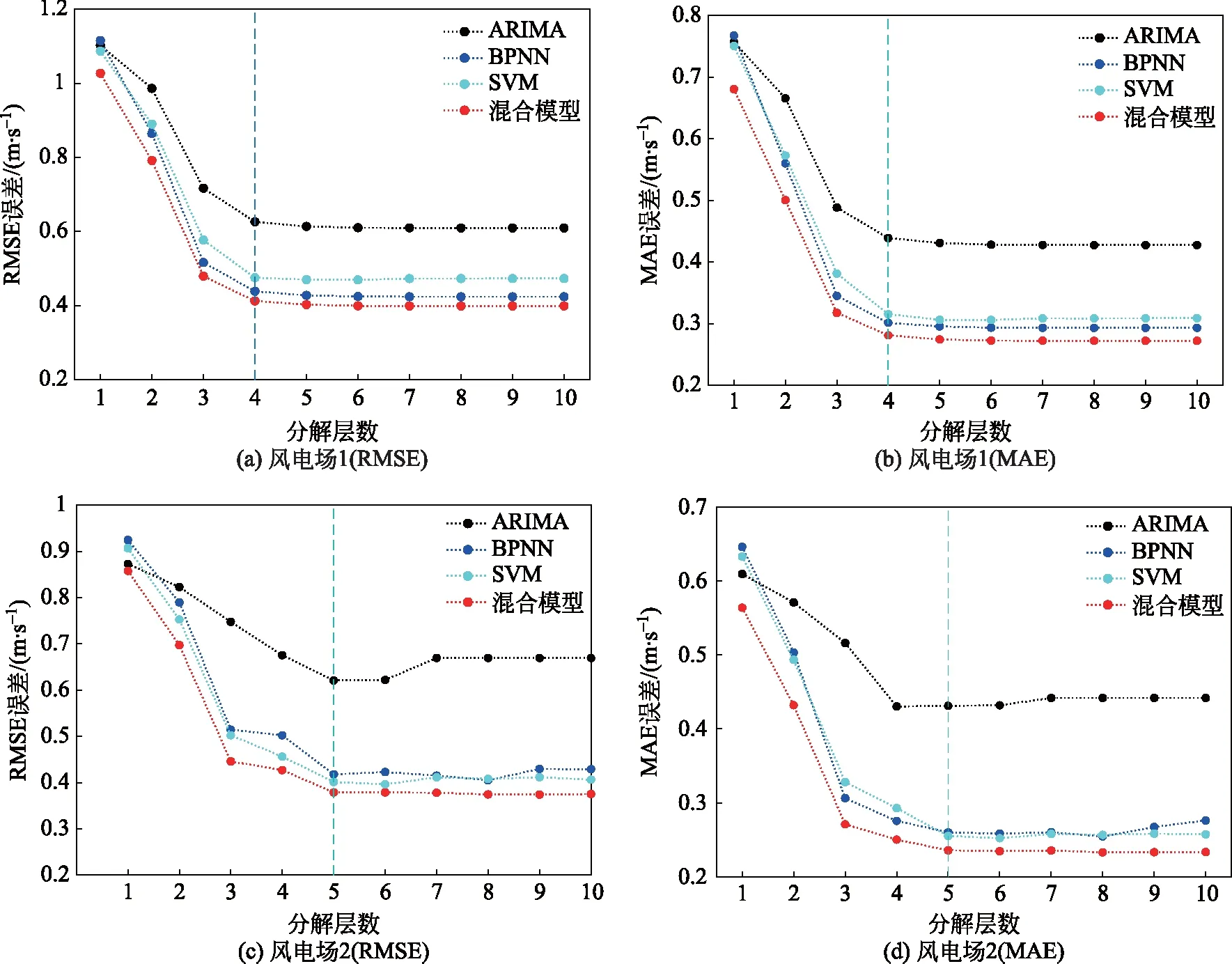
图4 在不同分解层数下各种预测方法的预测精度(1 h预测时长)Fig.4 Comparison of wind speed prediction accuracy under different decomposition levels (1 h time horizon)

从图4可以看出，在2个风电场中，无论是以RMSE还是以MAE为预测误差评价指标，在不同小波分解层数下，本文所提方法(即基于小波分解的混合模型组合预测方法)与传统基于小波分解的预测方法相比，预测精度均有所提高。对于风电场1，当分解层数为4层时，各方法预测误差基本保持稳定；对于风电场2，当分解层数为5层时，各方法预测误差基本保持稳定，但以ARIMA作为基本模型的组合预测方法，当分解层数达到7层时，其预测精度随分解层数的增加而有所降低。因此，在1 h预测时长下，同时考虑预测精度与预测速度时，对于风电场1，最佳小波分解层数为4层；对于风电场2，最佳小波分解层数为5层。统计最佳小波分解层数下各方法的风速预测精度，如表2。

从表2中可以看出，当预测时长为1 h时，在最佳小波分解层数下，本文中所提方法与传统方法中预测误差最低方法相比，以RMSE为预测误差评价指标时，预测精度可提高6.8%(风电场1)、5.6%(风电场2)；以MAE为预测误差评价指标时，预测精度可提高6.7%(风电场1)、7.7%(风电场2)。结合表1中所得结果，本文所提方法与持续法相比，以RMSE为预测误差评价指标时，预测精度可提高64.3%(风电场1)、58.2%(风电场2)；以MAE为预测误差评价指标时，预测精度可提高65.2%(风电场1)、63.1%(风电场2)。

为分析本文中所提方法在1 h预测时长下、不同月份预测的稳定性，现以MAE为预测误差评价指标，计算最佳小波分解层数下各方法在各月的预测误差，如图5所示。从图5中可以看出，在同一风电场各方法预测误差的月变化趋势基本相同。在风电场1，“ARIMA”、“BPNN”、“SVM”、“混合模型”在不同月份预测误差的变化幅值分别为0.101、0.080、0.096、0.075 m/s，标准差分别为0.035、0.026、0.032、0.023 m/s；在风电场2，“ARIMA”、“BPNN”、“SVM”、“混合模型”在不同月份预测误差的变化幅值分别为0.441、0.222、0.132、0.124 m/s，标准差分别为0.125、0.058、0.038、0.031 m/s。可以看出，与传统单一模型组合预测方法相比，本文所提方法在不同月份的预测稳定性更好。

表2 在最佳小波分解层数下各种风速预测方法的预测精度(1 h预测时长)Table 2 Comparison of wind speed prediction accuracy under the best decomposition level(1h time horizon) m/s

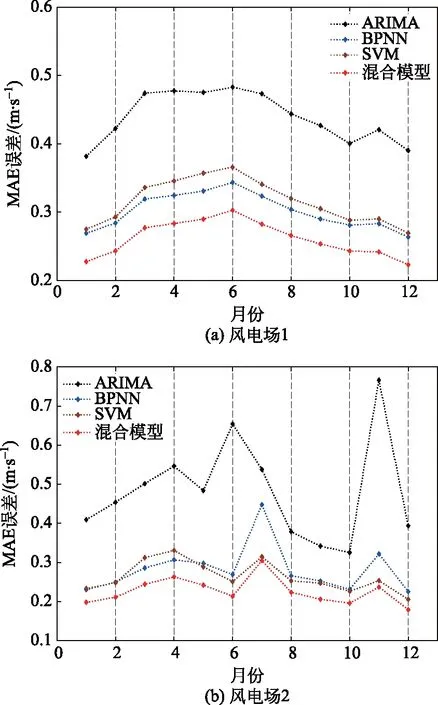
图5 在最佳小波分解层数下各种风速预测方法的预测精度月变化曲线(1 h预测时长)Fig.5 Comparison of wind speed prediction accuracy in different months under the best decomposition level (1 h time horizon)

3.2 4 h预测时长

以实际测风数据为依据，在4 h预测时长下，首先采用持续法与直接预测法对其进行超短期风速预测，结果如表3所示。从表3中可以看出，直接应用ARIMA，BPNN与SVM三种模型进行超短期风速预测所得结果与持续法所得结果相比，采用RMSE为预测精度评价指标时，其预测精度仅略高于持续法；采用MAE为预测精度评价指标时，仅直接应用ARIMA模型所得预测结果精度略高于持续法。

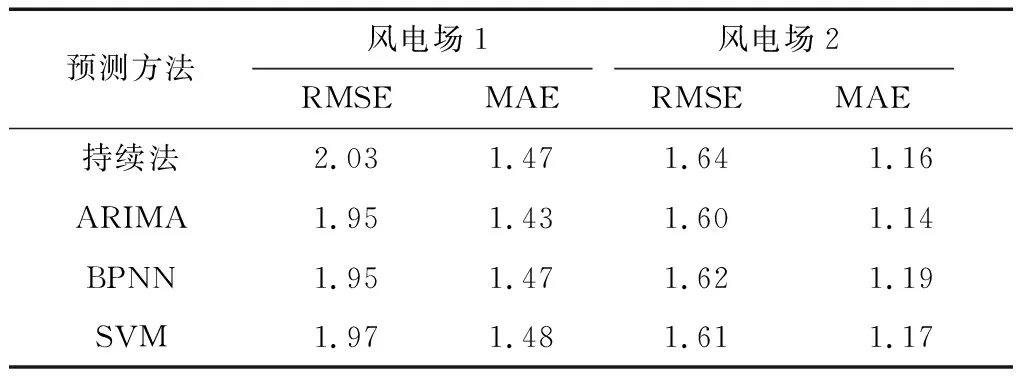
表3 持续法与直接预测法预测结果(4 h预测时长)Table 3 Results of persistence method and direct prediction methods (4 h time horizon) (m/s)

为提高4 h预测时长下超短期风速的预测精度，拟采用基于小波分解的组合预测方法进行预测。此方法与3.1中1 h预测时长下所面临的关键问题相同，均为如何选取合适的小波分解层数。因此，在4 h预测时长下，分别以RMSE和MAE为评价指标，对各模型组合预测精度随小波分解层数的变化趋势进行分析，如图6所示。从图6可以看出，在两种预测精度评价指标下，本文所提方法在不同小波分解层数下与传统基于小波分解的预测方法相比，预测精度均有所提高。对于风电场1，当分解层数为6层时，各方法预测误差基本保持稳定；对于风电场2，当分解层数为6层时，各方法预测误差基本保持稳定，但当分解层数大于6层时，以BPNN或SVM为基本模型的组合预测方法其预测精度随分解层数的增大出现波动。因此，在4 h预测时长下，同时考虑预测精度与预测速度的条件下，对于风电场1，最佳小波分解层数为6层；对于风电场2，最佳小波分解层数为6层。统计最佳小波分解层数下各方法的风速预测精度，如表4所示。

从表4中可以看出，当预测时长为4 h时，在最佳小波分解层数下，本文中所提方法与传统方法中预测误差最低方法相比，以RMSE为预测误差评价指标时，预测精度可提高7.4%(风电场1)、5.3%(风电场2)；以MAE为预测误差评价指标时，预测精度可提高5.3%(风电场1)、6.1%(风电场2)。

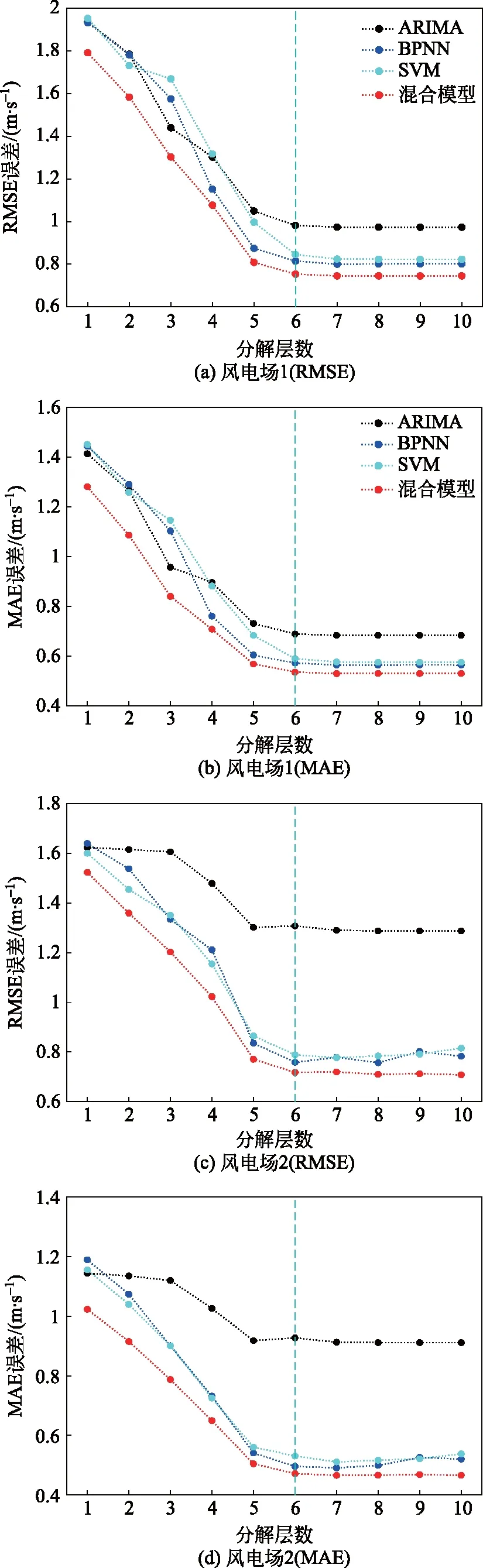
图6 在不同分解层数下各种预测方法的预测精度(4 h预测时长)Fig.6 Comparison of wind speed prediction accuracy under different decomposition levels(4 h time horizon)

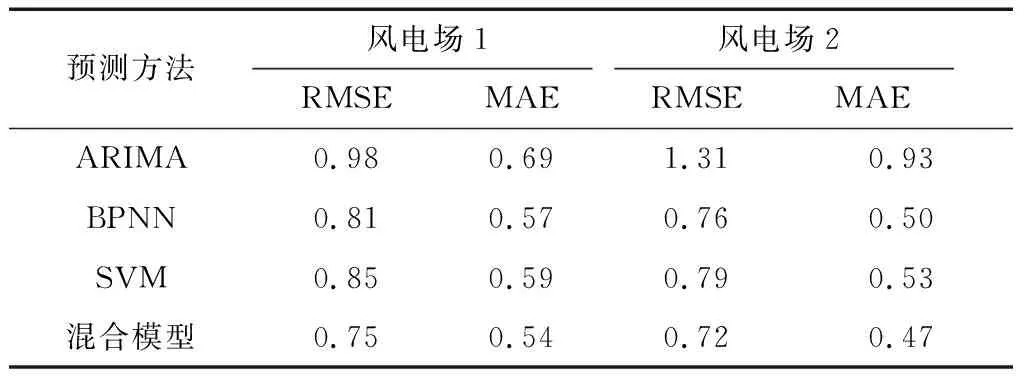
Table 4 Comparison of wind speed prediction accuracy under the best decomposition level(4 h time horizon) m/s

结合表3中所得结果，本文所提方法与持续法相比，以RMSE为预测误差评价指标时，预测精度可提高63.1%(风电场1)、55.3%(风电场2)；以MAE为预测误差评价指标时，预测精度可提高63.3%(风电场1)、59.5%(风电场2)。

为分析本文中所提方法在4 h预测时长下、不同月份预测的稳定性，现以MAE为预测误差评价指标，计算最佳小波分解层数下各方法在各月的预测误差，如图7所示。与预测时长为1 h时，在最佳小波分解层数下各方法预测精度的月变化曲线(图5)相比，同一风电场各方法预测误差的月变化趋势有一定的差异，如在风电场2，以ARIMA为基本模型的组合预测方法其月变化与其他三种方法有明显不同。在风电场1，“ARIMA”、“BPNN”、“SVM”、“混合模型”在不同月份预测误差的变化幅值分别为0.186、0.146、0.162、0.111 m/s，标准差分别为0.061、0.050、0.052、0.040 m/s；在风电场2，“ARIMA”、“BPNN”、“SVM”、“混合模型”在不同月份预测误差的变化幅值分别为0.507、0.336、0.296、0.224 m/s，标准差分别为0.166、0.112、0.088、0.079 m/s。可以看出，与传统单一模型组合预测方法相比，本文所提方法在不同月份的预测稳定性更好。

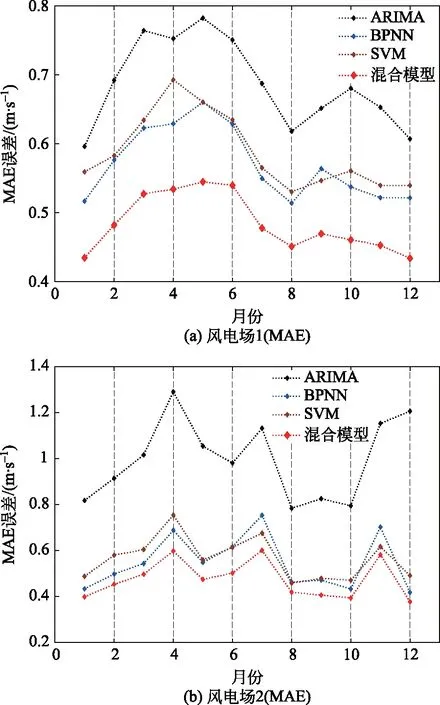
图7 在最佳小波分解层数下各种风速预测方法的预测精度月变化曲线(4 h预测时长)Fig.7 Comparison of wind speed prediction accuracy in different months under the best decomposition level(4 h time horizon)

4 结论

1) 在同时考虑预测精度与预测速率的条件下，当预测时长为1 h时，最佳小波分解层数为4～5层；当预测时长为4 h时，最佳小波分解层数为6层。

2) 与传统直接预测方法和单一模型组合预测方法相比，本文中所提方法在不同预测时长下均具有较高的预测精度。以MAE为预测误差评价指标，本文中所提方法与持续法相比，在1 h预测时长下，预测精度可提高65.2%(风电场1)、63.1%(风电场2)；在4 h预测时长下，预测精度可提高63.3%(风电场1)、59.5%(风电场2)；与传统方法中预测误差最低方法相比，在1 h预测时长下，预测精度可提高6.7%(风电场1)、7.7%(风电场2)；在4 h预测时长下，预测精度可提高5.3%(风电场1)、6.1%(风电场2)。

3) 与传统单一模型组合预测方法相比，本文所提方法在不同预测时长下均具有更高的月预测稳定性。

致谢

本文由中国大唐集团有限公司赤峰分公司科技项目“集中式风电功率预测及风电场功率优化分配控制算法研究与系统开发”资助，谨此致谢。