基于蒙特卡洛模拟的连续下降运行间隔分析*

朱海波 张军峰 刘 杰

(南京航空航天大学民航学院 南京 210016)

0 引 言

近年来，航空运输业的蓬勃发展为人们出行提供了便捷。然而，随着空中交通流量的持续增长，使燃油消耗、废气排放、噪声污染等问题日益凸显，极大地影响了航空运输业的可持续发展，因此，波音公司与麻省理工于美国路易斯维尔机场率先开展连续下降进近(CDA)研究。为期2周的试飞验证表明，CDA程序能够有效地实现节能、减排与降噪[1]。

鉴于CDA程序的显著优势，国际民航组织(ICAO)于2010年丰富其内涵,拓宽其外延，将CDA程序扩展为连续下降运行(CDO)[2]，并给出如下定义：“CDO是在空域设计、程序设计与空中交通管制的通力协作下，保障进场航空器以闲置推力、低阻构型实现持续下降运行”。进一步，国际民航组织的“航空系统组块升级”(ASBU)战略，将CDO作为未来提高下降剖面的灵活性与效率的重要模块。为此，各国学者纷纷投入到CDO的效果评估与剖面设计研究中。Coppenbarger等[3]验证了Boeing777机型在实施连续下降运行时的节能、减排与降噪效果；Jin等[4]从航空器性能角度深入剖析了CDO程序降低燃油消耗的内在机理；吴文洁[4]等考虑实际气象条件，结合BADA模型，提出了飞机的燃油消耗量和污染物排放量计算方法，验证了Boeing763机型在实施CDO时的节能减排效果。Khardi[6]利用Hamilton-Jacobi-Bellman方程实现CDO最优垂直剖面设计；宫峰勋等[7]以时间最优为目标，基于高斯伪谱法优化CDO的垂直剖面；Park等[8]对比了飞行管理系统(FMS)生成的垂直剖面、时间最优垂直剖面以及燃油最优垂直剖面的关系，从而指导CDO的相关参数设计；Liu等[9]从改变水平轨迹的角度出发，探讨了CDO实际运行时的冲突解脱方案。

虽然CDO程序的优势明显，但CDO固有的运行特点要求：进场航空器需按照FMS生成的水平航迹与垂直剖面，在自动驾驶仪与自动油门的引导下实现持续下降运行。该特点势必要求进近管制员尽可能地不影响飞行剖面，从而将管制职能由“间隔调配”向“间隔监控”过渡，如此，实施连续下降运行的进场航空器进入终端空域的管制移交间隔确定就显得尤为关键。若移交间隔过大，则限制空域容量，加剧进场延误，与CDO的初衷背道而驰[10]；若移交间隔过小，则增加工作负荷，影响安全运行。由于空中交通管制的首要任务在于防止航空器相撞，因此碰撞风险模型[11]与冲突风险模型[12]是间隔确定的主要模型。然而究其本质，主要是基于仿真模拟研究航空器之间的安全间隔，如Ghoneim等[13]利用仿真模拟产生交通流，以安全指标为优化目标，利用随机优化算法获得最小管制间隔。同时，由于进场航空器连续下降运行时，航空器机型、航空器重量、空域内风场信息均存在着不确定性，此时蒙特卡洛模拟仿真能够有效地解决此类问题，如Blom等[14]通过构建多智能体模拟管制与飞行之间的通信，进而结合蒙特卡洛模拟分析大流量下航空器的间隔配备。

综上所述，目前鲜有针对连续下降运行的安全间隔分析。因此，笔者一方面提出连续下降运行的航空器垂直剖面的生成模型与求解算法，另一方面考虑连续下降运行中的不确定性，提出基于蒙特卡洛模拟的安全间隔分析方法，从而实现管制移交间隔的科学评估。如此，可以确保在保障飞行安全的前提下，有效实现进场航空器节能、减排与降噪的目的。

1 连续下降运行的航迹生成

1.1 “闭合式”连续下降运行

连续下降运行旨在保障进场航空器以闲置推力、低阻构型实现持续下降，因此垂直剖面的设计是基础与关键。国际民航组织将连续下降运行分为“闭合式”与“开放式”2类。从航路阶段实施“闭合式”的连续下降运行示意图如图1所示，包含了8个阶段：减马赫数巡航；等马赫数下降；等校正空速下降；等下降率减速下降；校正空速250 kt下降；减速下降；调整构型，减速下降；固定航径角最后进近。

图1 “闭合式”CDO典型垂直剖面示意图Fig.1 Schematic diagram for vertical profile of “closed-path” CDO

由于“闭合式”连续下降运行，一方面需要区域与进近管制之间有效协调，另一方面需要航班落地时隙的合理分配，上述需求离不开管制决策支持[15]，因此，现阶段连续下降运行的实施往往以从终端空域开始的“开放式”CDO类型，至IAF点结束。此时大致可以分为5个阶段：①进入终端空域，等CAS平飞；②等CAS下降；③减速至250 kt下降；④等CAS下降；⑤减速至IAF处限制速度下降。

1.2 “开放式”连续下降运行

从终端空域开始的“开放式”CDO的水平轨迹与垂直剖面示意图如图2所示。图2同时标明了1.1节所提及的垂直剖面5个阶段对应的推力设置与航空器构型。相对于垂直剖面，连续下降运行的水平轨迹与常规运行类似，主要可以分为直线航段与转弯航段。

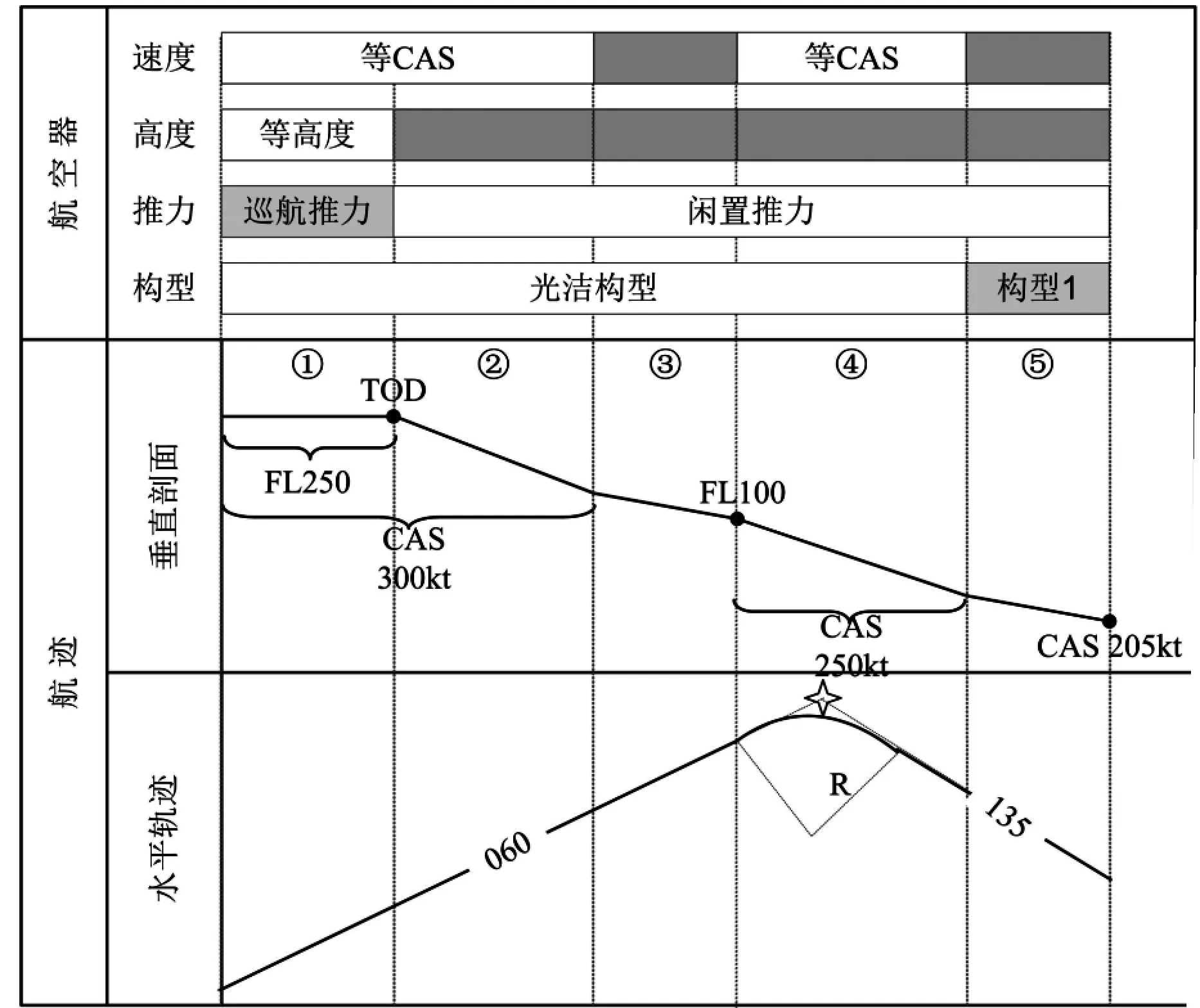
图2 “开放式”CDO水平轨迹与垂直剖面示意图Fig.2 Schematic diagram for lateral track and vertical profile of “open-path” CDO

1.3 连续下降运行的航空器模型

连续下降运行的航空器模型见式(1)～(5)。

(1)

(2)

(3)

(4)

(5)

式中:m,T,D,L分别为航空器的质量、推力、阻力与升力；γ,μ,χ分别为飞行航径角、空气动力学侧倾角与偏航角；VTAS,h,s分别为航空器飞行的真空速、高度与距离;Uw与Vw为风速的正北与正东向分量；fFuel为燃油消耗率。

由图2可知，“开放式”CDO的垂直剖面主要集中于3个方面：等CAS平飞、等CAS下降与减CAS下降(也即固定下降率下降)，此时可以对模型作进一步简化。

1) 等CAS平飞。此时，航空器真空速与校正空速存在如下函数关系。

(6)

式中:κ=1.4,p0=101 325 Pa,ρ0=1.225 kg/m3,p与ρ为相应高度处大气气压与密度。

2) 等CAS下降。此时，航空器真空速会随着高度降低而逐渐减小，通过引入能量分配系数(ESF)[16]来体现航空器在下降过程中动能与势能的转换关系，则连续下降运行的高度剖面为

(7)

式中：f(M)为能量分配系数，各机型参数、推力T、阻力D，以及能量分配系数的计算，参见文献[16]。

(8)

(9)

其中:const.为恒定下降率，取各类机型的正常下降率。

求解上述给定模型时，由于无法预知图2中的TOD点位置(①和②之间)，以及无法确定减速时机(②与③，④与⑤之间)，因此本文采用基于四阶龙格库塔的反向积分实现连续下降运行的航迹生成。

2 连续下降运行的间隔分析

连续下降运行要求进场航空器在自动驾驶仪与自动油门的引导下，按照FMS生成的参考轨迹，实现连续下降。为了使管制员尽可能地不影响飞行剖面，同时不降低空域运行容量，需要合理设置管制移交间隔。然而，由于先后进场航空器的机型配比各异，不同时段的风速风向迥然，而且航空器重量与速度也不同，因此到达IAF的时间也千差万别。

图3描述了进场航空器对间隔演化规律，其中前后机的位置与时间变化曲线的不确定性如阴影部分所示。

对于图3中IAF处间隔的不确定性，本文拟采用蒙特卡洛模拟实施评估与分析。蒙特卡洛模拟以概率统计理论为基础，在不确定性问题分析领域应用广泛。该方法假定随机变量的概率分布已知，通过随机采样产生输入变量，然后进行模拟，随即获得输出。最后针对输出实施统计分析，能够拟合输出结果的概率分布。鉴于风变化轮廓可被视为随着高度变化的随机过程[17]，而且航空器进场速度与质量也服从一定分布。如此，可以基于蒙特卡洛模拟实现连续下降运行的间隔分析，具体流程如图4所示。

图3 进场航空器对间隔演化示意图Fig.3 Schematic diagram for separation evolution of arrival aircraft

在基于蒙特卡洛模拟实施CDO的间隔分析时,首先，根据航图确定连续下降运行的水平航迹与垂直剖面的限制；其次，考虑进场航空器的机型，确立性能参数、速度分布、重量分布以及运行空域内的风速与风向分布；再次，利用随机采样产生上述变量，并将其引入连续下降运行的航空器模型，基于四阶龙格库塔的反向积分生成连续下降运行的航空器四维轨迹；最后，考虑现行管制移交间隔下，分析不同参数影响的进场航空器在IAF点处的时空演化特性，评估管制移交间隔的安全性。

图4 基于蒙特卡洛模拟的间隔分析示意图Fig.4 Schematic diagram of separation analysis based on Monte Carlo simulation

3 仿真与分析

3.1 仿真场景构建

广州白云国际机场于2016年12月8日开始CDO的试运行工作，本仿真以白云机场北向运行为例，针对ATAGA进场的连续下降运行，选取典型重型机(A332)与中型机(A320)实施仿真。

航空器的速度和质量将影响航迹生成的垂直剖面[18]：移交点处的速度往往由移交协议规定，然而实际运行中由于飞行操作、外部环境等因素，移交速度将不可避免的存在波动；航空器质量与业载、燃油息息相关，即便是同一机型，每个航班也不尽相同。本文仿真基于BADA提供的基本参数、结合管制员与飞行员的建议、同时考虑机型的最大着陆质量与速度包络，设置A320机型在进港点处的速度、质量以及IAF处的速度满足如下分布。

风速与风向主要分析通过分析广州终端空域ATAGA点气象信息，构建相应的风速、风向的概率分布，如图5所示。

图5 ATAGA处风速、风向剖面示意图Fig.5 Schematic diagram of wind profiles at ATAGA fix

3.2 航迹生成分析

在实施间隔分析之前，为了考察本文提出的CDO垂直剖面生成模型的有效性，将生成的高度剖面、速度剖面与飞行模拟试验(2016年9月14日于珠海，如图6所示)进行对比分析。使用如下设置：A320机型，ATAGA处质量60 000 kg,速度300 kt，IAF处速度205 kt，静风条件。对比结果如图7所示。

图6 飞行模拟试验Fig.6 Flight simulator test

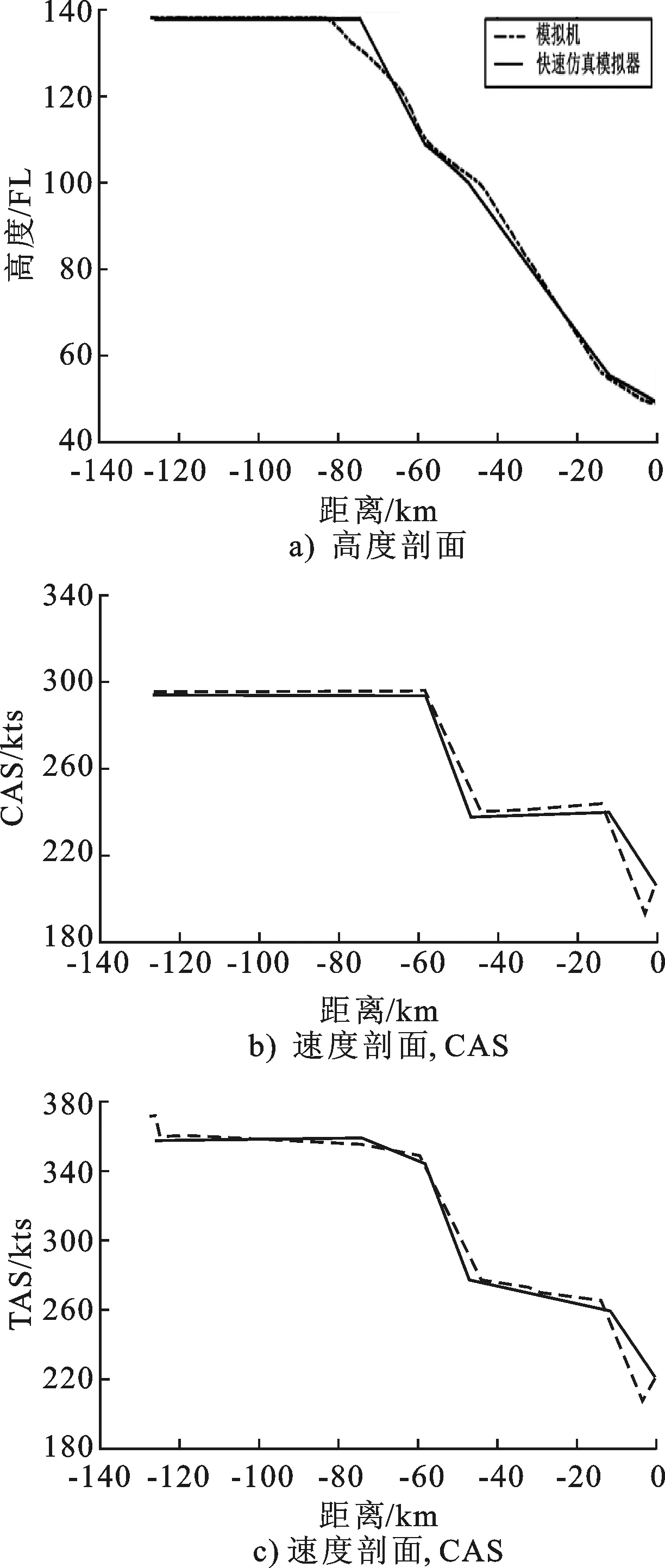
图7 垂直剖面对比示意图Fig.7 The comparison of speed profile

不难发现，本文设计的快速仿真模拟器与模拟机生成的高、速度剖面基本吻合，仅在高度剖面中TOD点的位置和速度剖面中IAF点前的速度存在一定差异，表明本文设计的连续下降运行的垂直剖面生成模型能够有效地反映实际运行的特点。

3.3 安全间隔分析

ATAGA进港时，现行管制移交间隔为30 km。前机A332(H)、后机A320(M)为例，进行间隔分析，基于蒙特卡洛仿真，采用3.1所述参数，实施5 000次仿真，结果如图8所示。

图8 基于蒙特卡洛仿真的航迹误差与间隔示意图Fig.8 Trajectory variations and separation based on Monte Carlo simulation

同一时刻，前机最小飞行距离与后机最大飞行距离之间的差值(图8中A332航迹包络的下界与A320航迹包络上界之间的差值)，即连续航空器对间的最小间隔。取某一次仿真为例，如图9所示，后机追赶前机效应明显，由初始的30 km间隔，在无任何干预的情况下，间隔逐渐缩小至14 km左右。

图9 连续航空器对间最小水平间隔示意图Fig.9 Minimum lateral separation between consecutive aircraft pairs

针对上述5 000次蒙特卡洛模拟仿真，进行最后间隔的概率统计分析，结果如图10所示。可知，IAF点处航空器之间的间隔服从均值为15.1 km，方差为1.12的正态分布，且IAF点处间隔大于12 km的概率为99.78%。因此，现行管制移交间隔能够保障连续下降运行的安全实施。

图10 IAF点处连续航空器对间隔概率密度示意图Fig.10 The probability density of separation between consecutive aircraft pairs at IAF

3.4 分析与讨论

根据上述仿真，可以得出如下结论。

1) 采用本文提出的垂直剖面生成模型和求解方法，能够准确并有效地生成各类机型在连续下降运行时的垂直剖面。

2) 通过对比图7所示的结果，可以发现本文提出的垂直剖面生成模型和求解方法的缺陷在于，将航空器模型简化为瞬时运动模型，未考虑航空器构型缓变的特性。

3) 本文提出的基于蒙特卡洛模拟的间隔分析方法，由于考虑了风速风向、航空器重量与速度等的不确定性，能够得到航空器对之间间隔的时空分布特性，且满足安全间隔的置信度。

4) 本文提出的方法，可以简单推广到其他空中交通的间隔分析与安全评估领域，且优于其他确定型的分析评估方法。

4 结束语

本文针对连续下降运行程序，研究了其垂直、水平剖面，且构建了相应的运动模型，并与飞行模拟进行了对比。在此基础上，模拟出风、航空器速度和质量的不确定性对于航空器航迹的影响，提出了一种基于蒙特卡洛模拟的间隔分析方法。案例分析表明，考虑上述不确定性因素的影响，现行的管制移交间隔仍能保障连续下降运行的安全实施，但现行管制移交间隔能否进一步缩减，以及缩减到何种程度，如何考虑不同方向进港航班实施连续下降运行的管制辅助决策，是未来需要深入研究的问题。