基于变分模态分解和复杂度分析的水电机组振动信号特征提取

胡 晓，王 昕，黄建荧，刘 东，肖志怀

(1.武汉大学 流体机械与动力工程装备技术湖北省重点实验室，湖北 武汉430072；2.国网福建水口发电集团有限公司，福建 福州 350004)

0 引 言

为保障水电机组安全可靠运行，需要进行水电机组状态监测与故障诊断，从而做出合理的维修决策[1]。水电机组的振动信号中通常蕴含有其运行状态的重要信息[2]，因此可通过提取振动信号的特征值来进行故障识别。对水电机组振动信号进行有效处理，分析并提取反映其运行状态的特征，是水电机组运行状态评估、诊断的基础，直接关系到后续水电机组故障诊断结果的准确性及可靠性。

水电机组结构复杂、存在多部件耦合振动、振动噪声干扰大等情况，采集到的振动信号具有非平稳、非线性等特点，致使故障征兆不明显，故障特征难以提取[3]。目前，水电机组振动信号特征提取常用的时频分析方法有小波分解、小波包分解、EMD分解等[2]。然而，这些方法也存在一些不足，如小波分解的效果受小波基的选择以及分解层数的影响较大[4]；EMD方法存在模态混叠问题，导致瞬时频率的物理意义不明确[5～6]。为了弥补原有方法的不足，文献[7]提出了变分模态分解VMD(Variational Model Decomposition)，该方法根据经典维纳滤波、Hilbert变换以及频率混合的原理，将原始信号分解为一系列有带宽限制和中心频率的固有模态函数(IMF)，是一种自适应时频分析方法[7～9]。复杂度分析源于1965年提出的算法复杂度的概念，是一种非线性动力学的分析方法，适合对非线性、非平稳信号的分析处理[10]。复杂度的概念通常指的是Lempel-Ziv复杂度(LZC)，该算法可以表征时间序列里出现新模式的速率，需要的数据量少且具有一定抗干扰能力。

本文在当前研究的基础上，提出一种基于变分模态分解与复杂度分析的信号特征提取方法，并运用该方法对转子试验台和水电站机组的振动信号进行特征提取和故障识别，试验结果表明基于变分模态分解与复杂度分析的特征提取方法对水电机组不同运行状态具有较好的区分度。

1 基本原理

1.1 变分模态分解

变分模态分解[7]中将“模态”定义为有带宽限制的调频调幅函数，VMD算法的原理主要涉及了三个重要概念，即经典维纳滤波、希尔伯特变换和频率混合。

(1)变分问题的构造。变分问题的求解过程为求K个本征模态函数uk(t)，使每个模态函数的估计带宽之和最小，其约束条件为所有本征模态函数相加之和为原输入信号[11]，变分问题模型可表示为如下式[11]：

(1)

式中：ωk为每个模态对应的中心频率。

(2)变分问题的求解。引入二次惩罚因子α和拉格朗日乘法算子λ(t)，变约束问题为非约束性变分问题，二次惩罚因子α的作用是在受高斯噪声干扰的情况下保证信号的重构精度，λ(t)的作用是保持约束条件的严格性，

(2)

同理，得到中心频率的更新公式：

(3)

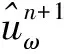
变分模态分解算法计算流程：

Step2：n=n+1，执行整个循环；

Step3：根据式(2)和式(3)更新uk和ωk；

Step4：k=k+1，重复Step3，直至k=K；

Step5：根据下式更新λ：

要想从根本上提高衡阳市水稻生产水平，不仅要建立完整的种植管理监督机制，也要结合衡阳市实际情况，优化水稻种植技术。当地政府要组织相关部门对农户进行水稻种植技术的培训和指导，确保农户能真正体会到新技术类型产生的经济效益，从而推动水稻种植管理发展进程，实现经济效益和环保效益的共赢。

(4)

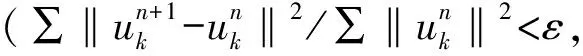
1.2 复杂度分析

Lempel-Ziv复杂度的计算原理[10]如下：设长度为n的某时间序列按Lempel-Ziv算法得出{S(i)}中互异的子串个数为c(n)，当n→∞，c(n)会趋向于定值n/logLn，则归一化复杂度的计算公式为：

(5)

从上述算法中可以看出，若子序列段按时间顺序较多次的重复在其之前的子序列段，则该序列的复杂度较低；若子序列段按时间顺序较少次的重复在其之前的子序列段，则该序列的复杂度较高。序列的复杂度越大，说明序列中的周期成分越少，序列越无规律，趋近于随机状态，序列包含的频率成分越丰富，系统的复杂度也越高；序列的复杂度越小，说明序列中周期成分越多，越趋于周期状态，序列包含的频率成分越少，系统的复杂度也越低。

2 基于变分模态分解和复杂度分析的振动特征提取

由于振动信号经过变分模态分解后得到的每个IMF分量上带有不同的状态信息。故基于变分模态分解和复杂度分析的振动特征提取方法的思路是首先对水电机组振动信号进行变分模态分解，然后计算各不同模态分量的复杂度值，并利用不同模态分量的复杂度值组成特征向量集如下：

C={ILZC1,ILZC2,…,ILZCn}

(6)

式中：n代表变分模态分解得到的IMF的个数。

为验证所提出的基于变分模态分解和复杂度分析的振动信号特征提取方法的有效性，分别从转子实验台和某水电机组状态监测系统获取振动信号进行特征提取和分析。

2.1 试验信号分析

利用转子振动试验台分别模拟碰磨、正常、不平衡、不对中四种状态，测取相关振动信号，经过小波阈值降噪后与降噪前的信号对比如图1所示。

从图1中可以看出，对原始振动信号进行降噪后仍难以得到信号的特征，无法区分转子的运行状态。对正常状态的振动信号进行变分模态分解，结果如图2所示。为了避免出现模态混叠和中心频率重叠，通过计算变分模态分解得到的各个模态分量与原始信号的相关系数来得到最佳模态分量的分解个数K，并设定阈值为5%。采用同样的方法得出其他运行状态下的最佳变分模态分解个数如表1所示。

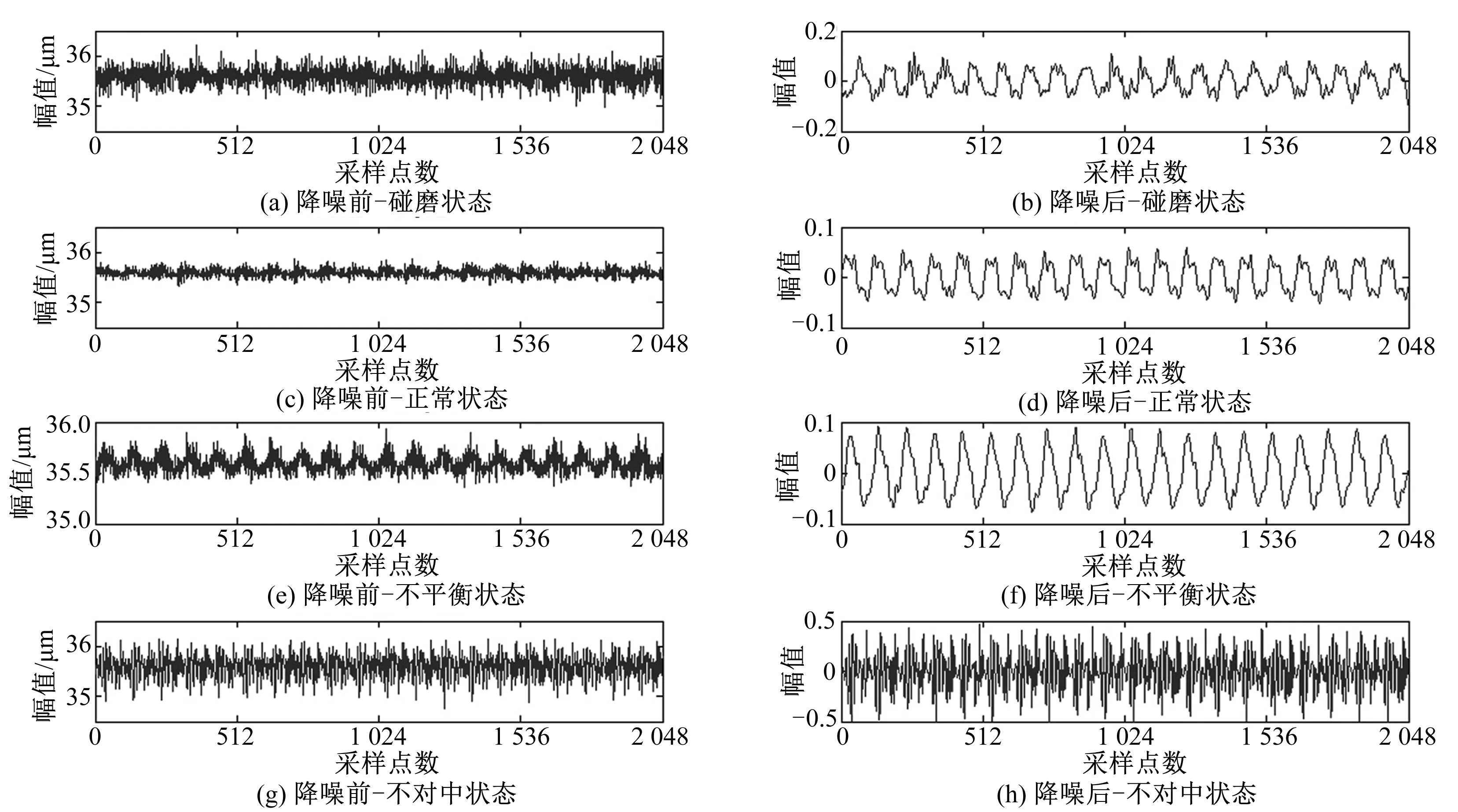
图1 不同运行状态下降噪前后的信号对比图Fig.1 Comparison of signals before and after noise reduction in different operating states

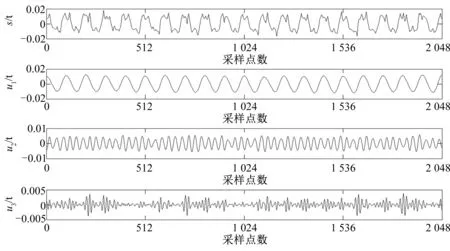
图2 正常状态下变分模态分解图Fig.2 Variational mode exploded view under normal operating conditions

表1 采用变分模态分解的不同工况下振动信号的IMF分量个数Tab.1 The number of IMF functions of vibration signals under different operating conditions using variational mode decomposition

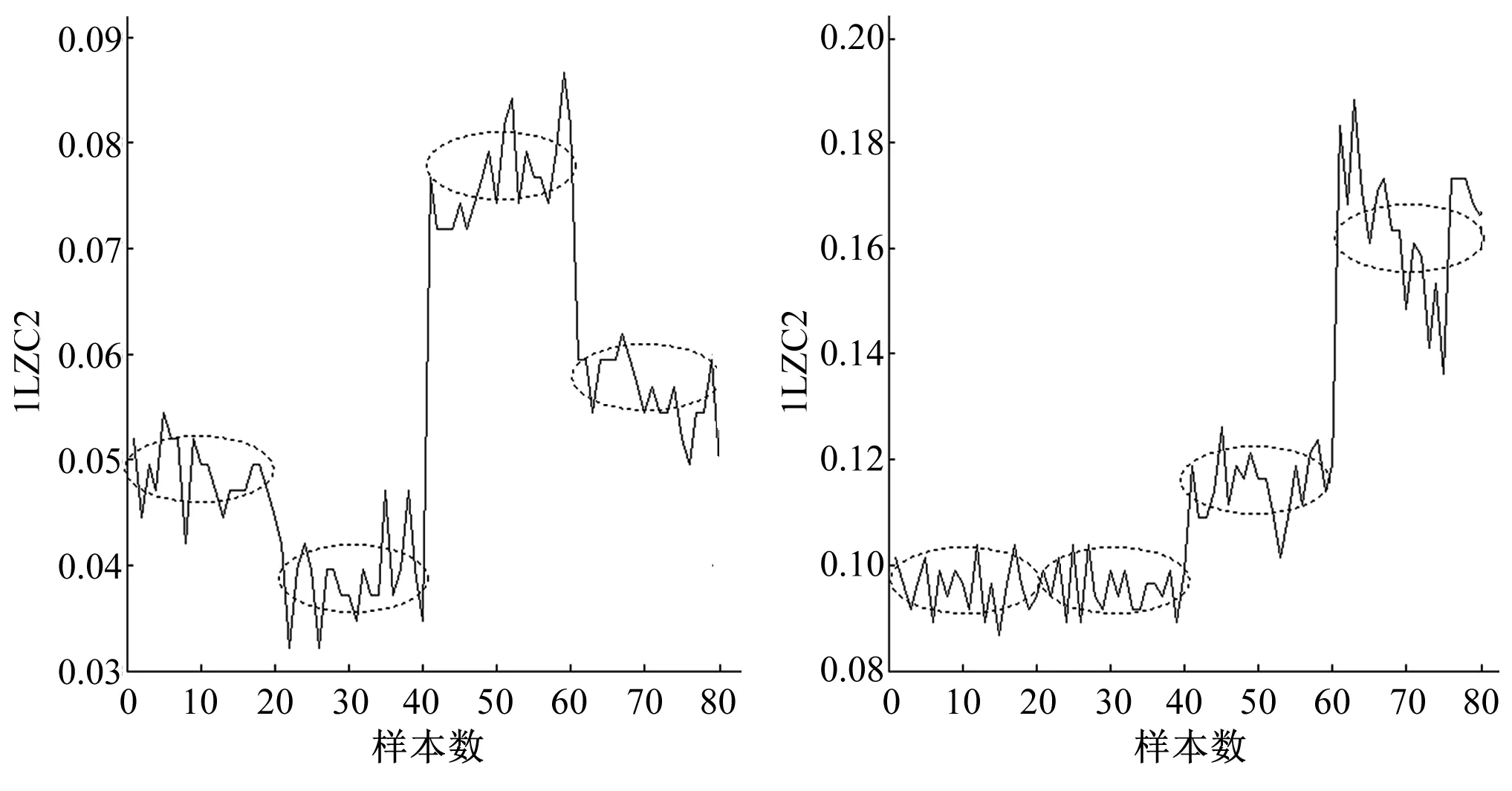
图3 各模态分量的复杂度特征集Fig.3 Complexity feature set of each modal component

从图3中可以看出，第一个模态分量的复杂度特征值，对4种运行状态具有较好的区分度；第二个模态分量的复杂度特征值，对前两种运行状态区分不明显，但对后两种运行状态区分较明显。

分别取各运行状态下振动信号的10组作为训练样本，10组作为测试样本，并采用VMD分解，提取前两个IMF分量计算其复杂度值。不同运行状态下振动信号各模态分量的复杂度特征指标如表2所示。

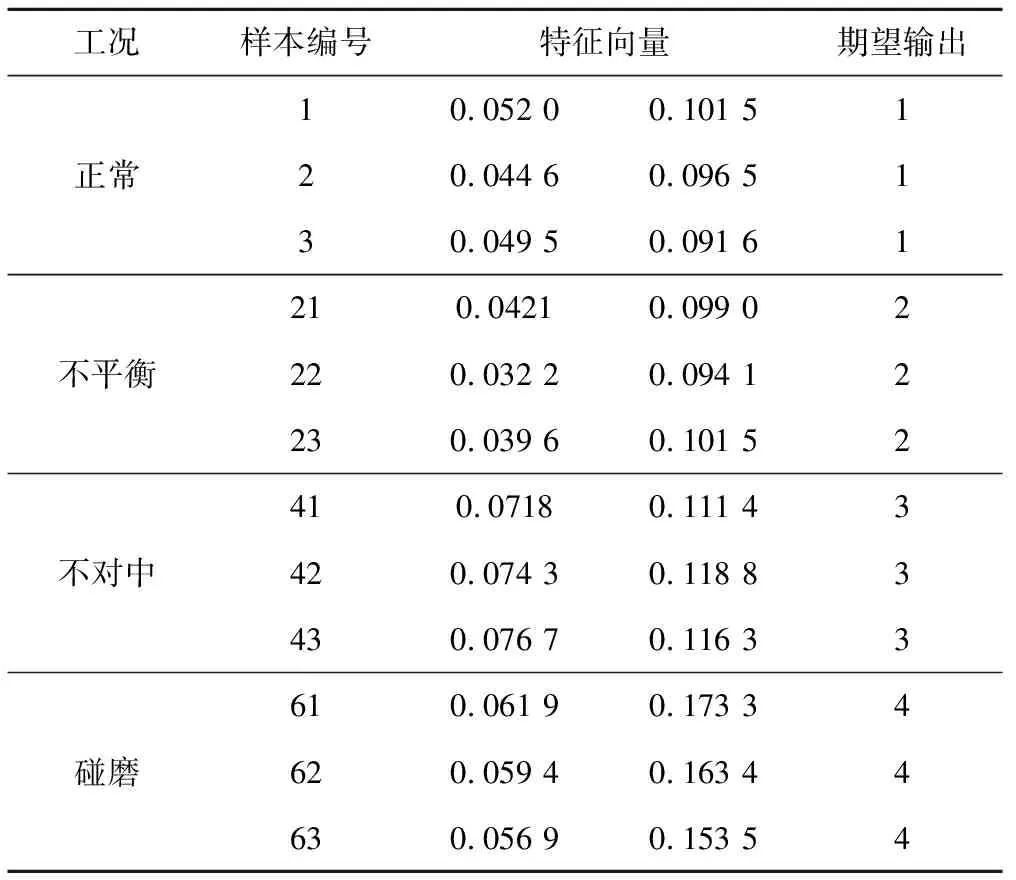
表2 不同工况下振动信号经VMD分解后的复杂度特征向量表Tab.2 Complexity feature vector table after vibration signal decomposition by VMD under different working conditions

将上述特征向量集输入到支持向量机分类器中进行识别，SVM核函数选择高斯核函数，并采用一对一进行多类识别。图4为测试样本的分类结果，表3为不同运行状态的辨识结果。

图4 测试样本集数据分类结果图

表3 不同工况辨识结果%Tab.3 Identification results of different working conditions

从图4可以看出，SVM分类器实际输出的分类结果与预测输出结果非常接近。由表3可知，采用SVM分类器得到的故障识别率最高为100%，平均识别率达到92.5%，表明基于变分模态分解和复杂度分析相结合的方法的能够较为准确地提取出振动信号特征。

2.2 水电机组实测信号特征提取与分析

现有某水轮发电机组在运行过程中出现强烈振动，经专业人员检测后发现机组出现水力因素不平衡故障。采集该机组故障前，故障中和故障后3种运行状态的振动信号，利用本文提出的方法对该机组的3种不同状态进行信号特征提取与分析。该机组额定转速为107.1 r/min，采样频率为1 000 Hz，对三种工况各采集40组数据，每组数据长度均为4 096，训练样本数与测试样本数均为20。对故障前的振动信号采用小波阈值降噪并进行VMD分解，结果如图5和图6所示。

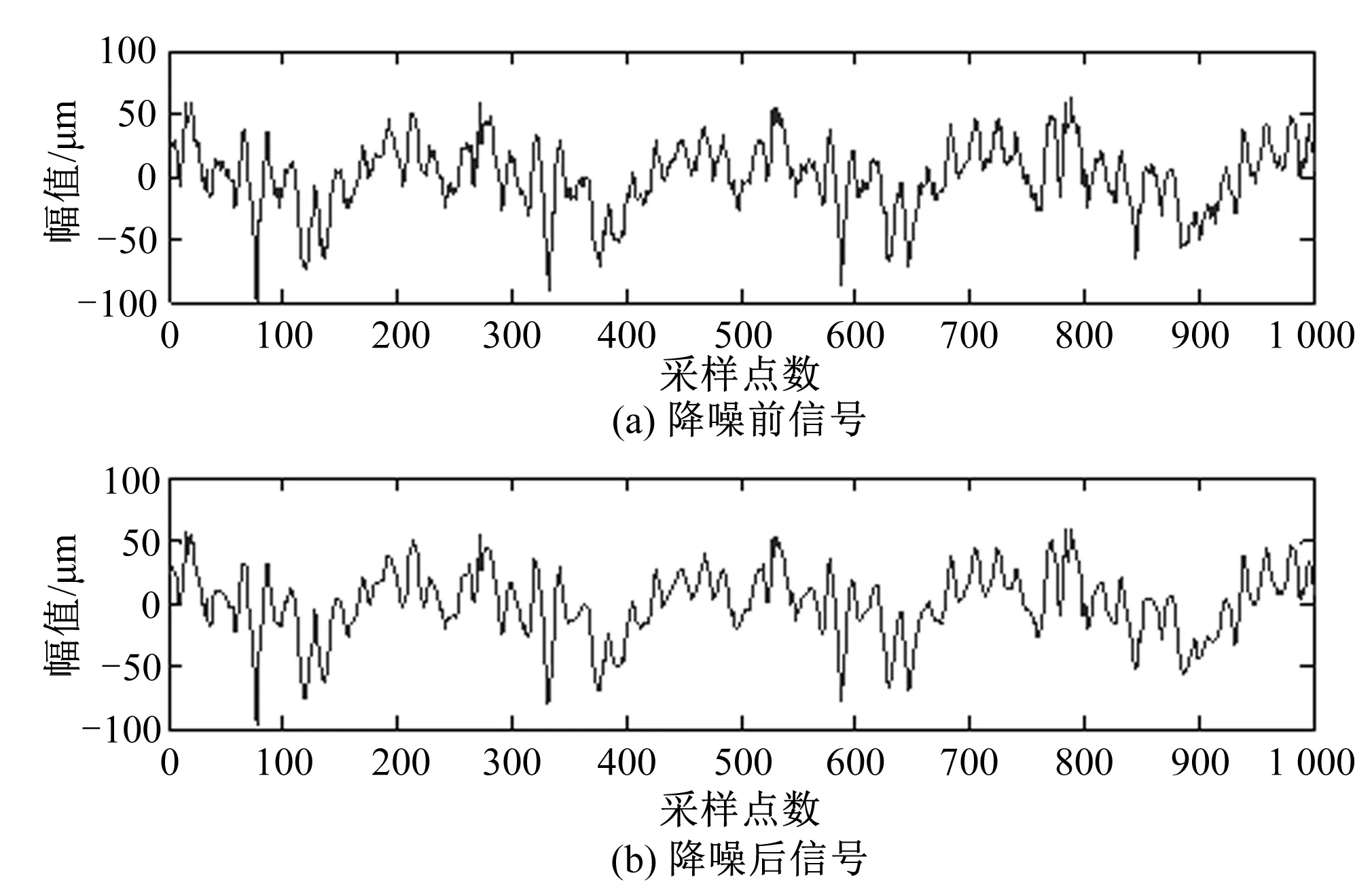
图5 采用小波改进阈值降噪后波形图Fig.5 Waveform diagram after wavelet reduction with improved threshold reduction

图6 故障前振动信号(K=3)变分模态分解图Fig.6 Variational mode decomposition diagram of vibration signal (K=3) before failure

对不同运行状态的振动信号进行VMD分解后，根据相关系数确定最佳分解个数为K=2，并将前2个模态分量的复杂度值作为特征向量，不同运行状态下振动信号各模态分量的复杂度特征指标如表4所示。

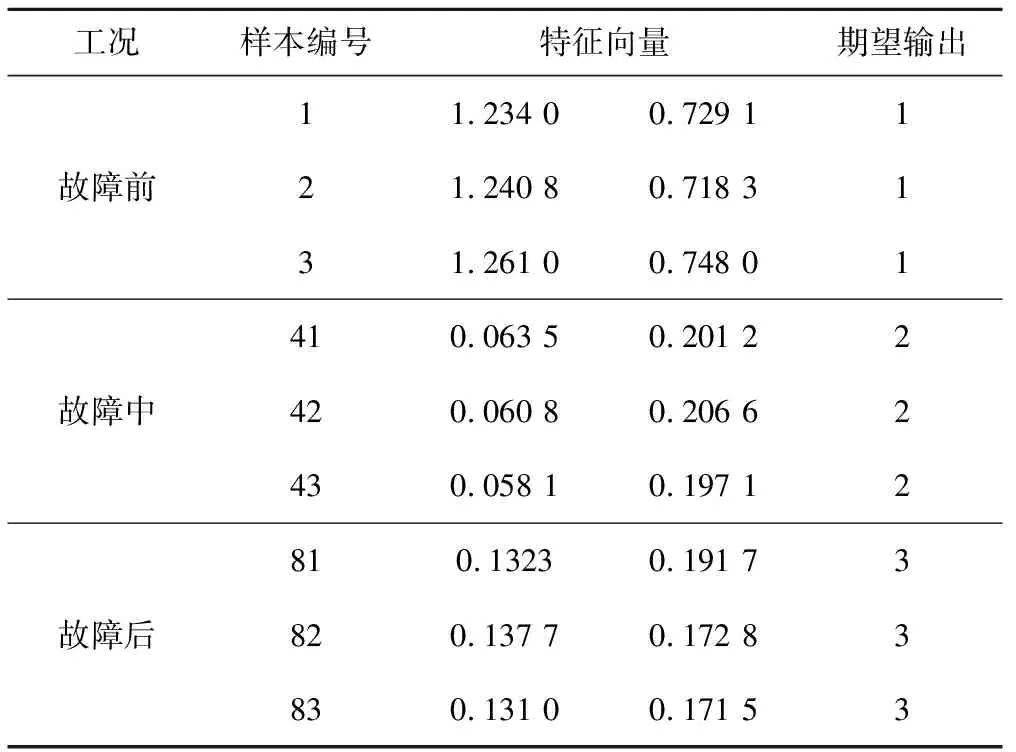
表4 不同工况下振动信号经VMD分解后的复杂度特征向量表Tab.4 Complexity feature vector table of vibration signals after VMD decomposition under different working conditions

同样，将得到的特征向量集输入到支持向量机中进行分类识别，结果如图7和表5所示。

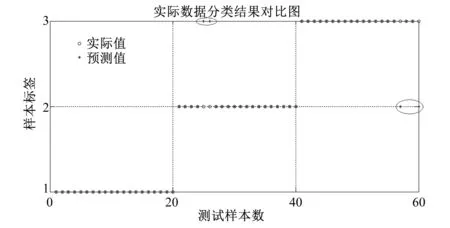
图7 测试样本集数据分类结果图Fig.7 Test sample set data classification result graph

从图7与表5可以看出，对于水电机组不同运行状态的平均识别率达到93.3%，表明基于变分模态分解和复杂度分析的方法是一种有效的水电机组振动信号特征提取方法。

表5 不同状态识别结果 %Tab.5 Different status recognition results

3 结 语

本文提出了基于变分模态分解与复杂度分析的水电机组振动信号特征提取新方法，并利用转子振动试验台模拟信号和水电机组实测信号来验证该方法的有效性和可靠性。结果表明，基于变分模态分解与复杂度分析的方法能够较为准确地提取出振动信号的特征，对水电机组故障诊断具有一定的参考价值。