涡旋电磁波产生原理与仿真实现

刘知房

（杭州第十四中学,浙江杭州，310000）

1 简介

自1992年由Allen等人用麦克斯韦方程组理论推导[1]，并在1994年由实验验证[2]之后便开始在学术界得到广泛的关注和深度研究。电磁波携带能量和动量，动量可分成线动量和角动量，角动量又可以分成自旋角动量和轨道角动量[3]。自旋角动量与电磁波的极化有关[4]，而轨道角动量表现为波前围绕电磁波传播方向所在的轴旋转，也称为“涡旋电磁波”。携带不同轨道角动量的电磁波的波前螺旋状态不同。电磁波自马可尼时代开始既已使用振幅作为信息传输手段[5]。其中，频率表示振幅变化的快慢而相位则表示振幅在什么时间变化，其用振幅作为信息载体的通信手段至今没有变化。电磁波的到底是什么，人们至今对其认识也只停留在马可尼时代。然而，轨道角动量，作为一种拓扑结构，给人们提供了一种新的视角去研究和开发电磁波。作为电磁波携带的一个特殊维度，电磁轨道角动量有很多潜在的应用。在通信方面，电磁波不同轨道角动量之间相互正交，通过复用不同的轨道角动量，并经由同一个口径发射或接收，可以极大提高通信容量。在导航方面，携带轨道角动量的电磁波的中心能量为零，而两侧存在能量峰值，其辐射图呈现倒锥状，且不同轨道角动量电磁波的波束角不同，可以将这些特性与角度等参数建立联系，构成新的测速测角方法。在探测方面，轨道角动量电磁波的波前呈现螺旋状，其探测的目标反射特性必定具有新的特性，可以加以研究以弥补常规雷达的缺点，而且可以利用轨道角动量电磁波进行雷达成像[6]。

本文将分别从数学建模、理论推导、仿真计算三个方面分别介绍两种产生方式，并利用电磁仿真软件对两种产生方法进行仿真计算，从而加深对两种产生方式的理解和运用。

2 数学原理

具有轨道角动量的电磁波场强可以表示为

其中，ρ表示柱面坐标的半径，z表示探测平面与发射源的垂直距离，ϕ表示柱面坐标的方位角。对于平面电磁波来说，在柱坐标纵轴z相同时其相位随方位角变化是恒定值，即 eiϕ为一个常数，不随矢径取向变化改变；而具有轨道角动量的电磁波，其相位随方位角而线性变化，此种电磁波即具有轨道角动量。

现有的OAM发射天线主要有两种产生方法：天线阵列和螺旋相位板。其结构分别如下图1中（a）和（b）所示。螺旋相位板等的缺陷在于其模式数由其实际形状决定，无法变化，只能固定接收一种模式数的电磁波，不方便使用。而阵列天线法，通过数字处理来对不同天线接收到的信号进行相移处理再经过合成后得到完整的信号，因此可以自由控制模式数，较之前的方法明显较优。

图1 OAM天线设计方式

根据天线理论，天线阵列的辐射场可以采用方向图乘积法得到，即：天线阵列总的辐射场等于阵列因子与单个阵子的辐射场的乘积得到。公式表示如下：

其中Etot表示总的电场辐射图，Ea表示单个阵子的电场强度辐射图，表示全项阵子组成的天线阵列产生的辐射图。该公式只在阵列中所有阵子都相同时成立。

为了简化，在计算中，采用点源代替真实天线尺寸参与阵列因子的计算。下面计算OAM天线的阵列因子。如图2所示，假定N个各向同性的阵子沿着半径为a的圆环等间距的分布在xOy平面上，则归一化方向图可以表示如下：

其中，Rn表示第n个阵子到观测点的直线距离，λ表示波长表示传播常量表示第n个阵子的激励系数，In和αn分别表示第n个阵子的幅度和相位，r表示圆环阵列的中心到观测点的直线距离。

图2 环形天线阵列结构

通常对于r≥a，上述的等式可以近似如下：

假定Rn≈r，我们有：

为了产生模式数为l的OAM电磁波，第n个阵子的激励相位应该具有如下关系：

因此，由式（6）可以推导如下：

式（8）即为第一类贝塞尔函数，因此可以表示成如下形式[7]：

式（9）即为圆环阵列产生OAM电磁波的天线阵列因子。

3 仿真计算

3.1 Matlab仿真

Matlab中主要是完成对环形天线阵列产生OAM电磁波的仿真。其环形阵列模型如第二节数学模型所示。假定，阵子个数为40、阵列半径为6λ、射频频点为35GHz、OAM模式数为1、接收距离为106λ、检测平面为60×60点，得到OAM=+1的电磁波相位和幅度分布图如图3所示。

由图3可以看出，OAM电磁波的能量分布中心存在能量空心，相位呈现螺旋状分布。因此，OAM电磁波的波束角会随着传输距离的增加而不断变大。

图3 OAM电磁波相位分布和幅度分布

基于式（9）的方向图函数，可以用Matlab对OAM参数进行仿真和优化，如图4所示。随着OAM模式数的增大，波束发散角增大；随着频率的增大，波束发散角减小，但是在阵列口径和天线阵子数量固定的情况下，旁瓣随着频率的增大而增大。

图4 不同模式和频率得到的方向图

3.2 CST仿真

3.2.1 线天线阵仿真

首先，在CST中构建半波振子模型，其直径为0.003λ、单边长度为0.5λ、间隔长度为0.025λ，其模型如图5所示。在此基础上，构建8阵子环形天线阵列。仿真频点为f = 25 GHz，阵列半径为R = λ。8个阵子的馈电依次延时45o。

图5 半波振子环形阵列仿真

由图5可知，线阵列很好的产生了OAM电磁波。但是，由于采用半波振子，旁瓣较大，且由于半波振子产生的是面包圈装的方向图，进而导致产生的OAM电磁波波束也是方向相反的两个波束。

3.2.2 平板天线阵仿真

平板天线阵子建模如图6所示。基于该平板天线，构建环形天线阵列，阵列口径为D = λ，阵子的馈电相位依次延迟45o，仿真频点为2.4 GHz。仿真得到的3D辐射图如图6所示。

由图可知，8平板阵子构建的环形阵列很好的产生了OAM电磁波。并且，由于平板阵子具有很好的定向性，从而产生的OAM波束也具有很好的定向性，旁瓣较小。

图6 平板天线阵仿真

为了分析阵列口径对OAM电磁波的影响，如图7所示仿真了天线口径D = 4λ时的阵列3D辐射图。随着阵列口径则增大，波束主瓣的张开角度减小，但是旁瓣增多。

图7 8阵子平板天线3D辐射图，阵列半径为D = 4λ

4 讨论与总结

以上仿真中，平板天线阵的馈电方式采用的是独立馈电，即：每个阵子单独馈电，各个馈电相位依次设定为延时45o。

3.2.3 螺旋相位板仿真

本节将仿真螺旋相位板产生OAM电磁波的方法。制作螺旋相位板的材料为高密度聚乙烯（HDPE，硬塑料），其中一个面是平面，另一个面呈螺旋状，其螺旋高度随方位角变化的计算公式为[8]：

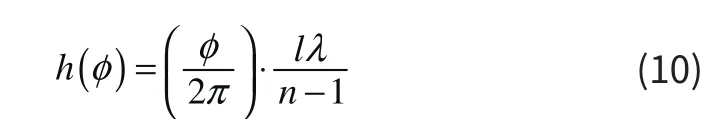
根据（10）式可以得到最大的螺旋高度差为：

电磁波轨道角动量提供了除幅度、频率、相位、极化之外的额外维度。具有不同OAM模式的电磁波可以复用传输，提高传输速率和频谱效率。通过天线阵产生OAM电磁波，操作方法简单，产生模式灵活可变。然而，由于OAM电磁波具有环形波束的特点，波束中心能量为零，所以现有可用的传输方式多为全空域接收方法，即：接收端将整个环形波束全部接收，通过与发射端相反的OAM模式的相位进行补偿恢复发射信号。这种传输方式会导致接收天线阵尺寸随着传输距离而增大，无法实现自由空间长距离传输。因此，目前OAM电磁波传输多应用于光纤通信，这是因为光纤对光具有全反射特性，可以束缚波束的发散。若能实现OAM电磁波在自由空间的长距离传输，特别是OAM电磁波的复用传输，则将极大提高频谱效率。

其中，φ为方位角（其变化范围为：0～2π），n表示螺旋相位板材料的折射率，λ为电磁波的波长。

根据上述计算公式在CST仿真软件中构建螺旋相位板模型如图8所示。同时为了仿真螺旋相位板的性能，建立了如图8所示的波纹喇叭天线。喇叭天线口径处放置螺旋相位板结构如图8所示。采用螺旋线相位板产生的OAM电磁波3D辐射图如图8所示。由图可见，产生的波束并不对称，这是由于采用CST进行电磁仿真时涉及到很多计算参数的调节以及网格计算的设置，特别是对螺旋相位板中间精细尺寸的仿真计算，所以仿真时，对于稀薄尺寸的地方应该采用较密集的网格提高精度，对于尺寸较大且比较规则的地方应该采用稀疏网格以减少计算量，具体设置还需根据仿真结果反复调节。

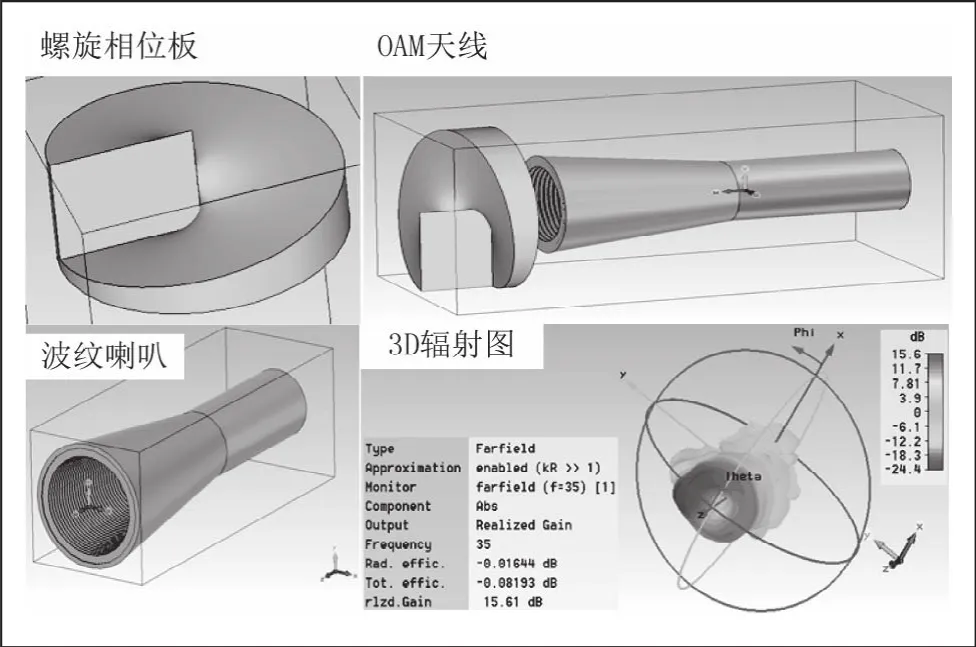
图8 螺旋相位板方式产生OAM电磁波