微振动对高分辨率TDICCD图像辐射质量影响
,,,
1.航天东方红卫星有限公司,北京 100094 2.北京空间机电研究所,北京 100094
遥感卫星高分辨率成像技术在近年来得到了长足的发展。随着图像分辨率的提高,在以前低分辨率条件下不重要的因素现在也会对图像质量产生很大影响。其中微振动是影响高空间分辨率遥感卫星成像质量的重要因素之一,振动的幅值、频率以及时间延迟积分电荷耦合器件(Time Delayed and Integration Charge-Coupled Device,TDICCD)的级数等因素都会对成像质量产生不同程度的影响。
微振动是指航天器在轨期间产生的一种幅值较低的颤振,其中诱发颤振的原因包括空间环境的干扰(如太阳风等),以及自身部件运作时产生的影响(如太阳翼、制冷机、动量轮等机构工作时造成的颤振)。在实际中,航天器颤振形式非常复杂,往往是由多个运动组合而成,在建模过程中,通常会将模型进行一定的简化,以便于研究和分析。目前,对微振动的影响的研究取得一定的进展。文献[1]应用集成建模的思想对高分辨率空间相机进行了微振动影响的结果光学集成分析;文献[2]研究表明TDICCD相机对卫星颤振幅值要求较高,且随TDI积分级数的增加,颤振的影响尤为突出;文献[3]从像移影响的角度进行了分析;文献[4]对面阵以及TDI推扫成像建立了颤振退化模型,并进行了仿真和验证;文献[5]在“973”子课题的支持下研究了平台颤振对高分辨率遥感影像质量的影响与补偿;文献[6]利用快速面阵CCD实现了振动参量的检测;文献[7]研究了低频正弦振动模型下的影响规律;文献[8-10]也都从不同角度分析和研究了平台振动对成像质量的影响;文献[11]分别就面阵、线阵推扫以及TDI推扫3种模式提出了相应的动态成像仿真模型。本文主要结合TDICCD相机成像过程和原理建立退化模型,并进行仿真,重点研究微振动对TDICCD图像辐射质量的影响规律,并针对微振动的不同影响因子包括微振动的振幅、频率和TDI级数分别进行了分析和研究,研究结果以期对工程实践有一定的指导意义。
1 仿真模型建立
1.1 模型建立
相机曝光成像的过程可以理解为探测器接受物面光强信息的一个积分过程,表达式如下:
(1)
式中:(x0,y0)为成像平面坐标;T为曝光时间,g(x0,y0)和f(x0,y0)分别为像函数和物函数。若目标与成像器件在曝光期间存在运动,那么这个曝光过程就变成:
(2)
式中:x(t),y(t)为运动函数。
TDICCD采用时间延迟积分和多级能量累加的方法来增大系统的灵敏度,具体的工作原理如图1所示。
TDICCD是一个面阵CCD,总共有N×n个像元,n代表垂直TDI方向上像元的个数,N代表级数,一般来说n远大于N,右侧为得到的m行n列的遥感图像。其中TDICCD采用推扫成像的方式,逐行输出。在推扫过程中,电荷在不同级CCD间进行转移和累加,并且使电荷转移速率与像扫描速率保持一致,使得不同级CCD对同一行景物成像得到的电荷能够累加在一起并输出,得到一行景物图像。同时通过推扫,可对地物进行逐行成像以及逐行输出,来得到右侧m行n列的遥感图像。
结合存在运动时的曝光成像规律和TDICCD的成像过程,可对微振动影响下的TDICCD的成像规律进行研究。经分析得,TDICCD的第k级对图像的第i行进行扫描积分成像的时间段为[(i+k-2)T,(i+k-1)T],由此可知此积分时间内对应的微振动大小情况,进而在积分过程中考虑微振动的影响。仿真过程为:

(3)
式中:T为一级CCD成像的曝光时间,即成像行周期,x(t)、y(t)为微振动影响函数。由式(3)可计算出微振动影响下的仿真退化图像。其中对于离散的数字图像,当采样点未落在原输入图像像素的中心位置上时,通过双线性插值的方法计算得到其对应的像素灰度值大小。对于每一个行周期T内的积分运算,采用辛普森积分法来进行计算:
(4)
式中:a、b分别为积分的上下限;f(x)为原积分函数;P(x)为数值积分中的插值多项式函数。
1.2 评价指标
文章重点针对辐射质量进行研究,其中通过对比度和清晰度指标来对图像辐射质量进行刻画。对比度和清晰度指标数值越大,表明图像越清晰,数值越小表明图像越模糊。其中对比度的计算如下:
(5)
式中:δ(i,j)为相邻像素间的灰度差;Pδ(i,j)为相邻像素间的灰度差为δ的像素分布概率,像素相邻按照四近邻的方式进行计算。
清晰度[12]计算如下:
(6)
式中:m、n分别为图像的行列数。Laplace邻域算子采用四邻域算子,即单像素点Laplace代数和为:
Ixy= 4f(x,y)-f(x-1,y)-f(x+1,y)-
f(x,y-1)-f(x,y+1)
(7)
2 仿真结果
2.1 仿真输入
根据第1节的仿真模型,采用Matlab平台进行模拟仿真,所用的清晰原图像为分辨率0.3 m的圣保罗商业区街道,大小为128×512,其中卫星和相机的参数如表1所示,微振动参数如表2所示,所得仿真结果如图2所示,图3为图2中图像圆圈处的局部放大。

表1 卫星和相机参数
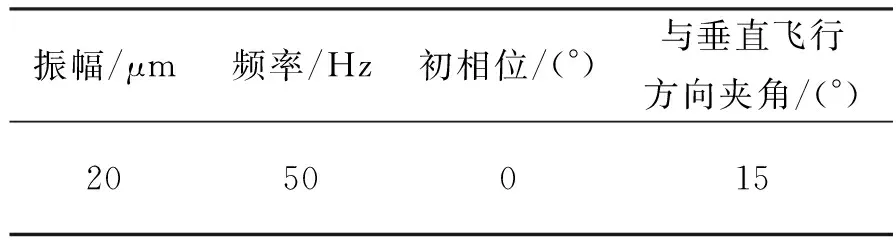
表2 微振动参数
由图2仿真结果以及图3的局部放大图中斑马线和网格线可以看出,得到的仿真退化图相比于原清晰图像既有图像模糊,也有几何的形变,这是由于TDICCD独特的成像方式所引起的,与理论分析结论一致。
其中原清晰图像的对比度大小为374.64,清晰度大小为1 803.2,仿真得到的退化图像对比度大小为233.31,清晰度大小为837.69。通过指标对比可得,微振动影响下的退化图像的清晰程度相比原图像下降,与理论分析一致。
由于TDICCD独特的成像方式,使得每一行像素的退化程度不同。图4给出了不同行的MTFA随行数的变化曲线,表3给出了其中第1行、第50行和第100行的x方向和y方向的奈奎斯特频率下的MTF值以及两个方向上的MTFA值。由表1、表2中参数计算可得,行周期T≈0.040 ms,微振动振动周期为(1/50) s=0.02 s,即500行图像约可覆盖一个振动周期。考虑到每行图像是由N=48级CCD叠加成像得到,不妨取中间的一级对应的相位作为每一行对应的相位来进行分析,由振动初相位为0便可计算得到第105行相位约为π/2,第480行相位约为0。由图4和表3可以看出,MTFA曲线随行数呈现出一定的规律,并且在0相位处MTFA值较小,图像退化比较严重,在π/2相位处MTFA值较大,退化较小。这是由于在0相位处运动的平均速度较大,在相同的积分时间内产生更大的像移,使得图像退化更为严重,所得结果与理论分析结果一致。
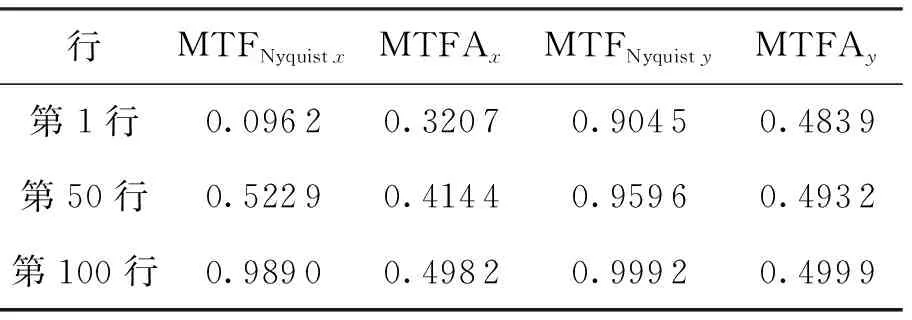
表3 不同行MTF相关参数
2.2 振幅影响分析
图5和图6分别为垂直运动方向和沿飞行方向微振动下,当振动频率、TDICCD级数等因素不变,只有振幅变化时的对比度和清晰度变化曲线。
从图5和图6可以看出,随着微振动振幅的增加,不管是垂直运动方向还是沿飞行运动方向,图像的对比度和清晰度在一些局部范围内因为图像像素相关性等原因会有波动,但总体的走势是一直下降的,即随着振幅的增加,图像退化程度更严重,这与理论分析和实际工程的结果是一致的。
2.3 频率影响分析
图7所示为垂直运动方向微振动下,TDICCD级数分别为16、48和64时,随着振动频率的增加,图像的对比度和清晰度的变化曲线。图8所示为沿运动方向微振动下的相应情况。
由图7可以看出,垂直运动方向微振动下,对于不同的级数N,随着频率的增加,图像的对比度和清晰度总体上都呈现下降的趋势,并且在低频时下降速度较快,高频时下降速度变缓。原因可结合图9进行分析。图9所示为TDICCD一个积分时间te、N级总的积分时间与微振动一个振动周期间的对比关系。随着频率的增加,振动的周期变短,TDICCD同样的积分时间内对应的振动位移就变大,引起的像移就变大,使得图像退化更为严重,因此曲线呈现下降趋势;同时,0相位处变化速率大于π/2相位处,频率增加时像移的增加速度变慢,因此曲线变化速率变缓,当振动频率增加到TDICCD总的积分时间能把最大振幅包含进去时,图像的退化程度几乎达到了最大,变化便不明显了。此外,对不同级数N情况下的变化曲线进行对比分析可以看出,级数比较大时图像退化更为严重。这是由于在一定范围内,级数越大,总的积分时间越长,对应的振动位移越大,像移越大,各级数成像叠加后图像越模糊,图像退化越严重。同时,在级数较小时,N=16处当频率较低时局部波动较另外两条曲线更大,这是由于级数较小时图像更多的是几何形变的影响,在图像模糊上影响不多,因此局部会有更多波动。
由图8分析可得,对于沿运动方向的微振动,同样的对于不同的级数N,随着频率的增加,图像的对比度和清晰度总体上都呈现下降的趋势,并且在低频时下降速度较快,高频时下降速度变缓。以及在一定范围内,级数越大,总的积分时间越长,像移越大,各级数成像叠加后图像越模糊,图像退化越严重。
此外,将两个方向的微振动结果进行比较可以看出,沿运动方向的微振动随着频率的增加,在局部上其波动相对更大一些,这主要是由于TDICCD独特的推扫成像方式,使得两个方向的微振动对图像的质量影响有一定的差异,沿飞行方向的振动得到的结果局部上有更多的波动。
2.4 TDI级数影响分析
图10所示为垂直运动方向微振动下,振动频率分别为50 Hz、100 Hz和200 Hz时,随着TDICCD级数的增加,图像的对比度和清晰度的变化曲线。图11所示为沿运动方向微振动下的相应情况。
由图10可以看出,在垂直运动方向微振动下,在一定TDICCD级数范围内,随着级数N的增加,图像的对比度和清晰度都呈下降趋势。在较高频率时其下降速度随着级数的增加越来越缓,在200 Hz时略微有一些反向上升的趋势。结合图9进行分析,在一定范围内,随着级数的增加,总积分时间内对应的振动位移变大,像移变大,图像退化更严重,当级数很大使得其包含最大振幅时,图像退化程度几乎达到最大,曲线下降趋势变缓,甚至有一些反向上升的趋势。此外,不同频率的曲线之间比较可以看出,一定范围内的级数下,频率较高时其对比度和清晰度更低,图像退化更为严重,这与上一小节中的结论相一致。
由图11分析可得,对于沿运动方向的微振动,在一定TDICCD级数范围内,随着级数N的增加,图像的对比度和清晰度在低频时基本呈下降趋势,在高频时先下降后反向上升,并且频率越高极值点对应的级数越小。此外,不同频率的曲线间比较可以看出,在级数较小时,频率越高,其退化越严重,当级数较大时,退化程度随频率呈现一定的波动。从上面的分析和结果也可以看出,垂直运动方向的微振动和沿飞行方向微振动对图像的影响规律不相同,有一定的差异,这主要和TDICCD独特的推扫成像方式有关,与上一小节分析一致。
2.5 相位影响分析
由于TDICCD独特的推扫成像方式,使得退化图像的不同行对应的成像时段不同,导致其对应的相位不同,使得不同行的退化程度不同,在第2.1节中有一定的阐述。
此外,当初相位发生改变时,对于退化图像的某一行而言,其对应的振动相位发生改变,该行图像的退化程度会有所改变。但对于整幅图像而言,当行数较多可以覆盖振动的一个周期时,从整幅图像的角度来看,图像质量没有多少变化。
3 结束语
本文主要研究了微振动对TDICCD相机图像的辐射质量的影响规律。通过建立成像模型,并进行仿真计算,得到仿真退化图像。以及针对微振动的不同影响因子进行了分析,所得结果与理论分析或者工程实际情况基本一致。主要包括以下几点:
1)由于推扫成像方式,不同行退化程度不一致;
2)振幅增加,其他因子不变,图像辐射质量整体呈下降趋势;
3)频率增加,其他因子不变,图像辐射质量整体呈下降趋势,下降速率越来越慢;
4)TDI级数增加,其他因子不变,图像辐射质量整体呈下降趋势,下降速率越来越慢。
随着卫星分辨率的不断提高,微振动影响越来越明显。结合相关研究,提出以下几点关于如何减小微振动的影响的建议,以期对工程实践提供参考。
1)在卫星设计阶段就要系统地考虑微振动的减振隔振问题,对扰振源的频率进行特定的设计;
2)对相机等敏感载荷进行特定设计,在微振动传递路径上使用特殊材料,减小传递到载荷处的振动量;
3)从后端图像处理的角度分析微振动的影响规律,采用图像复原算法对图像进行恢复处理,提高图像质量。

