星间测量自主导航改进状态相关黎卡提方程滤波
,
中国空间技术研究院 钱学森空间技术实验室,北京 100094
分布式卫星系统是由物理上互不相连、共同协作完成同一航天任务的多卫星构成的空间系统[1],由于其具有对地面依赖性小、自主性强、灵活可变、综合成本低等特点,成为卫星技术发展的新趋势。分布式卫星系统实现自主协同需具备的核心和基础能力是自主导航[2],其自主导航问题与普通卫星存在较大区别:既需要确定每个卫星的精确空间位置和速度,又需要确定卫星之间的相对位置速度关系。在分布式卫星系统应用任务中,卫星间的相对信息相对于绝对信息更容易获得,近年来,利用星间相对观测的自主导航技术备受关注。这些相对观测量包括视线角、星间相对距离和相对位置矢量等[3-9]。能否基于相对测量序列求解各自卫星的绝对位置和速度,在理论上取决于系统的能观性能,在应用上涉及高性能定轨滤波算法。
文献[10-11]研究了基于星间测距的双星自主导航方法,指出没有先验信息,仅依靠相对距离测量的导航系统是亏秩的,并给出了严格的数学证明。文献[12]针对双星编队首次提出了仅利用地心惯性坐标系中星间相对位置矢量序列作为观测量的自主绝对导航方法,并采用局部线性化的方法分析了其能观性,文章指出此方法在半长轴相等的共面圆轨道情况下不适用,但未给出严格的理论证明。文献[13]对文献[12]提出的导航方法进行了物理角度的阐述,把双星系统视作一个巨型加速度计,并对定轨精度进行了分析,并说明该方法除几个0°倾角的特殊轨道外,在大部分情况下是能观的。文献[14]首次对基于星间位置矢量测量的双星自主导航系统使用非线性系统局部能观性理论进行分析,通过数学证明指出在两卫星瞬时地心距不相等的情况下可以定轨。文献[2]在上述研究基础上提出了非线性系统局部k阶能观性的概念,并证明了理想二体轨道模型下该自主导航系统局部4~6阶能观的充要条件及其与非线性系统能观性秩条件成立的关系。文献[15]考虑能观性强弱对滤波算法的影响,给出了一个基于相对位置矢量自主导航系统能观性秩条件的能观度指标,并据此对无迹滤波(Unscented Kalman Filter,UKF)算法进行改进,提高了导航定位的精度。但由于在算法中,指标只能基于位置速度的估计值而非其真值得到,因此不能真实反映系统能观度的大小。
卫星动力学模型是个典型的非线性系统,一般采用非线性滤波算法对轨道进行估计。常用的方法有扩展卡尔曼滤波[16-19](Extended Kalman Filter,EKF)和无迹滤波[20-22]等。状态相关黎卡提方程(State-Dependent Riccati Equation,SDRE)方法[23]通过构造线性结构解决非线性系统的最优控制问题,随之应用于非线性系统的估计[24],构成的滤波器被称为状态相关黎卡提方程滤波(State-Dependent Riccati Equation Filter,SDREF)。在无随机游走的确定性系统中,SDREF可以全部获得系统的非线性信息。这使得可以将非线性系统作为线性系统来处理,不存在线性化误差,且无需计算Jacobian矩阵。
在本文的研究中,SDREF被用作利用地心惯性坐标系中星间相对位置矢量序列作为观测量的自主导航估计器,并与EKF算法在滤波步骤、计算负担和滤波精度等方面进行了比较。本文推导并定义了一种新的在线反映能观性程度的特征量,提出了基于该特征量对滤波增益阵进行在线调整的改进SDREF算法。数学仿真表明,该改进SDREF算法在保持SDREF计算量小的优点下,导航估计精度明显优于采用EKF和SDREF算法的结果。
1 SDREF原理
SDREF是一种参数化的滤波方法,它将非线性系统改写为线性化结构,系统矩阵和观测矩阵的参数由当前状态决定,称为状态相关系数(State-Dependent Coefficients,SDC)。SDREF与EKF唯一的不同之处在于EKF是在估计状态附近展开进行线性化近似,而SDREF是将非线性系统做参数化处理,这一转换过程称为伪线性化。
考虑如下的连续非线性系统:
(1)
式中:X为n维状态向量;Y为m维观测向量;f(·),h(·)分别为n维和m维非线性函数;w和v分别为n维和m维高斯白噪声向量,各分量间互不相关,且满足
(2)
由文献[25]可知,如果f(·),h(·)可微且满足f(0)=0,h(0)=0,则非线性系统(1)可以转化为如下具有SDC的线性形式:
(3)
其状态方程和观测方程的系数矩阵以状态向量为参数。由于没有进行线性化近似,式(1)转化为式(3)的过程中不会损失任何信息,可以运用线性系统标准Kalman滤波方法对式(3)进行处理。
首先对式(3)进行离散化,得到
(4)
式中:Φ(Xk)为状态转移矩阵;H(Xk)为观测矩阵;wk和vk分别为离散化的状态噪声和观测噪声,当采样间隔Δt较小时满足
状态转移矩阵Φ(Xk)如下:
(5)
在计算时一般取二阶近似:
(6)
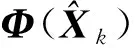
步骤1:选定滤波初值
步骤2:状态一步预测
(7)
步骤3:计算一步预测均方误差
(8)
步骤4:计算滤波增益
(9)
步骤5:计算估计均方误差
Pk+1=(I-Kk+1Hk+1)Pk+1/k
(10)
步骤6:状态更新
(11)
从上述过程中可以看出,与EKF算法相比,虽然SDREF没有线性化损失信息量,但是f(X)和h(X)在改写时拆解出了一个右乘状态向量,其对状态方程和观测方程的描述有所欠缺。因此SDREF和EKF两种算法对模型的近似程度高低难以给出明确的定论,后文会通过理论分析和数值仿真对SDREF和EKF算法在相对位置矢量测量自主导航系统中的表现进行探讨。
2 系统模型
考虑基于星间相对位置矢量测量的双星自主导航系统,将两颗卫星记为卫星A和卫星B,测量关系如图1所示。
O是地球中心,rA和rB分别是地心到两卫星的矢量,rAB是卫星A到卫星B的位置矢量。已知卫星A搭载了星敏感器和星间相对测量设备(包括无线电或激光测距仪、光学或雷达测向仪),可以测量自身在惯性空间中的姿态、卫星A与卫星B间的距离以及卫星B在卫星A本体坐标系中的方位,通过坐标转换可以得到两卫星在惯性空间中的相对位置矢量。
本文选取地心赤道惯性坐标系为参考坐标系,坐标原点为地球质心,基准面为赤道面,X轴指向春分点,Z轴指向北极,Y轴与X轴和Z轴构成右手直角坐标系。含J2摄动项的卫星轨道动力学模型为[26]:
(12)
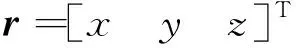
(13)
选取地心赤道惯性坐标系下两卫星的位置速度向量为系统状态变量,记
X为12维状态变量,则带J2摄动项的系统状态方程为:
(14)
其中系统噪声w包括未考虑的高阶地球非球形引力、太阳光压、大气阻力等摄动力。
观测方程为:
Y=h(X)+v=rA-rB+v=HX+v
(15)
3 SDREF与EKF计算量对比
在基于相对位置矢量观测的双星导航系统中,由于观测矩阵是线性定常的,SDREF与EKF唯一的区别在状态转移矩阵Φk的计算上,前者由当前时刻的参数化矩阵求得,而后者由Jacobian矩阵求得。
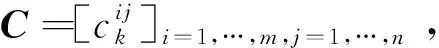
对于SDREF,状态方程(14)可以改写为:
(16)
记I3×3为I3,则离散后的状态转移矩阵为
(17)
对于EKF,状态方程非线性函数的Jacobian矩阵
(18)
式中:
状态转移矩阵
(19)
分析式(17)中SDREF状态转移矩阵的形式,可以得到以下定理。
定理1 在以式(14)为系统方程、式(15)为观测方程的导航系统中,若SDREF满足以下条件:
1)初始时刻估计向量协方差矩阵P0为对角4×4分块阵;
2)观测矩阵H为对角1×4分块阵;
3)状态误差和观测误差为各分量互不相关的白噪声,即Qk与Rk为对角阵。
则后续每一时刻的状态误差协方差矩阵Pk都是对角4×4分块阵。
证明:用数学归纳法进行证明。
1)当k=1时,显然成立。
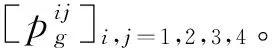
一步预测均方误差阵Pg+1/g为:
(20)
Pg+1/g是对角4×4的分块阵。
(21)
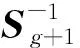
则滤波增益矩阵Kg+1为:
(22)
Kg+1是对角4×1分块阵。
将式(20)和式(22)带入式(10)中,由于Kg+1,Hg+1和Rg+1都是对角分块阵,所以Pg+1是对角4×4分块阵。
由式(1)(2),如果SDREF满足定理1的条件1)~3),则每一时刻的误差协方差矩阵Pk都是对角4×4分块阵。
在本文分析的自主导航系统中,定理1的条件是比较容易满足的,此时Pk,Φk,Kk均为对角分块阵,12维矩阵运算可简化为4维矩阵运算,计算量约是EKF的12.5%。
4 基于能观度的改进滤波算法
能观度是系统能观性强弱的度量,表征了系统状态可由输出反映的程度。非线性系统能观度的大小会随着状态变化而波动,从而对滤波算法产生影响。在能观度较大的时刻,系统由观测反映状态的能力较强,滤波估计误差较小;反之,能观度较小的时刻,由观测反映状态的能力较弱,滤波估计误差较大。
目前常用的能观度评价准则有基于能观性矩阵的评价准则和基于滤波误差协方差阵P的评价准则。基于能观性矩阵的评价准则需要计算矩阵的奇异值,求解比较繁琐,且要基于状态真值进行计算。由于在实际滤波中真值是未知的,因此这种评价标准并不能准确反映系统能观度的大小。基于滤波误差协方差阵P的评价准则不需要求解能观性矩阵,计算量比较小,但是在非线性滤波算法中,P阵不能反映真实的估计误差协方差大小,所以此准则也不能真实反映系统能观度的情况。
本文从能观度的物理意义出发,基于滤波算法量测更新过程给出了非线性系统能观度的另外一种表征方式。
(23)
矩阵的Frobenius范数定义为:若A=(aij)∈Rm×n,规定
(24)
已知Frobenius范数具有如下性质:
式中:λi(ATA)为矩阵ATA的第i个特征值。

依据以上分析,在滤波的时间更新过程中对一步预测估计误差协方差阵的计算公式进行修改,引入一个缩放参数ρ,将式(8)改写为:
(25)
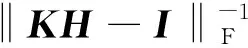
由此,依据当前时刻系统能观度的大小对误差协方差阵进行了修正,在适当扩大P的基础上兼顾到能观度的影响,增强了滤波的稳定性,提高了滤波精度。由式(7)、式(9)~式(11)、式(25)构成的算法本文称之为改进的状态相关黎卡提方程滤波算法(Modified State-Dependent Riccati Equation Filter, MSDREF)。

5 仿真与分析
考虑分布式卫星系统在卫星编队飞行、自主空间在轨服务和非合作目标测量等应用场景中,星间相对距离较近,因此选取两个轨道相近的卫星。两卫星的初始轨道参数如表1所示。
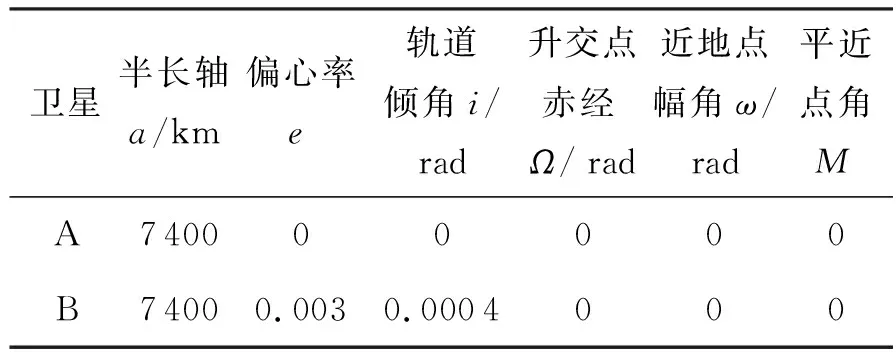
表1 两卫星初始轨道参数
卫星A搭载了星敏感器和星间相对测量设备(包括无线电或激光测距仪、光学或雷达测向仪),可以测量自身在惯性空间中的姿态、卫星A与卫星B间的距离以及卫星B在卫星A本体坐标系中的方位。利用上述测量量,相对位置矢量在惯性空间中的坐标可由下式解得:
(26)
仿真时间为40 000 s,星敏感器观测数据更新率为0.5 Hz,星间测距数据采样率为0.2 Hz,设定滤波周期为10 s,在同样的初始条件下分别用EKF、SDREF和MSDREF算法对基于星间相对位置矢量测量的自主导航系统进行仿真,MSDREF的参数γ取0.3。

定义位置误差和速度误差分别为:
将本算例中自主导航系统在3种算法下的估计结果进行对比,如表2所示。可以看出EKF的计算时间约是SDREF和MSDREF的7~8倍,这与前述对3种算法计算量的分析吻合。在稳态误差方面,SDREF由于轨道模型非线性程度不高且不存在线性化误差,其估计精度与EKF基本相当;而MSDREF根据系统能观度的变化对滤波协方差阵进行在线调整,改善了EKF和SDREF对能观度敏感的问题,位置和速度估计的稳态误差是EKF的21%。
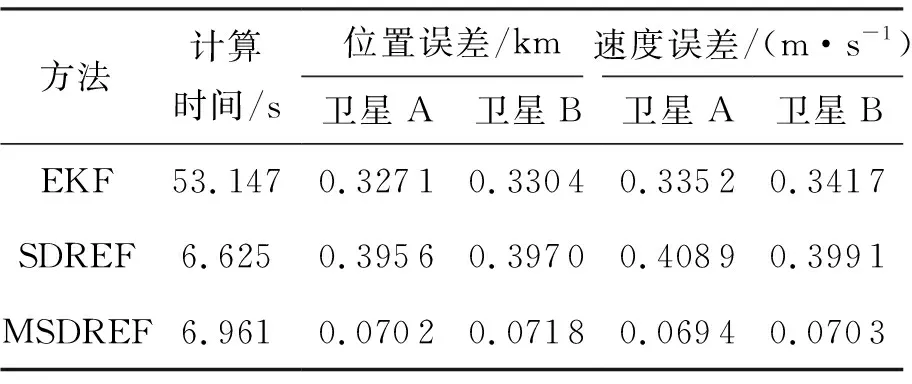
表2 EKF、SDREF和MSDREF估计结果对比
6 结束语
本文针对分布式卫星系统高精度自主导航的任务需求,选取典型的基于星间相对位置观测的双星模型,采用SDREF算法对自主导航系统进行估计,通过数学证明了在满足一定条件时,SDREF的计算量显著小于EKF的结论。文章提出了一种改进的SDREF算法,根据系统能观度强弱对标准SDREF算法进行在线修正,并选取一组近距离双星编队任务进行数学仿真,对EKF、SDREF和MSDREF的估计结果进行了对比。在相同条件下,MSDREF的估计精度明显优于SDREF和EKF,且保持了SDREF计算量小的优点。本文研究结果可以为未来分布式卫星工程实施中高精度自主导航算法的设计提供重要参考。

