复杂电磁环境中无源干扰对舰载雷达效能的影响研究
程占昕,闫仲钰
(1.海军大连舰艇学院,辽宁 大连 116018;2.北部战区海军联合海情预警中心,山东 青岛 266001)
0 引 言
现代海战是在复杂电磁环境下的信息体系的对抗,雷达作为水面舰艇信息获取的主要手段,如何在复杂电磁环境下充分发挥其应有的作战效能,是一个迫切需要研究和探讨的课题。复杂电磁环境的显著特点是电磁信号特性复杂、电磁信号密度高、电磁信号干扰强度大、电磁信号危害大。复杂电磁环境的干扰包含有源和无源干扰信号,而无源干扰信号是始终存在的。因此,深入探讨复杂电磁环境中无源干扰对舰载雷达使用效能的影响,对于充分发挥舰载雷达的作战效能具有重要的意义[1]。
本文主要研究敌方释放的无源干扰,特别是敌方干扰飞机。在飞机对水面舰艇攻击的过程中,无源干扰通常在伴随掩护攻击机群的情况下施放,距离舰船60 km左右,高度3 km左右,布放长度为10~60 km的无源干扰云带。在干扰弹投放后的最初10 min内,无源干扰反射器的分散情况,相对投放点在水平面和垂直面上均应服从高斯分布定律[2-3]。
1 无源干扰特性分析
1.1 无源干扰的密度
理想状态下,若在布放的立体空间中有70%的具有一定密度的反射器,则单架飞机在垂直于进攻方向上可形成一个椭圆形干扰区,该飞机施放的偶极子反射云的体密度[1]为:
(1)
式中:Q为偶极子反射器满载重量;q为每束偶极子反射器重量;Ldo为飞机的飞行距离;Nn为每束中偶极子的数量;α为利用系数;αx、αy为垂直于飞行方向的平面内偶极子散射的均方差值。
为方便起见,我们可利用无源干扰的线性密度,即:
(束/100m)
(2)
偶极子反射器的下降速度决定了偶极子反射器在空中的驻留时间,通常情况下为6~10 m/s,因此在正常大气压下,其驻留时间一般为数十分钟到数小时不等。
1.2 标准相关函数
在实际中,由于复杂因素的影响,所反射的舰载雷达信号会产生起伏,这些因素包括:
(1) 每个偶极子反射器的随机漂移;
(2) 雷达天线转动或舰艇航行;
(3) 舰载雷达工作频率变化。
偶极子反射体反射的信号瞬时值的概率密度分布规律应满足高斯定律。因此来自偶极子反射体反射的信号,其标准相关函数可用下式计算:
(3)
式中:k0i(τ)为引起信号起伏的第i个因素的信号标准相关函数;m为引起信号起伏因素总的个数。
由偶极子反射器随机漂移的所引起的相关函数为:
(4)
式中:v0为反射器运动速度的均方差值;λ为舰载雷达信号波长。
理论上精确计算k01(τ)是比较困难的,这里给出其标准相关谱值,如表1所示。
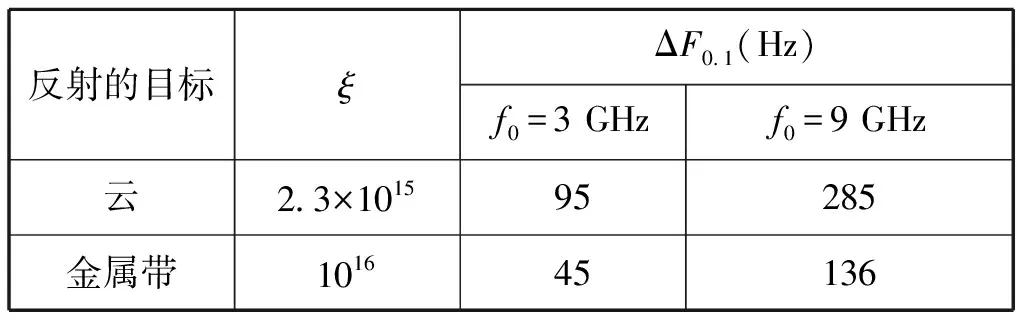
表1 标准相关谱
随着舰载雷达天线的转动,雷达波束在空间范围内扫描会发生变化,同样拓宽起伏信号的相关谱会引起反射信号的非相关。因此,体分布目标信号的标准相关函数可用下式计算:
(5)
式中:ωβ为舰载雷达天线旋转角速度;Δβ为舰载雷达天线水平波束宽度。
同时,舰载雷达航行时也会引起反射信号相位的变化和反射信号的起伏,因此体分布目标信号的标准相关函数可用下式计算:
(6)
其中:
(7)
式中:vα为舰艇的航速;β0为舰艇航向与天线波束指向之间的夹角。
舰载雷达的工作频率的改变也会引起起伏,这是因为信号相位是变化的。频率变化Δf的信号之间的相关函数K04如图1所示。

图1 振荡频率变化引起的相关函数
由图1可以看出,K04=0.2时的相关带为0.7τnΔf。综合考虑上述因素,可以得出无源干扰相关函数为:
K0(τ)=K01(τ)K02(τ)K03(τ)K04
(8)
2 无源干扰对舰载雷达效能的影响
2.1 舰载雷达发现效能概率
表征舰载雷达效能的指标有很多,这里采用发现效能概率来表示[2-3],即:
(9)
Φ(x)函数为:
(10)
2.2 无源干扰的功率
舰载雷达接收分系统能够接收到的无源干扰平均功率可用下式计算:
(11)
式中:ph为雷达发射机脉冲功率;λ为雷达工作波长;R为目标距离;G(β,ε)为舰载雷达天线增益;η为舰载雷达指定空域内体分布目标的有效散射面积;knn为干扰功率在空间、波导等所有传播路径上的衰减因子;v为场衰减乘积系数。
其中,无源干扰带的有效雷达横截面积(RCS)可用下式计算:
η=η0vp
(12)
式中:vp为舰载雷达照射空域的体积,如图2所示。
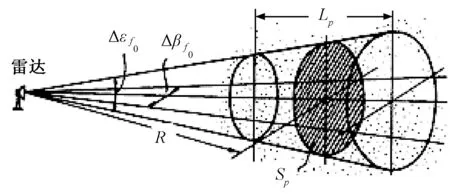
图2 舰载雷达波束覆盖的空域
根据图2,可以求出:
vp=LpSp
(13)
且有:
(14)
(15)
式中:Δβf0为电平为f0的水平波束宽度;Δεf0为电平为f0的垂直波束宽度;τn为舰载雷达脉冲宽度;c为光速。
依据式(12)~(15)可以获得:
(16)
此外,对于对称天线波束来讲,其增益为:
(17)
将式(16)和(17)代入式(11),便可获得舰载雷达接收机输入端无源干扰平均功率,即:
(18)
2.3 无源干扰下的雷达发现效能概率
由式(18)可以看出,无源干扰功率与雷达作用距离的4次方成反比,利用式(18)即可获得无源干扰条件下舰载雷达的发现距离:
(19)
3 结束语
本文在理论上给出了复杂电磁环境中无源干扰对雷达效能的影响模型,从模型中可以看出,无源干扰所反映的功率越大,则雷达发现效能概率就越低;无源干扰的起伏越复杂,则雷达发现效能就越差。当然,为了进一步定量分析其影响程度,还可作进一步的仿真计算。

