网络合成服务中的供应商竞争定价模型

陈思静，刘 峥，3，徐 琪

(1. 上海工程技术大学 管理学院，上海 201620；2. 东华大学 旭日工商管理学院，上海 200051；3. 上海交通大学 安泰经济与管理学院，上海 200030)

在网络服务市场领域，原子服务(即不能分得更小的服务)已不能满足消费者越来越多样化的网络服务需求，因而出现了基于组件的网络合成服务。网络合成服务能够将电子市场中的原子服务按照一定的规则合成新的服务，从而提供新功能的服务，其作为实现电子市场功能性需求的强有力途径，引起了广泛的关注[1]。网络服务技术建立在SOA(service-oriented architecture)架构和用于定向服务计算的解决方案基础上，其有3个参与者：服务提供商、服务注册中心和服务消费者。服务提供商以标准模式开发并发布网络服务。服务注册中心涵盖包括服务提供者地址、服务技术等在内的信息。服务消费者使用注册中心提供的信息，发现、组合并调用网络服务。

为了满足更复杂的功能性需求，网络软件设计者可以灵活地将不同服务组合为合成服务。这一组合基于单组件服务提供的功能，并以价值加成的方式将之改造成高等级的合成服务[2]，这一过程被称作网络服务组合。通过实施网络服务组合，网络软件设计者可以建立可执行的商业过程，包括商业逻辑和任务执行顺序[3]。网络合成服务定价研究具有重要的意义，其关乎网络服务的普及和服务提供商的经济收益。在当前电子服务市场中，网络合成服务的研究能够指导服务提供商，针对其提供的复杂的网络合成服务进行持续有效定价，从而获得最大化收益。然而，目前的相关研究主要集中在对原子服务的供应商定价问题策略指导和对合成服务进行科学有效定价的可行性验证等方面。文献[4]针对网络服务市场的破坏性创新研究指出，网络服务市场中的原子服务和合成服务的定价会影响该市场的服务创新和市场秩序。文献[5]认为，网络服务供应商应该考虑网络外部环境的特性，对其原子服务进行科学有效定价。文献[6]在对移动网络数据定价和调度资源进行研究时指出，网络中一些合成服务的存在会影响网路的整体定价和稳定等。但是当前的研究并没有提出指导网络服务提供商针对合成服务进行科学有效定价的模型和策略。本文基于网络服务的经济特性，研究网络服务提供商对合成服务的定价模型，从而指导网络服务提供者合理地定价和优化网络合成服务。然而，网络合成服务的定价作为一种经济行为，准确构建其模型存在诸多挑战甚至可能难以实现。

网络服务定价关乎着网络服务的普及和提供商的经济收益，因而这方面的研究在商业界和学术界获得了广泛关注。根据这些研究可知，影响网络服务定价的因素有服务质量、服务成本、交易量以及竞争。其中，服务质量在影响消费者选择的因素中经常占据更重要、更优先的位置；服务成本表示与提供的服务相关的成本；交易量包括提供者和请求者交易的次数、交易的机构基础设施等；竞争能够驱动服务提供者为提高利润而做出最佳的反应[7]。

对于网络服务定价问题，前人有相关的研究基础。例如，文献[8]提出网络服务定价结构，在该结构中，合成服务中的网络服务能够适当地交流，并且提出了在零效果、零报酬系统中递增计算价格的定价机制。文献[9]通过做网络试验，研究了在服务组合市场中的定价问题，挖掘可能影响定价模型的因素。文献[10]提出了不同种类的定价模型，即固定费用模型、动态费用模型和混合费用模型。(1)固定费用模型即服务消费者需要支付给服务提供者固定的费用，从而获得某种服务。(2)动态费用模型即消费者支付的费用依赖于其实际使用的服务。(3)混合费用模型即被认为是固定费用模型和动态费用模型的结合，能够给服务消费者提供更多的灵活性。

本文采用固定费用定价模型，即服务提供者必须在交易之前设定固定服务费用，交易之后，服务消费者可以在固定时间内或者永久调用服务。

本文将供应链管理中的定价模型应用于网络合成服务定价。在供应链管理中，每一个参与者(制造商、中间商、零售商)都需要制定将产品传送给其继任者的合理价格[11]。供应链的产品提供商为了最大化市场收益份额，总是存在价格竞争，而该竞争同样存在于网络服务市场。因而，可将供应链管理中的相关定价模型应用于网络服务市场。同时，本文提出的网络合成服务定价模型，可以为服务提供商的决策提供支持。

1 网络合成服务定价

1.1 问题背景

图1的例子被用来说明网络合成服务定价的特点[12]。

图1 网络合成服务实例Fig.1 Sample of network synthesis service

有3个任务(A，B和C)需要建立网络软件并提供汽车保险服务。A和B有着相同的工作流，即通过Car Search，Car Selection和Insurance Offer提供汽车保险服务；C通过People Search和Insurance Offer提供汽车保险。其中：A、B、C表示不同的任务；1， 2， …， 6分别表示网络中不同的组件服务。由于1、 2、 4是单独的服务，因而其属于该网络中的原子服务。在该网络合成服务中，原子服务1、 2、 4通过组合，形成了网络中的组件服务3、 5、 6。而原子服务和组件服务之间的相互组合，形成了网络中的组合服务。如1-3-5(从1到3再到5的整个服务组合)是一个组合服务。一个组合服务构成了网络合成服务中的独立任务。如任务A是由组合服务1-3-5构成；任务B是由组合服务2-3-6构成；任务C是由组合服务4-6构成。

A，B和C通过组合在工作流中提供组件服务并分别独立构建网络合成服务，如：1-3-5构成A。由于组件服务3和6由不同的网络合成服务构建，因而一个网络合成服务结构可以通过结合A、B、C合成服务构成。网络合成服务可以被看作是多任务、多合成服务和多组件服务的结合。

从软件功能选择者的角度，他们可能并不关注网络合成服务的具体结构，更多的是关注选择的结果。对于服务提供商，当他们在注册中心中发布和更新服务时，需要给出相应的交易价格。在网络合成服务的供应链中，对服务的定价受以下2种情况约束：(1)定价过高导致服务消费者选择竞争对手；(2)定价过低尽管能带来高需求，但产生的利润很少。

1.2 假设

1.2.1 价格和服务透明性

价格和服务透明性是指市场参与者知晓商品和服务的普遍性价格和特征的程度[13]。事实上，在电子市场中，SOA架构和Web 2.0的发展促使服务提供商在特定领域提供产品和交易信息，因而领域内的相关价格和服务信息均被透明[14]。价格和服务透明性有2种方式使电子市场受益：(1)巨大的市场透明性可以加重服务提供商之间的价格竞争[15]；(2)价格竞争将促使服务提供商提高服务质量。

随着电子市场存在的服务越来越多，服务提供商之间对于服务的价格和质量竞争越来越激烈，电子市场逐渐变成买方市场。相关研究指出，为了吸引更多的买家，在存在价格和服务透明性的前提下，成功的电子市场必须为服务提供商提供相应的补偿[16]。

1.2.2 利润和需求

为评价定价策略，服务提供商需要了解或评价获得的利润以及服务消费者对他们的决策做出的反应。与其他固定成本相比，操作成本对于利润的影响可以忽略不计[17]。另外，被普遍使用的经济假设如下：

(1) 合成服务的价格越高，该合成服务的需求量越少；

(2) 实现一个特定任务的代价越高，本市场越小[18]；

(3) 网络服务市场存在服务需求变动。

为了直观地表达上述假设，本文用数学公式构建上面的假设。为了简化符号，i为任务的下标，j为网络合成服务下标，k为组件服务下标。对于第一个假设，假设第i个任务，其市场大小为Mi，有n个可用的合成服务共享市场Mi，用Gij代表第j个合成服务。对于Gij来说，其市场中份额为

(1)

式中：Pij为Gij的全部价格。由式(1)可得，价格越高，其市场占有份额越小。实现一个特定任务的平均价格(在下文中被定义为效用价格)为

(2)

根据假设(2)和(3)，第i个任务的市场需求量可以在时间跨度[t1，t2]范围确定，具体为

(3)

(4)

结合式(3)和(4)，市场大小可以表示为

(5)

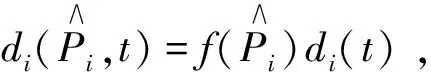
(6)

1.3 模型的目标

本文构建模型的目标是平衡服务提供商的效率和公平。为量化计算和简化说明，网络合成服务定价模型有如下所述目标准则。

1.3.1帕累托最优与均衡

为了平衡网络合成服务中的效率和公平，有两种解决方案可供选择：帕累托最优和纳什均衡。考虑到网络合成服务结构的技术和经济过程，本文选择帕累托最优方法平衡网络中的效率和公平，具体原因为：(1)对于大型网络，由于无法满足伸缩性，理论上无法保证最优定价[19]；(2)在网络服务市场，一些不合理的行为(如服务提供商提供免费服务[20])可能发生。

1.3.2 网络定价中的多目标与双目标

令Sk表示从网络合成服务中第k个服务提供商获得的利润。为了获得帕累托解，构建网络目标为

max(s1，s2， …，sn)

(7)

虽然式(7)可以保证网络中的公平和效率。但当网络中服务提供商数量超过4时，该多目标存在如下问题[21]：

(1) 当目标数量增加时，几乎所有的解决方案都不占优，这严重影响算法的收敛；

(2) 当目标数量很多时，接近帕累托前沿的解呈指数型增长。

现实中的网络合成服务结构，服务提供商的数量通常超过4个。为了克服采用帕累托最优方法解决问题的困难，本文将多目标转化为双目标。对于第k个服务提供商，双目标表达为

(8)

式(8)表示每个服务提供商在优化自己利润的同时，需考虑网络整体的收益。

1.4 问题建模

本文问题的模型由6个部分组成：组件服务、任务、合成服务网络结构、任务图、合成服务和目标。

任务。网络中有r个任务{T1，T2， …，Tr}，完成每个任务需要组合多个组件服务。每个任务在[t1，t2]区间内的市场大小可以通过式(5)获得。本文用Gi=(Vi，Ei)表示完成任务Ti的图模型，其中，Vi⊆V；Ei，表示完成任务Ti的边集。

合成服务网络结构。合成服务网络结构可由[t1，t2]时间内的所有任务的图模型构成，可表示为G=(V，E)。

合成服务。每个任务可由多个合成服务组成。对于任务Ti，第j个可行解决方案可被表示成：Gij= (Vij，Eij)，其中，Vij⊆Vi代表组件服务集合；Eij⊆Ei表示服务执行序列。每一个Gij的价格Pij是包含在组件服务集合内的全部组件的价格。每一个Gij占有的市场大小Dij可由式(1)获得。

目标。由于操作成本可以忽略不计，每个组件服务k的全部收益可表示为

(9)

对于每个服务提供者k，其目标可由式(8)获得。

1.5 复杂度分析

网络合成服务定价问题的复杂度，可以通过证明式(10)单目标问题的复杂度得到。

(10)

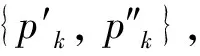
证明对于合成服务网络定价模型，构造子集合求和问题为

(11)

(12)

因为

(13)

由式(13)减式(12)可得到

(14)

结合式(2)，则效用价格为

(15)

通常情况下，多目标优化问题比单目标优化问题更加复杂[23]。因此，通过上述计算可以证明本文的网络合成服务定价问题至少是NP完全问题。

2 仿真试验

为了进一步量化并对比本文提出的网络合成服务定价模型给网络经济中的服务提供商带来优化决策的建议，本文设计了相应的仿真试验。

2.1 试验设计

仿真试验主要是用来仿真本文提出的模型并验证其优越性。本文将供应链管理中的相关理论知识应用于网络合成服务，能定量化地辅助网络服务提供商进行相关网络服务的定价。为了优化对比试验的仿真结果，本文假设市场上共提供15种不同的网络合成服务，共同组成市场上10种不同的客户任务，其相应的任务市场需求大小由仿真试验随机产生。最终对比验证本文的假设和提出来的模型的优越性，以及辅助网络合成服务提供商对相应的任务制定合理的价格，从而能够平衡网络服务市场的效率和公平。

2.2 试验数据

为了定量化地验证本文提出的模型在指导服务提供商定价上的优越性，随机产生如下的客户任务需求量。市场上分布的10种不同客户的任务量大小如表1所示。

表1 市场上10个任务的需求量Table 1 Demand of ten-market tasks 个

为简化试验计算过程，仿真试验假设市场上有15个合成服务共享市场M。为了量化地验证试验结果，随机产生的服务商定价表如表2所示。

表2 客户定价表Table 2 Table of customer price 元

从表2中可以详细获得各个供应商对应的不同服务的定价。对于同一个服务，不同供应商的定价基本不同，这可能跟供应商提供服务的质量和成本等因素有关。对于同一个供应商，其对不同服务的定价也基本不同，这可能跟不同服务本身存在的不同特点有关。因而可以得到，供应商会根据提供服务的不同和提供服务的成本等因素，进行差异化定价。

2.3 结果分析

通过式(1)的计算可得到客户市场份额分布如表3所示。

表3 客户市场份额分布Table 3 Marketshare distribution of customers

从表3可以看出，不同供应商对不同服务的占有量往往不同。结合表2和3相对应的内容，可以挖掘供应商对不同服务的定价和市场占有量之间的关系，如图2所示。

图2以表2和3的前6个网络服务作为例子，分析供应商对不同服务的定价和所对应的市场占有量之间的关系。从图2中的曲线变化关系可以看出，一般情况下，供应商对某一服务的定价提高，其所对应服务的市场占有率往往会降低。但是仍然存在一些特殊情况，从图2中的线条ABC、DE等可以看出，对于某些特定的服务，即使在一定程度范围内提高定价，其市场占有率仍然不变或者会升高。对于网络服务提供商而言，明确服务定价和市场占有量之间的关系，能够有效地指导服务提供商对特定服务进行科学有效定价。因而，为了挖掘出这一定量的关系，本文做了下文的灵敏度分析。

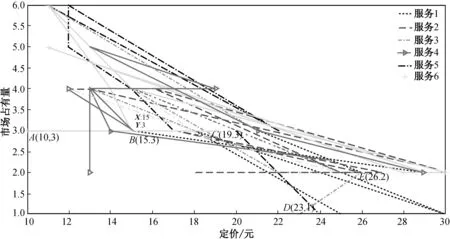
图2 前6个服务的定价与市场占有量关系图Fig.2 Relation between price and market share at the first six services

2.4 灵敏度分析

通过模型推理和仿真试验验证可得到，在网络合成服务市场中，随着服务提供商对特定服务的定价提高，其市场份额会变小。这意味着，实现特定任务的不同的合成服务的代价越高，其市场占有量越少。为了进一步地分析供应商所提供的服务对所制定的价格策略的敏感性，本文分析了合成服务市场占有量变化对其市场价格变动的灵敏度。具体的灵敏度分析过程是用合成服务需求变动量除以其变动的价格，得出需求变动量对应的价格变动敏感性，如式(16)～(19)所示。

(16)

(17)

由式(16)和(17)可得

(18)

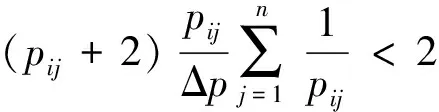
(19)

综上所述可知：当pij<2Δp时，Dij与pij同方向变化；反之，二者反方向变化。从灵敏度分析的结果可以看出，在其他各种因素不变的情况下，当供应商对其所提供合成服务的价格调整幅度超过原始价格的一半时，其所提供的合成服务的市场占有量会随着价格增大而增大。当供应商对其所提供的网络合成服务的价格调整幅度没有超过原来价格的一半时，市场占有量会随着价格的升高而减少。由此说明，供应商提供的合成服务的市场需求变化，在一定的价格波动内满足一般的市场需求价格变动理论[24]，但是当这种价格波动超过一定的范围，则不满足这种理论。因而，供应商在调整其提供的网络合成服务的价格时，需要根据这一结论进行相应的调整。

3 结 语

本文研究了竞争情况下网络合成服务定价模型，此模型作为一种仿真模型，可以给网络服务提供商提供相关决策支持。通过证明目标模型是NP完全问题，证明该问题获得帕累托最优解的困难性。通过灵敏度分析，可以得出在网络服务提供商面对不同的市场环境时，不同的定价往往能够带来不同的利润。当供应商对其所提供的合成服务的价格调整幅度超过当前市场价格的一半时，其所提供的合成服务的市场占有量会随着价格增大而增大，而当价格调整没有超过当前价格的一半时，市场占有量会随着价格的升高而减少。因而，对于不同的服务，网络服务提供商需要根据这一规律进行相应的差异化定价，从而给自己带来最大收益。