SELF-ADAPTIVE SLIDING MODE SYNCHRONIZATION OF A CLASS OF UNCERTAIN FRACTIONAL-ORDER VICTOR-CARMEN SYSTEMS
MAO Bei-xing,WANG Dong-xiao,CHENG Chun-rui
(College of Science,Zhengzhou University of Aeronautics,Zhengzhou 450015,China)
Abstract:In this paper,we investigate the sliding mode synchronization problem of fractional-order uncertain Victor-Carmen systems.By using self-adaptive sliding mode control approach,sufficient conditions on sliding mode synchronization are provided for the fractional-order systems,which verifies that the master-slave systems of fractional-order Victor-Carmen systems are sliding mode synchronization by choosing proper sliding mode surface and controllers.
Keywords:uncertain fractional-order;Victor-Carmen systems;siding mode;self-adaptive
1 Introduction
Recently,the chaos synchronization of fractional-order systems gained a lot of attention,such as[1–11].Sun in[12]addressed the sliding mode synchronization problem of fractional-order uncertainty systems,which the master-slave systems can realize project synchronization.The authors in[13]studied the problem of self-adaptive sliding mode synchronization of a class of fractional-order chaos systems,which the drive-response systems achieved chaos synchronization.Chaos synchronization control problem was investigated for fractional-order systems in[14].Zhang in[15]considered the self-adaptive trace project synchronization problem of the fractional-order Rayleigh-Duffing-like systems.Since the Victor-Carmen chaos systems involving lots of secreted key parameters and getting extensive use in communications,some results on this topic were investigated.For example,a novel chaotic systems was studied for random pulse generation in[16],and in[17],the terminal sliding mode chaos control of fractional-order systems was studied.In this paper,the problem of sliding mode synchronization of a class of fractional-order uncertain Victor-Carmen systems is tackled using self-adaptive sliding mode control approach,and sufficient conditions on sliding mode synchronization are derived for the fractional-order systems.
Definition 1.1(see[18])The fractional derivative of Caputo is given as follows
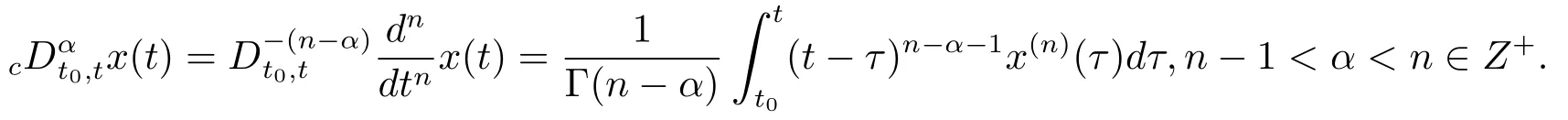
2 Main Results
Consider the following integer-order Victor-Carmen systems
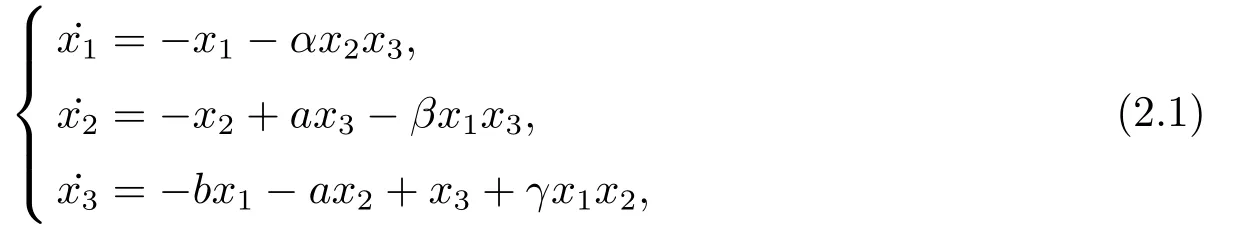
wherex1,x2,x3∈R3are system states,a,b,α,β,γare constant parameters.
The responsive systems are as follows
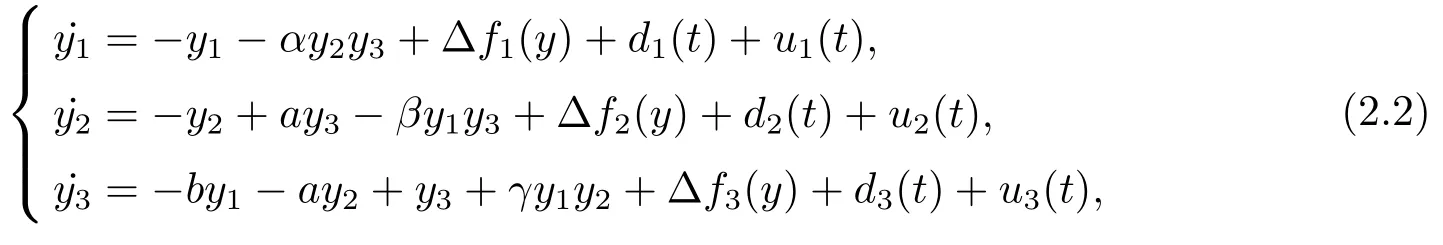
where∆fi(y)is uncertain,di(t)is bounded disturbance,uiis controller,subtracting(2.2)to(2.1),we get
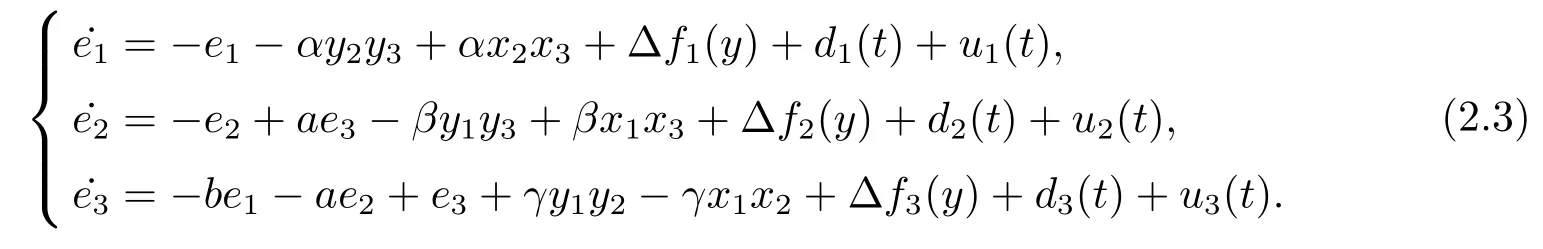
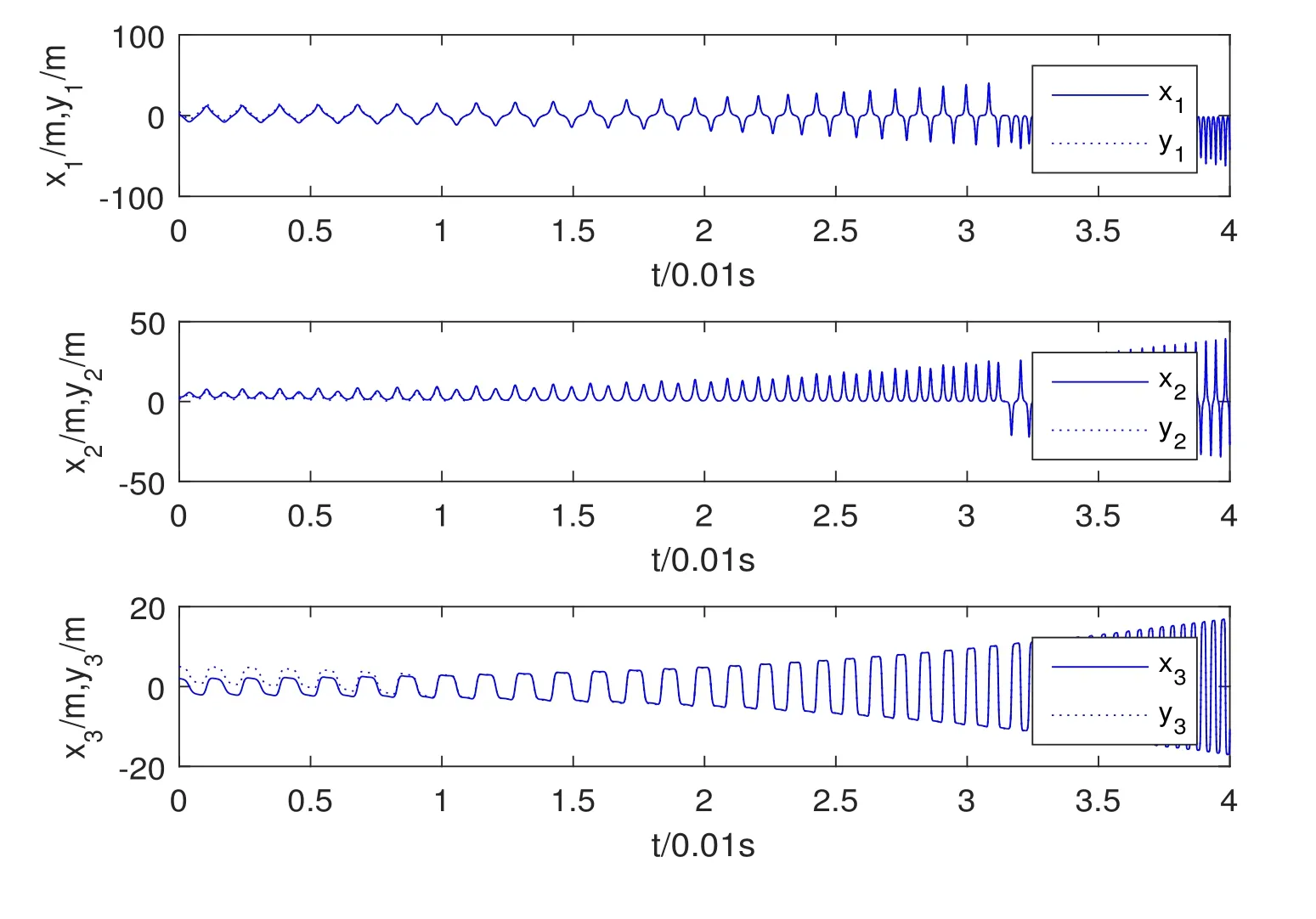
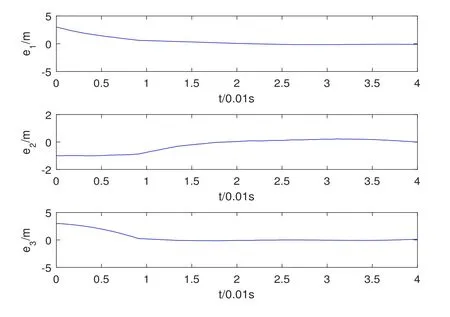
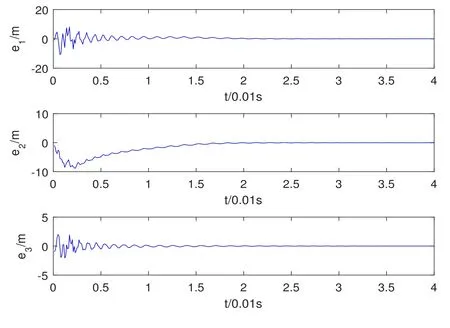
Assumption 2.1∆fi(y)anddi(t)are bounded,mi,ni>0,|∆fi(y)| Assumption 2.2miandniare unknown for alli=1,2,3. Assumption 2.3Definite∆fi(y)+di(t)=gi(t),i=1,2,3. Assumption 2.4gi(t)satisfies the condition|gi(t)|≤ε|ei(t)|,where 0<ε<1. Assumption 2.5Ifei(t)=0,thengi(t)=0 and ifei(t)6=0,thengi(t)6=0. Lemma 2.6(Barbalat’s lemma,see[19])Iff(t)is uniform continuity in[0,+∞),andis exist,then. Lemma 2.7(see[19])If there exists a symmetric and positive-definite matrix P such that,where the systems order number 0<α≤1,then general fractional-order autonomous systemsis asymptotic stable. Theorem 2.8Under Assumptions 2.1–2.5,choosing sliding mode functions(t)=e1+e2+e3,and the following controllers whereη>0,are the estimate values ofmiandni,and for alli=1,2,3,designing self-adaptive laws Then the master-slave systems(2.1)and(2.2)of integer-order Victor-Carmen systems are self-adaptive sliding mode synchronization. ProofWhen the systems state moving on the sliding mode surface,then we can gets(t)=0,(t)=0,because If we substitute(2.4)to(2.3),thensgn(s),i=1,2 fors(t)=0,it is easy to get.On the other hand,forsgn(s)−ηsgn(s),from(2.5),it is easy to gete1+e2=−e3,so we get,,i=1,2,3.According to Lyapunov stability theory,when,found Lyapunov function,we get When the systems aren’t moving on the sliding mode surface,we found Lyapunov function as,so it has sos(t)is bounded and integrable.From Lemma 2.6,we gets(t)→0⇒ei(t)→0,so the errors converge to zero. Consider the master systems of fractional-order Victor-Carmen systems Design the slave systems as following where∆fi(y)is uncertainty,y=[y1y2y3],di(t)is bounded disturbance,uiis controller,subtract(2.7)to(2.6),we get the following errors equation Theorem2.9Under Assumptions 2.1–2.5,design sliding mode function,choosing controller whereη>0,are the estimate values ofmi,ni,design self-adaptive laws Then the master-slave systems(2.6)and(2.7)of fractional-order Victor-Carmen systems are self-adaptive sliding mode synchronization. ProofWhen the systems state moving on the sliding mode surface,s(t)=0,s˙(t)=0,then,so we get,such that we have Substitute controller(2.9)to(2.8),we get,i=1,2,when the systems state moving on the sliding mode surfaces(t)=0,so it is easy to get According to Lemma 2.7,the solution of following equation,soei(t)→0,i=1,2,3.When the systems state moving on the sliding mode surfaces(t)=0,then the solution of errors equation(2.8)is asymptotic stable such that we getei(t)→0,i=1,2,3. When the systems aren’t moving on the sliding mode surface,we found Lyapunov functionsuch that we get According to Lemma 2.6,s(t)→0,so we getei(t)→0. In this section,the example is provided to verify the effectiveness of the proposed method.The systems appears chaos attractors,when the disturbance is bounded From Figure 1,we see that the systems aren’t getting synchronization without controller.From Figure 2,we see the systems getting rapidly synchronization with controller.From Figure 3,we see that the errors approaching zero,which verifies the systems getting chaos synchronization rapidly. In Theorem 2.8,g1(t)=cos(2πy2)+0.2cost,g2(t)=0.5cos(2πy3)+0.6sint,g3(t)=0.3cos(2πy2)+cos3t,η=2.5.The uncertainty and outer disturbance as Theorem 2.9,η=3,q=0.873,the systems errors as Figure 4. In this paper,we study the self-adaptive sliding mode synchronization problem of a class of fractional-order Victor-Carmen systems based on fractional-order calculus.The conclusion indicates that the systems are self-adaptive synchronization if designing appropriate controller and sliding mode function.We give out the strict proof in mathematics,and the numerical simulation demonstrates the effectiveness of the proposed method. Figure 2:State of master-slave with control Figure 3:The system errors of Theorem 2.8 Figure 4:The system errors of Theorem 2.9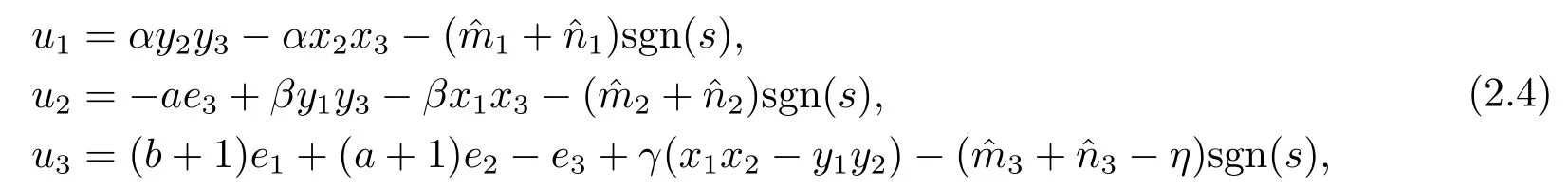
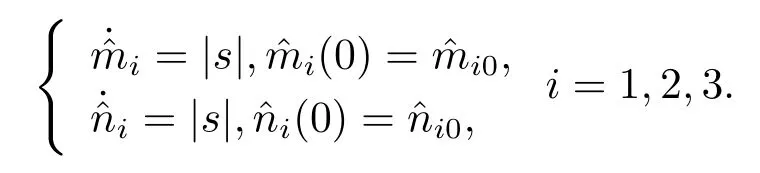

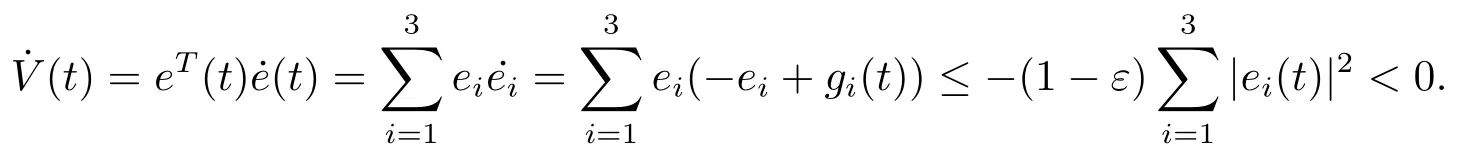
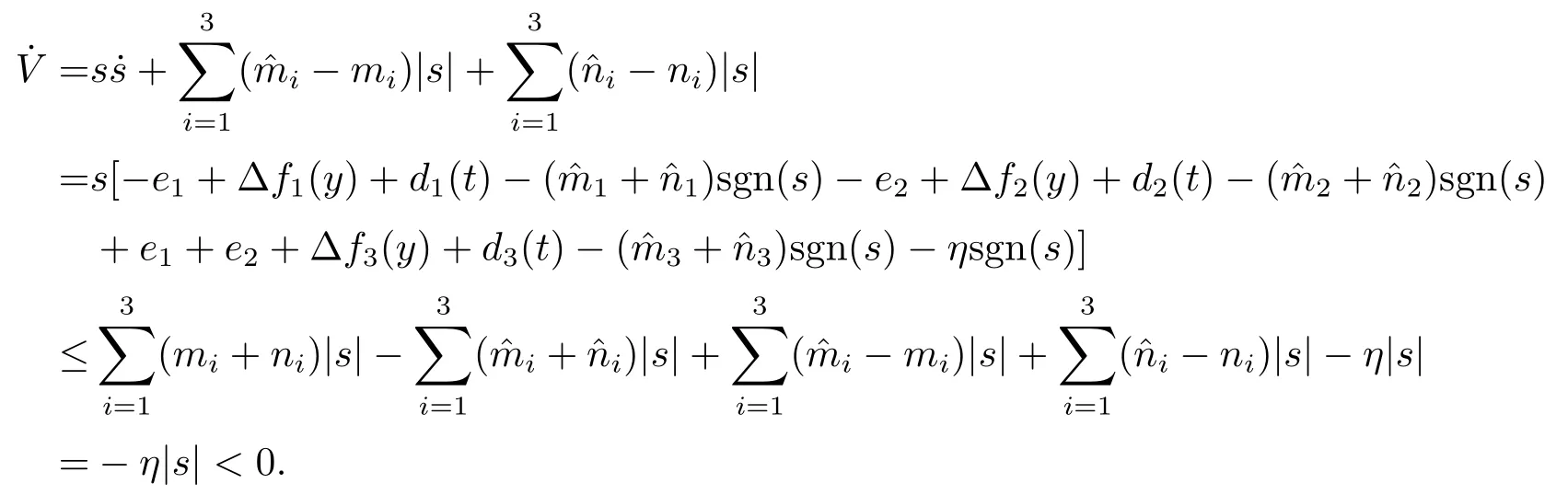
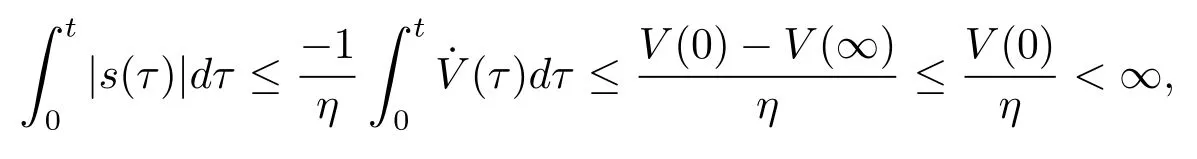
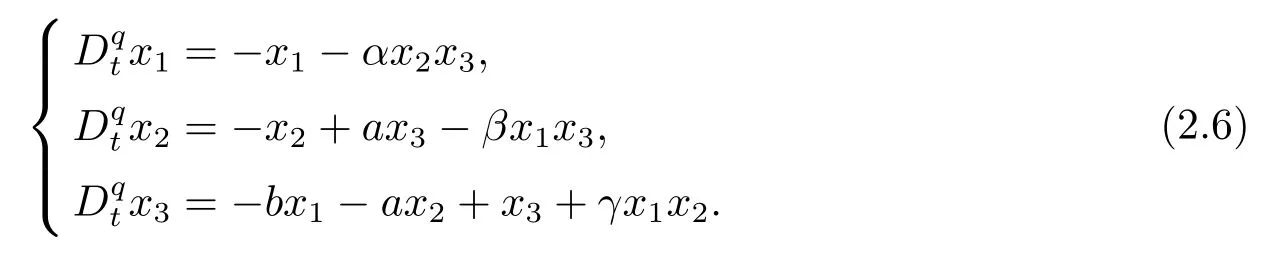
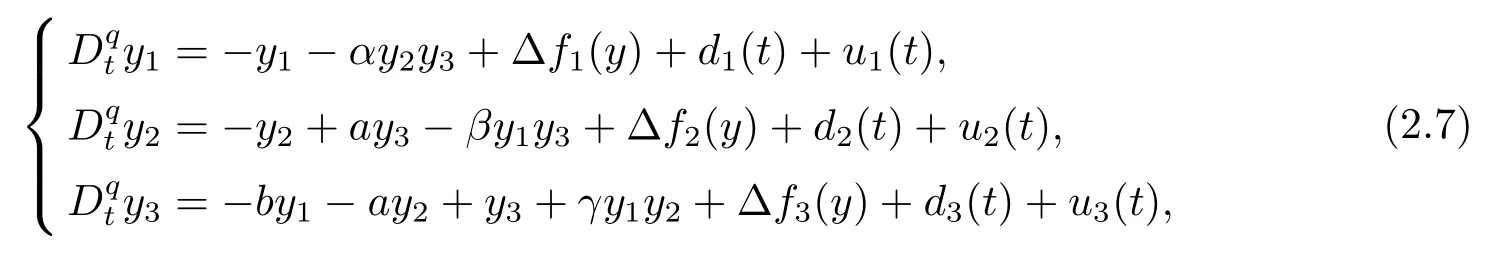
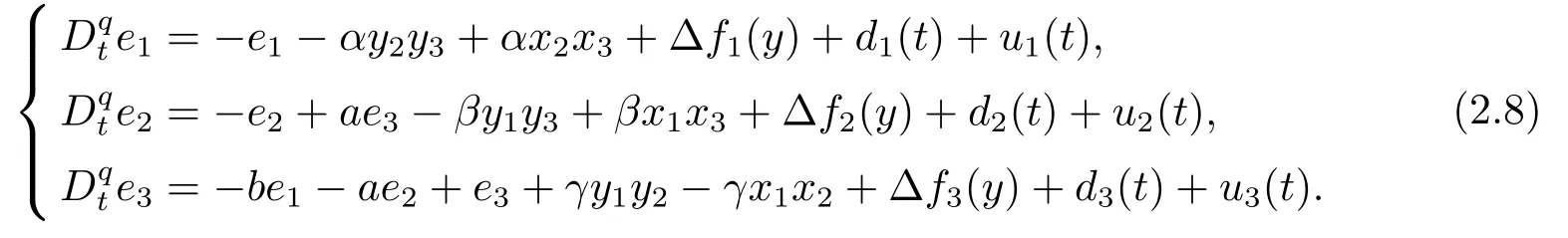
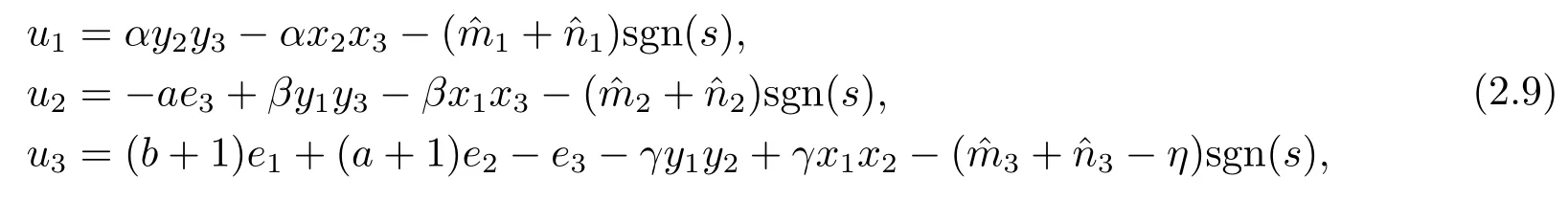
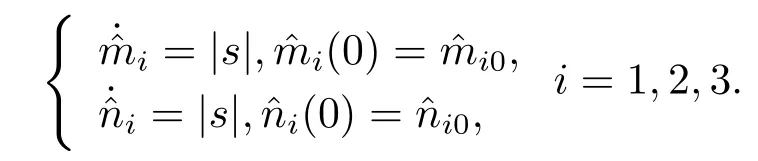

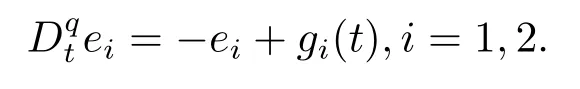
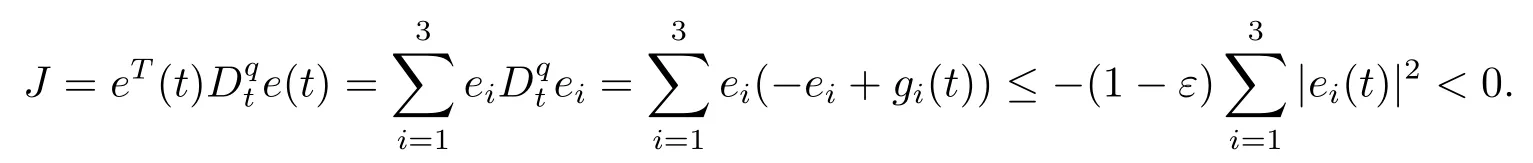
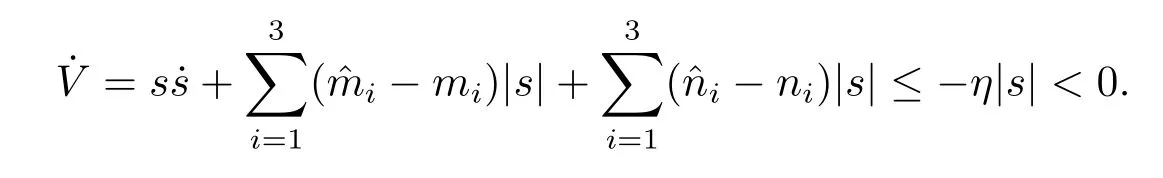
3 Numerical Simulation
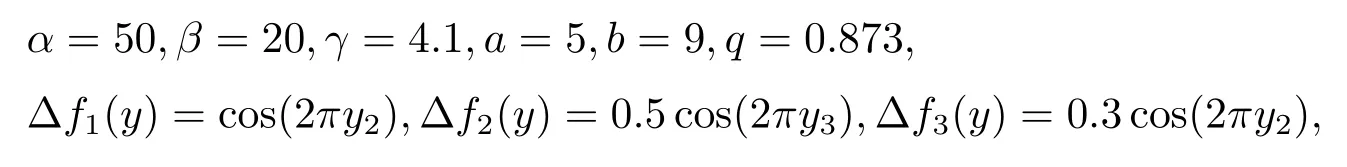
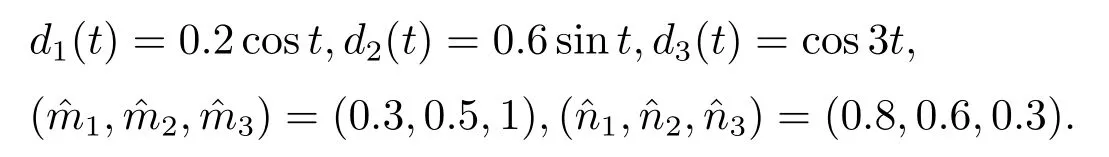
4 Conclusion